低轨大规模卫星星座内部防碰撞安全性分析
云朝明,胡敏,阮永井,薛文
1.中山大学,深圳 518107 2.航天工程大学,北京 101416
1 引言
随着航天技术和互联网技术的发展,世界航天大国先后提出了低轨互联网星座的概念,星座开始向低轨化、大规模化发展[1]。目前典型的低轨大规模星座计划有Starlink、OneWeb和Kuiper等,其中截至2022年8月21日,Starlink星座已累计发射3108颗卫星。
低轨大规模星座卫星数量巨大,发生一次解体碰撞会产生成百上千的空间碎片,这些碎片不仅会增加星座的碰撞概率,而且由于碎片面质比较小,在空间停留时间长,会对空间环境造成长期危害[2-6]。因此,无论从低轨大规模星座自身安全还是空间环境可持续性的角度出发,对低轨大规模星座轨道安全尤其是碰撞安全的研究是必要且亟需进行的[7-11]。
Virgili等引入大型星座来分析低轨道巨型星座部署对空间碎片碰撞概率的影响[12]。Le May等使用MASTER-2009碎片演化模型模拟了OneWeb和Starlink星座,并进一步分析了对星座参数的影响以及未能执行离轨操作的卫星的长期影响[13]。Foreman等研究表明,如果低轨大规模星座离轨处置执行不当或根本不执行,使得航天器不能完全离轨或置于安全的墓地轨道,损坏的航天器会增加低地球轨道上其他航天器的碰撞风险[14]。Pardini等提出了“体积碰撞率指数”作为指标,用于评估意外碰撞导致低轨空间内完整物体完全破坏的可能性,并应用于低轨大规模星座部署后的环境评估[15]。这些研究主要围绕任务后处置对空间环境的影响,以及空间碎片与卫星星座的相互影响,但没有涉及星座内部的安全性。
低轨大规模星座内部卫星数量庞大,采用一箭多星的发射方式进行组网。在星座组网运行时,不仅需要考虑星座与外部空间环境的相互影响,还需注意星座的内部安全。刘广军等提出了一种判断星座中卫星发生碰撞的预测方法[16]。该方法通过碰撞预测,可以评估为了避免碰撞而进行的轨道机动,并确定在给定的星座中不能放置卫星的位置。文献[17]研究了星座卫星之间的“自诱导”会合以及碰撞预测方法的可靠性。针对Walker星座的碰撞问题,国内学者进行了深入研究,吴启星等设计了一种Walker星座碰撞检测模型[18];王春明等分析了Walker星座卫星的几个常量参数,推导了轨道交点的卫星角距计算公式和碰撞判决公式,得到了快速计算星座最小卫星间距的方法[19]。
星座内部的安全性需要关注入轨分离时的碰撞风险、正常工作时的异轨卫星间的碰撞风险。大规模星座在初始设计状态下,其星座构型具有一定的安全性,但是星座卫星在初始化或进行轨道控制时存在控制偏差,造成卫星的实际位置与标称位置出现偏差。由于各个卫星的偏差存在差异,在摄动力的作用下,星座卫星间会发生相对漂移,导致卫星偏离理论相位。当漂移量达到一定程度时,就可能在交会处与其他轨道平面卫星发生碰撞。为了避免星座卫星间的碰撞,必须保证星座空间几何构型维持在一定关系范围内,需要约束卫星沿升交点赤经(right ascension of ascending node,RAAN)和相位的漂移量,这个约束的阈值被称为星座构型最大容许漂移量。
本文通过对星座构型最大漂移量进行研究来分析星座卫星间的安全性。在计算得到卫星轨道平面最小相位差的基础上,分析构型参数和升交点赤经漂移量对最小相位差的影响,并提出基于最小相位差的星座构型参数协同设计方法,最后以Starlink第一期星座为参考进行仿真,验证了该方法的合理性。
2 低轨大规模星座最小相位差计算
星座最小相位差是星座卫星在穿越其他轨道面时与该轨道平面内最接近卫星的相位差。星座卫星之间的碰撞是由于星座卫星初始偏差不同,在摄动力的作用下,卫星之间产生相对漂移,并在长期的积累下,卫星之间不断接近导致的。卫星在接近速度相同的情况下,具有最小相位差的两卫星之间发生碰撞的时间短。为保证星座构型安全,要求星座内相对相位最小的两卫星不发生碰撞,则可求解星座卫星的最小相位差,以最小相位差作为漂移约束,求解星座构型最大漂移量。
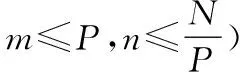
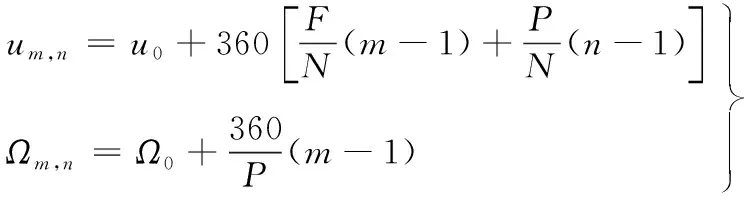
(1)
式中:u0为第一轨道面第一颗卫星的相位;um,n为t0时刻卫星(m,n)的相位;Ωm,n为t0时刻卫星(m,n)的升交点赤经。如图1所示,星座任意的两轨道平面,当某一轨道平面卫星跨越另一轨道平面时,由于星座内各卫星相对位置确定,跨越另一轨道平面的卫星与该轨道面最接近的卫星的相位为最小相位。因此,对任意两轨道平面,卫星间的最小相位是确定的,可以通过某卫星跨越不同轨道平面时与该轨道平面的最小相位差求解整个星座的最小相位差。
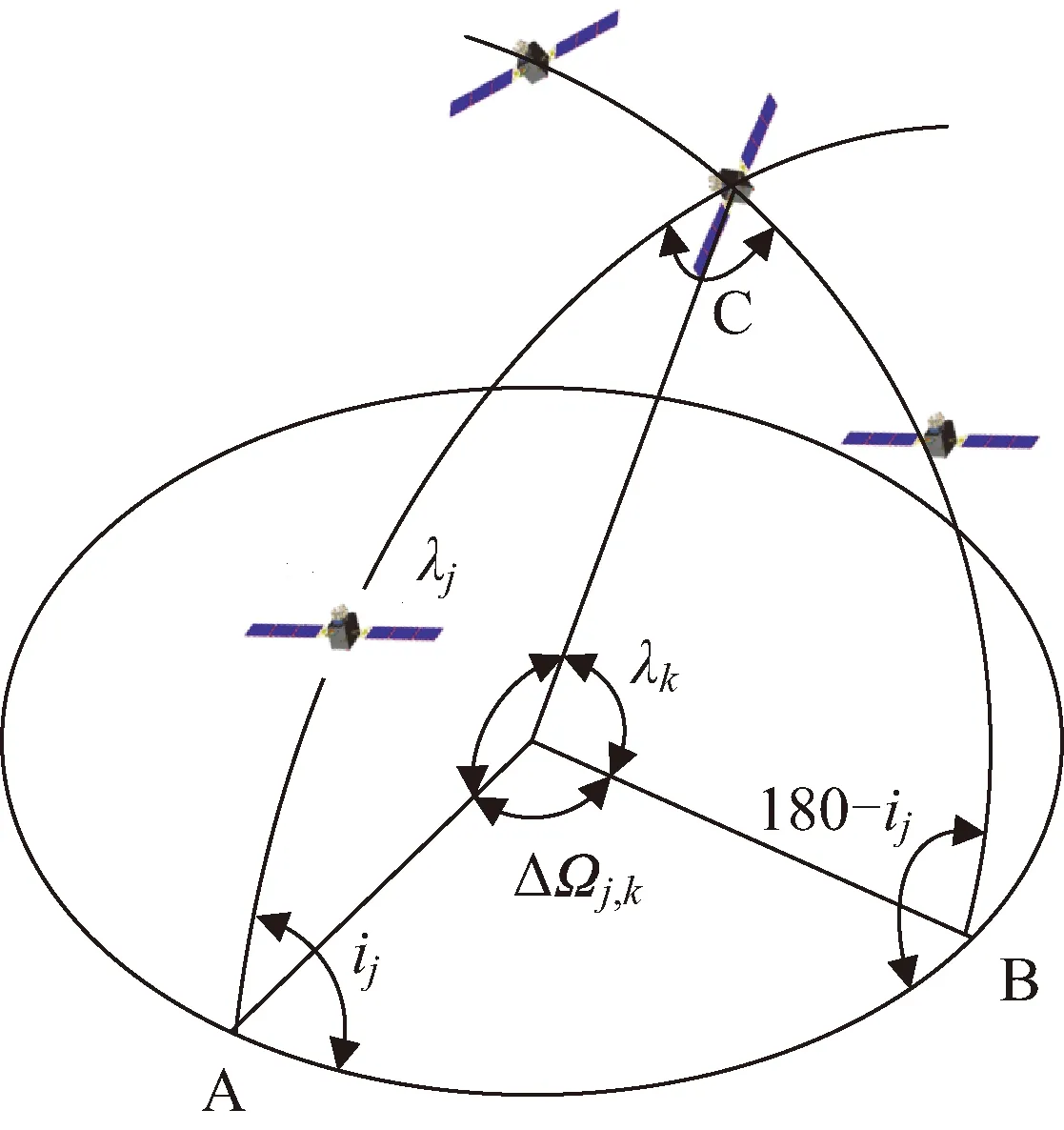
图1 卫星交会示意Fig.1 Schematic diagram of satellite rendezvous
为了求解卫星在跨越另一轨道平面时卫星之间的相对相位,需先求解两轨道平面交点在各自轨道平面内的相位。在轨道倾角和两轨道面升交点赤经差已知的情况下,可以通过球面三角形角的余弦定理求解出楔角C,再利用球面三角形边的余弦定理求解出两轨道面交点在两轨道平面内的相位。轨道平面交会几何图如图1所示,根据两轨道平面之间升交点赤经差值分两种情况讨论,当轨道平面j与轨道平面k的升交点赤经差ΔΩj,k<180°时,根据球面三角形余弦定理可得轨道平面j和轨道平面k之间的楔角C为:
C=arccos(-cosicos(180°-i)+
sinisin(180°-i)cosΔΩj,k)
(2)
式中:i为轨道倾角。得到轨道平面j与轨道平面k的交点在轨道平面j内的相位λj为:
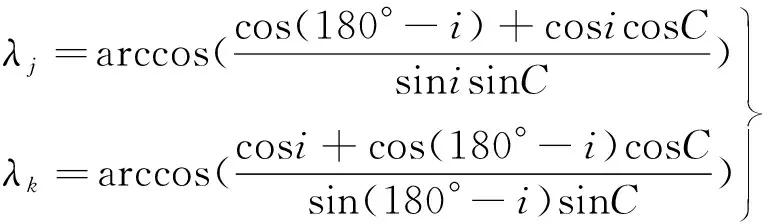
(3)
当ΔΩj,k≥180°时,得轨道平面j和轨道平面k之间的楔角C为:
C=arccos(-cosicos(180°-i))+
sinisin(180°-i)cosΔΩj,k
(4)
得到轨道平面j与轨道平面k的交点在轨道平面j内的相位λj为:
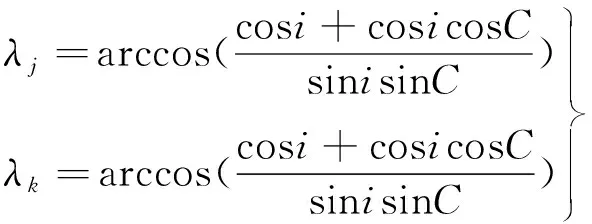
(5)
令轨道平面j中第一颗卫星j1为基准卫星,当卫星j1穿越轨道平面k时,根据公式(1)可得轨道平面k中第一颗卫星k1的相位:
(6)
由于轨道平面内卫星间间距相等,在同一轨道平面内的卫星相位差与卫星间距成整数倍,当知道两卫星间的相位差时,对相位差与卫星间距求商即可求得跨越卫星处于相邻卫星间的位置情况。
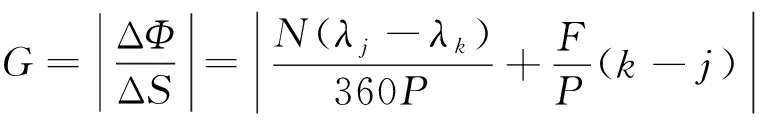
(7)
式中:G为穿越卫星在相邻平面中的位置;ΔΦ为j1与k1相位差;ΔS为卫星间间距。可以得到卫星j1与轨道平面k的最小相位差为:
dφj1,k=min(ceil(G)-G,G-fix(G))
(8)
式中:dφj1,k表示第j轨道面第一颗卫星与第k轨道面间的最小相位差。由于两轨道平面卫星分布相同,轨道面内卫星间相位相等,对j平面内任意卫星都存在当卫星穿越轨道面k时,与轨道平面k内卫星间相位差相等。因此,轨道面j和轨道面k之间的最小相位差φj,k为:
φj,k=dφj1,k
(9)
两轨道面间最小相位差为φj,k,则低轨大规模星座卫星间的最小相位差φc为:
φc=min(φj,k)
(10)
式中:j=1,2,…,P-1;k=j+1,…,P。
3 星座构型参数对轨道平面最小相位差的影响
低轨大规模星座轨道平面最小相位差与星座结构参数、轨道倾角和轨道平面升交点赤经差相关,而星座最小相位差决定了低轨大规模星座相位漂移量的大小。轨道平面间最小相位差越大,相位能够漂移的角度越大。由于轨道平面间的夹角不连续,造成不同轨道平面之间卫星最小相位差值不连续,不能建立星座构型漂移量与星座构型参数的函数关系。因此,本文通过研究星座构型参数与轨道平面最小相位差的关系,使卫星间最小相位差值尽可能大,从而研究星座构型参数对星座最大漂移量的影响。
3.1 星座构型参数对相邻轨道平面最小相位差的影响
星座结构参数N/P/F、轨道倾角i、轨道高度h是描述Walker星座构型的参数,其中N/P/F相互制约,N的取值影响P的取值范围,F是0~(P-1)之间的一个整数。不同的构型参数可以组成许多种不同形状的星座,相邻轨道平面最小相位差也不相同,因此,本文采用控制变量法研究卫星数量、轨道面数量、相位因子和轨道倾角对相邻轨道平面最小相位差的影响。
根据卫星最小相位差定义可得,卫星最小相位差为穿越异面轨道时与其他轨道面最接近卫星的相位差,由于轨道面内相邻卫星之间的相位差为360°P/N,得到卫星最小相位差取值范围为[0°,180°P/N]。
3.1.1 卫星数量对最小相位差的影响
根据卫星最小相位差取值范围可知,随着卫星数量不断增大,在轨道平面数量、相位因子和轨道倾角不变的情况下,星座相邻卫星间的相位差值范围会不断减小,导致参考平面与各轨道平面最小相位差的取值范围变小。令星座轨道倾角为60°,初始卫星数量N为300颗,轨道面数P为30,相位因子F=1,每次增加与轨道平面数量相同的卫星数进行仿真,得到星座在不同卫星总数下与相邻轨道平面最小相位差的关系如图2所示。
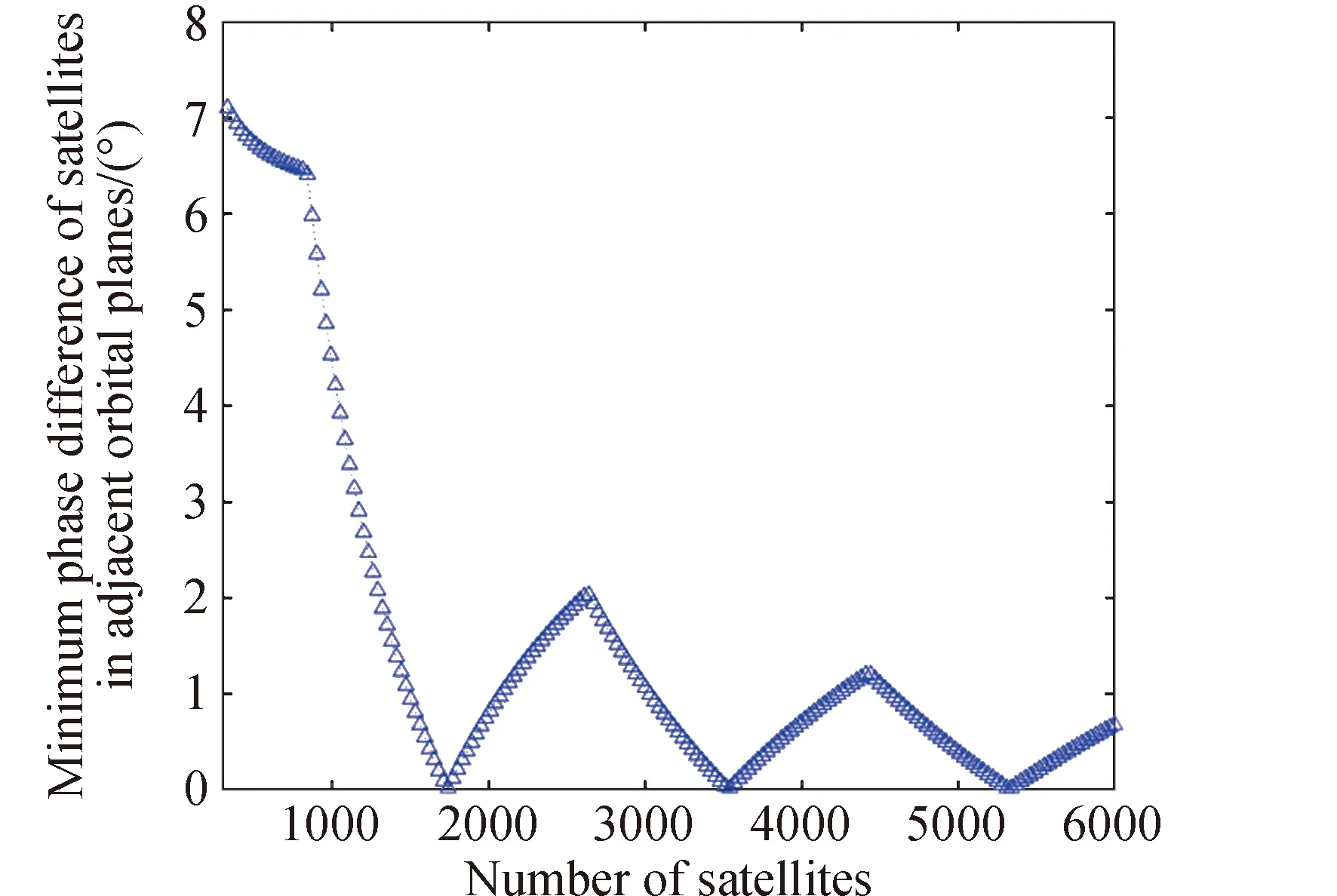
图2 星座卫星总数与相邻轨道平面最小相位差关系Fig.2 The relationship between minimum phase of constellation and the number of satellites
从图2可以看出,当轨道平面数量一定时,穿越卫星在穿越平面内与相邻两颗卫星的相对位置会随着星座卫星数量的变化而变化,当卫星数量小于900颗时,星座相邻轨道平面卫星最小相位差变化缓慢。而当卫星数量大于900颗时,可以看出星座相邻卫星的最小相位差,随卫星数量的变化呈现出振幅不断下降和周期变大的周期震荡。因此,本文以900颗卫星为分界线,研究900颗以上卫星组成的低轨大规模星座。
3.1.2 轨道面数量对最小相位差的影响
当卫星数量、相位因子和轨道倾角固定,仅轨道平面数量增加时,令星座轨道倾角为60°,卫星数量N为1200,相位因子F=1,仿真卫星轨道平面数量从3个逐渐到100个情况下星座的最小相位差,得到如图3所示的关系图。
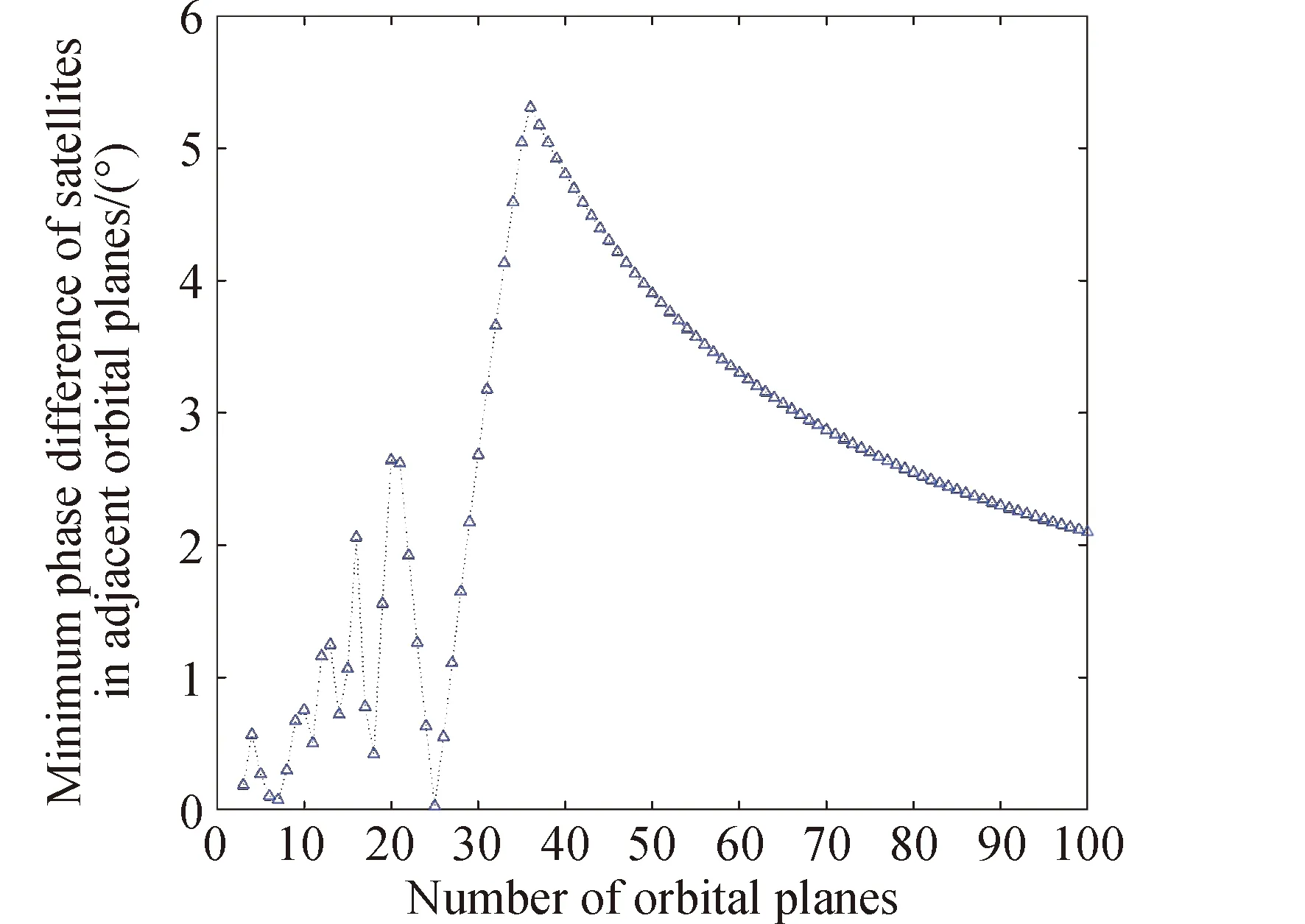
图3 轨道平面数与星座最小相位差关系Fig.3 The relationship between minimum phase of constellation and the number of orbital planes
从图3可以看出,随着轨道平面数量的增加,星座最小相位差由波动变大到逐渐趋于稳定下降。这是由于轨道平面较少时,星座最小相位差较小,升交点赤经差的变小导致相邻卫星间的相位变大,穿越卫星与穿越平面内相邻两颗卫星的最小相位差取值范围更大,因此会出现波动的情况。随着轨道平面数量增多,卫星之间升交点赤经越来越小,虽然星座最小相位差取值范围逐渐变大,但随着轨道面逐渐接近,穿越卫星位置会逐渐接近穿越平面内具有相同编号的卫星,即星座最小相位差的值会不断趋于Δu。
3.1.3 相位因子对最小相位差的影响
当卫星数量、轨道面个数及轨道倾角固定,仅相位因子变化时,令星座轨道倾角为60°,卫星数量N为1200,轨道面个数为60,仿真相位因子从1到59星座的最小相位差,得到如图4所示的关系图。
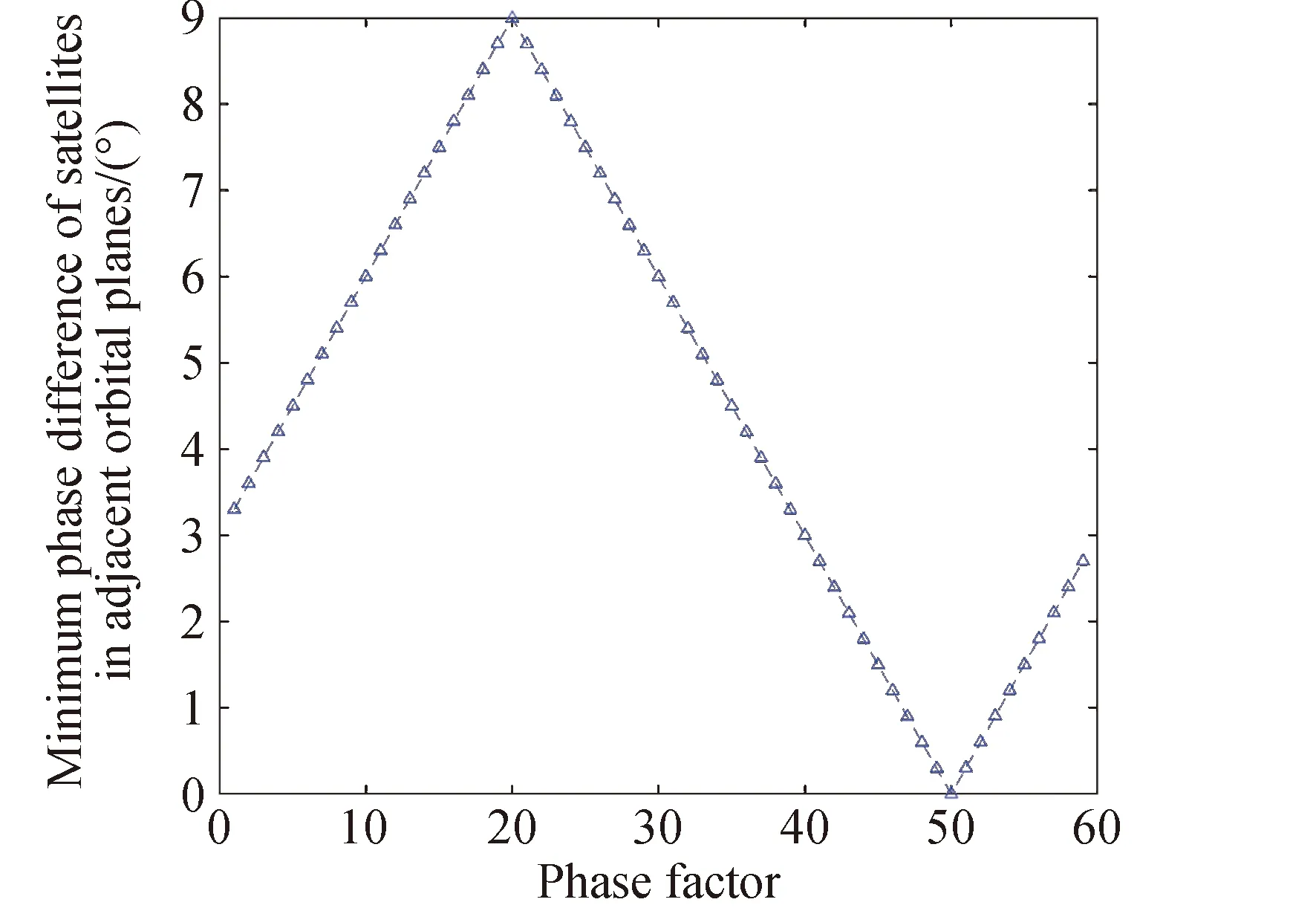
图4 相位因子与相邻轨道平面卫星最小相位差关系Fig.4 The relationship between phase factor and the minimum phase difference of adjacent orbit plane satellites
由于卫星数量和轨道面个数固定,可以得到星座最小相位差取值范围为[0°,9°],由图4可以看出,卫星最小相位差与相位因子在取值范围内呈线性周期变化,可以通过调节相位因子得到合适的最小相位差值。
3.1.4 轨道倾角
当低轨大规模星座结构参数固定,仅轨道倾角变化时,令卫星数量N为1200,轨道面个数为60,相位因子F=1,仿真轨道倾角从30°到89°星座的最小相位差,得到如图5所示的关系图。
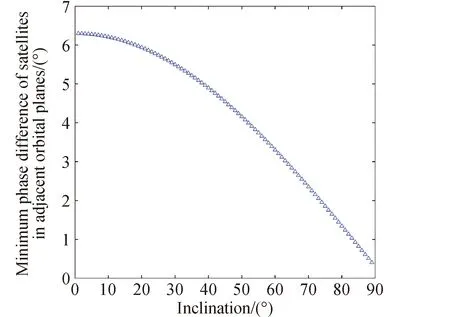
图5 轨道倾角与相邻轨道平面卫星最小相位差关系Fig.5 Relationship between inclination and minimum phase difference of satellite in adjacent orbital plane
由图5可知,相邻轨道平面卫星最小相位差随轨道倾角的增加单调递减。可以得到当低轨大规模星座结构参数固定时,星座最小相位差可以通过轨道倾角进行调节。
综上所述,低轨大规模星座结构参数中,卫星数量和卫星轨道平面数量既可以影响穿越卫星穿越平面内的位置,影响最小相位差的实际取值,还能影响最小相位差的最大取值范围;而相位因子和轨道倾角则只能调节穿越卫星穿越平面内的位置,影响最小相位差的实际取值。因此,星座最小相位差受到多重因素的影响,由于在通常情况下星座卫星数量和轨道平面数量都和星座性能参数相关,当星座卫星数量和轨道平面数量确定时,提出了基于最小相位差的星座构型参数协同设计方法,通过对相位因子和轨道倾角进行协同调节设计,调整星座的最小相位差,设计出较优的星座相位漂移量。
3.2 升交点赤经漂移量对轨道平面最小相位差的影响
星座构型参数一定的条件下,当星座两轨道平面确定时,轨道平面间最小相位差仅与星座轨道平面间的夹角有关。对于星座的标称轨道,由于轨道平面间的夹角不会发生变化,此时升交点赤经漂移量为0,星座相位角漂移量为星座所有轨道平面最小相位差的1/2。然而,在实际情况下,由于星座卫星存在控制偏差以及受到摄动力的影响,升交点赤经会发生漂移,造成两轨道平面升交点赤经差发生变化,导致轨道平面最小相位差改变,最终影响卫星相位漂移量。
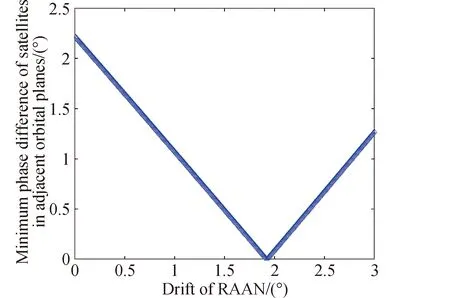
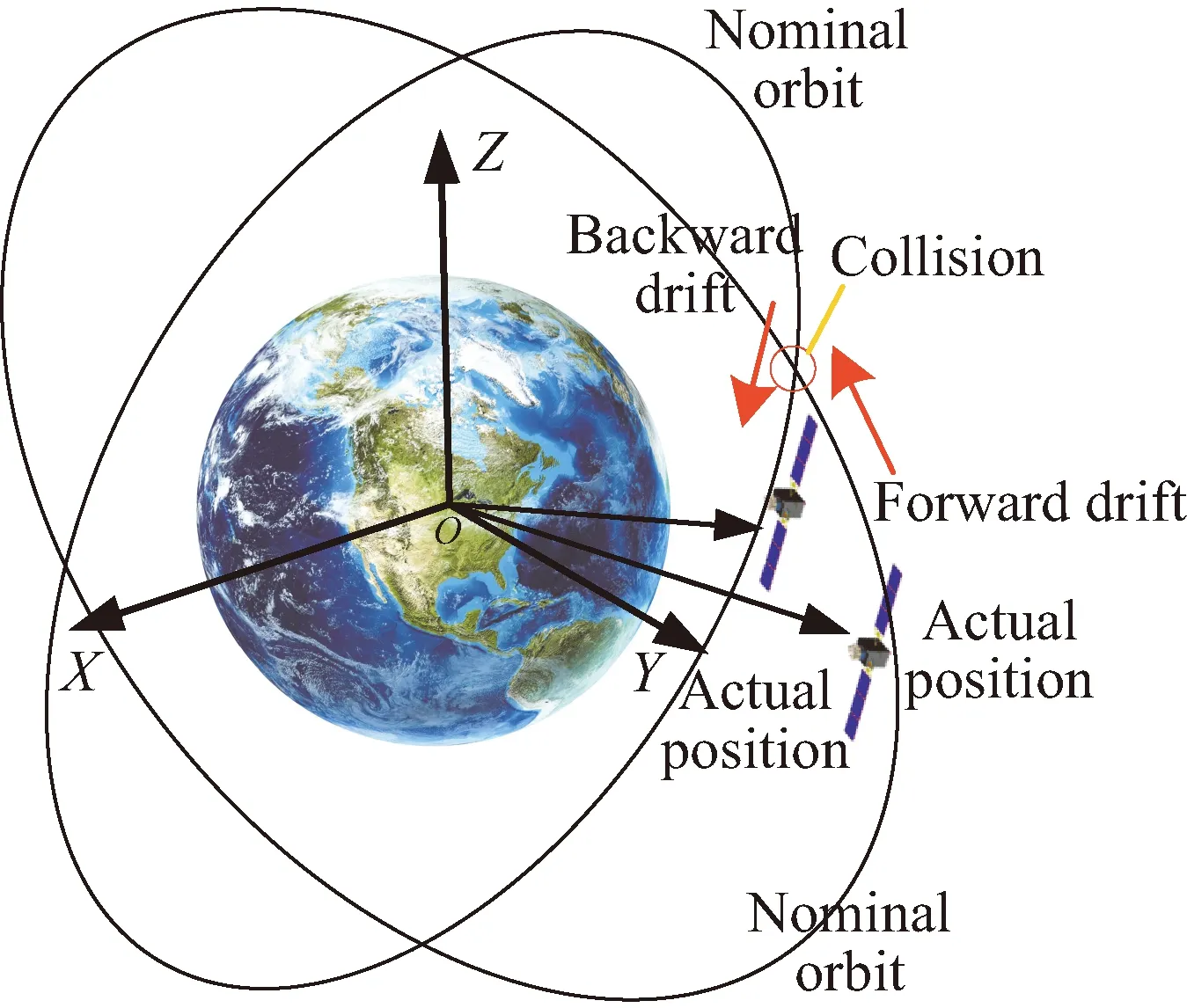
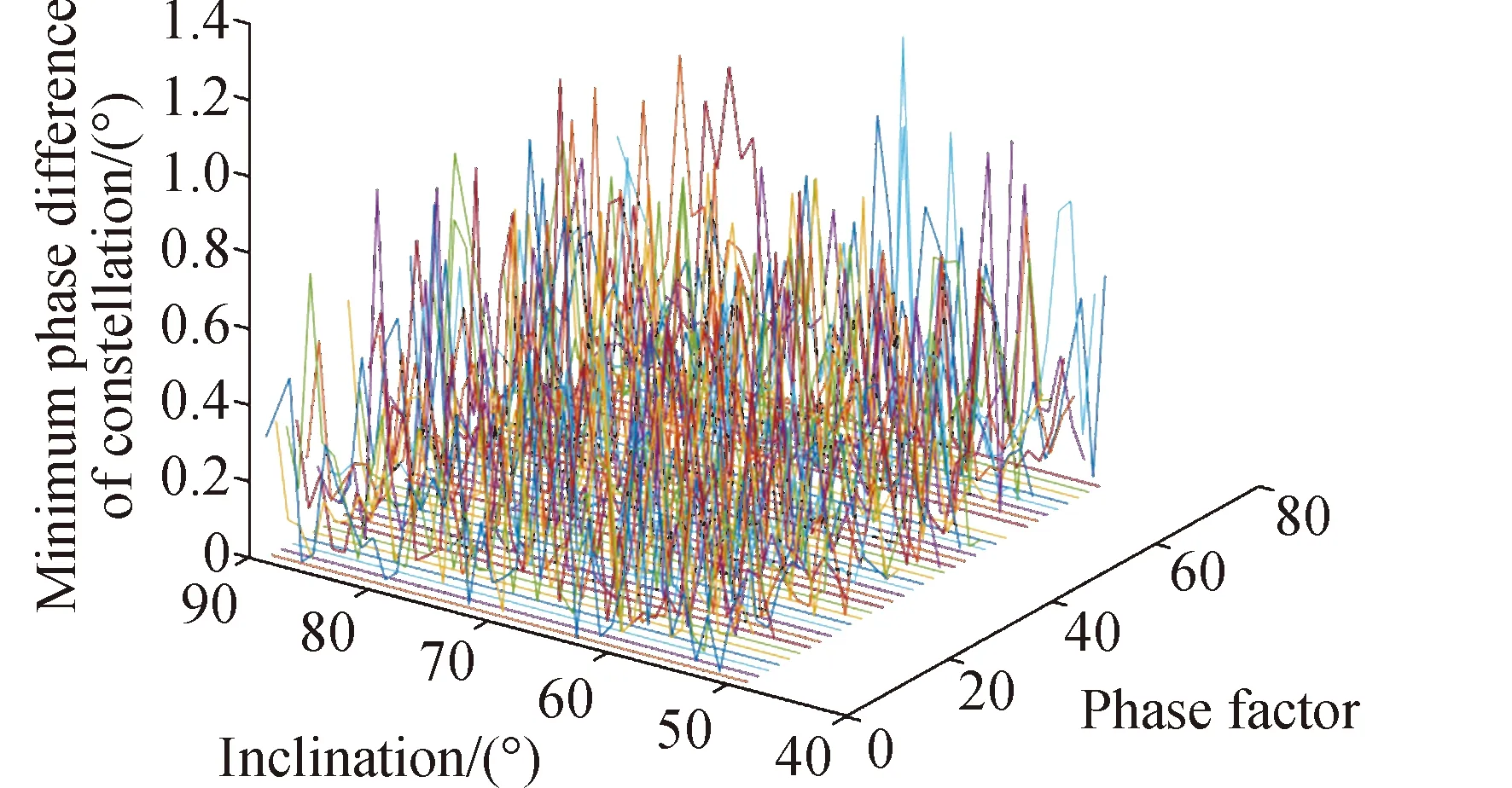
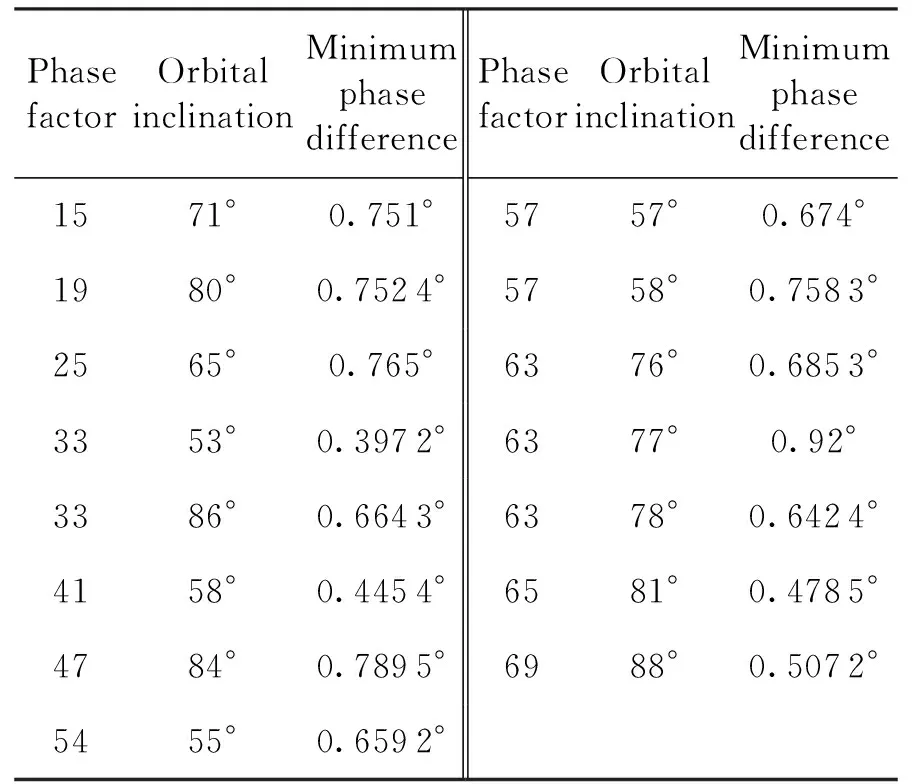
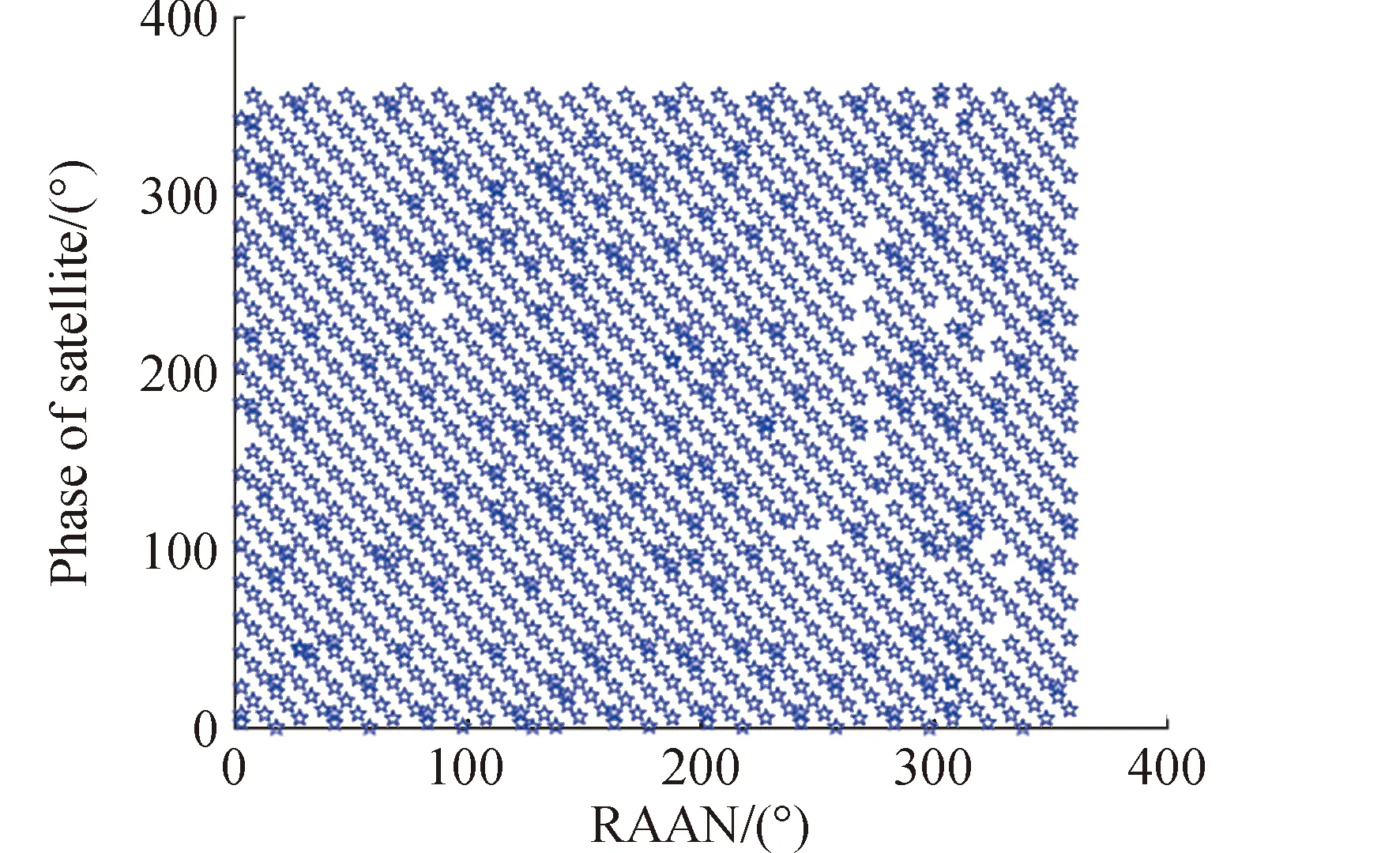
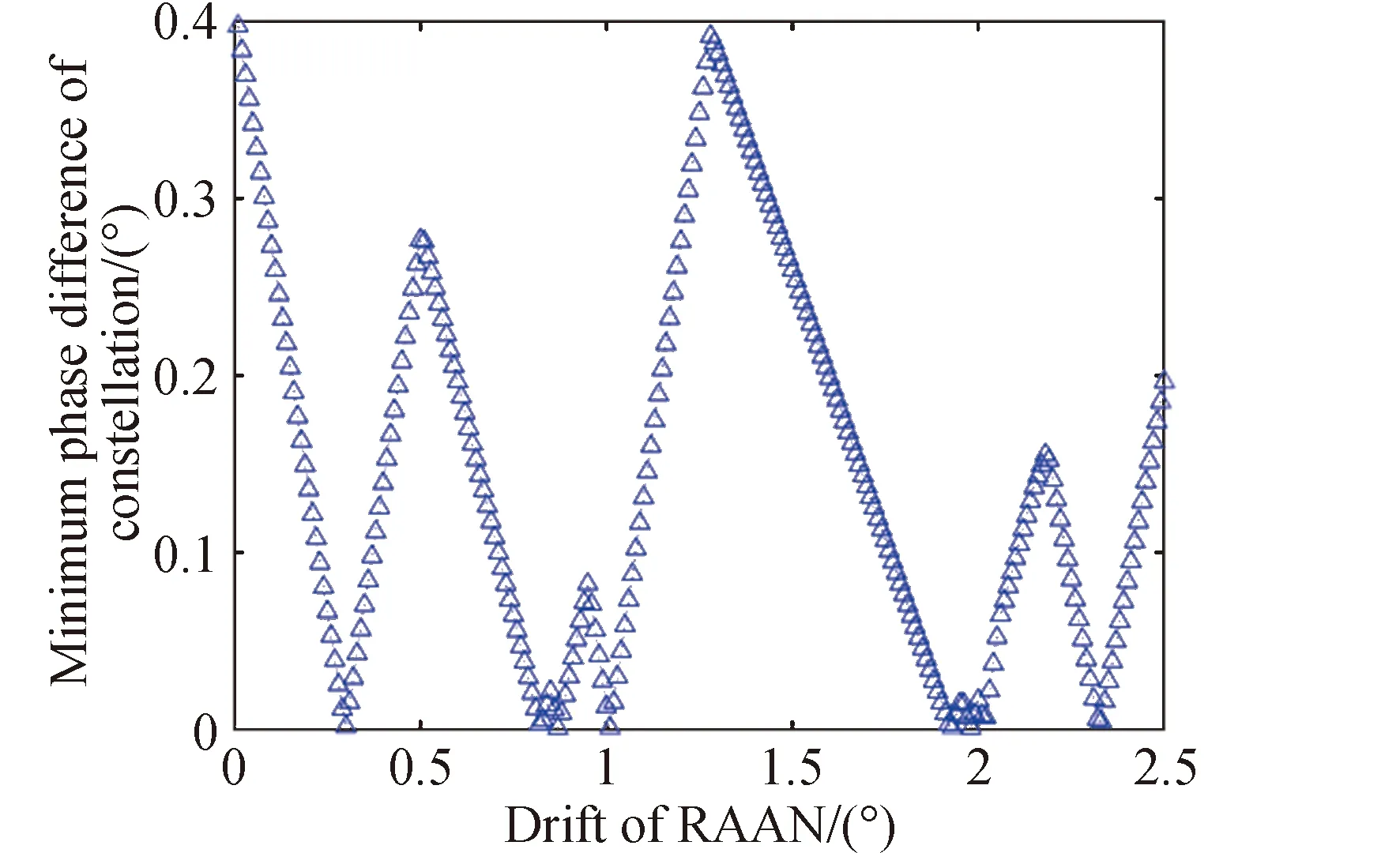
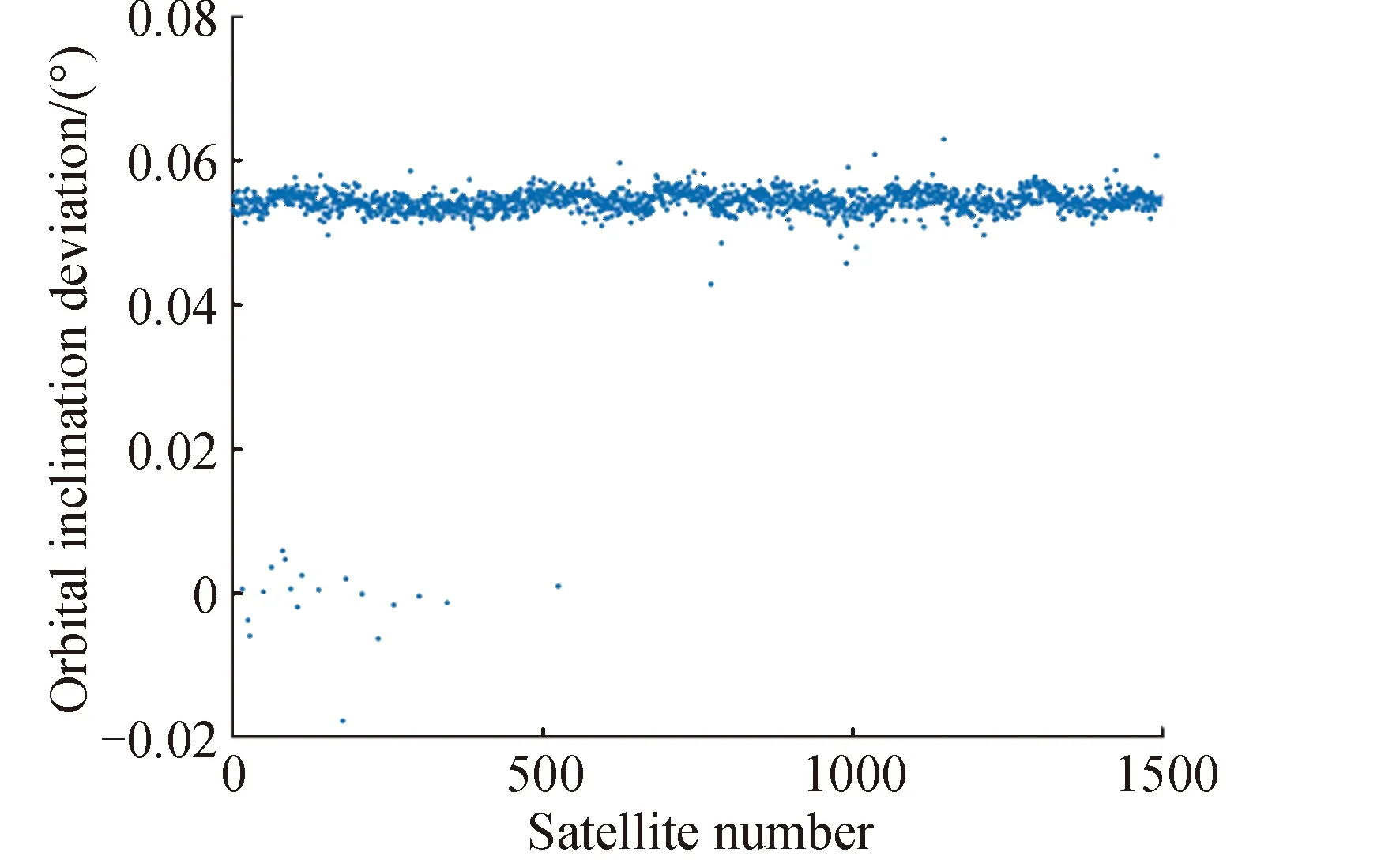
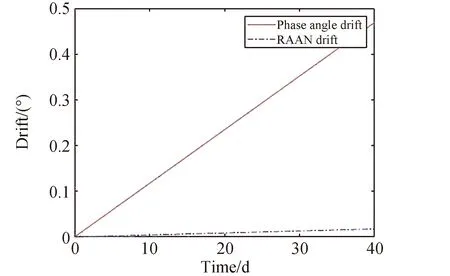
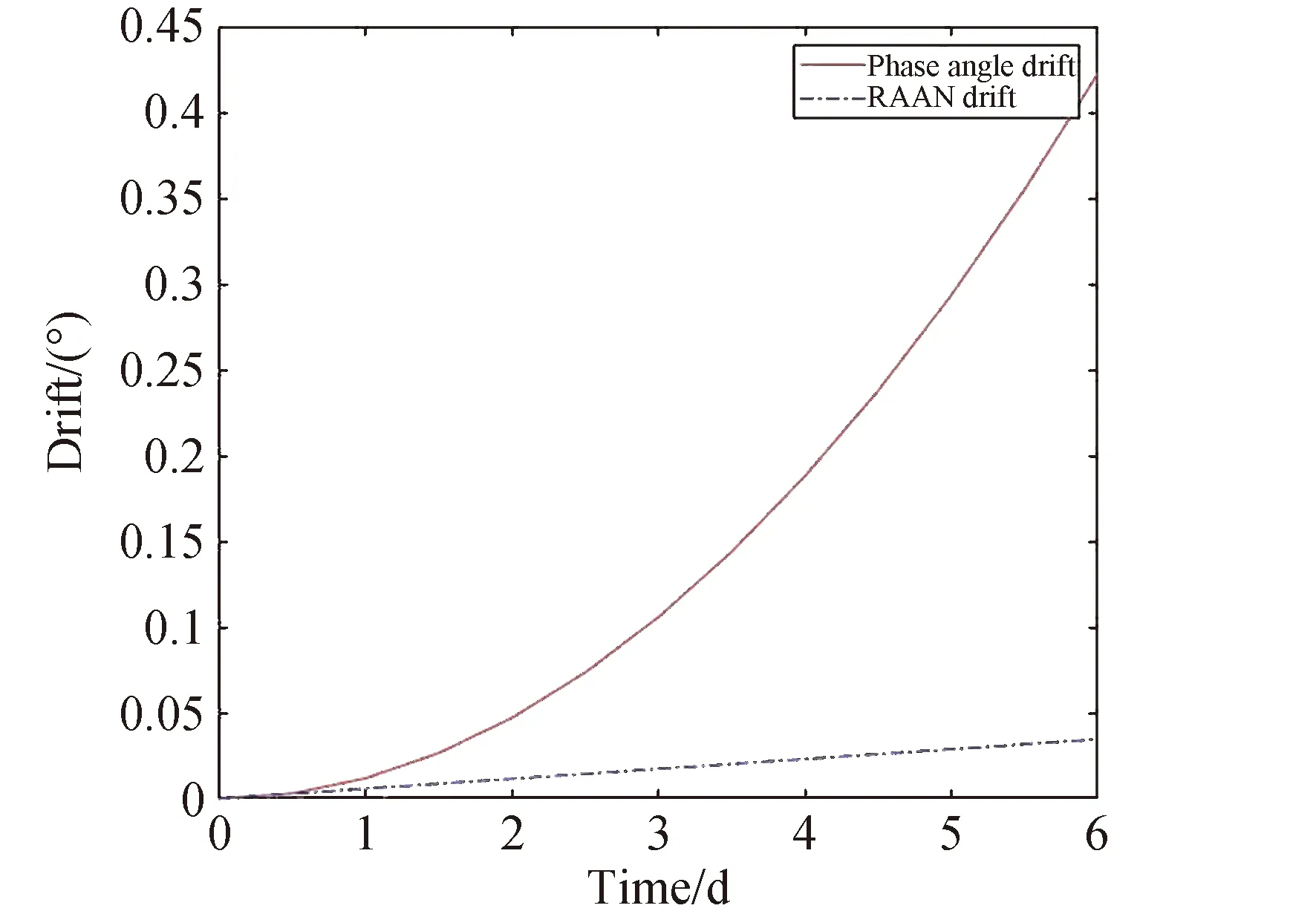
假设星座标称构型参数为N/P/F,轨道倾角为i。根据星座结构参数得到星座在标称构型条件下相邻轨道平面间的升交点赤经差为360/P,因此,对标称轨道下任意两轨道平面j,k(j (11) 令星座卫星升交点赤经漂移量为ΔΩ,假设星座相邻轨道平面卫星的漂移约束条件为轨道平面不会重合,因此,可以推导出星座卫星升交点赤经漂移量约束为0≤ΔΩ<180/P,根据星座卫星升交点赤经漂移约束,得到任意两轨道平面j,k的实际升交点赤经差范围为: (12) 令卫星数量N为1200,轨道面个数为60,相位因子F=1,轨道倾角为60°,仿真在不同升交点赤经漂移量下,相邻轨道平面卫星最小相位差,得到如图6所示的关系图。 图6 升交点赤经漂移量与相邻轨道平面卫星最小相位差关系Fig.6 The drift of RAAN and the minimum phase difference of satellites in adjacent orbital planes 从图6可以看出,升交点赤经漂移量与相邻轨道平面卫星间最小相位差呈线性关系,在与其他卫星发生交会前,升交点漂移量越大,轨道平面卫星相位差越小。将升交点赤经漂移量与相邻轨道的最小相位差拓展到所有轨道平面时,可以得到星座最小相位差随升交点赤经漂移量的变化曲线如图7所示。 从图中可以得到,星座卫星保持在左边直线下方范围内漂移时,卫星不会与其他卫星发生碰撞,能够保证星座卫星运行安全,而当最小相位差达到0时,表示两卫星之间发生了碰撞,因此需要将最小相位差维持在第一次达到0之前的范围。而在这个区间内,升交点赤经漂移量与星座卫星间最小相位角之间满足线性约束关系,即: φc=aΔΩ+b (13) 式中:φc为星座最小相位差;a,b为线性约束的系数;ΔΩ为升交点赤经漂移量。 低轨大规模星座在实际运行过程中,由于误差的存在,星座卫星间的轨道位置存在偏差,在摄动力的作用下,卫星间会产生相对漂移,在星座构型约束下,卫星相对位置漂移达到一定程度就可能导致与其他轨道平面卫星间发生碰撞,因此,需要将低轨大规模星座卫星的漂移约束在一定范围内。图8为卫星位置偏差引起的碰撞示意。 图8 卫星位置偏差引起的碰撞示意Fig.8 Schematic diagram of collision caused by satellite position deviation 低轨卫星主要受到地球非球形摄动、大气阻力摄动的作用,其中地球非球形摄动会引起相位漂移和升交点赤经漂移,大气阻力摄动不会引起升交点赤经漂移,但可以通过影响轨道半长轴间接引起相位漂移。摄动力引起的平均轨道根数长期变化率为: (14) 对于低轨大规模星座,其偏心率可以近似为0,因此,升交点赤经漂移速率和相位漂移速率主要和轨道半长轴以及轨道倾角相关。由于大气阻力比较复杂,大气引起的轨道衰减造成的半长轴变化也比较复杂,根据文献可知,两卫星相位漂移量Δu主要和两卫星之间的平半长轴偏差相关,其公式为: (15) 式中:μ为地球引力常数;t为时间;Δa为两卫星相对半长轴偏差。升交点赤经漂移量ΔΩ为: (16) 为了保证低轨大规模星座轨道安全,需要对卫星进行机动控制,以维持星座构型的稳定。常用的星座构型保持策略有绝对构型保持策略和相对构型保持策略。绝对构型保持策略要求卫星的实际位置与设计轨道保持在一定范围内,保证星座构型与设计构型一致;相对构型保持策略要求卫星的实际位置相对于基准卫星的位置保持在一定范围内,保证星座的相对构型保持一致。 由文献[21]可知,绝对控制策略下的最大漂移量可根据“死区”的概念求解。由于星座各卫星相对标称轨道的漂移是相互独立的,保证每颗卫星的相位角漂移量为最小相位差的1/2以内,就可以避免在轨道平面交点处的相遇,因此,可以得到星座最大相位角漂移量θu为: (17) 相对控制策略下的最大漂移量根据卫星的相对运动求解,卫星的最小相位差为卫星相对运动能够达到的最大值,因此,星座的最小相位差为卫星相对相位最大漂移量θu,rel的约束,即: θu,rel=φc (18) 根据升交点赤经漂移量和最小相位差的约束关系以及升交点赤经和相位随时间漂移关系式,可以得到,当等式Δu(t)=aΔΩ(t)+b成立时,升交点赤经和相位角达到最大漂移量,同时也可以得到星座构型维持控制一次的间隔时间。 一般情况下,星座卫星数量和轨道平面数量的设计主要与星座想要达到的性能相关,因此,星座构型安全主要与构型参数中的轨道倾角和相位因子相关。本章以Starlink一期星座为研究对象,研究星座卫星数量和轨道平面数量不变的情况下,基于最小相位差的星座构型参数协同设计方法以及Starlink星座构型参数条件下的最大容许漂移量和不同控制策略下的维持控制时间周期。 通过查阅文献资料可以得到Starlink一期星座卫星数量为1584颗,轨道面数量为72,轨道倾角为53°。下面仅根据星座卫星数量和轨道面数量讨论相位因子和轨道倾角对星座最小相位差的影响,考虑到美国本土最大纬度为49°,因此,轨道倾角仿真范围为[49°,89°],得到不同相位因子和轨道倾角下与星座卫星最小相位差的关系如图9所示。 图9 不同相位因子和轨道倾角下星座卫星最小相位差Fig.9 Minimum phase difference of constellation under different phase factors and orbital inclination angles 图9中,自变量为相位因子和轨道倾角,因变量为星座卫星间最小相位差,通过计算固定相位因子下不同轨道倾角的最小相位差,可以得到每个相位因子下不同轨道倾角的星座最小相位差分布曲线。 由图9的数据可知,不同相位因子和轨道倾角下星座最小相位差相差较大,为保证星座的鲁棒性,防止因为误差或摄动力对轨道倾角的影响使星座最小相位差发生较大波动,对数据进行了以下处理:将同一相位因子下,以连续三个轨道倾角采样点的值都大于0.37°作为约束条件(根据数据情况取值为0.37°)。对不满足的数据进行剔除,然后只保留三个数中处于中间的数,经过处理后,得到的满足最小相位差条件的相位因子和轨道倾角数据如表1所示。 表1 满足最小相位差条件的相位因子和轨道倾角Table 1 Phase factor and inclination satisfying the minimum phase difference condition 其中0.37°是根据图9中的计算数据来估计取值的,但是只是一个估计值,并不是唯一确定值。取值0.37°的原因如下:一方面,根据已有数据结果情况进行判断,由于小于0.37°的数据量较大,若取值小于0.37°,会有很多组数据满足条件,因此为了剔除无效的数据,取值需大于或等于0.37°;另一方面,根据Starlink一期计算的结果为0.3972°,为保留Starlink的这组数据,取值需小于0.3972°。约束条件的取值是一个范围,在0.37°到0.3972°之间,在本文中作者取了较小值0.37°。 由于Starlink星座相位因子的公开资料较少,本文将通过对Starlink星座已部署构型进行反演求其相位因子。通过SpaceTrack网站下载了Starlink星座卫星2022年3月17日的TLE数据,将数据导入STK,并演化数据到同一时间输出,得到星座构型情况如图10所示。 图10 Starlink星座构型部署Fig.10 Starlink constellation configuration deployment diagram 从表1可得,若仅从星座构型安全的角度出发,选择相位因子63,轨道倾角为77°的参数更能保证星座的安全,但星座设计还需要综合考虑星座服务性能、链路性能、稳定性能、可拓展性等各方面因素,Starlink星座经过综合考虑过后选择相位因子33,轨道倾角53°的构型参数,也是星座构型安全较优的解之一,证明了协同设计方法的合理性。 接下来求解Starlink星座构型参数条件下不同控制策略下的最大容许漂移量和维持控制时间周期。根据Starlink星座结构参数仿真分析,可以得到Starlink星座升交点赤经漂移量与最小相位角的约束关系如图11所示。 图11 Starlink星座升交点赤经漂移量与星座最小相位差关系Fig.11 Relationship between drift of RAAN and minimum phase difference of constellation(Starlink) 根据图11可知,升交点赤经漂移量会引起最小相位差的波动变化,但在实际情况下,当最小相位差为0时,代表卫星之间已经发生碰撞,为了保证星座构型安全,需要控制升交点赤经漂移量维持在最小相位差第一次达到0之前。因此,图11中左边的第一条直线为最小相位差与相位漂移量的有效约束曲线,根据曲线上的两点,可以得到Starlink星座升交点赤经漂移量与相位漂移量的关系为: Δu=-1.357ΔΩ+0.409 (19) 然后,根据Starlink星座升交点赤经漂移量与相位漂移量之间的约束关系,求解绝对控制策略和相对控制策略下Starlink星座最大漂移量和星座实施维持控制的时间频率。 将工作轨道上Starlink星座卫星TLE数据中的轨道倾角减去设计轨道倾角,可以得到星座卫星相对标称轨道的倾角差。倾角差如图12所示,从图中可以看出,卫星实际轨道倾角与设计轨道倾角平均偏差约为0.054°,两卫星轨道倾角相对平均偏差约为0.004°。假设两卫星初始半长轴相对偏差为10m,相对控制策略下两卫星在轨道衰减过程中的相对半长轴偏差近似保持不变,可得到相对控制策略下升交点赤经和相位角随时间的漂移情况。图13给出了漂移量随时间变化的曲线图。 图12 Starlink卫星轨道倾角偏差Fig.12 Starlink satellite orbit inclination deviation 图13 相对控制策略下升交点和相位漂移量随时间变化Fig.13 Ascending intersection and phase drift change with time(relative control strategy) 卫星实际轨道倾角与设计轨道倾角平均偏差约为0.054°,假设卫星初始半长轴相对标称轨道为10m,由于Starlink星座卫星所在轨道高度的每天轨道衰减量约为10m,因此近似考虑卫星每天轨道高度衰减量为10m,可得到绝对控制策略下升交点赤经和相位角随时间的变化情况。图14给出了漂移量随时间变化的曲线图。 图14 绝对控制策略下升交点和相位漂移量随时间变化Fig.14 Ascending intersection and phase drift change with time(absolute control strategy) 根据图13和图14可知,相对控制策略下,升交点赤经漂移曲线呈线性,相位漂移曲线也为线性。Starlink星座卫星升交点赤经和相位最大漂移量分别为0.01°和0.38°,实施一次维持控制的时间间隔约为33d。绝对控制策略下,升交点赤经漂移曲线呈线性,相位漂移曲线呈抛物线,Starlink星座卫星升交点赤经和相位最大漂移量分别为0.03°和0.15°,实施一次维持控制的时间间隔约为4d,若对相位进行偏置控制,控制时间可以延长到约8d维持控制一次。对比两种控制策略,可以得到,在相同星座构型参数约束条件下,相对控制策略能够有效延长星座构型控制时间。 绝对控制策略下,本章计算得到Starlink星座卫星升交点赤经和相位最大漂移量分别为0.03°和0.15°。文献[15]给出了Starlink卫星相邻卫星相位差基本维持在±0.2°,可以得到计算出的结果能够保证星座内部安全,结果具有合理性。 本文通过对低轨大规模星座构型参数进行分析,得到轨道倾角和相位因子能够协同调节星座最小相位差的大小,提出了基于星座构型安全的构型参数协同设计方法。仿真试验表明,通过协同设计能够得到不同轨道倾角和相位因子下星座最小相位差较优的结果,给出满足星座构型安全的构型参数,为星座构型参数设计提供参考。 当确定星座构型参数以后,根据星座最小相位差与升交点赤经漂移量之间的约束以及升交点赤经和相位差随时间的漂移关系,可以得到星座构型升交点赤经和相位最大漂移量,以及不同维持控制策略下的维持控制时间频次。 通过对Starlink第一期星座进行仿真得到,绝对控制策略下升交点赤经和相位最大漂移量分别为0.03°和0.15°,构型维持频次约为4d一次,若对相位进行偏置控制,控制时间为约8d维持控制一次。相对控制策略下升交点赤经和相位最大漂移量分别为0.01°和0.38°,构型维持频次约为33d一次,与绝对控制策略相比,相对控制策略能够有效延长星座构型维持控制时间。 根据星座构型最大漂移量及维持控制时间,可以得到低轨大规模星座构型安全评价指标,为低轨大规模星座卫星间碰撞安全评估提供参考。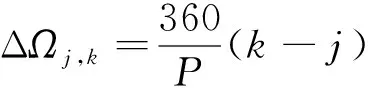
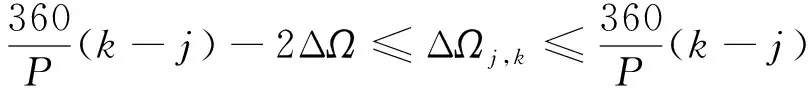
4 星座最大漂移量分析
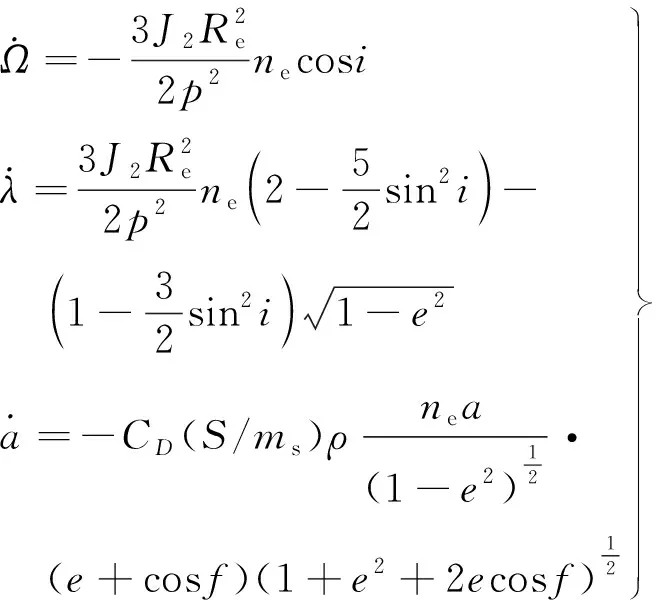
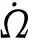
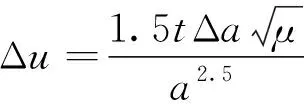
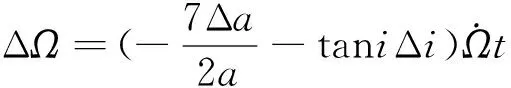
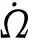
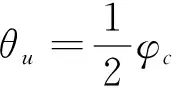
5 仿真分析
5.1 基于最小相位差的星座构型参数协同设计
5.2 最大漂移量仿真分析
6 结论

