基于GPU的并行相位解卷绕算法

毛飞龙,焦义文,马宏,*,张宇翔,聂欣林,高泽夫

1.航天工程大学 电子与光学工程系,北京 101416 2.国防科技大学 电子科学学院,长沙 710072 3.吉林大学白求恩第一医院,长春 130000

1 引言

随着航天技术与深空探测技术的迅猛发展,各国对空间的探测向着更深更远的范围拓展。探测目标向火星以及更遥远的太阳系大天体延伸,探测距离将从目前月球探测的4×105km拓展到火星探测的4×108km和木星探测的109km。距离越远,信号到达地面的增益越低,这将对地面接收设备带来巨大挑战。通过天线组阵信号合成方法获得更高的深空通信增益是值得大力发展的方法。天线组阵中的一项关键技术是信号间相位差估计,两天线接收到同一信源的信号,互相关运算得到天线间的互相关谱,之后经过反正切相位鉴别器求得天线间的相位差。由于反正切运算的存在,获得的相位值被限制在[-π,π]之间。这些处于[-π,π]之间的相位就被称作卷绕相位,为了得到真实的相位值信息,就必须将卷绕相位恢复为真实值,该过程就是相位解卷绕。

在行星探测任务中,探测器的跟踪及精密测定轨在任务中占据重要地位,是完成工程任务和科学探测的基础。中国嫦娥四号任务相时延处理软件中,探测器卷绕相关相位的范围是[-π,π],也需要进行解卷绕处理。相位解卷绕对于探测器的定位和定轨,特别在探测器变轨、捕获及下降着陆等关键弧段至关重要。因此,如何准确且快速地进行相位解卷绕对深空天线组阵信号合成、行星探测任务的变轨、捕获等具有重要的工程意义。此外,相位解卷绕还是阵列信号相位差估计[1]、无线电干涉测量[2-5]、光学干涉仪[6-10]、核磁共振成像[11-14]等技术中的一个关键且基础的算法。

在干扰较小时,只要从相位的第一个值开始逐点向后判断并通过加减2π还原真值就可完成解卷绕。但信号处理、光学成像等系统对实时性的要求较高,使用上述的串行算法对大量数据进行解卷绕将导致实时性急剧恶化。而目前对解卷绕的研究主要集中在提升其抗干扰性能[15-18],关于相位解卷绕并行实现的研究较少。因此,迫切地需要寻求一种准确性好、实时性强的解卷绕方法。

近年来,随着高性能计算的发展,图形处理器(graphic processing unit,GPU)从专用于图像领域的处理器逐渐向着通用并行计算平台转变。GPU已发展成为一种高度并行化、多线程、多核的通用计算设备,具有杰出的计算能力和极高的存储器带宽,并被越来越多地应用于图形处理之外的计算领域。GPU的运算核心数远多于CPU,更适合于数据密集型计算的并行加速处理。NVIDIA于2007年推出了计算统一设备架构(compute unified device architecture,CUDA),简化了GPU系统的开发流程,使得GPU通用计算技术在信号处理领域得到更为广泛的应用。目前,基于GPU的信号处理系统具有强大的并行处理能力,能够在短时间内通过并行处理完成大量数据的运算,在GPU资源得到充分利用时,可以实现对信号的实时处理要求。因此,基于GPU的信号处理技术成为众多领域的热点,如射电天文[19-20]、雷达[21-31]、无线通信[32-33]、人工智能[34-35]等。

本文以串行解卷绕算法为基础,通过对算法的并行映射寻求对实时性能的提升。本文在GPU平台下设计了一种通用的并行相位解卷绕算法,并验证了算法的正确性与实时性。

2 相位解卷绕算法研究

2.1 相位卷绕现象分析

相位卷绕现象一般出现在反正切相位鉴别之后,相位的主值被限制在了[-π,π]之间。这些被限制在[-π,π]之间的相位,与真实的相位相差2k·π(k为整数)[4]。假设真实的相位为θ,卷绕的相位为φ,则有:

θ=φ+2k·π

本文将常见的相位卷绕现象分为两类,分别为直线型相位卷绕和曲线型相位卷绕。直线型相位卷绕主要出现在干涉测量中,表现为直线的截断。曲线型相位卷绕主要是余弦波形的相位卷绕,如旋转相位干涉仪的卷绕现象,就是典型的曲线型相位卷绕[36],表现为对余弦波形的截断。图1为相位卷绕示意图,图1(a)为直线型相位卷绕原始信号波形,图1(b)为其卷绕后的相位图像。图1(c)为曲线型相位卷绕原始信号波形,图1(d)为其卷绕后的相位图像。图中两条虚线表示[-π,π]范围,可见卷绕后的相位值被限制在了该范围内。

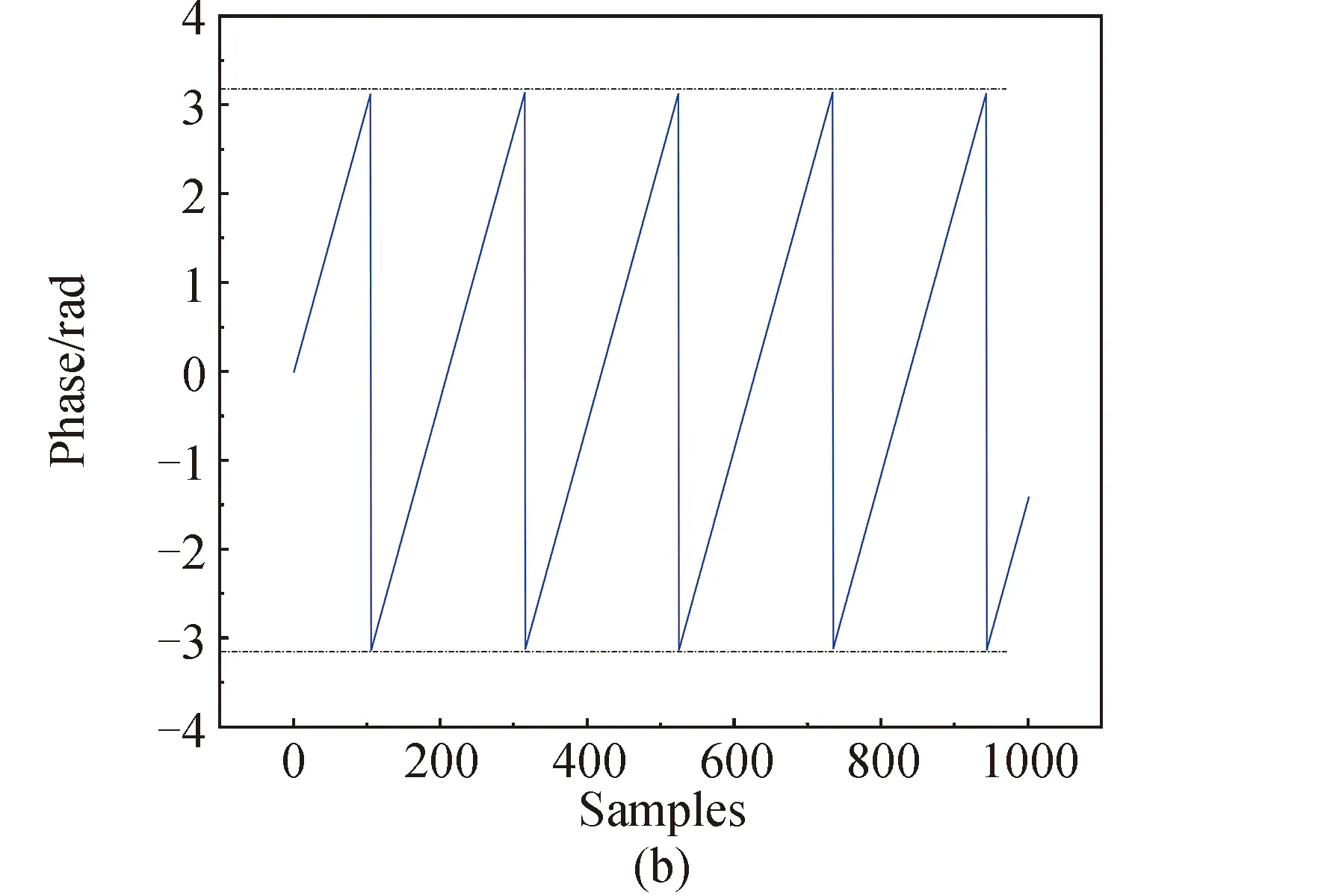
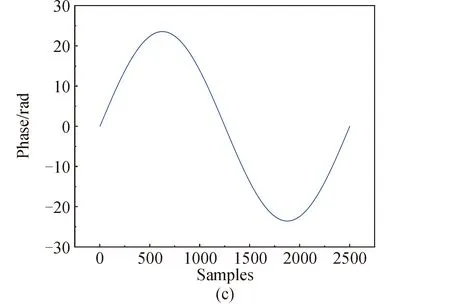
图1 相位卷绕现象示意Fig.1 Schematic of phase wrapping

2.2 相位解卷绕方法

目前,相位解卷绕的方法有很多,包括连续逐点解卷绕方法、拉普拉斯相位解卷绕方法等。其中最常用的方法就是通过逐点判断并还原真实相位值的解卷绕方法。在卷绕相位中,由于发生卷绕点的相位会出现正负2π的跳变现象,而未发生卷绕的区域相位是近似连续的。因此,可以通过相邻相位值之间的差来判断是否出现相位跳变现象,也即卷绕现象。之后将卷绕的相位值通过加减2π来得到连续的、非卷绕的相位曲线。在一些文献中,这种方法也被称作区域生长法。

具体步骤为:如果相位卷绕图中相邻相位发生了大于+π的跳变量,则从跳变点开始后面所有相位值全都减去2π,如果相位跳变小于-π,则从跳变点开始后面所有相位全都加上2π,相邻相位之间的差值处于-π和+π之间则不做处理,逐点处理完所有相位即完成相位解卷绕。

旋转单基线可以利用数字积分器进行相位的累加处理以达到解卷绕的作用。一种典型的数字积分器计算公式如(1)所示[37]。

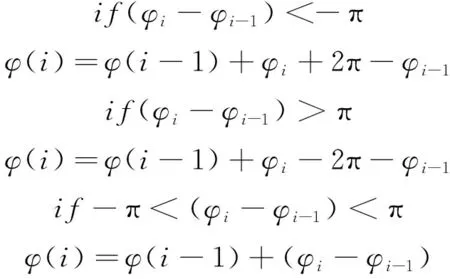
(1)

式中:φi是当前时刻的相位差,φi-1是上一时刻的相位差,φ(i)是积分器当前累加的相位差,φ(i-1)是积分器上一次的相位差。该算法也是通过逐点判断两点间的相位差并还原来实现解卷绕。

在连续逐点解卷绕方法中,由于是对相位信息的逐点解卷绕,得到的解卷绕的结果非常准确,但是由于该方法属于串行过程,导致解卷绕的速度非常缓慢,限制了其在实时性要求较高的场景使用。拉普拉斯方法是由严格的数学公式推导而来,是对纯数学公式的应用,因此其解卷绕的速度明显快于连续逐点解卷绕方法,不足之处就是拉普拉斯方法解卷绕准确性不如连续逐点解卷绕方法,高频区域的处理结果过于平滑。

本文旨在寻求一种准确性好、实时性强的解卷绕方法。因此,本文尝试在连续逐点串行解卷绕算法的基础上,设计一种基于GPU的并行相位解卷绕方法。

3 并行相位解卷绕算法设计

3.1 算法并行性分析

在串行连续逐点解卷绕方法中,要确认某一相位值是否卷绕,就要判断该值与上一相位值的差是否在[-π,π]之间。主要有三种情况,若差值大于π,则该点有卷绕现象,此时卷绕相位的大小为真实相位值加2π所得的数值;若差值小于-π,则该点也有卷绕现象,此时卷绕相位的大小为真实相位值减2π所得的数值;若差值在[-π,π]范围内,则该点不存在卷绕现象,不需要进行解卷绕。串行连续逐点解卷绕方法对某一值解卷绕时需满足其之前的所有值均为真实相位值(不存在卷绕现象),因此,该方法只能从头到尾逐次进行解卷绕,其耗时的主要原因也就在于此。

针对传统方法串行的处理方法,若能将串行的处理过程转化为对所有点的并行解卷绕,即可很好地解决实时性差的问题。

对解卷绕过程分析可知,对存在卷绕现象的某一值解卷绕时只需确定其与真实相位的偏差。利用该偏差值对卷绕相位进行补偿,即可完成该点的解卷绕。而在该卷绕相位之后至下一卷绕相位之间范围内(即不存在卷绕现象的范围)各点的补偿值与该卷绕相位的补偿值相同。如图2所示,将所有相位值按卷绕相位出现的位置分为6组(图中六种不同颜色表示)。其中第1组不存在卷绕现象,不需要解卷绕,第2、3、4、5、6组的第1个相位发生了卷绕,需要进行解卷绕处理。每组的补偿值相同,只需计算出第一个卷绕相位的补偿值即可。

图2 直线型相位解卷绕示意Fig.2 Schematic of linear phase unwrapping

因此,要实现对各点的并行解卷绕,找出发生卷绕现象的位置并计算出各个卷绕相位的补偿值是关键所在。

下面对直线型卷绕的补偿值进行分析,从第2组开始,每组的第1个相位为卷绕相位。第1组不需要解卷绕,补偿值为0;第2组相位值向下跳变了2π,因此该组的补偿值为2π×1;同理,第3组的补偿值为2π×2;第4组的补偿值为2π×3。

图3为曲线型相位解卷绕示意图,下面对曲线型卷绕的补偿值进行分析,从第2组开始,每组的第1个相位为卷绕相位。第1组不需要解卷绕,补偿值为0;第2组相位值向下跳变了2π,因此该组的补偿值为2π×1;同理,第3组的补偿值为2π×2;第4组相位值向上跳变了2π,其补偿值为上一组补偿值的基础上减2π,因此,第4组的补偿值为2π×1;同理,第5组的补偿值为0。

综合两种类型的卷绕现象可以得出,按卷绕点相位出现的位置进行分组后,每组的补偿值由之前所有卷绕点(包括当前组的)的数量和卷绕类型决定。定义卷绕相位的卷绕类型:0为未发生卷绕,-1为向下跳变,1为向上跳变。设某一相位序列A为:

A={x1,x2,x3,…,xL}

定义序列A中各相位的卷绕类型构成的序列为B:

B={a11,a12,a13,…,a21,a22,a23,…,a31…}

其中,aij代表第i组的第j个值。由于每组有且只有第1个相位为卷绕相位且第1组未发生卷绕现象。则B可化简为:

B={a11,0,0,…,0,a21,0,0,…,0,a31…}

其中,a11=0,则第n组的解卷绕补偿值valuen为:

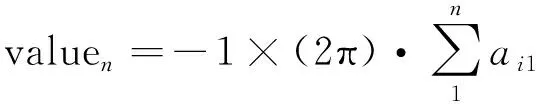
(2)

当卷绕相位为直线型时,所有分组的补偿值相同,解卷绕补偿值valuen可进一步化简,其中k为直线斜率:

当卷绕相位为曲线型或任意卷绕类型时,解卷绕补偿值通过式(2)计算得出。显然,所有点的补偿值序列offset为:

offset={value1,…,value2,…,valuen,…}

(3)

根据offset序列对所有点并行进行补偿(将现有相位与补偿值相加),即可实现对所有相位的并行解卷绕。

Aunwrap=A+offset

(4)

3.2 算法实现流程

本文设计的基于GPU的相位解卷绕算法,相比于基于CPU的算法,主要改进如下:利用GPU众核优势,将解卷绕算法拆分为3个独立的模块,分别使每个模块进行多线程并发。传统算法按数据的顺序依次进行获取卷绕信息、建立补偿值、进行补偿三个模块。本文中的并行算法不再按照数据点的顺序进行运算,而是根据3.1节中公式推导结果对所有数据点同时获取卷绕信息,在得到所有点的卷绕信息之后,根据卷绕点的数量和位置将数据进行分组,利用多个线程同时对不同的分组赋予不同的补偿值。最后并发多个线程对所有点进行相位补偿。

图4为并行相位解卷绕实现流程,具体可分为以下步骤:

图4 并行相位解卷绕实现流程Fig.4 Implementation of parallel phase unwrapping

步骤1:设原始相位序列的长度为L。调用L个线程,判断所有相邻相位值之间的差是否在[-π,π]范围内从而获取所有卷绕点的信息。包括卷绕点的位置、卷绕类型和卷绕点数量。

步骤2:按照卷绕点出现的位置对相位序列进行分组,n个卷绕相位可分为n+1组。

步骤3:调用n+1个线程,根据公式(3)计算出各组的解卷绕相位补偿值value,并根据公式(3)建立所有点的补偿值序列offset。

然而笔者认为，两个罪名不仅调整范围相差甚异，而且各自有行为的评价侧重点。比较二者的客体不同点即可看出:

步骤4:调用L个线程,根据公式(4)对所有相位值进行补偿。

以上步骤将并行解卷绕过程拆分为三个模块:获取卷绕模块、建立补偿模块、并行补偿模块,分别命名为get_wrap、get_offset、parallel_unwrap。

4 算法GPU实现

本节主要讨论如何基于GPU的编程架构对解卷绕算法进行并行设计优化,以进一步提高运算效率,满足实际工程应用中的实时信号处理需求。

4.1 并行优化设计

CUDA是以大量线程来实现高吞吐量数据的实时并行处理,线程间越独立,加速的效果越明显。根据上文对算法并行性的分析,每个模块内每个线程的运算都是独立的。因此,本文设计的并行解卷绕算法适合用GPU进行并行加速,可以极大地提高运算效率,为后续信号处理的实时处理打下基础。

图5为GPU并行优化示意图,首先通过CPU分配好主机内存和设备内存,初始化各个变量。并利用cudaMemcpy将原始卷绕相位序列写入GPU片上内存。在实际处理过程中,由于GPU的线程数目有限,根据原始相位序列的长度选取GPU的数量。在每个GPU中以单指令多数据流(single instruction multiple data,SIMD)并行架构进行各模块的运算。所有模块计算完成后,将解卷绕后的序列传回CPU内存或继续在GPU中进行后续的处理。

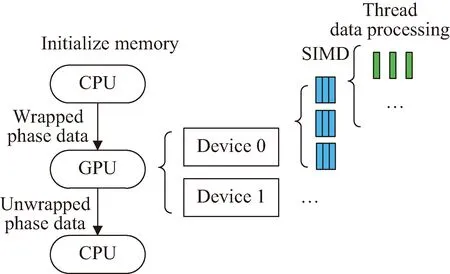
图5 GPU并行优化示意Fig.5 Schematic of GPU parallel optimization

4.2 获取卷绕模块GPU实现

并行解卷绕算法的第一个模块就是获取卷绕相位信息,卷绕信息包括卷绕点的位置、卷绕类型和卷绕点数量。定义结构体Wrap,包含id和type数据项,分别对应卷绕的位置和类型。如算法1。

算法1:获取卷绕相位

Input:wrap_data、size

struct Wrap { int id;int type;};

__global__ void get_wrap(double *wrap_data,float *difference,Wrap *wrap,int size,int num)

{int tid = blockIdx.x * blockDim.x + threadIdx.x;

if(tid >= size - 1) return;

difference[tid + 1] = wrap_data[tid + 1] - wrap_data[tid];

if(difference[tid + 1] >CU_PI)

temp = atomicAdd(num,1);

wrap[temp].id = tid + 2; wrap[temp].type = 1;

if(difference[tid + 1] <-CU_PI)

temp = atomicAdd(num,1);

wrap[temp].id = tid + 2; wrap[temp].type = -1;

sort(wrap,wrap + num);

wrap_data为初始相位序列,size为该序列的长度,difference为相邻两个相位之间的差,wrap为输出的卷绕信息结构体序列,num为卷绕点的数量。调用size个线程,每个线程分别获取各点卷绕信息,达到并行运算的目的。每个线程内的具体操作为:首先计算出该点与前1相位的差值difference,通过判断该值是否在[-π,π]范围内,来判断该点是否为卷绕点。若是卷绕点,则将该点的位置和卷绕类型写入卷绕信息序列wrap。

由于线程并发时,存在多个线程同时访问wrap内存的问题,即访问冲突导致写入数据出错的问题。采用原子操作方法进行解决,原子操作是指不会被线程调度机制打断的操作;这种操作一旦开始,就一直运行到结束,中间不会有任何context switch(切换到另一个线程)。在多进程(线程)访问共享资源时,能够确保所有其他的进程(线程)都不在同一时间内访问相同的资源[38-42]。本文使用atomicAdd原子相加操作,确保各个线程不会同时访问wrap,进而得到所有卷绕点的信息。

同时,由于各个线程运算结束的时间也各不相同,这就导致所有线程运算完成后,得到一个无序的卷绕信息序列。需要进一步对wrap序列按照其id数据项进行排列。

4.3 建立补偿模块GPU实现

获取卷绕模块已经得到了卷绕信息序列、相邻点的差值序列difference和卷绕点数量num,接下来需要建立补偿序列Offset如算法2。

算法2:建立补偿序列Offset

Input:difference、wrap、num

Output:Offset

__global__ void get_offset(float *difference,Wrap *wrap,float *Offset,int num)

{int tid = blockIdx.x * blockDim.x + threadIdx.x;

if(tid >= num) return;

for(int i = 0;i <= tid - 1;i++)

{sum = wrap[i].type + sum;}

A =(-1)* sum *(2 * CU_PI);

seg_start = int(wrap[tid - 1].id);

seg_end = int(wrap[tid].id);

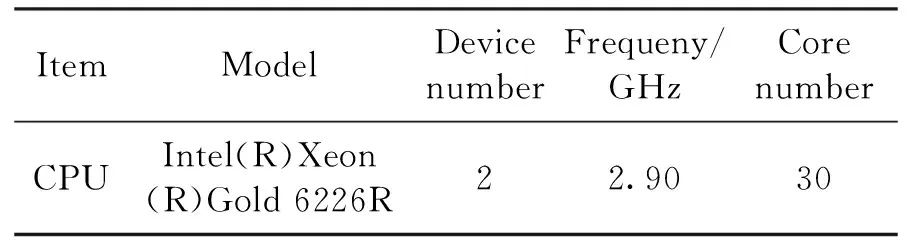
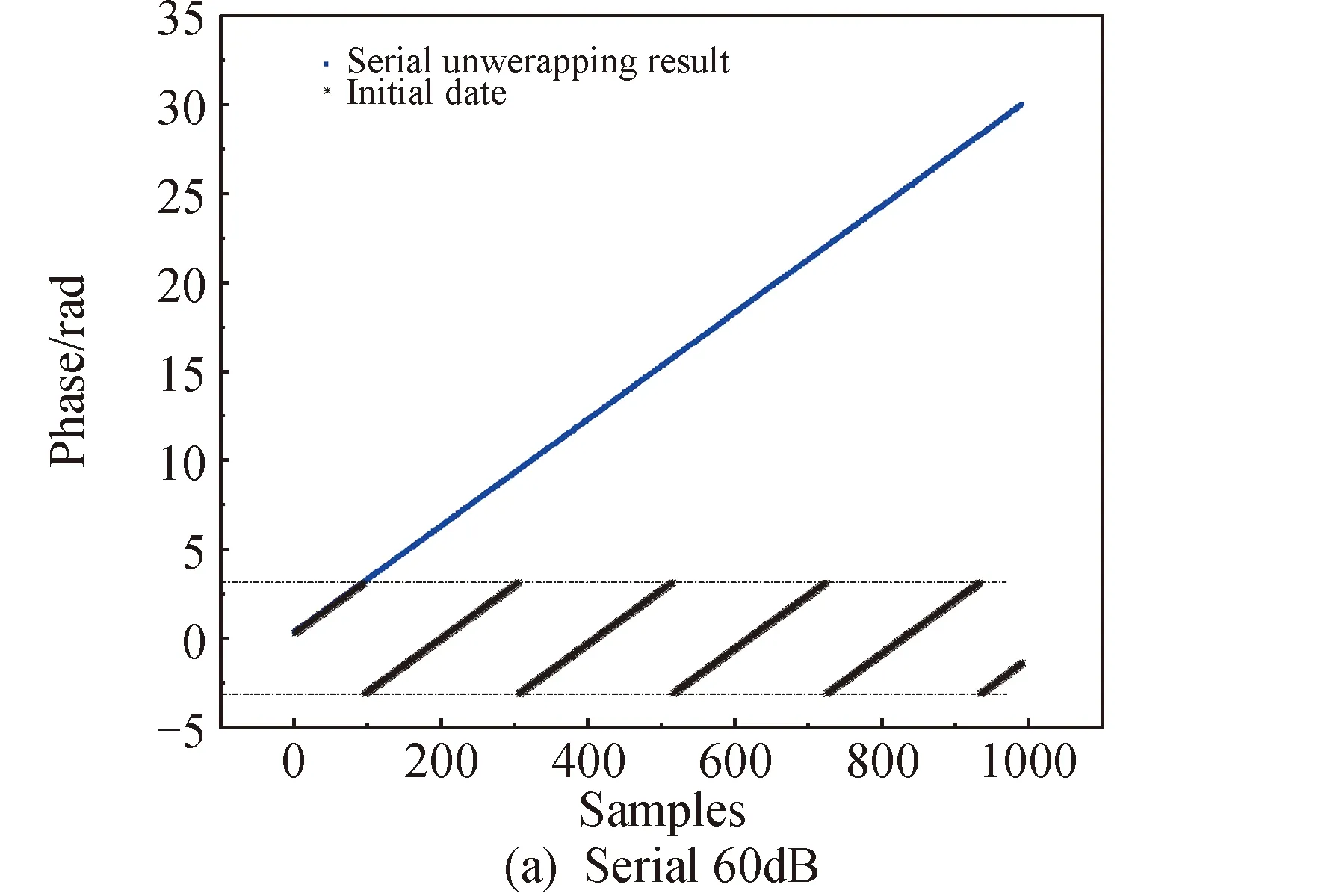
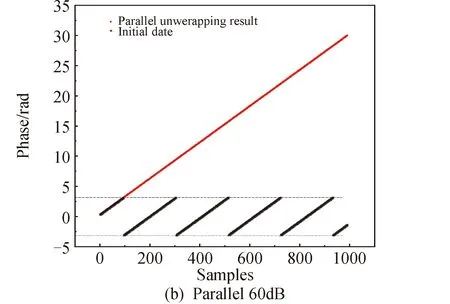
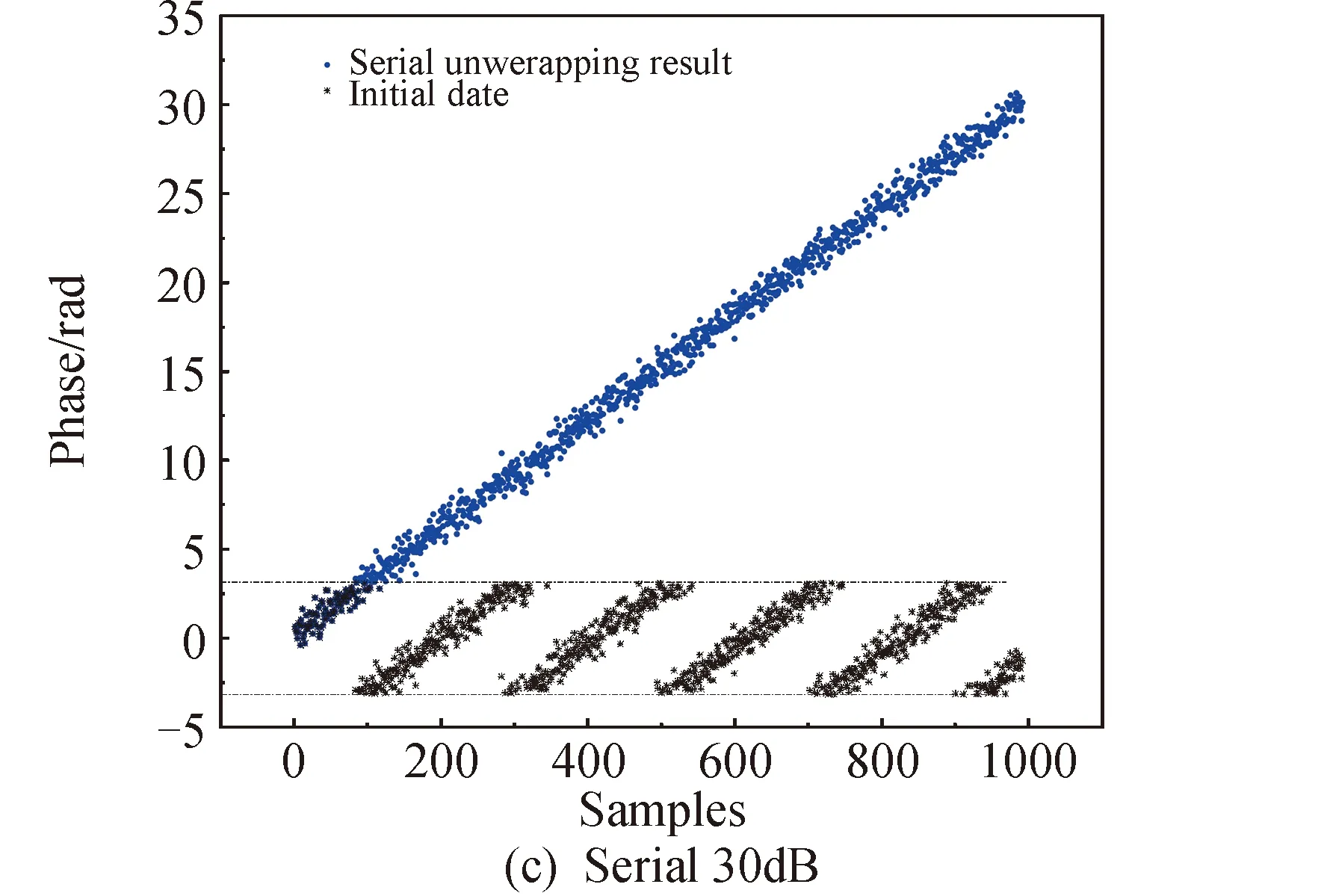
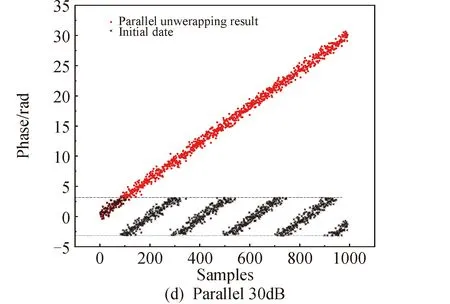
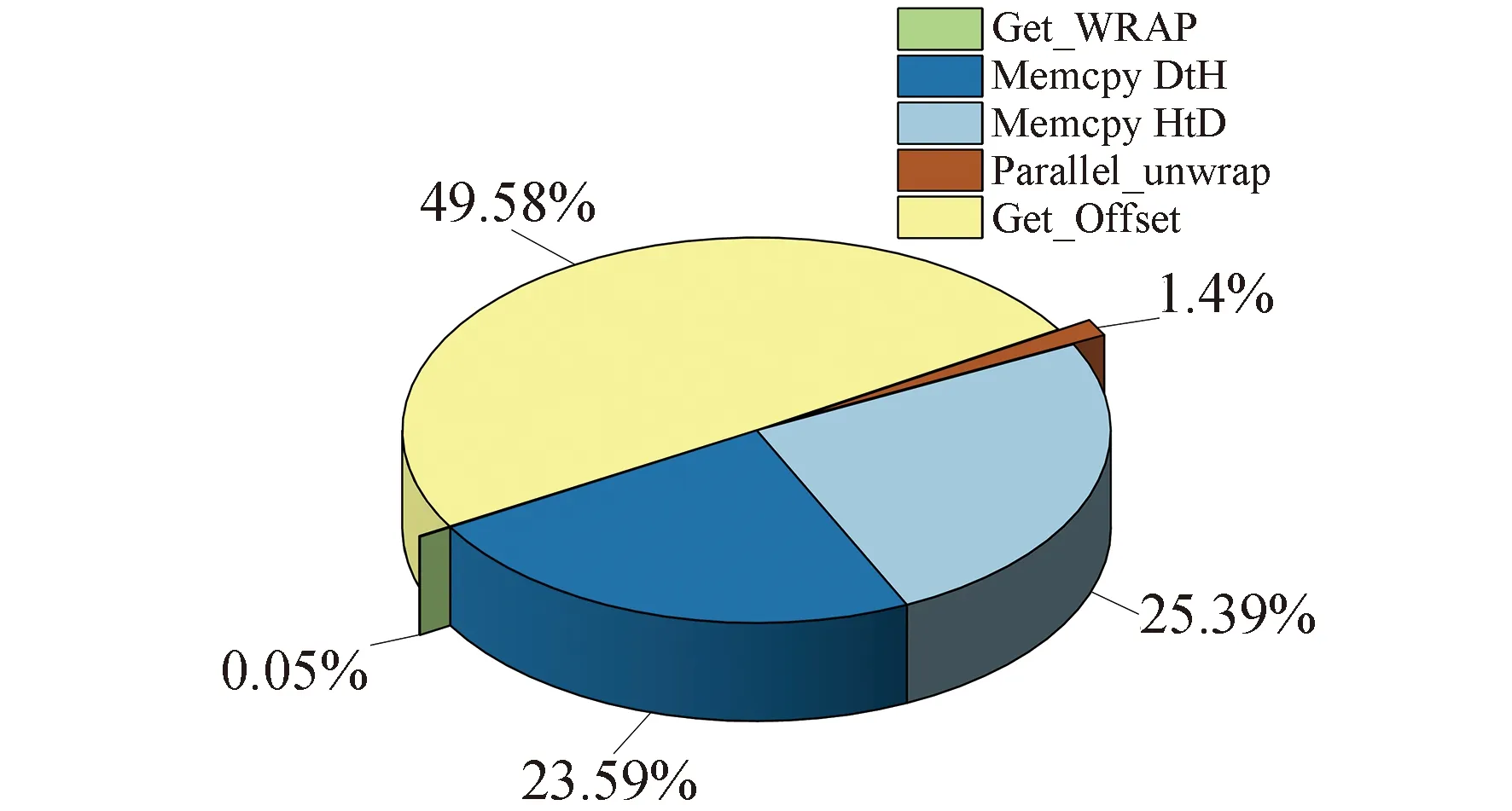
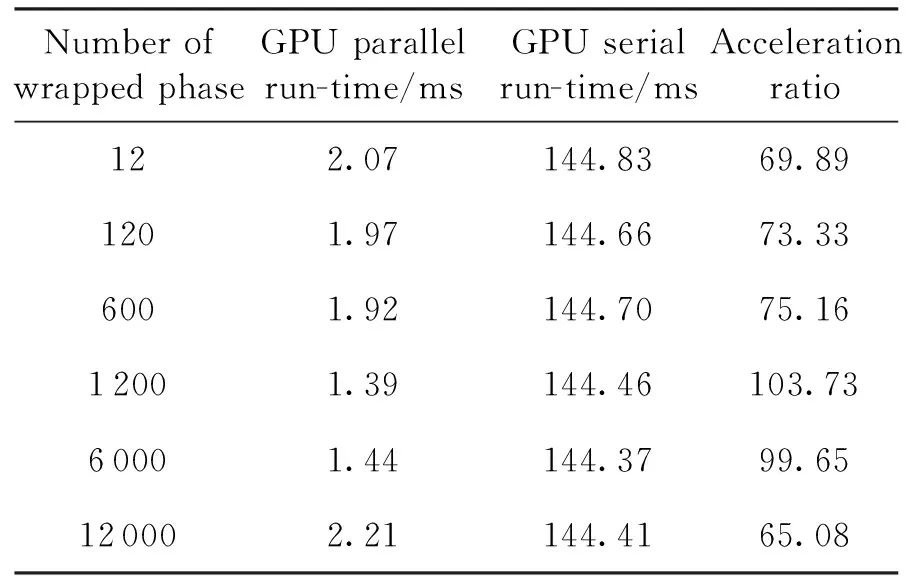
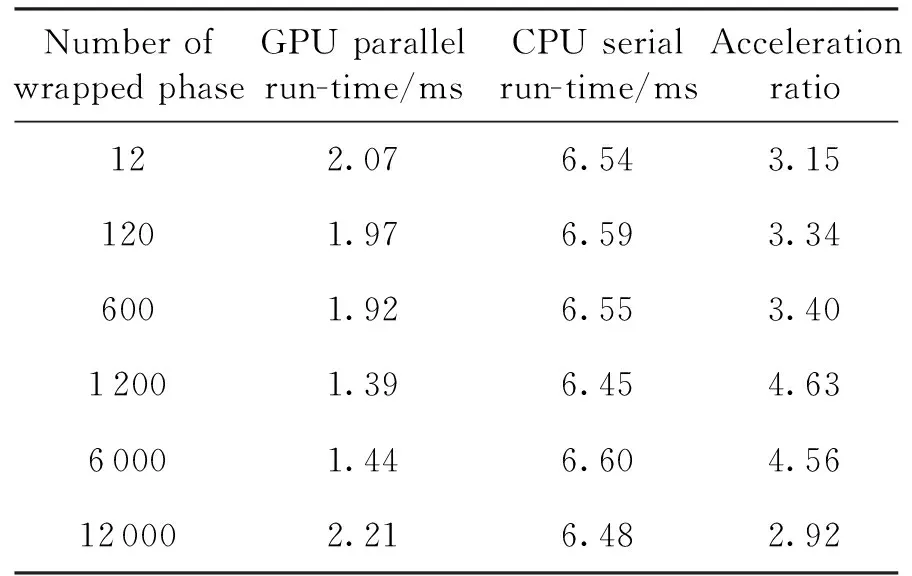
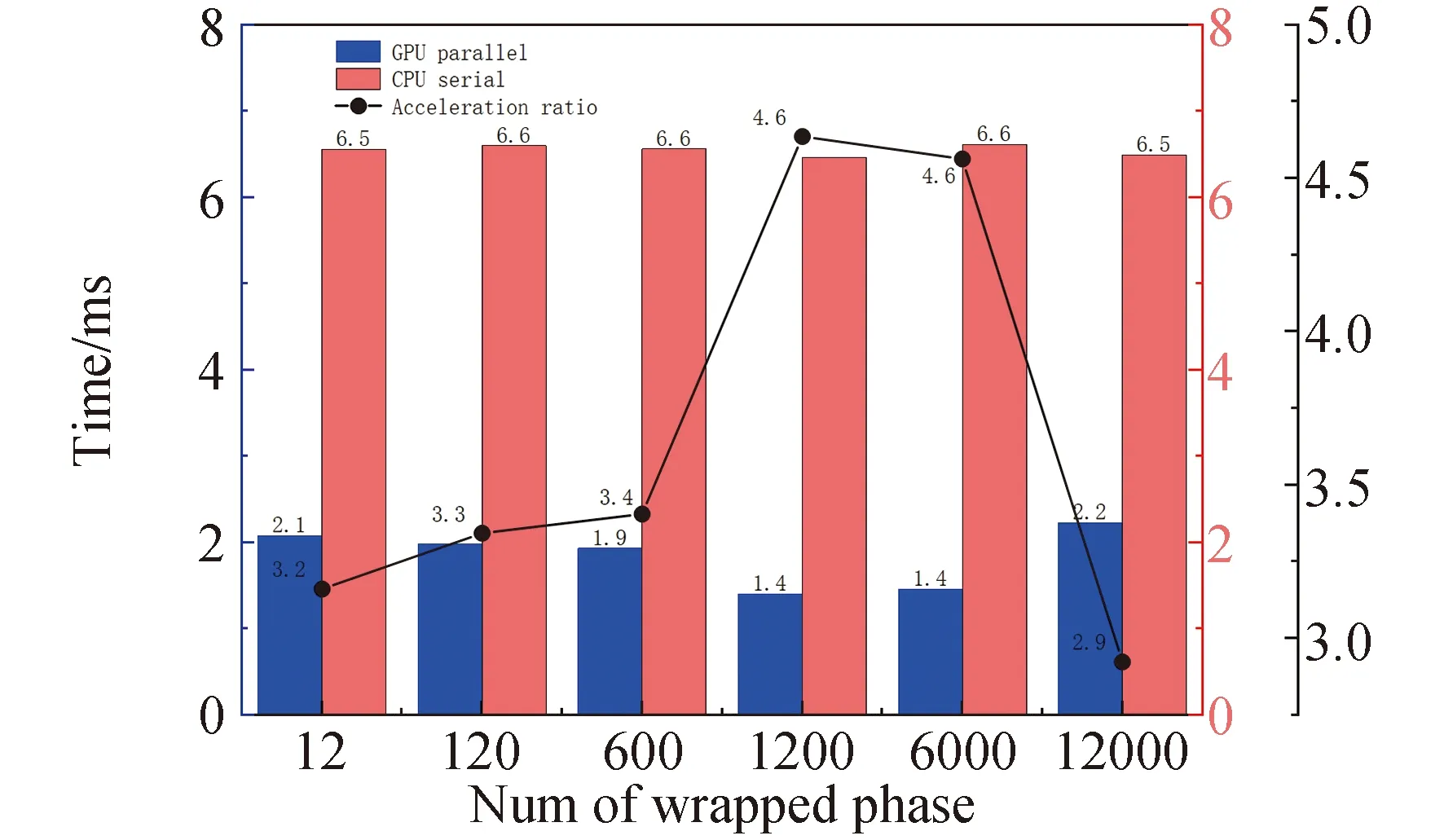
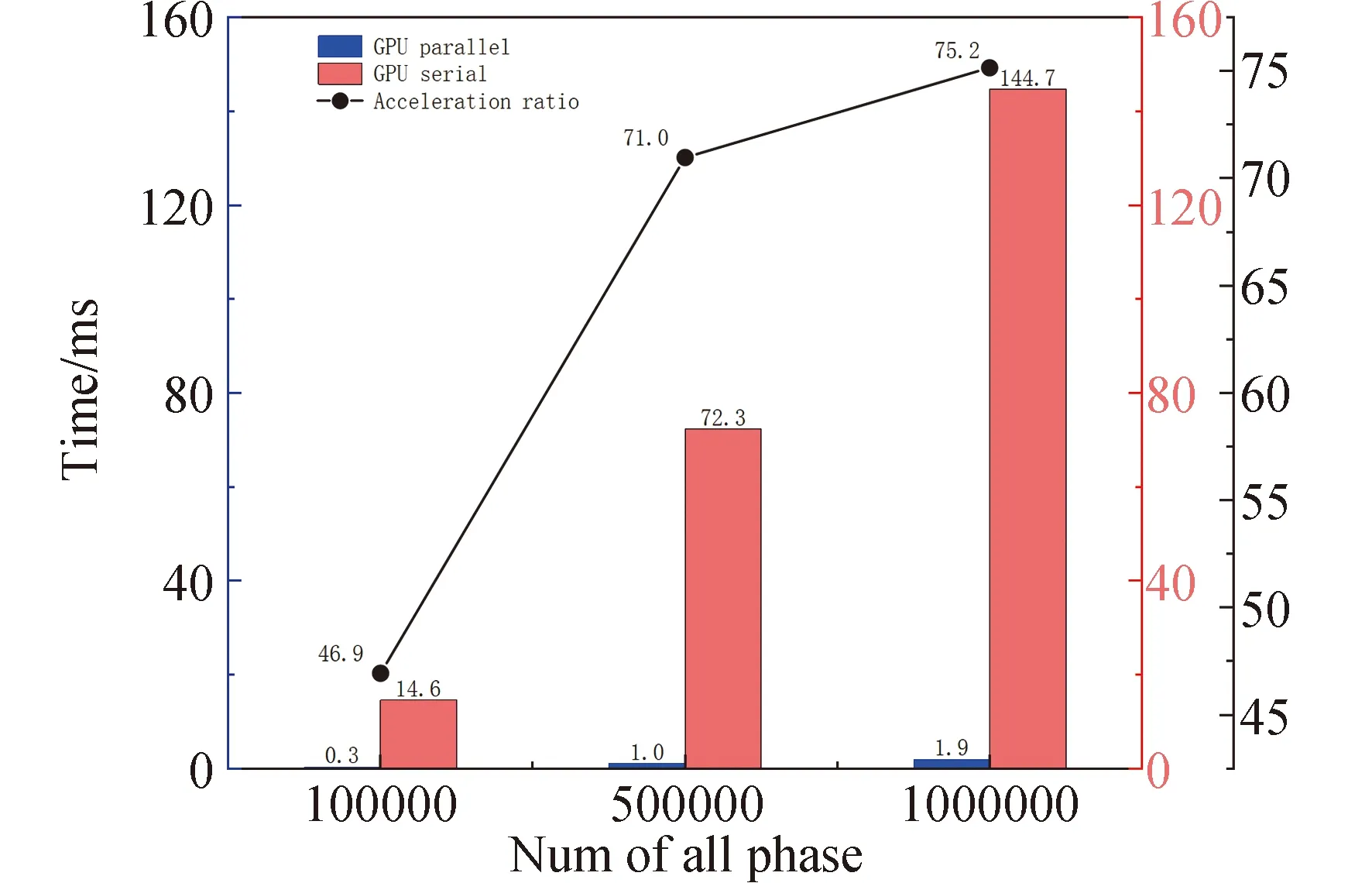
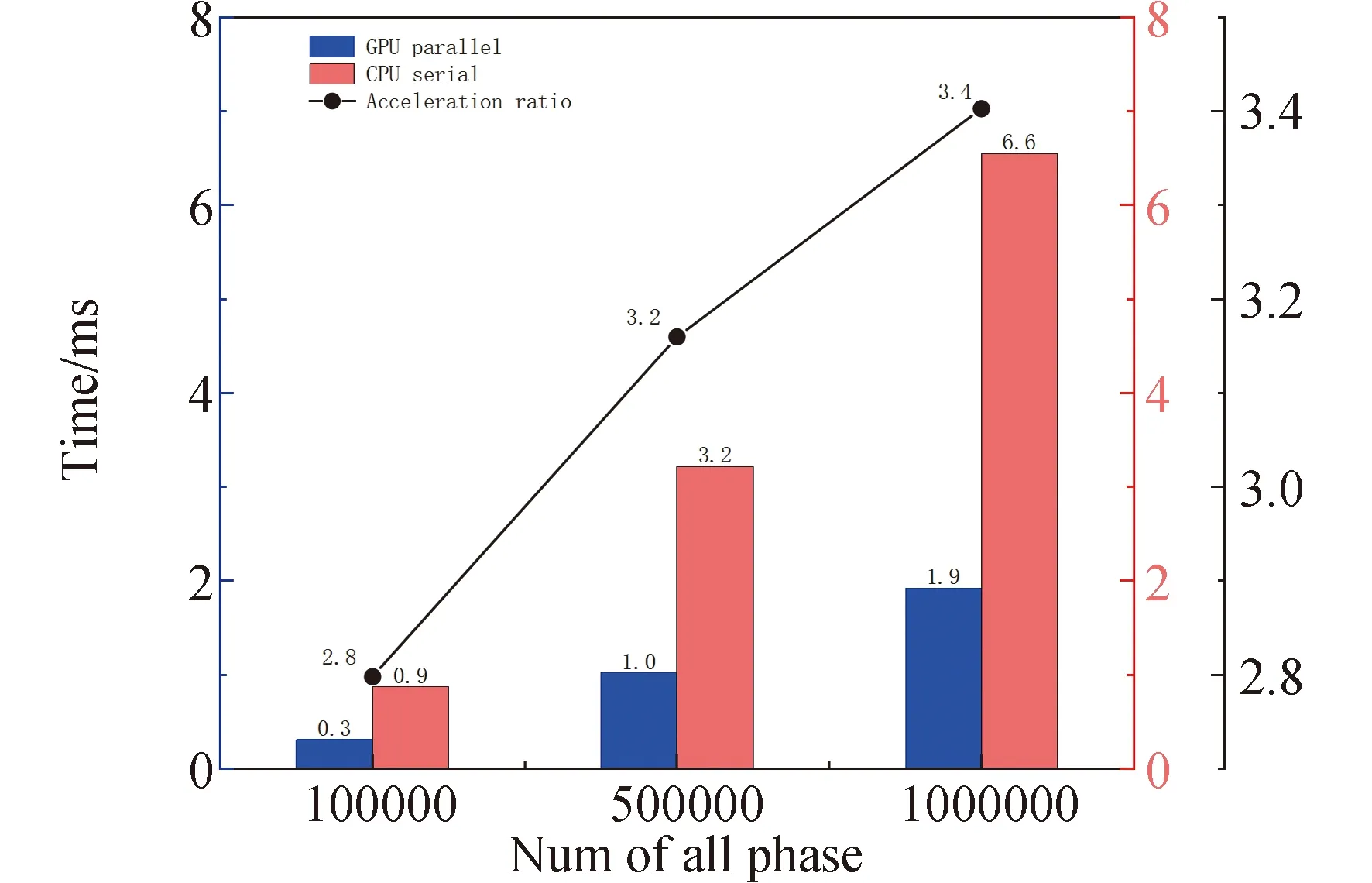
for(int i = seg_start - 1;i

Offset[i] = A;}

在本模块,调用num个线程,对应为各个分组,每个线程独立地计算该组的补偿值。根据公式(2)计算出每组的补偿值,并将每组的补偿值拓展到该组内的所有位置处,使得同一分组内的补偿值都相同,进而得到补偿序列Offset。

4.4 并行补偿模块GPU实现

并行解卷绕算法的最后一个模块就是并行补偿模块,利用补偿序列Offset对初始卷绕相位序列的所有值进行补偿。调用size个线程,size为原始相位序列的长度。每个线程独立地对每个值进行补偿,得到解卷绕之后的数据unwrap_data。

算法3:并行补偿

Input:wrap_data、Offset

Output:unwrap_data、size

__global__ void parallel_unwrap(double *wrap_data,float *unwrap_data,float *Offset,int size)

{int tid = blockIdx.x * blockDim.x + threadIdx.x;

if(tid >= size) return;

unwrap_data[tid] = wrap_data[tid] + Offset[tid];}

5 仿真验证与结果分析

在并行解卷绕仿真实验中,选用表1和表2所示的GPU和CPU仿真平台和具体仿真环境参数。

表1 GPU参数Table 1 Parameters of GPU

表2 CPU参数Table 2 Parameters of CPU

首先对并行解卷绕算法的正确性进行验证,仿真产生了1000点的卷绕相位序列,对序列进行加噪处理,并分别使用CPU串行解卷绕方法和GPU并行解卷绕方法进行运算,解卷绕结果如图6。

图6 解卷绕结果Fig.6 Result of phase unwrapping

从图中可以看出,在信噪比为30dB和60dB两种情况下,本文设计的GPU并行解卷绕算法与传统的CPU串行解卷绕算法结果一致,验证了GPU并行解卷绕方法的正确性。

之后利用NVIDIA提供的分析工具NVIDIA Nsight Systems软件统计了GPU并行解卷绕时间中CPU和GPU间的数据传输时间,以及GPU实际执行各自模块所占总执行时间的比例,具体时序图如图7。

图7 解卷绕算法运行时序Fig.7 Timeline of phase unwrapping

本文设计的基于GPU的并行相位解卷绕算法通过三个模块(获取卷绕模块、建立补偿模块、并行补偿模块)实现。统计了这些模块的耗时占比,除此之外,还统计了CPU和GPU间的数据传输时间占比,即Memcpy HtoD和Memcpy DtoH。GPU并行相位解卷绕算法的各模块耗时所占比例如图8所示,其中,所占比例最大的是建立补偿模块,达到了49.58%,接下来是CPU到GPU数据传输和GPU到CPU数据传输,分别达到了25.39%、23.59%。占用时间最少的是获取卷绕模块和并行补偿模块,分别为0.05%、1.4%。

图8 解卷绕算法各模块耗时占比Fig.8 Time consumption ratio of each module of phase unwrapping

之后对并行解卷绕的加速比进行仿真分析,考虑到在信号处理过程中,数据在GPU与CPU之间的传输耗时占比不可忽略,若信号处理系统通过GPU进行运算,则传回至CPU进行串行解卷绕需要耗费大量的传输时间,而在GPU中直接调用单核进行串行解卷绕是一种解决方法。因此本文仿真的对象分别为CPU串行解卷绕(CPU多线程)、GPU串行解卷绕(GPU单线程)、GPU并行解卷绕(GPU多线程)。

考虑到影响算法耗时的主要因素是原始相位数据量的大小和其中卷绕相位的数量。首先仿真产生6组原始相位数据,数据量固定为1000000,卷绕相位数量为12～12000不等。对GPU并行算法和GPU串行算法分别进行计时,得到表3所示中的耗时和加速比结果;对GPU并行算法和CPU串行算法分别进行计时,得到表4所示中的耗时和加速比结果。

表3 数据量固定情况下GPU并行算法较GPU串行算法加速效果对比Table 3 Comparison of acceleration effects between GPU parallel algorithm and GPU serial algorithm under fixed data volume

表4 数据量固定情况下GPU并行算法较CPU串行算法加速效果对比Table 4 Comparison of acceleration effects between GPU parallel algorithm and CPU serial algorithm under fixed data volume

图9为GPU并行解卷绕相比GPU串行解卷绕的加速效果对比图。图10为GPU并行解卷绕相比CPU串行解卷绕的加速效果对比图。

图10 加速效果对比2Fig.10 Comparison 2 of acceleration ratio

可以看到,在数据量固定时,随着卷绕相位数量增加,GPU并行解卷绕算法的耗时先升高后降低。分析原因如下:建立补偿序列模块为本算法中耗时占比最大的模块,在本模块,调用线程的数量为卷绕相位的数量,每个线程对应一个分组,每个线程独立地计算该组的补偿值。由此可知,本模块内线程并行的数量与卷绕相位的数量一致。因此,在数据量固定且卷绕相位小于6912时,卷绕相位数量越多,线程并行的数量也就越多,也就能更加充分地利用GPU的运算资源。此时,本模块总耗时与单个线程耗时的最大值相当,而线程并行的数量越多,单个线程处理的数据量就越少,耗时也就越短。而当卷绕相位大于6912时,线程数超过了设备的最大值,线程调度出现了拥塞,进而导致耗时增加。

下面考虑卷绕相位对算法耗时的影响,仿真产生3组原始相位数据,卷绕相位数量固定为600,每组的数据量为100000-1000000不等。对GPU并行算法和GPU串行算法分别进行计时,得到表5所示中的耗时和加速比结果;对GPU并行算法和CPU串行算法分别进行计时,得到表6所示中的耗时和加速比结果。

表5 卷绕相位数量固定情况下GPU并行算法较GPU串行算法加速效果对比Table 5 Comparison of acceleration effects between GPU parallel algorithm and GPU serial algorithm when the numder of winding phases is fixed

表6 卷绕相位数量固定情况下GPU并行算法较CPU串行算法加速效果对比Table 6 Comparison of acceleration effects between GPU parallel algorithm and CPU serial algorithm when the number of winding phases is fixed

在卷绕相位数量固定的情况下,图11为GPU并行解卷绕相比GPU串行解卷绕的加速效果对比图。图12为GPU并行解卷绕相比CPU串行解卷绕的加速效果对比图。

图11 加速效果对比3Fig.11 Comparison 3 of acceleration ratio

图12 加速效果对比4Fig.12 Comparison 4 of acceleration ratio

随着总数据量的增加,加速比呈现升高的趋势。数据量越大,GPU并行的优势越明显,这也印证了GPU确实适合大规模数据的实时处理。GPU并行解卷绕相比GPU串行解卷绕有63倍的加速比,GPU并行解卷绕相比CPU串行解卷绕约有3.5倍的加速比。出现两个数值不同的原因主要包括并发线程的数量和处理器的主频两方面。本文使用的GPU与CPU规格参数,GPU型号为NVIDIA TESLA A100,其时钟频率约为1.41GHz、最大核心数为6912。GPU并行算法与GPU串行算法都采用此GPU进行运算,二者唯一的区别就是线程并发的数量,GPU并行算法可同时并发成百上千个线程,而GPU串行算法则仅使用一个线程进行运算,因此加速比测试结果可达到文中的63倍。

GPU并行算法与CPU串行算法采用不同的处理器,CPU串行算法采用两块Intel(R)Xeon(R)Gold 6226R处理器,虽然其线程并发的最大数量为32个,但其主频可达到2.9GHz。综合线程并发数与主频两个因素,CPU串行算法的线程并发数与主频都高于GPU串行算法,因此,GPU并行算法相比CPU串行算法无法达到63倍(GPU串行算法)的加速比,经过多组实验测试只能达到3.5倍加速比。

6 结论

针对大量数据串行相位解卷绕实时性较差的问题,分析了算法并行的可行性并设计了基于GPU的并行相位解卷绕算法。通过获取卷绕模块、建立补偿模块、并行补偿模块实现并行解卷绕。并利用线程并行、GPU并行、SIMD、原子操作等方法对算法进行优化。

本文中算法在不同信噪比条件下与传统串行解卷绕方法结果一致。证明了本文中算法在GPU平台下实现的正确性。之后对GPU并行解卷绕、GPU串行解卷绕、CPU串行解卷绕三种算法的实时处理能力进行了对比。实验表明,基于GPU的并行解卷绕算法相比CPU串行解卷绕算法有约3.5倍的加速比,相比GPU串行解卷绕算法有63倍的加速比。因此,本文设计的基于GPU的并行相位解卷绕算法对深空天线组阵信号合成、行星探测任务的变轨、捕获等航天任务具有重要的工程意义。