宽带高灵敏水声换能器的研究

苏晋涛,王宏伟

(北京信息科技大学 理学院,北京 海淀 100192)

0 引言

声纳被誉为海中“顺风耳”和“千里眼”,被广泛应用于海洋探测和水声通信。有“水声设备耳目”之称的水声换能器则是声纳的关键部分[1],是水下通讯、探测的重要工具。其中,将电能转换成机械能,进而再转换为声能的器件叫做发射换能器,用于发射声波;将声能转换成机械能,进而再转换成电能用于接收声波的换能器叫做水听器。

换能器具有多种分类[2]。按照换能机理和物理效应,水声换能器可分为压电换能器、电致伸缩和磁致伸缩换能器、可变磁阻换能器和电动原理换能器;按照应用以及工作频段,水声换能器可分为低频换能器、中频换能器和高频换能器[3];按照工作振动模式,水声换能器可分为厚度振动换能器、剪切振动换能器及弯曲振动换能器等。

压电陶瓷作为换能器研制和发展的关键材料[4],改善压电陶瓷结构可以极大地提升换能器的性能[5]。研究人员在换能器有源材料选择方面进行了大量的研究工作,目前常见的压电材料有1-1、1-2,1-3,2-2,1-3-2等[6]。单金属板空气柱型压电陶瓷阵列结构[7-8]是将压电陶瓷的厚度振动变为压电小柱的长度伸缩,与现有的压电材料相比,其有效机电耦合系数和接收灵敏度有了较大提升。

对于中高频换能器的研究,目前主要集中在拓展换能器的工作带宽,提高换能器的接收灵敏度和发送电压响应[9],以便使换能器接收和发射更多的信号,同时提升换能器对于水下微弱信号的探测能力[10]。为实现带宽拓展的目的,本文依据多模耦合原理设计了一种“金字塔”型换能器结构。这种结构由4层不同厚度的敏感元件组成,其优点在于通过多层不同厚度的敏感元件嵌套叠加,在各自下降-3 dB频率点处重合时,可以有效拓展带宽。本文设计的换能器发射接收带宽均在100 kHz以上,与同类型换能器带宽(一般在20～60 kHz)相比有较大提升。通过在切割的压电小柱阵列间不填加聚合物的方式,实现了压电小柱的长度伸缩振动;同时在压电阵列上方覆盖硬质金属板,从而增大输出感应电压,提高接收灵敏度(多数约为-200 dB)。

1 宽带高灵敏换能器结构

通过改变材料的振动模态可以有效提高压电材料的机电耦合系数。为了验证高灵敏压电材料提升换能器灵敏度的性能,本文制作了“BPM”型(陶瓷基底、压电陶瓷住、金属板)压电材料的单层敏感元件换能器,确定了制作高灵敏宽带换能器的有源材料。图1为BPM改进结构的压电材料。

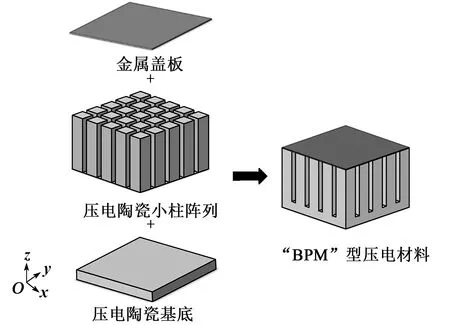
图1 “BPM”型压电材料结构

依据多模耦合技术原理,设计了“金字塔”型换能器敏感元件结构如图2所示。

图2 “金字塔”型换能器敏感元件结构示意图

2 高灵敏压电材料理论分析

换能器工作时,通过机械状态方程可以描述系统的力与振速之间的关系;在电学中,电路系统的振动特性是通过电路状态方程进行描述。压电材料产生的压电效应使机械和电路相互耦合,故可利用机械状态方程和电路状态方程求解换能器振子的机电等效图,并用等效图求解影响换能器性能指标的参数。

“BPM”型压电材料由压电陶瓷基底、周期排列的压电小柱阵列和金属板构成。为了简化分析过程,选取如图3所示的“BPM”型压电材料周期单元进行理论分析研究。

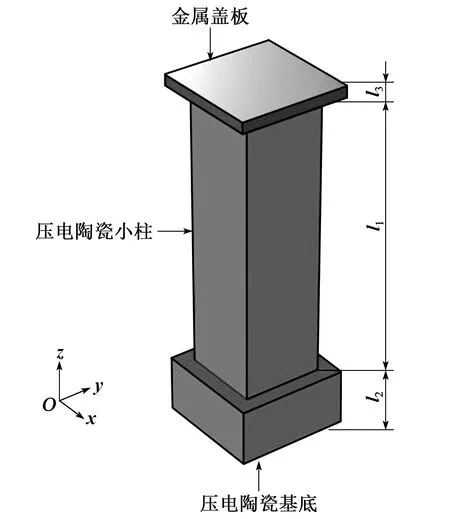
图3 “BPM”型压电材料周期单元模型

设压电小柱的长度为l1,横截面积为Sz,压电陶瓷小柱的长度平行于z轴并沿z轴极化,电极面加在压电小柱的上下两面。此时电场方向沿z轴方向,忽略边界效应,所以视作仅有z轴方向的电场强度不为0,即E3≠0,E1=0,E2=0。

对于“BPM”型压电材料的单个压电小柱,其长度尺寸可与声波波长相比,而其横截面积的线度远小于波长,可视为横截面处无声波传输,则有T1=T2=T4=T5=T6=0,T3≠0。

根据上述分析,选用电位移和应力作为变量,g-型压电方程可简化为

(1)

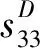
由式(1)的第一式可得纵向正应力T3为

(2)

将式(2)代入式(1)中的第二式,得到纵向电场分量E3为

(3)

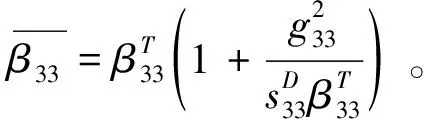
由式(3)积分可得压电陶瓷小柱两端电压:

(4)

式中ζ1和ζ2分别为压电陶瓷小柱沿Z方向底端面(z=l2)和顶端面(z=l1+l2)的位移。

由式(3)可得纵向电位移矢量D3为

(5)

由式(5)可得压电陶瓷小柱的电路状态方程为

I1=jωQ3=jωSzD3=jωC0V1-n1(v2+v1)

(6)

在弹性力学中,压电陶瓷的运动方程根据边界条件可化简为

(7)

将式(2)代入式(7)得

(8)

(9)

当施加简谐激励时,式(9)化简为

(10)

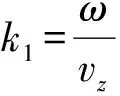
根据压电陶瓷小柱两端的边界条件ζz=0=ζ1,ζz=l1=ζ2,可以求出式(10)的解:

(11)

结合力的分布与应力、横截面积的关系,代入式(2)得

(12)

由于压电陶瓷小柱上下端面受到的力应该与外力平衡,可得单个压电小柱的机械振动方程为

(13)

“BPM”型压电材料的中间部分是由m个压电陶瓷小柱构成的阵列,故压电陶瓷小柱阵列上端面受到的力F1=mFu,下表面受到的力F2=mFl。压电陶瓷小柱阵列的机械振动方程为

(14)

根据电路状态方程机械振动方程,可得“BPM”型压电陶瓷小柱阵列的机电等效图如图4所示。

图4 压电陶瓷阵列的机电等效图

由于压电陶瓷基底和压电陶瓷小柱完全粘接,可认为压电陶瓷小柱底端面和压电陶瓷基底顶端面振速(v1)相同。设压电陶瓷基底厚度为l2,横截面积为Sx,厚度方向平行于z轴,且沿厚度方向极化陶瓷,压电陶瓷基底上下端面为电极面,压电陶瓷基底厚度可与波长相比,横向尺寸远大于波长。此时厚度振动的谐振频率远大于平面轮廓的振动频率,即压电陶瓷基底是横向截止的,应变S3≠0,S1=S2=S4=S5=S6=0。由于电场方向平行于z轴方向,且电极面垂直于z轴,此时无漏电位移通量,即D1=0,D2=0,D3≠0。

根据上述分析,选用电位移和应变作为变量,h-型压电方程可简化为

(15)

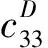
由式(15)第二式可得应变分量D3:

(16)

由于压电陶瓷晶体内无自由电荷,即

(17)

且

(18)

式(16)可化简为

(19)

对式(19)积分可得

(20)

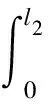
(21)

式中ζ1和ζ3分别为压电陶瓷基底沿Z方向顶端面(z=l2)和底端面(z=0)的位移。此时

(22)

将式(19)代入式(16),得到电位移矢量D3:

(23)

I=jωSxD3=jωC0V2-n2(v3+v1)

(24)

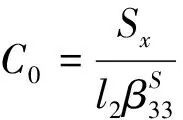
根据边界条件,运动方程(7)可化简为

(25)

将式(15)第一式、式(17)、(18)代入式(22),可得

(26)

对于简谐激励,运动方程(23)可表示为

(27)

(28)

力的分布为应力乘以横截面积,由F=TSx和式(15)第一式,并考虑压电陶瓷基底两端的力应与外力平衡,得到

(29)

式中F3和F4分别为压电陶瓷基底底端面(z=0)和顶端面(z=l2)的外力。

将式(23)、(29)代入式(30),得到压电陶瓷基底的机械振动方程:

(30)

由压电陶瓷基底电路状态方程和压电陶瓷基底机械振动方程得到压电陶瓷基底的机电等效图如图5所示。

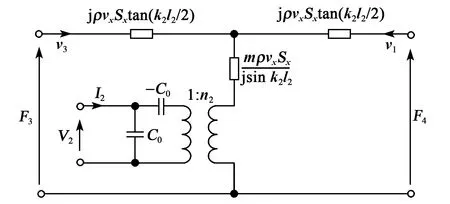
图5 压电陶基底的机电等效图

“BPM”型压电材料的金属盖板和压电陶瓷小柱完全粘接,可认为压电陶瓷小柱顶端面和金属盖板底端面振速(v2)相同。设金属盖板厚度为l3,横截面积为Sy,密度为ρ0,其厚度可与波长相比,横向尺寸远大于波长,可认为金属盖板的振动模态是无限大平板纵振动。其机械振动方程推导过程与压电陶瓷基底相似,只需压电常数为0,即可得到金属盖板的机械振动方程为

(31)

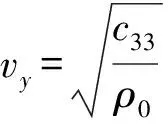
图6 金属盖板等效机械图

压电陶瓷基底的上端面与压电小柱阵列的下端面沿z轴方向连接,压电陶瓷小柱阵列的上端面与金属盖板的下端面沿z轴方向连接,因此认为端面处的应力分布与运动状态一致。将声场作用力F6和F3分别换成金属盖板前辐射声阻抗Zs和压电陶瓷基底后的空气等材料的阻抗Zb,即可得到“BPM”型压电材料作为敏感元件在空气中振动时的机电等效图。如图7所示,其中1部分为压电陶瓷基底厚度振动机电等效图,2部分为压电陶瓷小柱阵列长度伸缩振动机电等效图,3部分为金属盖板板纵振动的等效机械图。

图7 “BPM”型压电材料机电等效图

当敏感元件在空气中振动时,Zs=0。为了分析计算的简便,根据电-力类比关系将“BPM”型压电材料作为敏感元件,其在空气中振动时的机电等效图简化为图8所示。

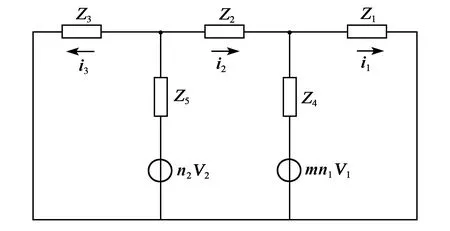
图8 化简后等效图

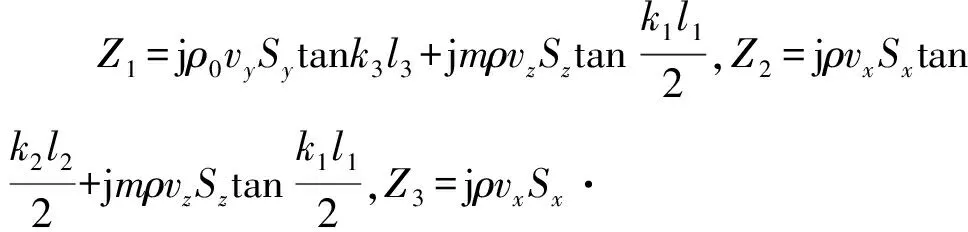
(32)

解得辐射面的振速为

(33)

式中R1=(Z3+Z5)Z4。

式(29)反映了“BPM”压电材料各部分尺寸与共振频率之间的关系。以压电陶瓷PZT-5A和金属薄板材料铜为例,计算分析了敏感元件的谐振频率随压电小柱长度的变化趋势。分别将PZT-5A和铜的相关材料参数代入式(33),得到如图9所示的谐振频率随各尺寸变化的趋势图。

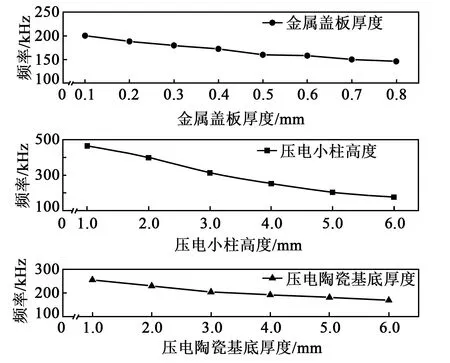
图9 “BPM”型压电材料谐振频率随各尺寸变化趋势

3 敏感元件有限元分析

3.1 不同压电材料有效机电耦合系数的对比

有限元仿真软件对“BPM”型压电材料进行了谐响应分析,研究了材料的各尺寸参数对谐振频率以及有效机电耦合系数的影响,建立了换能器敏感元件模型,并进行了水下电声性能的仿真。

有效机电耦合系数(ke)是表征压电敏感元件能量转换强弱的量,反映了压电敏感元件的性能,可表述为

(34)

式中:fs为压电振子的谐振频率;fp为压电振子的反谐振频率。

为了对比1-3型压电复合材料、1-3-2型压电复合材料、“BPM”型压电材料敏感元件的有效机电耦合系数,分别建立了相同几何尺寸的敏感元件模型。通过有限元仿真得到各敏感元件的谐振频率和反谐振频率,并计算了各自的有效机电耦合系数。其中,各敏感元件的纵向长度均为5.7 mm,1-3型压电复合材料敏感元件的压电小柱宽度为1.6 mm;1-3-2型压电复合材料敏感元件的基底为1 mm,压电小柱高度为4.5 mm,压电小柱的宽度为1.6 mm;“BPM”型压电材料敏感元件的金属板厚度为1 mm,基底厚度为1 mm,压电小柱高度为4.5 mm。各类型敏感元件有限元模型和谐振频率下敏感元件位移场分布图如图10所示,仿真结果和有效机电耦合系数对比结果如表1所示。

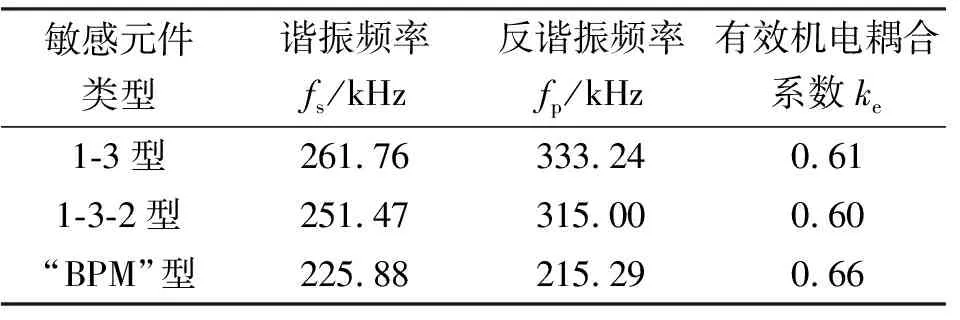
表1 不同类型敏感元件有效机电耦合系数

图10 有限元仿真模型和谐振频率下位移场分布图

由表1可见,“BPM”型压电材料敏感元件的有效机电耦合系数最大,与同几何尺寸的1-3型压电复合材料和1-3-2型压电复合材相比,“BPM”型压电材料敏感元件的谐振频率有所下降,有效机电耦合系数提高了约10%,表明这种改进型的压电材料具有较好的压电性能。

3.2 单元参数对“BPM”型压电材料的影响

根据“BPM”型压电材料的结构可知,“BPM”型压电材料由金属盖板、压电陶瓷小柱阵列和压电陶瓷基底沿z方向串联而成。金属盖板和压电陶瓷基底的厚度,以及压电小柱阵列的高度会影响“BPM”型压电材料的性能。为了进一步研究各单元参数对材料性能的影响,利用有限元仿真软件仿真计算了各单元参数对材料谐振频率和有效机电耦合系数的影响。

3.2.1 金属盖板厚度对材料性能的影响

仿真过程中,在保证压电陶瓷基底厚度和压电陶瓷小柱高度恒定的情况下,改变金属盖板的厚度,其谐振频率、反谐振频率以及有效机电耦合系数的变化曲线如图11所示。不同厚度敏感元件的位移场分布图如12所示。

图11 金属板厚度对“BPM”型压电材料谐振频率和有效机电耦合系数的影响

由图11可见,“BPM”型压电材料的谐振频率随金属盖板厚度的增加而逐渐降低,这与理论分析的结果相吻合,其有效机电耦合系数基本保持在0.66～0.67。由图12可见,随着金属盖板厚度的增加,其振动位移逐渐减弱,表明材料辐射声波的能力减弱。由图12(a)可知,当金属盖板厚度为0.1 mm时,铜板自身振动幅度较大,应力放大效果减弱,考虑到传声效应,金属盖板应保证尽量薄且硬。因此,金属盖板的厚度选择0.2 mm为宜。

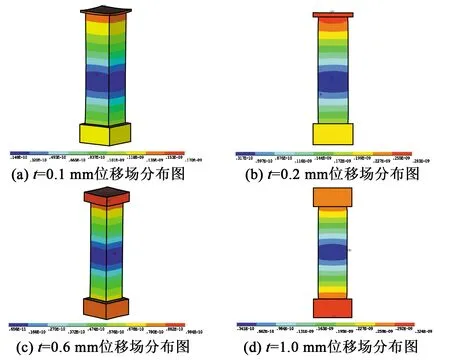
图12 不同厚度金属盖板谐振频率处位移场分布图的影响

3.2.2 压电陶瓷基底对材料性能的影响

在保证金属盖板厚度和压电陶瓷小柱高度恒定不变的条件下,改变压电陶瓷基底的厚度,其谐振频率、反谐振频率以及有效机电耦合系数的变化曲线如13所示。谐振频率处导纳幅值变化曲线如14所示。

由图13、14可见,随着压电陶瓷基底厚度逐渐增加,压电陶瓷基底的厚度振动模态逐渐占据主导地位,“BPM”型压电材料的谐振频率逐渐降低,压电材料敏感元件的有效机电耦合系数也逐渐降低,谐振频率处的导纳值随之降低,表明材料辐射声波的能力减弱。考虑到压电陶瓷基底太薄易导致材料断裂,故压电陶瓷基底的厚度宜选择为1.0 mm。

图13 “BPM”谐振频率和有效机电耦合系数

图14 不同基底厚度谐振频率处导纳幅值

3.2.3 压电陶瓷小柱高度对材料性能的影响

在保证压电陶瓷基底厚度和金属盖板厚度恒定的情况下,改变压电陶瓷小柱的高度,其谐振频率和反谐振频率的变化曲线如图15所示,压电敏感元件的有效机电耦合系数和谐振频率处的导纳幅值变化曲线如图16所示。

图15 “BPM”型压电材料谐振频率随压电小柱高度变化曲线

图16 压电小柱高度对“BPM”型敏感元件性能的影响

由图15可知,“BPM”型压电材料的谐振频率随压电小柱高度增加而逐渐降低。由图16可知,随着压电小柱高度增加,敏感元件的有效机电耦合系数也随之升高,这表明压电小柱越长,越能激发长度伸缩振动模态,但随着压电小柱高度增加,其谐振频率处的导纳幅值也在降低,因此,压电小柱的高度不宜过高。

4 “金字塔”结构宽带高灵敏换能器的研制与性能测试

4.1 制作

结合理论和仿真可得,4层嵌套式换能器敏感元件材料厚度分别为4.2 mm,4.7 mm,5.2 mm,5.7 mm,制作得到的不同厚度敏感元件如图17所示。

图17 不同厚度的“BPM”型压电敏感元件

制作的“BPM”型敏感元件是基底厚度均为1 mm,金属盖板的厚度均为0.2 mm,单个压电陶瓷小柱的尺寸为1.5 mm×1.5 mm,相邻两个压电小柱之间的距离为0.5 mm。图17中厚5.7 mm的“BPM”型敏感元件编号为①,尺寸为39.5 mm×39.5 mm;厚5.2 mm的“BPM”型敏感元件共4块,编号为②和③的敏感元件尺寸为39.5 mm×9.5 mm,编号为④和⑤的敏感元件尺寸为59.5 mm×9.5 mm;厚4.7 mm的敏感元件共4块,编号为⑥和⑦的敏感元件尺寸为59.5 mm×9.5 mm,编号为⑧和⑨的敏感元件尺寸为79.5 mm×9.5 mm;厚4.2 mm的敏感元件共4块,编号为⑩和的敏感元件尺寸为79.5 mm×9.5 mm,编号为和的敏感元件尺寸为99.5 mm×9.5 mm。将同一厚度的敏感元件使用粘接剂粘接,得到如图18所示的4层不同厚度的敏感元件。

图18 粘接后的不同厚度敏感元件

将4层不同厚度的敏感元件沿轴向嵌套粘接,得到辐射面齐平的“金字塔”结构敏感元件如图19所示。敏感元件的尺寸为99.5 mm×99.5 mm。使用万用表测试嵌套式敏感元件,确保相同厚度的敏感元件之间电连通,但不同厚度的敏感元件之间进行电隔离。

图19 “金字塔”结构敏感元件

4.2 “金字塔”结构换能器敏感元件性能测试

4.2.1 水中电导曲线

分别测试不同厚度的敏感元件以及换能器整体的电导曲线,其结果如图20所示。由于水中损耗较大,不同厚度敏感元件的谐振频率较空气中有所下降,换能器的电导峰值降低,不同厚度的敏感元件之间产生明显耦合。

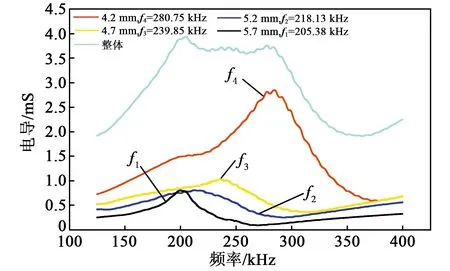
图20 换能器在水中的电导曲线

4.2.2 发射电压响应级曲线

换能器发射电压响应级曲线如图21所示。由图可知,换能器在谐振频率为210 kHz时,发送电压响应达到峰值189.2 dB,-3 dB带宽为170 kHz,频带范围为200～360 kHz。根据测试结果可知,使用频带叠加的方式可以有效拓展换能器带宽。

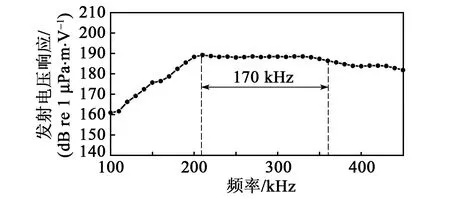
图21 发送电压响应曲线

4.2.3 接收灵敏度曲线

换能器接收灵敏度曲线如图22所示。由图可知,制作的换能器最大接收灵敏度为-173.7 dB,换能器接收灵敏度曲线整体较平坦,接收带宽为110 kHz,达到高灵敏的设计目的。以此证明了“BPM”型压电材料可以提高换能器的接收灵敏度。

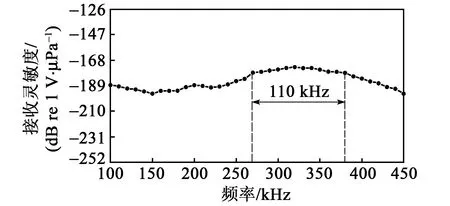
图22 接收灵敏度曲线

4.2.4 指向性测试

制作的换能器的整体指向性图如图23所示。换能器的-6 dB指向性开角为8.1°。

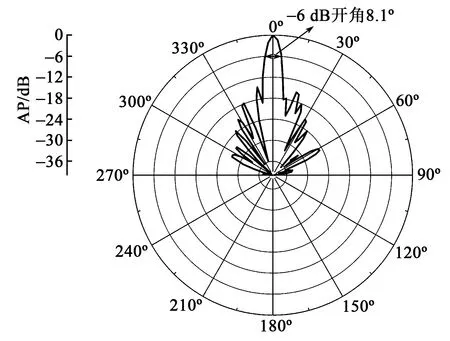
图23 换能器波束指向性开角

5 结束语

本文提出了一种改进的1-3型压电复合材料,即“BPM”型压电材料。相比于现有的换能器,本文研究在材料方面改变了压电陶瓷的结构,有效机电耦合系数和灵敏度得到提升;在结构方面,不同厚度的压电材料按“金字塔”型结构多层排列,通过多模耦合原理提升了换能器的整体带宽,进而实现了宽带和高灵敏性能。