压电微纳定位平台自适应陷波滤波在线谐振抑制

王雯雯,赖磊捷

(上海工程技术大学 机械与汽车工程学院,上海 201620)

0 引言

微纳米定位技术在纳米光刻、生物显微操作和超精密制造与测量等领域中有着广泛而重要的应用[1-2]。压电陶瓷驱动器具有刚度高、分辨率高、精度高、响应速度快等优点。结合柔性机构具有的无摩擦、无间隙、无需润滑、分辨率高等优点,压电驱动的柔性微纳米定位平台在微纳米定位技术中具有重要地位[3-4]。

压电驱动柔性微纳米定位平台使用柔性机构弹性变形来实现微位移传动,通常呈现较低的阻尼比,在跟踪同频带内的高速运动轨迹时易产生自激振荡,影响系统控制性能[5-6]。为消除柔性机构低阻尼谐振的影响,基于反馈控制的主动振动控制策略是目前常见的方法,这类方法通过改变系统零极点分布来增加其阻尼比,进而达到抑制谐振的目的。例如英国阿伯丁大学Aphale等通过优化设计分数阶积分谐振控制器(IRC)来提升系统的闭环控制带宽,增加了系统的跟踪性能[7]。上海交通大学Li等设计了一种位置/速度/加速度正反馈的阻尼控制器,以此获得更大的阻尼比[8]。但这类方法的缺点是在设计过程中需要精确获得系统模型。国内外学者还提出了基于陷波滤波器或系统逆模型的方法[9-10],通过零极点抵消来消除低阻尼谐振的影响,但此方法对系统模型比较敏感,负载和环境等因素的变化引起的模型误差容易导致控制鲁棒性差,甚至系统不稳定。由以上分析可见,如何在各类谐振抑制控制方法中消除对被控对象精确数学模型的依赖性,有效提升谐振控制器鲁棒性和自适应性能是亟待解决的问题。

为解决上述问题,针对压电驱动柔性微纳定位平台的低阻尼谐振问题,本文设计了可以有效抑制平台谐振的自适应陷波滤波器。通过实时检测谐振频率的动态变化来在线更新陷波滤波器参数,进而可以实现自适应的谐振抑制功能。首先搭建了基于压电陶瓷驱动器与桥式放大柔性机构的微纳定位平台及其实验系统。其次,基于FFT方法设计了谐振频率在线提取算法,并以此对陷波滤波器中心频率、深度和宽度等参数进行自适应调整,进而抑制系统的谐振现象。最后,利用所设计的微纳定位平台和自适应陷波滤波器进行轨迹跟踪实验,以此验证了谐振抑制算法的可行性、有效性。

1 压电微纳定位平台及其动力学模型

压电驱动微纳定位平台实验系统由压电陶瓷驱动器PAL40VS12(行程为38 μm,刚度为25 N/μm),压电控制器PDS21(输入0～+10 V对应输出0～+120 V),电容传感器(0～10 V对应0～200 μm),数据采集卡PCI-6221以及柔性机构等组成,各组成部分连接关系如图1所示。柔性机构采用复合桥式放大机构来实现对压电驱动器输出位移的有效放大,输出端采用平行四边形机构来减少寄生位移。

图1 微纳定位平台实验系统

压电驱动柔性微纳定位平台中,平行四边形柔性机构看成刚度为ks的弹簧和阻尼系数为cs的阻尼器,含桥式放大的压电陶瓷驱动器也可看作刚度为kAP的弹簧和阻尼系数为cAP的阻尼器,等效刚度kAP等于桥式放大机构的输出刚度[11]。图2为所搭建的压电驱动柔性微纳定位平台的力学模型。图中Vd(t)为控制电压,kamp为压电控制器的放大系数,R为驱动电路的等效电阻,Vpzt(t)是加在压电驱动器上的电压,x(t)为平台位移输出量,kb为桥式放大机构的位移放大比,kpzt为压电刚度,ms为平台等效质量。

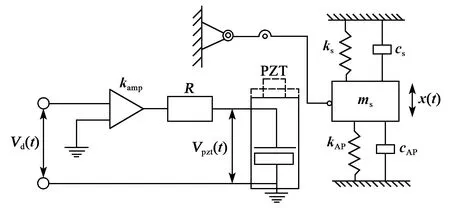
图2 微定位平台机电模型

微定位平台的动力学方程:

AVpzt(t)RCVpzt(t)+Vpzt(t)=kampVd(t)

(1)

(2)

式中:n为压电驱动器的层数;d33为压电常数;C为压电驱动器的等效电容。

根据拉普拉斯变换,将式(1)变成:

(3)

式中ωn和ξ分别为系统无阻尼固有频率和阻尼比。

其中

(4)

(5)

(6)

针对上述二阶系统,柔性机构等效阻尼系数较小,使平台容易产生较严重的低阻尼谐振,从而在平台的通频带内出现自激振荡,严重影响了系统的定位精度、动态品质和控制带宽。

2 谐振频率的在线检测

为有效抑制平台谐振,首先需要对平台谐振频率进行在线检测。在实际的数字控制系统中,采样得到长度为N且非周期的序列x[n],序列x[n]的取样结果决定了傅里叶频谱X[k]的运算结果。序列x[n]和傅里叶频谱X[k]的变换式为

(7)

(8)

(9)

(10)

则离散傅里叶变换形式为

(11)

实现快速傅里叶变换的方法大致分为两类:频域抽取法快速傅里叶变换和时域抽取法快速傅里叶变换。本文采用频域抽取法的FFT,通过蝶形算法完成信号的频域分析[12]。

在压电驱动微定位平台闭环系统中,通常对误差信号进行采样和FFT频谱分析,完成信号时域到频域的转换。将频域值表示为复数R(n)存储在系统缓冲器中,设计的谐振频率提取算法如图3所示。首先求出R(n)点的频率幅值|R(n)|,只有|R(n)|>幅值阈值Hset,若能同时满足|R(n)|>|R(n-1)|,|R(n)|>|R(n+1)|和|R(n)|>Temp,此时将|R(n)|存储在变量Temp中;接着进入下一次循环,直到n=N,结束循环,最后从Temp中获得谐振频率点n。幅值阈值Hset为0.025 dB。通过以上算法求出谐振频率点n,如果采样频率为fs,采样点数为N,则计算出谐振频率为

图3 谐振频率提取算法流程图

f=(n-1)fs/N

(12)

3 自适应陷波滤波器

传统的陷波滤波器不能调节陷波的深度,为了准确地调节陷波滤波器的各种参数,本文在原来的基础上设计了一种改进型陷波滤波器[12]。其传递函数为

(13)

式中:ωn为陷波滤波器中心频率;k1为陷波滤波器深度;k2为陷波滤波器宽度。通过分别调节3个参数可设计满足性能要求的陷波滤波器。

陷波滤波器中心频率ωn的取值是陷波滤波器的设计重点。中心频率是FFT后频谱图里幅值最大对应的频率点,需要根据实际情况进行确定。在前面章节提到的通过谐振频率在线检测获得中心频率,表示为

ωn=f

(14)

陷波滤波器深度k1也是抑制谐振的重要参数。k1的设定数值越小,陷波深度越深,谐振抑制效果越好,但是幅度过大会造成相位滞后,反而会加强振动,所以确定一个合适的k1值是一个重要任务。经过FFT后,深度参数确定为

(15)

式中:Hmax为谐振点处的幅值;Hf为陷波后的信号幅值。

陷波滤波器宽度k2一般是指陷波中心频率两侧,幅度降低到3 dB时两个频点的差。k2值越小,陷波宽度越小,陷波器的抑制效果越好,但也会导致陷波器的群延迟增加。在加入陷波滤波器后,幅值衰减到设置的幅值阈值Hset,幅值阈值水平线与谐振频率两侧的FFT曲线有两个交点,频率点分别为ω1和ω2,陷波滤波器的带宽为

k2=2max{(ωn-ω1),(ω2-ωn)}

(16)

4 轨迹跟踪实验

根据以上结果设计了基于自适应陷波滤波在线谐振抑制的闭环控制方法,如图4所示。由图可见,利用偏差信号进行快速傅里叶变换,在线获得平台谐振特性,调整陷波滤波器参数,实现平台谐振的在线抑制。实验过程中,首先调节PID闭环反馈控制器的比例、积分和微分增益,分别设置为2.5,160和0,在未加入自适应陷波滤波器前,过大的系统增益会使系统出现较严重的谐振现象。随后对系统的误差信号进行采样,采样频率为1 kHz,对1 024个采集到的误差信号进行FFT频谱分析,利用图3所示流程对谐振频率特性进行检测,并对陷波滤波器参数进行在线自适应调整。第1个频谱分析周期的分析结果如图5所示。

图4 在线谐振抑制的结构框图

图5 误差信号的FFT频谱分析结果

为了验证所设计自适应陷波滤波器的谐振抑制效果,对阶跃信号和振幅为0.5 V的不同频率三角波信号进行轨迹跟踪实验,所得实验结果如图6、7所示。

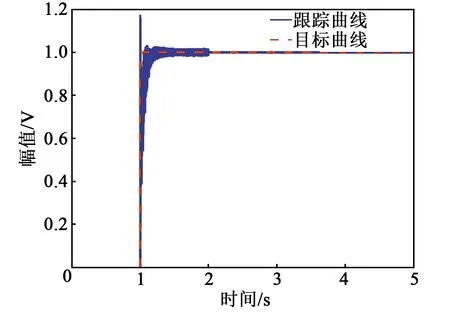
图6 阶跃信号跟踪效果

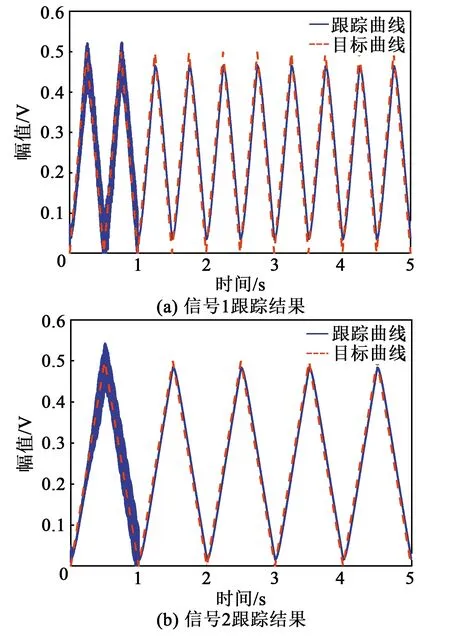
图7 不同频率三角波跟踪效果

由图6、7可知,控制系统对阶跃信号和多轴频率三角波信号进行了轨迹跟踪,由此可见,低阻尼谐振现象得到有效抑制,同时兼顾了稳定性的要求。在此基础上,通过设计高增益反馈控制器可实现压电陶瓷驱动柔性微纳定位平台的高精度轨迹跟踪控制。

5 结束语

本文基于FFT设计出可以实时调整宽度、深度和中心频率的自适应陷波滤波器,有效地抑制了谐振现象,实现了压电驱动柔性微定位平台的精准控制。首先,搭建了压电驱动柔性微纳定位平台系统并进行动力学建模,解释了谐振现象;其次,利用FFT分析系统中的误差信号,设计谐振频率在线提取算法,实现对陷波滤波器参数的在线实时整定;最后,利用所设计的陷波滤波器对阶跃信号和不同频率的三角波信号进行轨迹跟踪实验。实验结果表明,所设计的自适应陷波滤波器能够较好地跟踪不同频率下各类轨迹信号,低阻尼谐振现象得到有效抑制,满足了微定位平台的跟踪性能要求。