基于PINN的变截面压电半导体纤维力学特性研究

吴文锐,房 凯,李 鹏,钱征华,2

(1.南京航空航天大学 航空学院,航空航天结构力学及控制全国重点实验室,江苏 南京 210016;2.南京航空航天大学 航空学院,直升机动力学全国重点实验室,江苏 南京 210016)

0 引言

压电半导体材料兼具压电特性和半导体特性,被用于制造各种电子器件,在智能材料与结构领域具有广阔的应用前景。在压电半导体材料中,机械力可产生极化电荷,与极化相关的电场驱动载流子定向移动,从而实现了机械载荷对载流子传输的控制,这种自供能特性为电子器件的微型化提供了便利。近年来,许多新的压电半导体结构已经被合成,包括纤维、管、带、螺旋和薄膜等[1-2],这些结构以单个或阵列的形式组成了许多新型电子器件,如场效应晶体管、压电传感器[3]、纳米发电机[4-5]等,在工程应用中发挥着重要作用。

已有研究表明,在压电半导体介质上施加非均匀应变可以有效提高压电性能[6],这为高灵敏度压电半导体器件的结构设计提供了新思路。基于此,人们期望通过渐进变化的截面来获取非均匀应变,进而提高自供电器件的压电性能,锥形压电半导体纤维是典型结构之一。此外,受加工工艺及工作环境的影响,器件的形状也会发生变化,如机械加工过程中的缺陷、使用过程中的生物和化学腐蚀等,这些都可导致器件表面凹凸不平[7]。

为了分析变截面压电半导体结构的力学特性,国内外专家学者开展了一系列相关研究。Ren等[8]采用应变梯度法,考虑了应变梯度效应,得到非均匀纳米线轴向延伸下载流子和机电场分布的理论解。Elouafi等[9]基于Mori-Tanaka模型和Eshelby张量,推导了横观各向同性压电材料有效性能的解析和半解析表达式。Yang等[10]基于压电半导体宏观理论对一维模型进行了分析,从理论上证明了压电介质和非压电半导体复合光纤中的PN结与纤维的弯曲变形直接相关。Giuseppe Romano等通过解析和有限元仿真,研究了垂直压缩氧化锌纳米线中自由载流子对压电场的屏蔽效应。类似的相关研究很多,但绝大多数都是针对特定的截面变化模式开展理论分析[10-13],当压电半导体纤维的截面以任意函数形式变化时,其动力学控制方程为变系数偏微分方程,数学上难以求得具有一般形式的理论解。为了解决这一难题,文献[7]提出了幂级数展开法,将压电半导体材料的截面变化函数、位移场和电势场表达为沿纤维长度方向的幂级数形式,但受限于级数的收敛性,该方法并不能求解截面模式任意变化下压电半导体纤维的压电特性。另一方面,现有对压电半导体材料的力学特性研究常是基于线性化假设,对压电半导体本构方程进行了线性化处理,即假设压电半导体材料中载流子的变化远小于初始载流子浓度,这种近似得到的线性解仅适用于外部载荷较小的情况[14-15],当外部载荷逐渐增大时,线性化假设不再适用。

为了精确计算任意截面变化模式下压电半导体纤维的静力学特性,本文创新地提出了基于物理信息的神经网络(PINN)模型,应用深度学习算法求解复杂的变系数偏微分方程。该方法降低了对实验或模型数据的依赖[16],将潜在的物理定律编码为先验信息,可对复杂高阶多维方程进行正向计算,不受几何空间限制,处理边界条件灵活,适用于任意截面形状的压电半导体。此外,该方法既能基于线性化假设进行求解,还能直接求解非线性方程,具有非常好的普适性。本文先以静态拉伸变形下的压电半导体的线性化方程为例,介绍PINN方法的基本原理及实现过程,通过与有限元仿真的对比验证了该方法的正确性;再在此基础上研究了不同的截面变化模式对压电半导体纤维PN结物理特性的影响;最后应用类似的思路求解了压电半导体的非线性方程,充分验证了PINN方法的适用性和通用性。本文方法及结果可为压电半导体器件的结构设计及应用提供重要的理论基础。

1 应用PINN求解压电半导体力学特性的基本原理

1.1 压电半导体材料的基本方程

对于压电半导体材料,其控制方程包括运动平衡方程、静电电荷方程、电荷(电子与空穴)的连续性方程[17-19],即

(1)

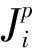
(2)

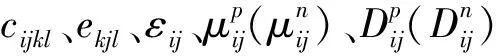
(3)

Ei=-φ,i

(4)

1.2 变截面压电半导体纤维的理论建模

图1为变截面压电半导体纤维受拉示意图。

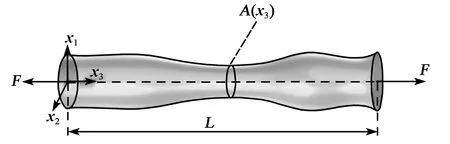
图1 变截面压电半导体纤维受拉示意图

考虑图1中长度为L的变截面压电半导体纤维,其截面面积由函数A(x3)所决定,且在端部受到大小相等、方向相反的拉力F作用下发生变形。本文先从线弹性理论框架下研究变截面压电半导体纤维的拉伸特性,即假设压电半导体材料中电子(空穴)的变化远小于其初始载流子浓度。假设该纳米纤维是电隔离的,无任何电荷或电流,在仅考虑拉伸变形下,结合式(2)-(4),控制式(1)中的运动平衡方程、静电电荷方程可退化[7]为

(5)

(6)

电荷连续性方程可改写为

(7)

(8)

这里考虑了应力松弛条件,对弹性常数、压电常数和介电常数进行了修正,即

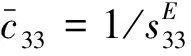
(9)

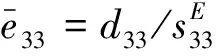
(10)

(11)

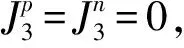
(12)

(13)

式(5)、(6)可统一为

(14)

考虑到纤维两端的应力边界条件σ33=F,故纤维两端的电位移边界条件D3(0)=D3(L)=0可进一步化简为

(15)

(16)

于是,求解图1中变截面压电半导体的拉伸问题可归结为寻找同时满足式(12)-(16)的理论解。由于截面是变化的,式(14)是变系数的微分方程,难以找到适用于截面形式任意变化的通用理论解,一些理论解或数值解多数都是针对某种特定的截面变化模式。为了解决这一难题,本文将基于PINN对该问题进行求解,并研究截面的非均匀变化对压电半导体纤维拉伸变形的影响。这种方法最大的优势在于其具有广泛的适用性,适用于任意截面形状的压电半导体纤维。

1.3 PINN的数值计算流程

神经网络具备强大的拟合能力,可以拟合任何非线性函数,但因其搜索空间庞大,导致寻优难,而为神经网络设置合理的约束是利用其拟合能力的有效手段。利用深度神经网络拟合变截面压电半导体纤维的拉伸问题同样如此。为了解决求解过程中寻优难、训练样本需求大的问题,本文将压电半导体纤维的物理变化规律作为先验知识,利用其约束预测网络的求解空间。本文构建的PINN深度机器学习技术求解变截面压电半导体纤维拉伸问题的基本步骤如下所述。

基于压电半导体的本构方程和控制方程式(12)-(14),可构造损失函数:

(17)

图2 基于压电控制方程的深度学习网络结构

首先,将多个神经元按照多层结构在输入、输出之间连接,构成一个以x3和A(x3)为输入,以φ、Δp、Δn为输出的全连接神经网络(其中φ、Δp、Δn分别表示压电纤维内部的电势、电子浓度扰动、空穴浓度扰动),除最后一层外,其余的各层都是“线性变换+激活函数层”。激活函数给神经元引入了非线性因素,解决了线性模型的非线性缺陷,使得神经网络可以逼近任何非线性函数。在常见的激活函数中,由于双曲正切函数具有输出范围广、梯度不易消失的特点,因此,本文选择双曲正切函数作为激活函数,从而把函数值压缩到[-1,1]区间[21]。

神经元前向传播的过程可表示为

(18)

式中:a为网络层中的单个神经元;上标l为层序号,下标j,i分别表示该层的第j个神经元和前一层的第i个神经元;w和b分别为两个神经元之间对应的权重和偏差;g为激活函数。第L层为输出层,输出的拟合函数为

(19)

本文选取PINN的目的是寻找一组网络层参数,对输入x3和A(x3)进行处理,使输出φ、Δp、Δn逼近微分方程的真实解。

其次,对输出进行自动求偏微分,构成逼近函数,并将深度人工神经网络形成的逼近函数作为试函数[22]。结合压电控制方程式(12)-(14),构成方程的损失函数:

(20)

同时,将边界和初始条件代入人工神经网络函数,结合边界条件式(15)、(16),构成边界损失函数:

(21)

式中wfi和wui分别为方程损失函数和边界损失函数中各部分对应的权重系数。权重系数的选取应尽量使得方程损失、边界损失各项当中的φ,3处于同一数量级,使神经网络对各项损失具有相似的关注程度,以避免某些影响偏微分方程的损失项被忽略。神经网络各层之间的权重和偏置可以通过最小化均方误差损失来进行神经网络深度学习。

最后,定义整体损失函数为Loss=MSEf+MSEu,通过不断迭代优化网络权值,减小损失函数值,直至达到足够合理的机器学习精度。此时,该神经网络逼近的数值即为本文变截面压电半导体纤维拉伸问题的最终解。由算法的具体过程中可见,本文方法不受截面函数A(x3)的影响,适用于截面以任意函数形式变化的压电半导体纤维。

2 基于PINN的变截面PN结物理特性分析

2.1 变截面PN结

为了验证PINN方法在求解变截面压电半导体纤维力学特性的适用性,本文选择半导体领域的基本单元PN结为例进行研究。它由P型和N型两种半导体连接而成,如图3所示。由图可见,当构成PN结的半导体材料具有压电特征时,外部施加的机械载荷可诱导结构内部出现极化电场,进而驱动载流子的定向移动,以实现对半导体器件性能的调控。因此,开展PN结结构的性能分析对半导体器件现代功能的研发和设计都具有重要意义。

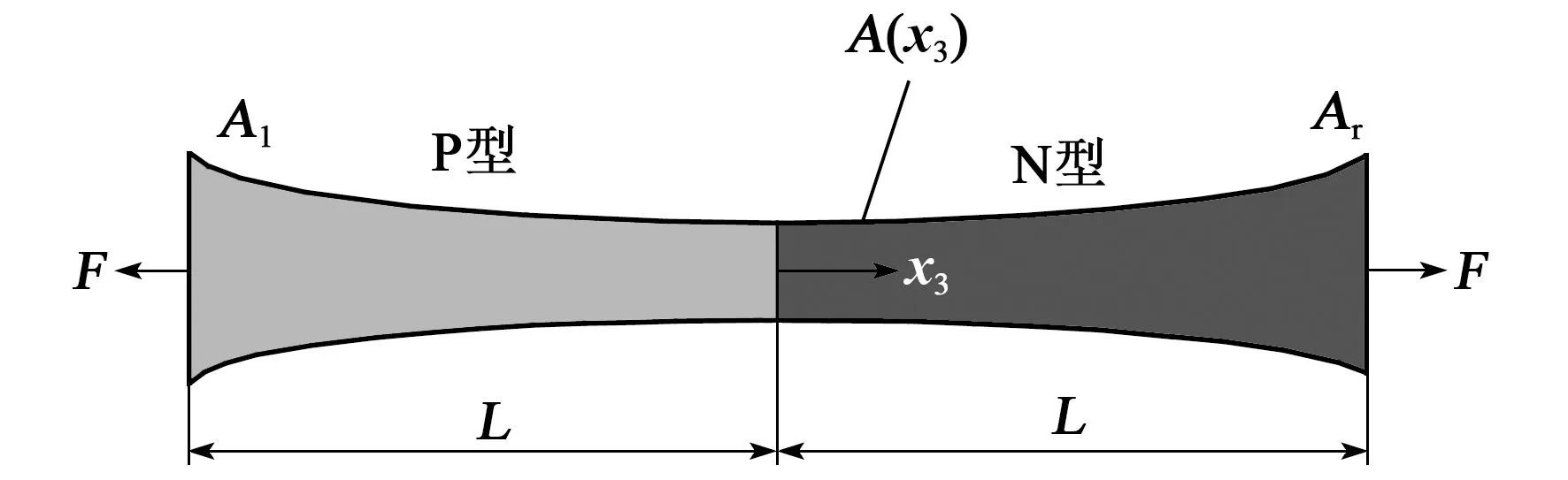
图3 变截面PN结示意图

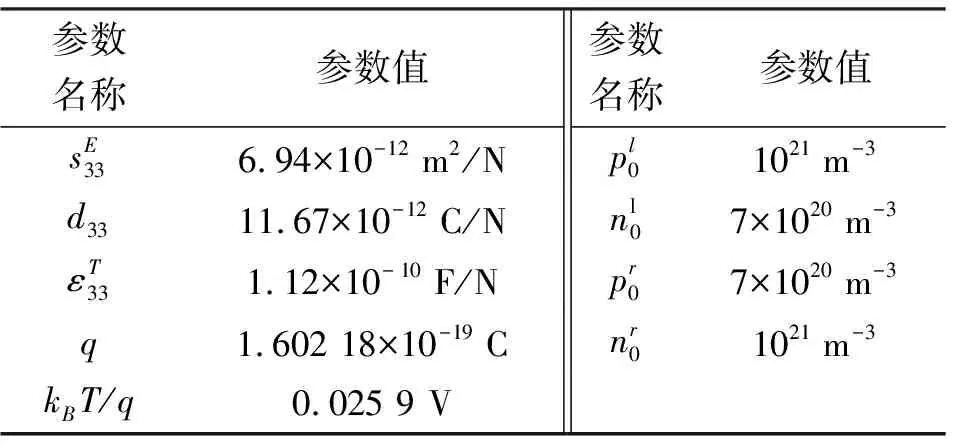
表1 ZnO的材料参数

考虑到x3=0的位置对应PN结的交界面,设置电势的参考零点为φ(0)=0。对于图3所示的PN结,除边界条件要求的D3(-L)=D3(L)=0外,还需满足以下连续性条件:

(22)

此外,PN节处于平衡状态时需满足全局电中性条件[14,17],即

(23)

2.2 正确性验证

本文选取x3=±L处压电半导体纤维的半径为0.09 μm,相应地,A0=0.02 μm2,Al=Ar=0.025 μm2。不同F作用下压电半导体纤维的电势沿x3轴的变化趋势如图4所示。

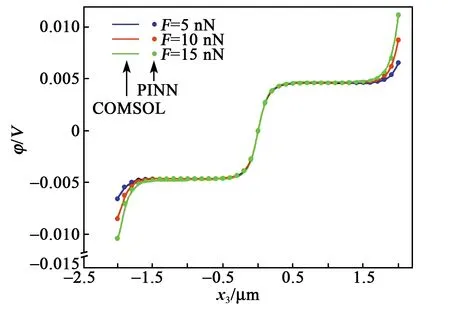
图4 使用PINN法和有限元仿真结果的正确性验证

此外,为了对比,本文还使用有限元软件COMSOL Multiphysics的PDE模块进行仿真分析,得到了不同外力情况下ZnO纤维的电学特性。由图4可见,使用PINN法得到的结果与通过有限元仿真得到的结果高度吻合,这说明了本文方法的正确性。除二次函数外,经核验,通过PINN计算得到的其他截面变化模式下的电学响应均与有限元仿真结果高度吻合。限于篇幅,这里不再一一给出。这充分说明了本文方法的正确性和适用性。同时,电势关于坐标原点沿x3方向反对称分布,这是由压电半导体纤维的对称性所决定。不同外力改变了纤维内应变的大小,而在纤维的势垒区内部,电势完全被自由电荷屏蔽[24],故仅在纤维端部,应变的改变通过压电效应使电势发生了明显的变化。

2.3 颈缩截面的影响

本节仍以横截面积变化函数A(x3)=A0(1+αx32)为例,研究颈缩构型对压电半导体纤维PN结内部力电耦合特性的影响。研究过程中固定外力F=5 nN,分别讨论两种情况:

1) 两端Al和Ar的截面积保持不变,为0.025 μm2,而交界面面积A0可变,其结果如图5(a)所示。

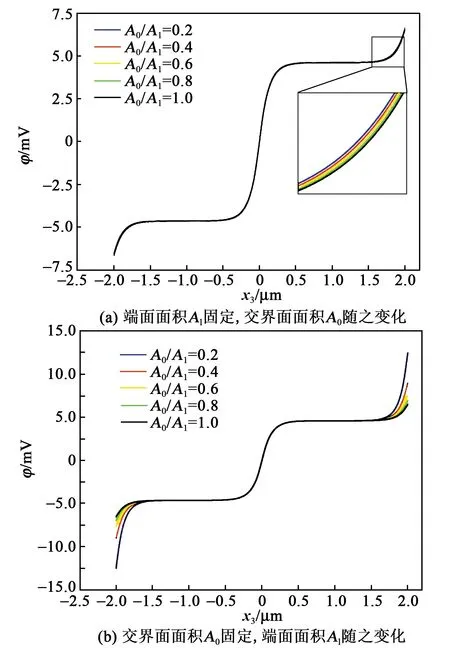
图5 不同端面比A0/Al的颈缩构型纤维中电势φ的分布

2) 交界面A0的截面积保持不变,为0.025 μm2,而两端Al和Ar的面积可变,其结果如图5(b)所示。

相比于A0=Al=Ar=0.025 μm2的均匀压电半导体纤维构型,A0/Al数值发生变化时,工况1)的截面积变化剧烈的部分主要发生在PN结势垒区内部,而工况2)则主要发生在两个端面附近。由图5可见,在一对恒定作用力的作用下,随着A0/Al值的减小,端面电势φ逐渐增大,但两种情况的变化幅度有着明显差别,图5(b)中的端部电势变化更显著。这是因为端部的应变变化对附近电荷分布有影响,而在PN结的势垒区内部的场被自由载流子完全屏蔽,中部应变改变并不会对附近电荷分布有影响,因此,势垒区内部的截面积变化几乎不会改变PN结的压电性能。

2.4 锥形端面构型

为了进一步说明PINN方法在求解任意截面形状的压电半导体纤维结构的适用性和通用性,本节选取左端为锥形端面的压电半导体纤维进行分析,其构型如图6所示。

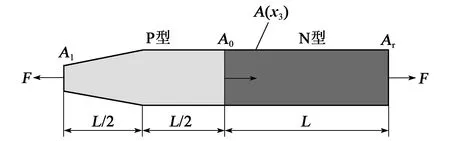
图6 锥形端面构型的变截面PN结示意图

假设外力F=5 nN,A0=Ar=0.025 μm2,横截面积A(x3)可用如下的分段函数表示:

A(x3)=

(24)

式中左端的切屑部分用线性函数来表征。

图7是图6所示的压电半导体纤维中的电势分布。由图可见,端面截面积的改变对电势的改变影响较显著,这是因为随着左端面截面积的减小,该区域的强度降低,在相同的拉力下产生了较大的应变,进而通过压电效应产生的电场较大。这种改变仅发生在势垒区外的端面位置附近,而结区附近的势垒构型基本无变化。

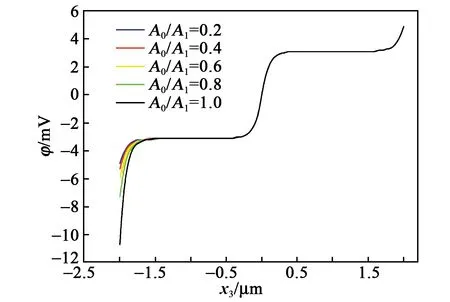
图7 不同端面比A0/Al所对应的纤维中电势φ的分布

综合图5、7可知,对于具有相同初始载流子浓度的非均匀压电纳米纤维PN结,其势垒区内部具有大致相同的电势及电场特性,而端面截面积的改变对电场特性的影响显著,变截面压电半导体纤维在端部位置表现出很强的结构依赖行为,工程应用中可以利用这类特性来提高压电纳米纤维器件的灵敏度[8]。

2.5 压电半导体纤维非线性方程求解

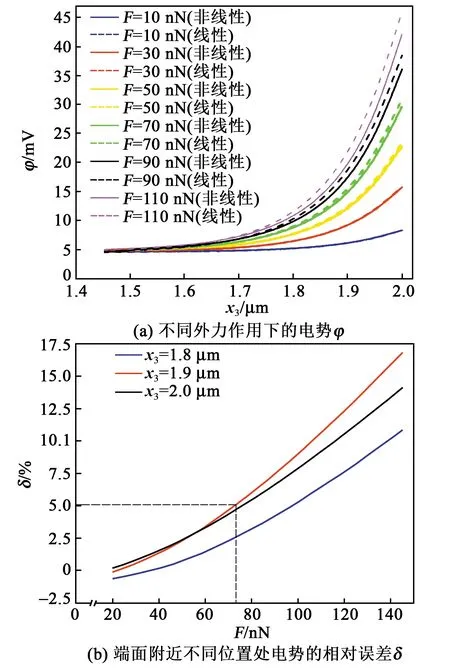
图8 线性化法与非线性法计算结果对比

由图8可见,当外力F较小时,线性和非线性两者之间的误差较小,这间接验证了线弹性压电半导体理论的正确性。随着两端拉力F的增大,纤维端面及交界面的载流子浓度扰动提高,电势随之增大,这是因为线性化的控制方程略去了含Δn和Δp的增量项,因而产生了一定的误差。由于压电纤维端面附近的载流子浓度扰动最大,故误差最大的位置也位于该区域内。此外,通过线性化法计算得到了比真实工况更高的电势值,且此误差随着纤维两端机械载荷的增大而被逐渐放大。为了进一步量化分析,本文定义相对误差δ为

(25)

端面附近不同位置处的相对误差随外力F的变化趋势如图8(b)所示,图中x3表示端面附近的坐标。由图可见,随着外力的增大,线性结果所产生的误差会逐渐增大,这是因为线性化法略去了包含载流子浓度扰动的增量项,而该增量项在载荷较大的情况下影响更明显。同时在实际应用中,在最大误差允许的范围内可得到线弹性压电半导体理论的适用区间。例如,如果最大相对误差设为5%,则外界拉力的临界值F临界值=70 nN。当F>70 nN时,线弹性压电半导体理论的计算结果会导致相对较大的误差,此时必须考虑压电半导体方程的非线性项;而当F≤70 nN时,线弹性压电半导体理论的计算结果相对误差较小,可以接受。

3 结束语

本文构建了基于物理信息的深度学习神经网络模型(PINN),并给出了计算模型及神经网络模型的构建过程。在此基础上,以变截面压电纳米纤维PN结为例进行了压电性能预测,通过与COMSOL仿真结果进行对比,验证了模型的正确性和有效性,为复杂压电半导体器件的结构设计提供了理论基础。该方法以计算机深度学习的方法代替了复杂的非线性方程求解,可用于求解压电半导体问题的线性解和非线性解,对任意截面形状的压电纳米纤维模型均适用,具有良好的普遍性。本文主要研究了压电半导体纤维的静态拉伸特性,可以预见,PINN方法对于压电半导体材料的弯曲、扭转及动态问题的求解依然适用。