考虑螺栓断裂的固体导弹水平跌落安全性分析

吴振宇，张韬,2*

考虑螺栓断裂的固体导弹水平跌落安全性分析

吴振宇1，张韬1,2*

（1.北京理工大学 机电学院，北京 100081；2.大连理工大学 工业装备结构分析优化与CAE软件全国重点实验室，辽宁 大连 116024）

通过数值仿真分析水平跌落条件下的固体导弹安全性。基于LS-DYNA进行全弹水平跌落仿真计算，通过位移和加速度的实验测量值进行模型校核。重点分析螺栓断裂对结果的影响，对比螺栓在不同建模方法、不同断裂数量下的仿真结果。基于经过校核的全弹模型，计算含能材料的应力场。不同建模方法中，螺栓连接法的加速度峰值计算精度最高；不同工况之中，三部段工况下的螺栓断裂数量与实际一致，且加速度峰值计算精度最高。根据精度最高的仿真模型计算出的全弹应力响应，战斗部与发动机装药内部最大Von Mises应力均小于反应阈值。螺栓连接的建模方法和断裂数量对于全弹位移、加速度的计算精度具有显著影响。采用螺栓连接法建模的三部段工况仿真模型最为可靠。基于可靠模型的含能材料应力场计算结果表明，全弹6 m水平跌落不会直接引起战斗部、发动机装药反应。

有限元分析；水平跌落；螺栓连接；螺栓断裂；含能材料；弹药安全性

弹药的安全性对于避免弹药意外损耗，减少部队非战斗损失具有重要意义。世界各国对不敏感弹药投入了大量研究，并制定了弹药安全性评估标准，其中机械刺激下的安全性是必须考虑的标准之一。对固体导弹而言，吊装跌落是具有代表性的安全事故，因此需对跌落条件下的固体导弹安全性进行分析。

国外的安全性评价标准将水平跌落试验作为安全评估手段之一，如美国国防部提出的MIL-STD- 2105D 《常规弹药危险性评估试验》、北约提出的STANAG 4439《不敏感弹药的介绍、评估和试验政策（MURAT）》（第三版）以及AOP-39《不敏感弹药的研制、评估和试验指南》（第三版）等[1]。STANGAG单项实验程序对应的基本安全性试验中就包含了12 m跌落试验，见表1。采用12 m跌落作为机械刺激的代表类型有2个方面的原因：导弹跌落是最典型的机械类事故之一；该条件下的撞击刺激强度足以覆盖大多数使用场景下机械刺激的强度。

表1 STANAG不敏感弹药安全性试验程序

我国也开展过弹头、发动机或全弹的跌落安全性试验与仿真研究。早在1986年，〇一四中心就已进行空空导弹发动机的跌落试验[2]。江明等[3]总结了国外弹药安全性实验方法，提出了包括跌落试验在内的我国导弹战斗部安全性考核试验方法和评估准则，并试验验证了某型战斗部的跌落安全性。张学伦[4]综合分析对比了国内外战斗部跌落安全性相关标准的优缺点，提出了修订现行国内战斗部跌落安全性试验标准应关注的内容。谢涛等[5]利用LS-DYNA模拟了空空导弹战斗部的12 m垂直跌落过程，结果表明，药柱内部最大Von Mises应力为34.1 MPa，小于炸药的临界起爆压力，炸药处于安全状态。杨明等[6]利用LS-DYNA软件模拟了固体发动机的37.5 m垂直跌落过程，结果表明，发动机尾部的壳体和装药的应力、应变较大，其中装药应力最大值为0.69 GPa，但是推进剂的温升较小，仅为5.45 K，不会发生点火反应。崔浩等[7]基于圆筒试验标定的JWL状态方程参数，利用AUTODYN软件进行了固体发动机的跌落模拟试验，测定推进剂临界起爆压力为2.675 GPa，发动机径向跌落靶板临界起爆速度范围为150～200 m/s。张斌等[8]将数值仿真与应力波分析相结合，研究了跌落姿态、高度以及装药构型对于构型弹体的冲击响应特征的影响，结果表明，装药变形主要由于内部应力波造成，药柱构型对药柱变形区域分布具有重要影响。陈马旭等[9]通过ABAQUS模拟了装有泡沫的导弹包装箱跌落地面的过程，结果表明，聚氨酯泡沫对于导弹具有保护作用，导弹应力大小在安全范围内。

总体而言，目前针对导弹跌落安全性的研究存在2方面局限性：一方面，大多数研究选择战斗部或发动机作为研究对象，仅获得单一部件的仿真或试验结果，但某一部件在单一部件跌落试验中的动力学响应无法代表全弹跌落试验中该部件的动力学响应。另一方面，少数以全弹为对象的仿真研究又未能考虑舱段间螺栓连接结构的失效，以及螺栓失效之后导弹解体为数个部段的现象。然而，全弹整体撞击地面与先分解为数个部段再撞击地面截然不同。对于发生了结构解体的全弹跌落试验，不考虑螺栓断裂的仿真将无法准确计算全弹动力学响应，难以有效指导跌落工况中的安全性评价。

本文针对固体导弹在水平跌落条件下的安全性问题，进行了考虑螺栓断裂的全弹动力学仿真研究。通过大量仿真试验，发现螺栓连接件对于仿真结果影响较大。因此，建立了包含部段间螺栓连接结构的全弹简化模型，研究了不同螺栓断裂数量以及不同螺栓连接建模方法对全弹仿真结果的影响，通过位移与加速度的实测值进行了模型校核。计算了战斗部与发动机装药的内部应力，根据含能材料反应阈值，对某固体导弹的跌落安全性进行了评价。

1 理论基础

1.1 基于LS-DYNA的显式动力学分析

对于涉及物体运动、变形的非线性动力学问题，LS-DYNA采用Lagrange形式的描述方法，将物体离散化为物质网格单元，进而使用显式动力学方法求解各离散单元的数值解[10]。以显式动力学的中心差分法为例，对于有限元法，单元节点在时刻满足以下运动方程[11]：

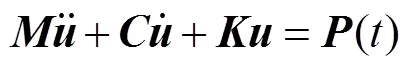
已知0,1,…,t时间步的解，可采用显式中心差分法求t+1时间步的解。根据泰勒展开可知，位移、速度、加速度之间近似满足：

最终t+1时刻的速度和位移可由式（3）、（4）求得：

1.2 跌落撞击问题描述

对固体导弹跌落撞击问题的描述可通过2方面进行：固体导弹的静态结构；撞击过程中导弹结构的动态变化。

某型固体导弹由多节舱段组成，舱段之间采用螺栓法兰连接。由于该导弹需要实现级间分离，所以在分离面处采用了含火工分离的螺栓法兰结构。这样的火工分离面在全弹中有2处，将全弹分为3级：第I级以弹头为主要部件，整体呈圆锥形；第II级以末端修正舱为主要部件，整体呈圆台形；第III级以发动机为主要部件，整体呈圆柱形，如图1所示。

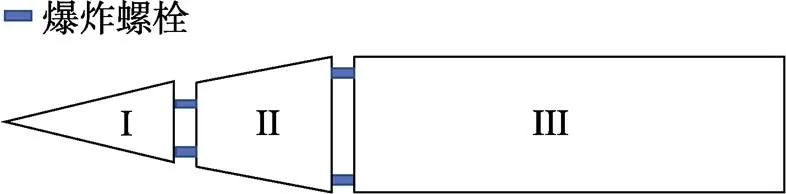
图1 全弹结构分级示意图

在全弹跌落试验中，导弹以水平姿态静止悬吊于6 m高度，释放后经过自由落体加速阶段跌落至地面。由于导弹各级的圆锥角不同，第III级将最先接触地面。此时第I级与第II级尚未触地，所以将保持向下运动的趋势。在不考虑任何结构断裂的假想情况下，地面施加给第III级的冲击力将以第III级前端为轴形成扭矩，驱动全弹向前翻滚，如图2所示。同时，全弹先经历挤压变形阶段，而后进行高度重新上升的回弹阶段。根据6 m跌落试验的结果，级间分离面上的部分螺栓实际上会发生断裂。在实际情况下，导弹将因螺栓断裂而变为3级牵连体，导致各级段按照III—II—I的顺序逐次撞击地面，如图3所示。该过程可分为4个阶段：

1）第III级触地后挤压变形，而第I级与第II级尚未触地，所以保持向下运动的趋势。数十毫秒后，II-III级间上侧的螺栓因无法承受两侧舱段施加的拉伸、剪切力而断裂。

2）I-II级以II级尾端为轴心，作为整体逆时针转动，而第III级则继续挤压变形-回弹过程。此过程持续数十毫秒。

3）第II级碰撞地面后，开始挤压变形，而第I级仍未触地，所以保持逆时针转动的趋势。数毫秒后，I-II级间上侧的螺栓因无法承受两侧舱段施加的拉伸、剪切力而断裂。

4）第I级以I级尾端为轴心逆时针转动，与此同时，III级、II级依次进入高度重新上升的回弹阶段。最终全弹以III-II-I牵连体的形式回弹。

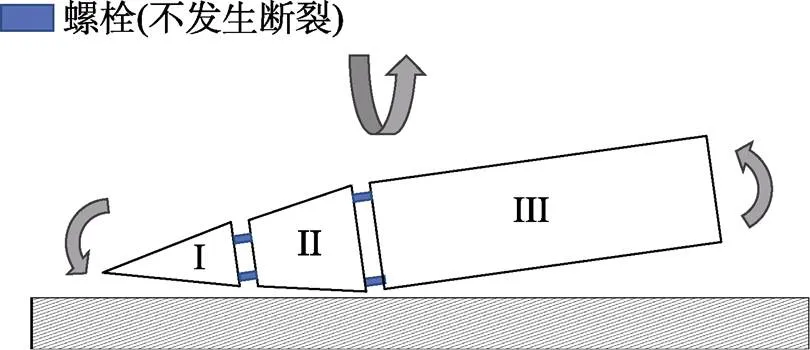
图2 假想跌落撞击情景

图3 实际跌落撞击情景

1.3 装药安全性分析判据

将炸药、推进剂发生反应的应力阈值作为战斗部、发动机装药安全性分析的判据[5]，而炸药与推进剂发生反应的应力阈值可以在撞击感度试验中测量。撞击感度落锤试验中，不同加载条件下B炸药与HTPB推进剂药片的反应阈值见表2[13-19]。

由表2可见，不同加载条件下，药片反应的应力阈值有所不同。为了判断全弹跌落试验中战斗部、发动机装药的安全性，可以从不同的应力阈值中选取最小值，以近似表征装药不发生反应的边界值。在所有试验结果中，选取了药片发生反应时应力阈值之中的最小值[13,18]，以此作为炸药、推进剂不发生反应的安全阈值。若仿真结果中战斗部、发动机装药的应力值超过该安全阈值，则战斗部、发动机装药有可能在6 m水平跌落条件下发生反应，反之则不会发生反应。

表2 落锤试验中B炸药与HTPB推进剂的应力阈值

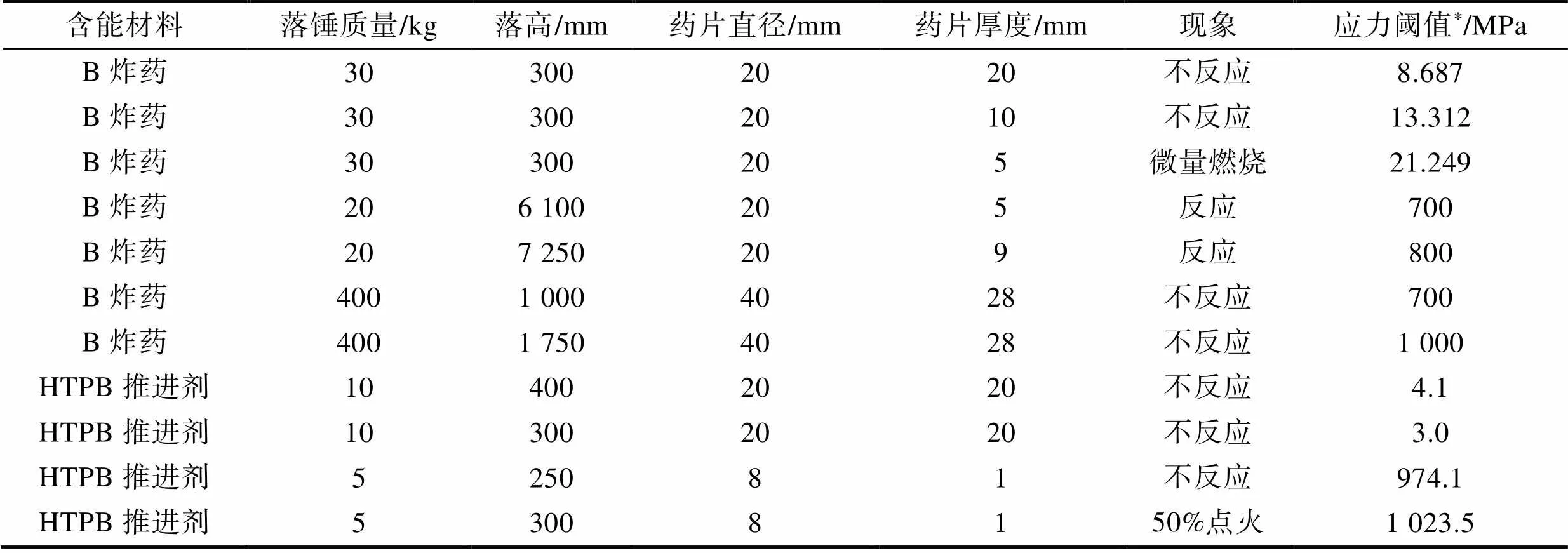
Tab.2 Stress threshold of reaction of Comp.B dynamite and HTPB propellants

*注：当药片不反应时，仅记录应力时程曲线中的应力峰值。

2 仿真模型

2.1 几何模型

在建立有限元模型时，将全弹结构简化为I、II、III等3级。其中第I级壳体内填充有战斗部装药、第III级壳体内填充有发动机装药，如图4所示。

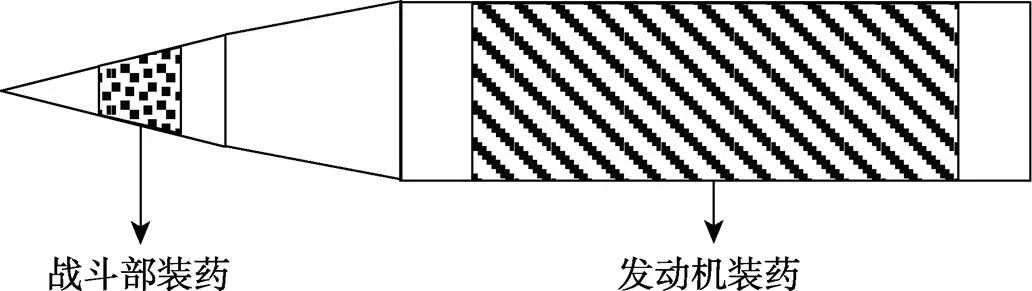
图4 全弹简化结构

2.2 材料模型

2.2.1 Johnson-Cook本构模型

本文进行的全弹水平跌落仿真中包含了导弹壳体、炸药等材料的碰撞计算，这些材料选用了Johnson-Cook材料本构模型。Johnson-Cook模型[20-22]是一种基于实验数据拟合的应变率相关的本构模型，考虑了材料的塑性硬化、应变率效应和热软化效应，各项模型参数物理意义清晰，易于实验测定，常用于求解金属材料高应变率下的非线性大变形问题与冲击问题。Johnson-Cook本构模型形式见式（5）。

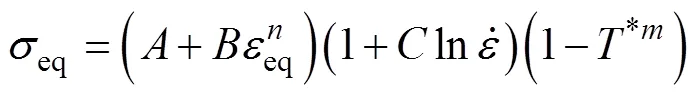
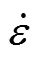
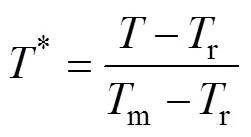
式中：为材料当前温度；r为参考室温；m为材料熔点。

2.2.2 Gruneisen状态方程

在LS-DYNA中使用Johnson-Cook本构方程定义材料模型时，一般要结合Gruneisen状态方程才能实现计算。Gruneisen状态方程是高压条件下一种常用的内能形式的固体状态方程，给出了压力、比容与其他热力学参量间的关系。在LS-DYNA软件中，该材料模型表示如下[24]。

对于受压材料，压力(,)满足：

对于受拉材料，压力(,)满足：

2.2.3 Prony级数形式的广义Maxwell黏弹性模型

HTPB推进剂可以近似视为一种黏弹性材料。人们通常使用弹簧表示材料的弹性行为、黏壶表示材料的黏性行为，而Maxwell模型由1个弹簧和1个黏壶串联组成，可用于表示材料的黏弹性行为。在应力的作用下，弹簧和黏壶的应变分别为1和2，则产生的总应变为两者应变之和，即=1+2。可得：

广义Maxwell黏弹性体由个Maxwell弹性体并联而成，其偏应变率与每个Maxwell黏弹性体的偏应变率相同，偏应力为所有Maxwell弹性体偏应力之和：

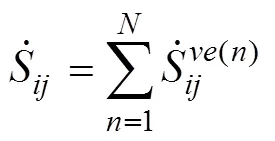
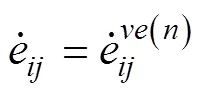
同时，广义Maxwell黏弹性体剪切模量和松弛时间满足：

式中：为黏弹性体数目，亦即广义黏弹性体模型的阶数；代表了第个体元。

广义Maxwell本构模型可以表示为Prony级数形式[24]，对于剪切模量()与体积模量()，有：

2.2.4 材料参数

导弹壳体材料为某合金，密度、弹性模量和泊松比分别取2 780 kg/m3、72.4 GPa和0.33，采用双线性随动硬化本构模型。战斗部装药为B炸药，密度、弹性模量和泊松比分别取1 680 kg/m3、4.33 GPa和0.38，采用Johnson-cook本构模型与Gruneisen状态方程，参数见表3～5[24]。HTPB推进剂泊松比=0.49，密度7 800 kg/m3，采用PRONY级数形式的广义Maxwell黏弹性本构模型，参数见表3、表6[26]。地面为覆盖钢板的混凝土基座，其中钢板材料的密度、弹性模量和泊松比分别取7 800 kg/m3、210 GPa和0.3。混凝土为C40，其密度、弹性模量和泊松比分别取2 500 kg/m3、32.5 GPa和0.2[27]。

表3 各部件的材料模型参数

Tab.3 Material model parameters of components

*注：HTPB推进剂材料参数表示黏弹性材料的初始模量0。

表4 Johnson-Cook模型参数

Tab.4 Johnson-Cook model parameters

表5 Gruneisen模型参数

Tab.5 Gruneisen model parameters

表6 HTPB推进剂Prony级数模型参数

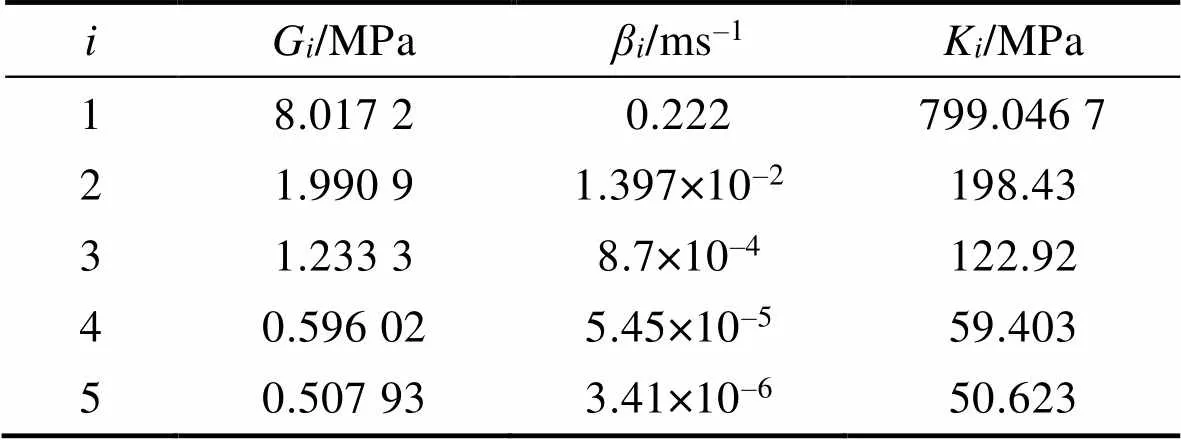
Tab.6 Prony series model parameters of HTPB propellant

2.3 材料失效模型

考虑到螺栓断裂失效的可能性，须对连接结构相关材料进行失效设置。对于钢制螺栓所使用的Johnson-Cook材料模型，可通过在*MAT_JOHNSON_ COOK关键字卡片中设置SPALL参数，选取失效准则。为了表示拉伸载荷下的材料破坏，LS-DYNA提供了3种模型[23]。本文将参数SPALL值设置为2，选用最大主应力层裂模型，并将级间螺栓的失效最大主应力设置为p=500 MPa。如果最大主应力max超过极限值p，该模型将判定层裂发生。一旦该模型检测到固体中的层裂，则将偏应力、静水张力重置为0，同时在剥落材料中将拉伸应力重置为0。

2.4 初始条件与边界条件

全弹水平跌落仿真的初始条件包括全弹的高度、初速度。通过刚体动力学计算可知，即将接触地面时,全弹速度为10.48 m/s，方向竖直向下。因此，将数值仿真的初始条件设置为：全弹模型距离地面50 mm，初速度竖直向下，大小为10.48 mm/ms。

全弹水平跌落仿真的边界条件包括2方面：导弹的载荷、接触与约束设置；地面的接触、约束设置。导弹撞击地面后，全弹所受载荷包括地面冲击力和重力。在全弹与地面之间设置Automatic_Surface_to_ Surface接触。通过*LOAD_GRAVITY_PART_SET关键字设置重力载荷。全弹在各方向的自由度不受约束。

作为撞击对象的地面设置为表面覆盖钢板的混凝土基座。钢板厚度为60 mm，混凝土厚度设置为200 mm。在钢板与混凝土之间设置Automatic_ Surface_to_Surface接触。混凝土底部网格单元自由度受到完全约束，代表不因实验而发生位置变化的参考地面。

2.5 导弹级间螺栓连接设置

经过大量仿真试验，发现不同的螺栓简化模型、不同的螺栓断裂数量对仿真结果具有显著影响。为了对比研究螺栓简化模型的影响，提出了4种简化建模方法。为了研究螺栓断裂数量的影响，提出了3种螺栓连接工况，不同工况下的螺栓断裂数量各不相同。

2.5.1 螺栓简化建模

导弹的级间通过螺栓法兰结构连接，如图5所示。为避免全弹不同部件之间网格尺寸差异过大，需对螺栓结构进行简化建模。

图5 螺栓法兰连接结构建模

螺杆直径为24 mm，长度为100 mm。螺母直径约50 mm，高度约25 mm。将螺杆与螺母的几何形状简化为六棱柱，划分为solid六面体单元，单元尺寸为5 mm。在螺栓与法兰之间、螺母与法兰之间设置Automatic_Surface_to_Surface自动接触。全弹跌落实验中，螺栓头部与螺杆部分之间的连接处发生断裂失效，而螺栓与螺母之间并未发现螺纹破坏现象。根据Chen等[28]对螺栓连接模型的研究，断裂发生在非螺纹段时，使用“绑定”接触替代螺纹连接的简化模型与精细模型之间的误差极小。因此，本文将螺杆与螺母之间的螺纹连接简化为共节点连接。根据田彤辉[29]、王青文[30]对于瞬态冲击下螺栓法兰结构失效的研究，螺栓连接结构预紧力水平对于连接结构的承载能力、失效方式影响可以忽略。因此，本文不对螺栓法兰结构施加预紧力。

出于简便考虑，本文将上述模型简化建模方法称为螺栓连接法。为了研究螺栓简化模型对于仿真结果的影响，除螺栓连接法外，还设计了3种螺栓连接的简化模型作为对照：壳体连接法、简支梁连接法和梁间连接法。简化模型如图6所示，这4种简化模型具体设置的区别见表7。

2.5.2 螺栓连接工况

根据6 m跌落试验的结果，导弹级间分离面上的部分螺栓会发生断裂。本文考虑2处级间分离面上可能出现的螺栓断裂，针对这些螺栓进行断裂失效设置。在考虑2个级间分离面上的螺栓断裂时，全弹可以分为三部段撞击地面，本文将这种螺栓连接工况称为三部段工况。三部段工况下的全弹跌落仿真应当能够获得较为接近实际情况的结果。此外，为了研究螺栓断裂数量对于仿真结果的影响，本文还设置了单部段、两部段工况作为对照组。3种工况下考虑断裂的螺栓的数量与位置如图7所示。3种连接工况下螺栓的断裂失效设置见表8。

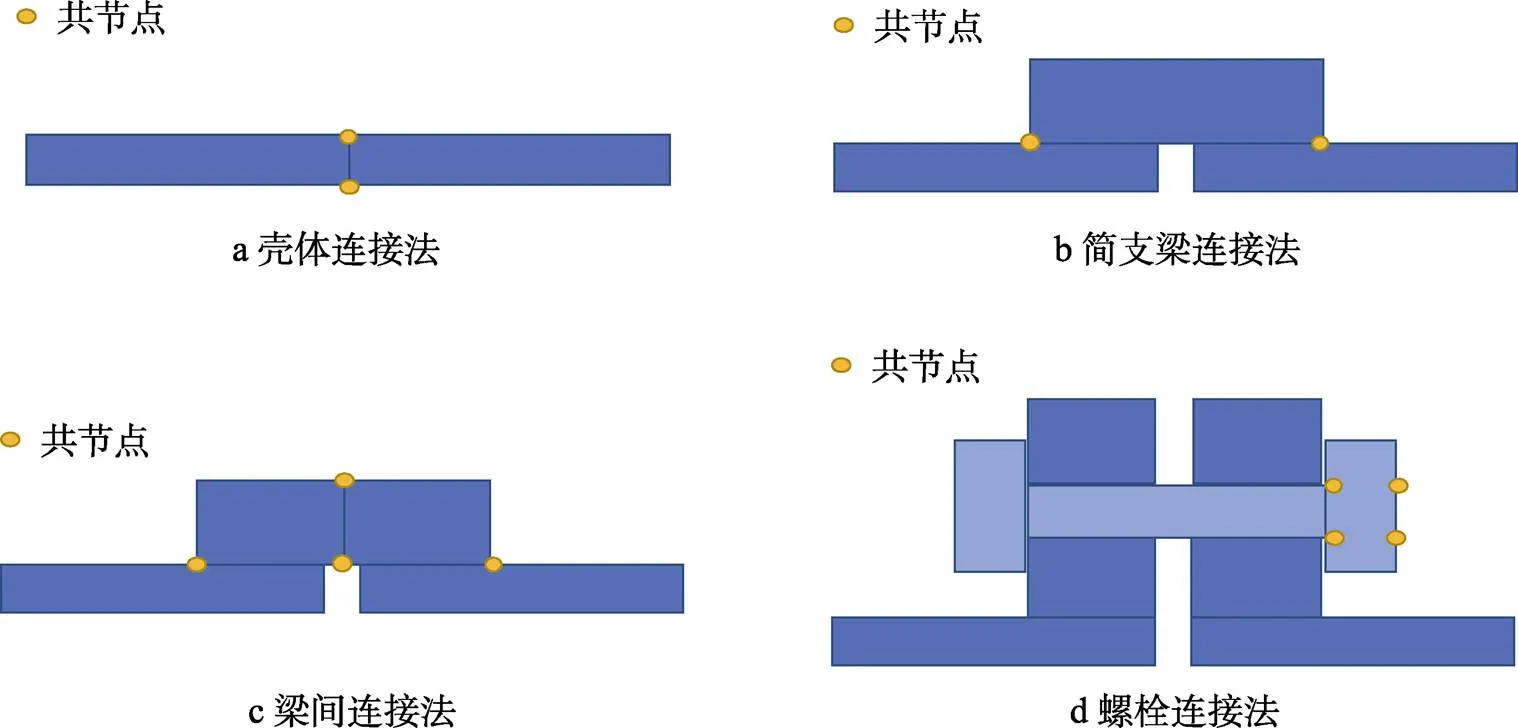
图6 螺栓连接建模方法

表7 螺栓连接建模方法设置对比

Tab.7 Comparison of settings for bolt joint modeling schemes

注：“×”表示该设置不存在；“(+)”表示设置材料失效，“(–)”表示不设置材料失效。

图7 考虑断裂螺栓的工况

表8 3种工况下的螺栓断裂失效设置

Tab.8 Bolt failure settings under three conditions

注：“+”表示设置螺栓断裂失效，“–”表示不设置。

3 仿真结果

基于LS-DYNA进行了结构动力学有限元分析，模拟全弹水平跌落撞击过程。仿真结果分为模型校核与安全性分析2部分说明。通过位移和加速度的实验测量值进行了模型校核，重点研究了螺栓连接对结果的影响，对比了螺栓的不同简化模型、不同断裂数量的仿真结果。基于经过校核的全弹模型，计算了全弹水平跌落的应力响应。根据含能材料内部的应力峰值与1.3节的反应阈值的对比结果，对某固体导弹的跌落安全性进行了评价。

3.1 模型校核

3.1.1 对比位移响应

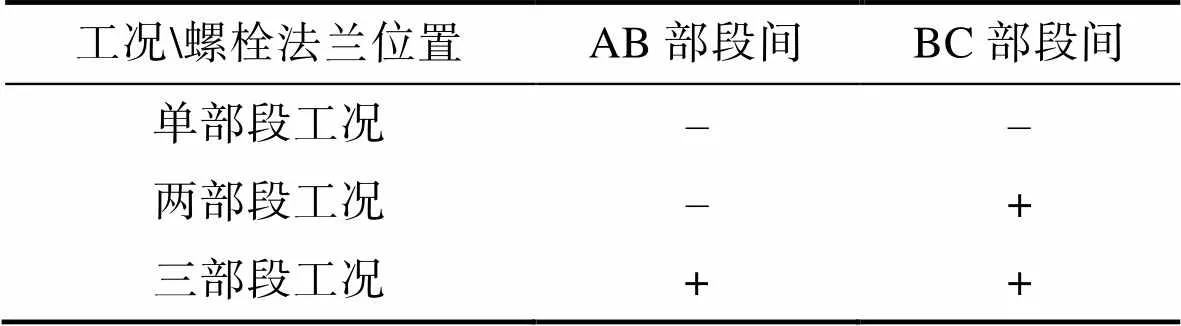
以撞击后的回弹姿态作为位移响应指标，对比撞击200 ms后3种工况的回弹姿态，如图8所示。可见，3种工况下回弹姿态差异显著，单部段工况下，部段倾角大约10°；两部段工况下，I-II部段倾斜角大约20°，III部段倾斜角大约－5°；三部段工况下，I、II、III段倾斜角逐渐减小，依次约为30°、5°、0°。

分别从跌落试验高速摄影图像、3种工况的仿真结果中提取部段中轴线的近似位置，绘制误差折线，如图9所示。计算得出单部段工况、两部段工况、三部段工况的高度误差平均值分别为：95.0、–27.5、－17.5 mm（负号代表高度结果低于实测高度）。可见，三部段工况回弹高度的误差平均值最小。

图8 全弹水平跌落撞击后200ms回弹姿态对比

撞击200 ms后，3种工况下的螺栓断裂情况见表9。对比实际的螺栓断裂情况可知，三部段工况的仿真结果与实际情形一致。综上所述，通过对比位移响应可知，三部段工况模型误差最小，通过模型校核。

表9 全弹水平跌落撞击后200 ms的螺栓断裂情况

注：“—”代表该工况下不考虑此处螺栓的断裂失效。

3.1.2 对比加速度响应

对比3种工况下的仿真结果与跌落试验中的加速度计实测值，以进行模型校核。在全弹不同位置选取5个具有代表性的测点，其中测点1、2、3位于弹头段，测点4位于中间舱段，测点5位于固体发动机段，如图10所示。提取仿真结果中这5个测点的加速度最大值，计算仿真结果与实测值间的误差。

图10 关键加速度测点分布

1）螺栓简化模型的影响。分别使用壳体连接法、简支梁连接法、梁间连接法、螺栓连接法进行全弹跌落仿真，4种方法的测点加速度最大值与跌落试验实测值对比如图11所示，不同方法在各测点的加速度最大值差异较大。其中，考虑了螺栓材料失效的梁间连接法与螺栓连接法计算出的最大值分布曲线与实测值较为接近。表10计算了加速度最大值的相对误差，将4种方法的误差值进行对比，并在绘制了各测点处的相对误差折线，如图12所示。结果表明，壳体连接法、简支梁连接法、梁间连接法不能正确反映实际情况下螺栓连接结构的受力情况，加速度的误差较大，而螺栓连接法的各测点相对误差平均值仅为15.78%，具有最佳的模拟精度。除了此处展示的4种基于SOLID单元的简化模型以外，本文还尝试过基于SHELL单元-SOLID单元共节点连接的简化模型。在该模型的数值结果中，在撞击尚未发生的初始时刻端框部位出现了异常的应力集中，因此该模型同样不能正确反映实际情况下螺栓连接结构的受力情况。综合以上结果可知，螺栓结构的简化建模方法对于模拟精度具有重要影响。其中螺栓连接法的模拟精度最高。

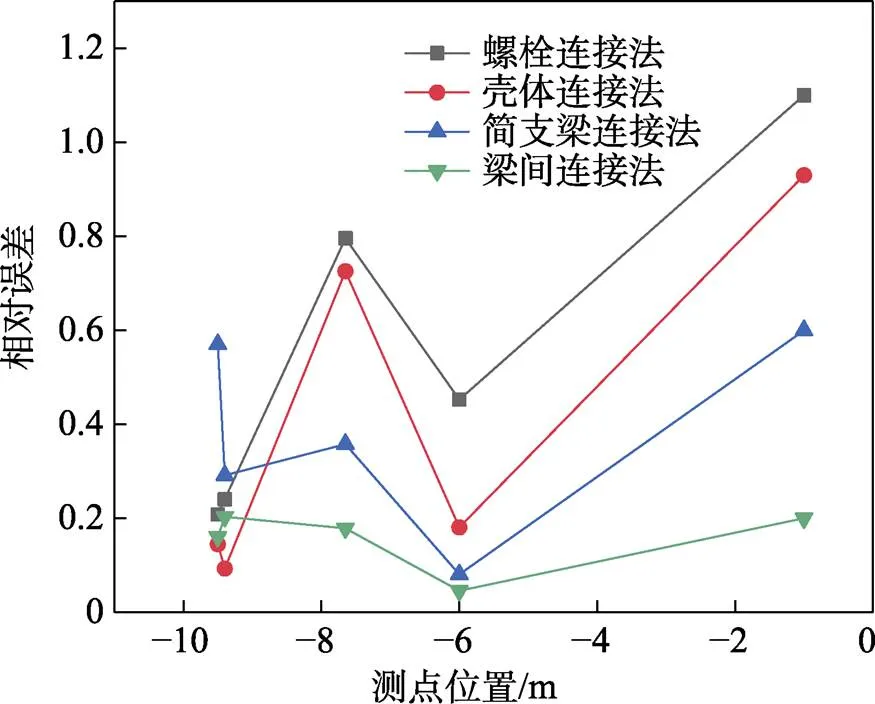
图11 4种建模方法中关键测点处加速度最大值

表10 4种建模方法中关键测点处的相对误差

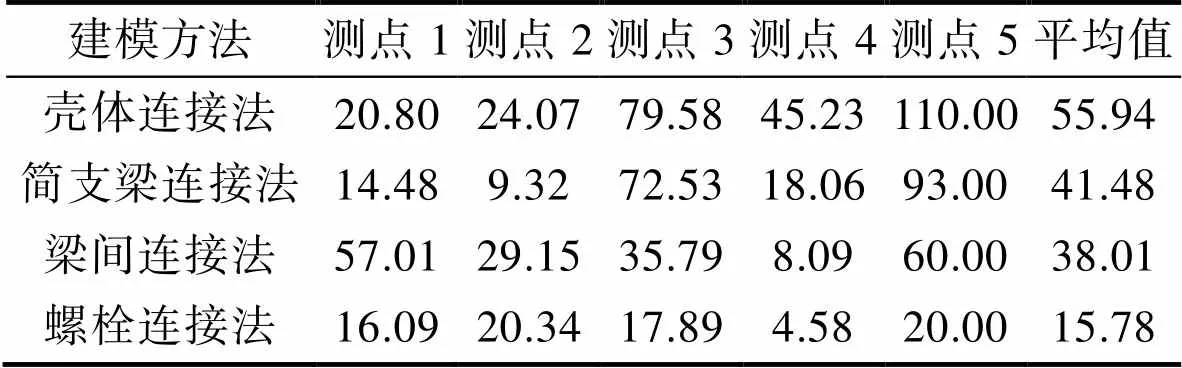
Tab.10 Relative error on key measuring points among four modeling schemes %

图12 4种建模方法中关键测点处加速度相对误差

2）螺栓断裂数量的影响。采用螺栓连接法建立螺栓简化模型，进行3种连接工况下的全弹跌落仿真。3种工况仿真的测点加速度最大值与跌落试验实测值对比如图13所示，不同工况在各测点的加速度最大值差异较大。其中，三部段工况下计算出的最大值分布曲线与实测值较为接近。加速度最大值的相对误差见表11。对比3种工况的误差值，绘制了各测点处的相对误差折线，如图14所示。结果表明，单部段工况的相对误差平均值最大，达到了46.92%。相比之下，两部段工况在测点4、5处的相对误差则有显著减小，分别从27.22%降低到9.97%，从91.44%降低到44.00%。这是因为考虑了II-III级间分离面的螺栓断裂，使得第III级的动力学响应更接近真实工况。相比两部段工况，三部段工况在测点3处的相对误差显著减小，从72.53%降低到17.89%。这是因为考虑了I-II级间分离面的螺栓断裂，使得第I级的动力学响应更接近真实工况。三部段工况下的各测点相对误差平均值仅为15.78%，具有最佳的模拟精度。通过对比不同螺栓简化模型、不同螺栓断裂数量的加速度响应可知，基于螺栓连接法的三部段工况模型误差最小，是通过模型校核的全弹模型。

图13 3种工况下关键测点处加速度最大值

表11 3种工况下关键测点处的相对误差

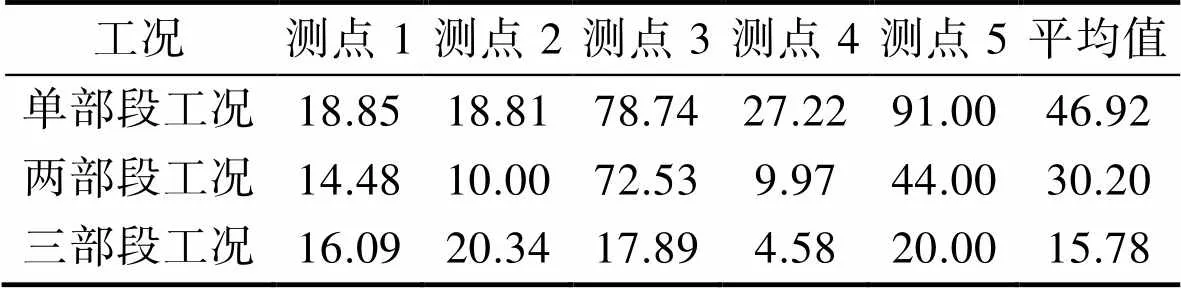
Tab.11 Relative error on key measuring points among three conditions %

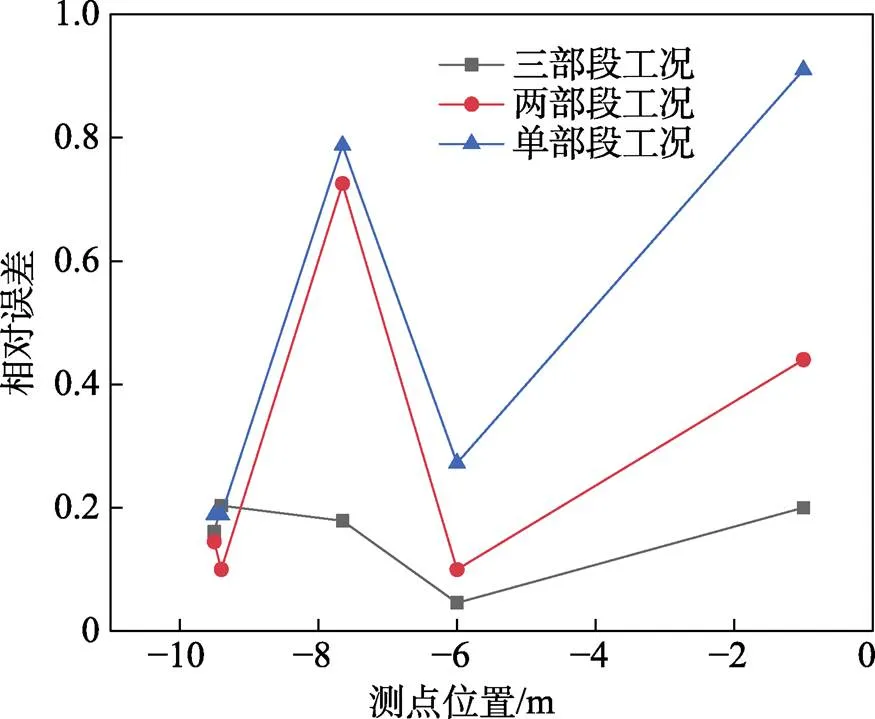
图14 3种工况下关键测点处加速度相对误差

3.2 安全性分析

由于基于螺栓连接法的三部段工况模型通过了模型校核，故使用该模型计算了水平跌落仿真中含能材料的应力响应。对比仿真结果与反应阈值，判断含能材料是否发生反应。计算了三部段工况下含能材料的应力最大值，见表12。其中，战斗部装药的Von Mises应力最大值约为6.4 MPa，小于B炸药反应阈值21.249 MPa，因此不会反应；发动机装药的Von Mises应力最大值约为3.1 MPa，小于HTPB推进剂反应阈值974.1 MPa，因此也不会反应。

表12 三部段工况下的含能材料应力最大值

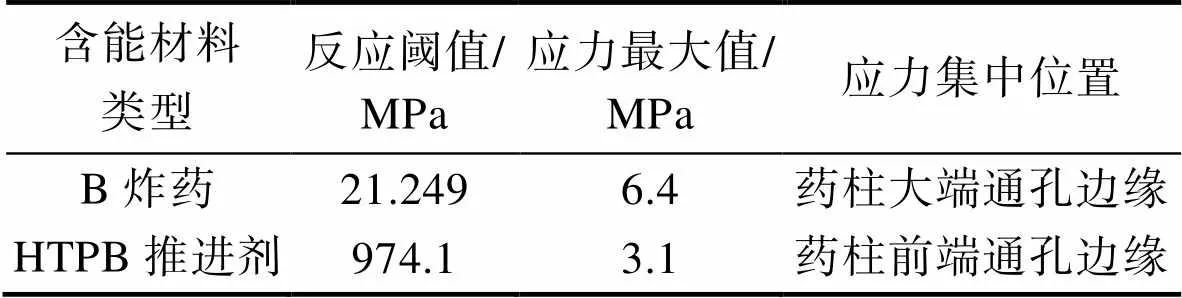
Tab.12 Maximum stress of energetic materials with 3-segment condition

4 结论

本文对固体导弹水平跌落进行数值仿真，研究了部段间螺栓连接的建模方法和断裂数量对全弹动力学响应的影响。使用位移、加速度实测值进行了模型校核，使用精度最高的全弹简化模型计算了全弹应力场。

1）不同的螺栓连接简化模型得到的全弹加速度响应具有显著差异。其中，壳体连接法、简支梁连接法、梁间连接法不能正确反映实际情况下螺栓连接结构的受力情况，因而无法准确计算全弹跌落过程中的回弹加速度；而使用螺栓连接法作为简化模型时得到的相对误差平均值最小，仅为15.78%。

2）螺栓断裂数量对于全弹的位移和加速度响应具有显著影响。不考虑螺栓断裂将无法准确计算全弹跌落过程中的回弹位移与加速度，位移误差平均值可达95 mm，相对误差平均值可达46.92%。三部段工况下的螺栓断裂数量与实际一致，且计算最为精确，各测点处的位移误差平均值仅17.5 mm，加速度相对误差平均值仅15.78%。

3）经过位移、加速度实测值校核，使用基于螺栓连接法的三部段工况模型计算全弹水平跌落的应力响应。水平跌落条件下，战斗部装药应力最大值6.4 MPa、小于反应阈值21.249 MPa；发动机装药应力最大值3.1 MPa，远小于反应阈值974.1 MPa。因此，6 m全弹水平跌落不会直接引起装药反应。通过全弹水平跌落试验证实了本文结论。

[1] 邓海, 李刚, 郭洪卫, 等. 不敏感弹药技术的发展现状与趋势[J]. 兵器装备工程学报, 2022, 43(2): 137-144. DENG Hai, LI Gang, GUO Hong-wei, et al. Development Status and Trend of Insensitive Ammunition Technology[J]. Journal of Ordnance Equipment Engineering, 2022, 43(2): 137-144.

[2] 蔡选义. ○一四中心进行导弹发动机跌落试验[J]. 航空兵器, 1991(3): 10. CAI Xuan-yi. 014 Center Conducts Missile Engine Drop Test[J]. Aero Weaponry, 1991(3): 10.

[3] 江明, 唐成, 袁宝慧. 导弹战斗部安全性试验评估[J]. 四川兵工学报, 2015, 36(7): 6-9. JIANG Ming, TANG Cheng, YUAN Bao-hui. Summary of Missile Warhead's Safety Tests Evaluation[J]. Journal of Sichuan Ordnance, 2015, 36(7): 6-9.

[4] 张学伦. 战斗部跌落安全性试验方法的述评[J]. 兵器装备工程学报, 2018, 39(7): 16-19. ZHANG Xue-lun. Review of Test Methods for Warhead Drop Safety[J]. Journal of Ordnance Equipment Engineering, 2018, 39(7): 16-19.

[5] 谢涛, 吕红超, 郝陈朋. 基于LS-DYNA的导弹战斗部跌落安全性分析[J]. 兵器装备工程学报, 2018, 39(8): 26-29. XIE Tao, LYU Hong-chao, HAO Chen-peng. Analysis on Drop Safety of Missile Warhead Based on LS-DYNA[J]. Journal of Ordnance Equipment Engineering, 2018, 39(8): 26-29.

[6] 杨明, 黄卫东, 李高春, 等. 舰载导弹固体发动机发射跌落危险性分析[J]. 海军航空工程学院学报, 2018, 33(4): 367-370. YANG Ming, HUANG Wei-dong, LI Gao-chun, et al. Launching Drop Risk Analysis of Shipborne Missile Solid Motor[J]. Journal of Naval Aeronautical and Astronautical University, 2018, 33(4): 367-370.

[7] 崔浩, 郭锐, 宋浦. 固体火箭发动机跌落安全性数值分析[J]. 兵工学报, 2018, 39(S1): 66-71. CUI Hao, GUO Rui, SONG Pu. Numerical Analysis of Safety of Solid Rocket Engine during Falling Process[J]. Acta Armamentarii, 2018, 39(S1): 66-71.

[8] 张斌, 李继承, 陈建良, 等. 构型弹体跌落冲击载荷及结构响应特性[J]. 爆炸与冲击, 2023, 43(3): 63-84. ZHANG Bin, LI Ji-cheng, CHEN Jian-liang, et al. Drop Impact Load and Structural Response Characteristics of Configuration Projectile[J]. Explosion and Shock Waves, 2023, 43(3): 63-84.

[9] 陈马旭, 乐贵高. 带泡沫缓冲的导弹跌落仿真[J]. 兵工自动化, 2014, 33(3): 34-35. CHEN Ma-xu, LE Gui-gao. Simulation of Missile Drop with Foam Cushions[J]. Ordnance Industry Automation, 2014, 33(3): 34-35.

[10] 白金泽. LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社, 2005. BAI Jin-ze. Theoretical Basis and Case Analysis of LS-DYNA3D[M]. Beijing: Science Press, 2005.

[11] 张策. 机械动力学[M]. 2版. 北京: 高等教育出版社, 2008. ZHANG Ce. Machinery Dynamics[M]. 2nd Ed. Beijing: Higher Education Press, 2008.

[12] 贾亚萍. 基于显式动力学有限元分析的叉车护顶架安全性能研究[D]. 杭州: 浙江大学, 2016. JIA Ya-ping. Research on safety Performance of Forklift Roof Guard Based on Explicit Dynamic Finite Element Analysis[D]. Hangzhou: Zhejiang University, 2016.

[13] 赵娟, 徐洪涛, 冯晓军. 装药条件对B炸药落锤撞击响应的影响研究[J]. 爆破器材, 2014, 43(6): 6-10. ZHAO Juan, XU Hong-tao, FENG Xiao-jun. Effects of Charge Conditions on the Drop Hammer Impact Response of Composition B[J]. Explosive Materials, 2014, 43(6): 6-10.

[14] 廖军, 代晓淦, 黄谦, 等. 药片落锤撞击试验中B炸药的响应特性[J]. 火炸药学报, 2013, 36(1): 52-54. LIAO Jun, DAI Xiao-gan, HUANG Qian, et al. Reaction Characteristic for Composition B in Drop Hammer Impact Sensitivity Test[J]. Chinese Journal of Explosives & Propellants, 2013, 36(1): 52-54.

[15] 李凯, 朱建生, 钱志博, 等. 基于J-C本构模型的Comp.B炸药落锤冲击数值模拟[J]. 力学与实践, 2011, 33(1): 21-23. LI Kai, ZHU Jian-sheng, QIAN Zhi-bo, et al. Numerical Simulation of Drop Weight Impact Tests for Comp.b Using johnson-Cook Constitutive Model[J]. Mechanics in Engineering, 2011, 33(1): 21-23.

[16] 袁俊明, 刘玉存, 曹文军. B炸药落锤撞击点火的数值模拟[J]. 含能材料, 2013, 21(1): 30-34. YUAN Jun-ming, LIU Yu-cun, CAO Wen-jun. Numerical Simulation of Drop Weight Impact Ignition on Composite Explosive[J]. Chinese Journal of Energetic Materials, 2013, 21(1): 30-34.

[17] 冯晓军, 封雪松, 赵娟, 等. 固体推进剂在低速撞击刺激下响应研究[C]// 第十六届中国科协年会——分9含能材料及绿色民爆产业发展论坛论文集. 昆明: [出版者不详], 2014. FENG Xiao-jun, FENG Xue-song, ZHAO Juan, et al. Chinese Association for Science and Technology, People's Government of Yunnan Province[C]// Proceedings of the 16th Annual Conference of the Chinese Association for Science and Technology—9th Forum on the Development of Energy Containing Materials and Green Civil Explosive Industries. Kunming: [s. n.], 2014

[18] 刘兆恒, 郁红陶, 刘卓. 落锤撞击下丁羟推进剂点火反应的数值模拟[J]. 弹箭与制导学报, 2022, 42(2): 89-93. LIU Zhao-heng, YU Hong-tao, LIU Zhuo. Numerical Simulation of Ignition Reaction of HTPB Propellant under Drop-Weight Impact[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2022, 42(2): 89-93.

[19] 刘兆恒. 低压冲击作用下HTPB固体推进剂点火反应研究[D]. 西安: 西安工业大学, 2022. LIU Zhao-heng. Study on Ignition Reaction of HTPB Solid Propellant under Low Pressure Impact[D]. Xi'an: Xi'an Technological University, 2022.

[20] HOLMQUIST T J, JOHNSON G R. Determination of Constants and Comparison of Results for Various Constitutive Models[J]. Le Journal De Physique IV, 1991, 1(C3): C3-853.

[21] WANG X B. Effects of Constitutive Parameters on Thickness of Phase Transformed Adiabatic Shear Band for Ductile Metal Based on Johnson-Cook and Gradient Plasticity Models[J]. Advanced Materials Research, 2006, 15-17: 609-614.

[22] KANG W J, CHO S S, HUH H, et al. Modified Johnson-Cook Model for Vehicle Body Crashworthiness Simulation[J]. International Journal of Vehicle Design, 1999, 21(4/5): 424.

[23] Livermore Software Technology Corporation. LS-DYNAR keyword user's manual[Z]. Livermore Software Technology Corporation, 2007.

[24] 辛春亮, 薛再清, 涂建, 等. 有限元分析常用材料参数手册[M]. 北京: 机械工业出版社, 2020: 38-247.

XIN Chun-liang, XUE Zai-qing, TU Jian, et al. Manual of Common Material Parameters in FEA[M]. Beijing: China Machine Press, 2020: 38-247.

[25] 许进升. 复合推进剂热粘弹性本构模型实验及数值仿真研究[D]. 南京: 南京理工大学, 2013. XU Jin-sheng. Experimental and Numerical Simulation Study on Thermoviscoelastic Constitutive Model of Composite Propellant[D]. Nanjing: Nanjing University of Science and Technology, 2013.

[26] 徐一航, 李道奎, 周仕明, 等. 基于并行流变框架HTPB推进剂本构模型研究[J]. 推进技术, 2022, 43(9): 403-410. XU Yi-hang, LI Dao-kui, ZHOU Shi-ming, et al. HTPB Propellant Constitutive Model Based on Parallel Rheological Framework[J]. Journal of Propulsion Technology, 2022, 43(9): 403-410.

[27] GB 50010—2010, 混凝土结构设计规范[S]. GB 50010—2010, Code for Design of Concrete Structures[S].

[28] CHEN Yan, GAO Qiang, GUAN Zhen-qun. Self-Loos­ening Failure Analysis of Bolt Joints under Vibration Considering the Tightening Process[J]. Shock and Vibration, 2017, 2017: 1-15.

[29] 田彤辉. 箭(弹)级间螺栓法兰连接结构失效实验与数值仿真研究[D]. 长沙: 国防科技大学, 2018. TIAN Tong-hui. Experimental and Numerical Simulation Study on Failure of Bolt-Flange Connection Structure between Rocket and Projectile Stages[D].Changsha: National University of Defense Technology, 2018.

[30] 王青文. 瞬态冲击下螺栓法兰连接结构失效研究[D]. 长沙: 国防科技大学, 2017. WANG Qing-wen. Study on Failure of Bolted Flange Connection Structure under Transient Impact[D]. Changsha: National University of Defense Technology, 2017.

Assessment of Solid Fuel Missile Safety in Horizontal Drop Test Involving Bolt Failure

WU Zhen-yu1, ZHANG Tao1,2*

(1. School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China; 2.State Key Laboratory of Structural Analysis, Optimization and CAE Software for Industrial Equipment, Dalian University of Technology, Liaoning Dalian 116024, China)

The solid fuel missile safety in horizental drop test was assessed through numerical simulation. The 6m drop test of solid fuel missile with main axis at horizontal orientaion was simulated using LS-DYNA. The numerical model was verified with displacement and acceleration test data. Stress field was calculated based on the verified model to indicate whether energetic metarials would be ignited. Results from different bolt joint model and different quantities of bolt with failure were compared. It demonstrates that the bolt connection method has the highest accuracy when calculating the peak acceleration among all the modeling methods; the 3-segment condition generates the the most accurate quantity of bolt with failure and peak acceleration numerical solution. According to the most accurate numerical model, the maximum Von Mises stress inside the warhead and engine are both less than the reaction threshold. In conclusion, it is found that the modeling method and quantity of bolt with failure have a significant effect on the calculation accuracy of displacement and acceleration. The most reliable simulation results are obtained by the 3-segment condition and using the bolt connection method for modeling. The stress field result based on the most accurate numerical model indicates that a 6-meter horizontal drop of the entire missile will not directly cause the ignition reaction in the warhead and engine.

finite element analysis; horizontal drop; bolt joint; bolt failure; energetic materials; ammunition safety

2023-08-01；

2023-09-21

Open Fundation State Key Laboratory of Structural Analysis, Optimization and CAE Software for Industrial Equipment, Dalian University of Technology (GZ23118)

TJ760.6

A

1672-9242(2023)10-0090-11

10.7643/ issn.1672-9242.2023.10.011

2023-08-01；

2023-09-21

大连理工大学工业装备结构分析优化与 CAE 软件全国重点实验室基金（GZ23118）

吴振宇, 张韬. 考虑螺栓断裂的固体导弹水平跌落安全性分析[J]. 装备环境工程, 2023, 20(10): 90-100.

WU Zhen-yu, ZHANG Tao. Assessment of Solid Fuel Missile Safety in Horizontal Drop Test Involving Bolt Failure[J]. Equipment Environmental Engineering, 2023, 20(10): 90-100.

责任编辑：刘世忠