考虑延缓纠正的双应力加速可靠性增长试验方法

邢浩，杨军

专刊——导弹武器贮存延寿

考虑延缓纠正的双应力加速可靠性增长试验方法

邢浩，杨军

（北京航空航天大学 可靠与系统工程研究院，北京 100191）

缩短传统加速可靠性增长试验时间，以及考虑延缓纠正方式对产品可靠性的影响。提出考虑延缓纠正的双应力加速可靠性增长试验方法，首先，采用基于延缓纠正AMSAA模型跟踪可靠性增长过程，并采用极大似然估计方法估计模型参数；其次，以温度和振动作为加速应力为例，开展加速寿命试验，获得试验数据，基于广义艾琳模型，通过最小二乘估计方法得到加速系数；然后，将产品可靠性外推到正常应力水平。航空蓄电池应用案例分析表明，与基于单应力加载的高应力加速可靠性增长试验相比，所提方法能够缩短29.4%的试验时间，并且采用延缓纠正方式对产品的可靠性有影响。为产品在双应力加载方式和采用延缓纠正方式下开展高应力加速可靠性增长试验的可靠性评估提供了技术手段。

双应力；加速可靠性增长；AMSAA模型；广义艾琳模型；加速系数；延缓纠正文

可靠性增长试验是通过对产品施加真实的或模拟的环境应力，揭示产品的故障，并采取纠正措施，从而提高产品的可靠性，使其达到预定要求的一种试验。它是一个有计划的试验—分析—改进过程，其目的是对暴露的问题采取有效的纠正措施，从而达到预定的可靠性增长目标，是提高产品可靠性的有效方法之一[1-6]。然而，随着科学技术的发展，许多可修系统，如动力装置[7]、控制仪表[8]、航空航天部件[9]等，在可靠性增长试验前具有较高的可靠性，其故障间隔时间长，在正常应力下开展可靠性增长试验周期长，成本高。为了有效地解决这一问题，将加速寿命试验[10-13]思想引入到可靠性增长试验中，得到了加速可靠性增长试验方法。通过施加比正常应力更严酷的应力，加速产品的失效，然后进行相应的分析和纠正，实现产品可靠性的快速增长。

在过去几十年，加速可靠性增长试验得到了大力发展[14-23]。Yu等[14]在Cox的加速寿命模型和Duane可靠性增长模型的基础上，提出了一种加速可靠性增长模型。Acevedo等[15]对加速寿命试验进行了回顾，发现执行良好的加速寿命试验是实现产品可靠性增长的有效方法。周源泉等[16]基于Arrhenius和逆幂律模型，给出了恒应力加速可靠性增长试验中单个失效时间数据的统计分析方法。Ye等[17]基于AMSAA- BISE模型和广义艾琳模型，提出了双应力加速可靠性增长试验方法。Feinberg[18]研究了单应力和多应力水平可靠性增长寿命数据的卡方加速可靠性增长模型。Ruiz等[19]提出了一种贝叶斯加速可靠性增长方法，采用分块分解技术对部件的加速寿命试验数据进行聚合，估计产品的可靠性。Ruiz等[20]提出了一种贝叶斯框架来分析可靠性增长中的加速寿命试验数据。Anand等[21]在加速可靠性增长试验的基础上，提出了一种进行磁共振成像系统可靠性试验的方法。Ruiz等[22]提出了一种在加速可靠性增长计划中利用退化数据进行系统可靠性预测的模型。Ruiz等[23]提出了一种贝叶斯选择加速可靠性增长方法来加速潜在失效模式的发生。

然而，上述研究大多集中在单加速应力下进行加速可靠性增长试验上，而且在低加速应力水平下开展加速可靠性增长试验时间过长，工程上难以接受。此外，在采用延缓纠正方式下，由于失效没有立即纠正，因此在试验结束时，采取延缓纠正将影响产品的可靠性。因此，为了更有效地缩短试验时间，并考虑延缓纠正对产品可靠性的影响，本文提出了一种考虑延缓纠正的双应力加速可靠性增长试验方法。首先，利用AMSAA模型跟踪最高加速应力水平组合下的可靠性增长过程。其次，以温度和振动为加速应力，在不同应力水平组合下进行加速寿命试验，得到加速寿命试验数据，基于广义Eyring模型，通过最小二乘估计法得到加速系数。然后，结合加速系数，将试验结束时的产品可靠性外推到正常应力水平。最后，以航空蓄电池为例，验证了所提方法的有效性。本文针对单加速应力下加速可靠性增长试验时间过长的问题，提出了双应力加载方式下的高应力加速可靠性增长试验方法，在最高加速应力水平组合下进行可靠性增长试验，更有效地缩短试验时间。另外，由于采取即时修正会占用产品较长时间，因此提出在高应力加速可靠性增长试验中采用延缓纠正的方式，并考虑延缓纠正对产品可靠性的影响。

1 模型建立

1.1 基本假设

在进行延缓纠正的双应力加速可靠性增长试验方法之前，需要给出7个假设。基于文献[24]，给出假设1～4来描述试验中故障分类、针对故障采取的纠正方式以及故障模式和失效数服从的分布。根据工程实际和文献[16]，给出假设5去描述可靠性如何增长，假设6去描述产品失效机理不发生改变。基于文献[10]，给出假设7来描述加速系数。

假设1[24]。故障模式可分为A类故障和B类故障，且故障模式彼此独立，任何故障发生都会导致系统故障。

假设2[24]。对于潜在的B类故障，一些B类故障采取即时纠正方法，其余的B类故障则采取延缓纠正方法。

假设3[24]。发现的B类失效模式的数目服从非齐次泊松过程，其均值函数为幂函数。

假设4[24]。试验段中，持续试验时间的每一个A类失效模式下的失效数目和每一个B类失效模式下的失效数目均为齐次泊松过程。

假设5[16]。在最高的加速应力水平组合下，采取纠正措施后，产品的可靠性显著提高。

假设6[16]。在正常及加速应力水平S下，产品故障机理不变的条件为：过程的某个参数或过程的某些参数的函数不随S的变化而异。

假设7[10]。在正常应力水平0下，产品的失效分布函数为0()，t,0为产品达到失效率的时间，也就是0(t,0)=；在正常应力水平S下，产品的失效分布函数为F()，t,i为产品达到失效率的时间，也就是0(t,i)=，则加速应力水平S对于正常应力水平0的加速系数为：

1.2 加速可靠性增长模型

1）加速寿命模型。本节以温度和振动作为加速应力为例，产品的特征寿命与加速应力水平之间的关系满足广义艾林模型。对于双应力情况，采用温度和非温度应力同时作用于加速寿命试验：

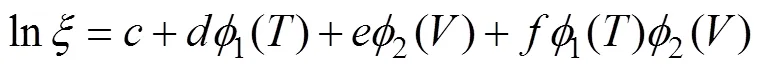
2）可靠性增长模型。为考虑采用延缓纠正方式对系统可靠性的影响，本节采用基于延缓纠正AMSAA模型作为可靠性增长模型。模型原理：该模型相关参数估计过程用来评估延缓纠正对产品可靠性的影响。特别是，在第二试验阶段之前，模型和估计过程可以评估系统在采取延缓纠正后的故障强度。失效强度表示为()，其中表示第一阶段的试验时间。该模型对()的估计基于：从试验阶段获得A、B类失效的失效数据；在试验阶段发现的B类失效的d估计值。

在第一试验阶段，没有采取纠正措施的产品的失效强度为：

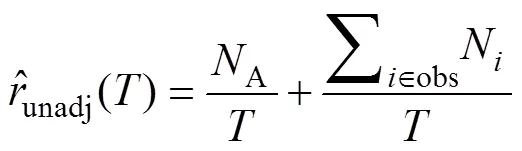
式中：obs为试验段发生的所有B类失效构成的集合。

纠正过程估计()的基础是试验段内的B类失效模式的失效数由N减少到(1－d)N，其中d是对失效模式的实际估计。纠正过程对()的估计为：

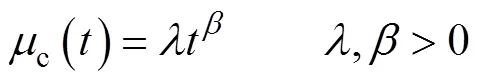
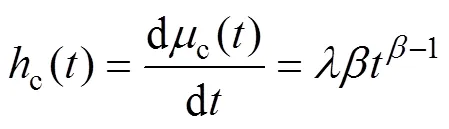
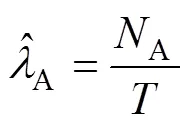
式中：A为[0,]内的A类失效数。

根据假设4，所有的纠正都推迟到试验段结束后，B类失效模式的失效率在[0,]内保持恒定，估计值为：

式中：N表示[0,]内B类失效模式的失效数。

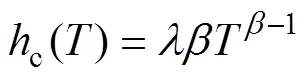
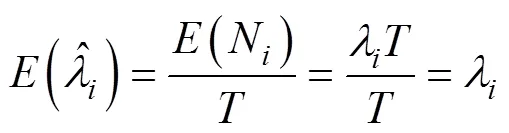
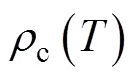
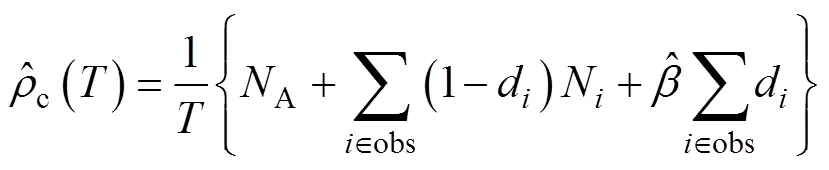
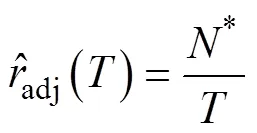
根据式（15）可以得到：

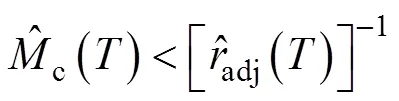
1.3 多应力加速可靠性增长模型参数估计

对式（17）两边分别取对数，得：

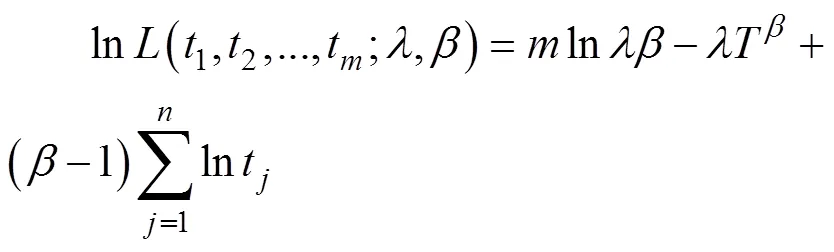
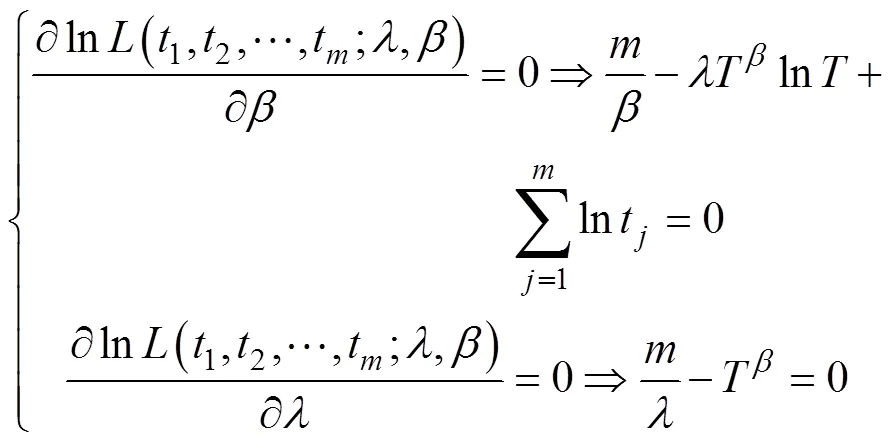
然后得到模型的极大似然估计值：

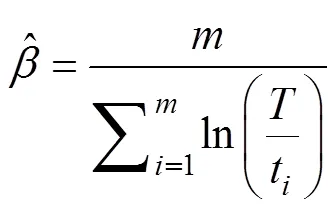
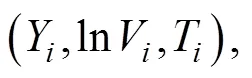
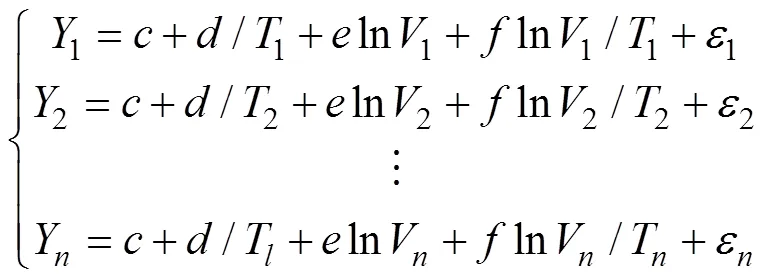
将式（22）转换成矩阵形式：

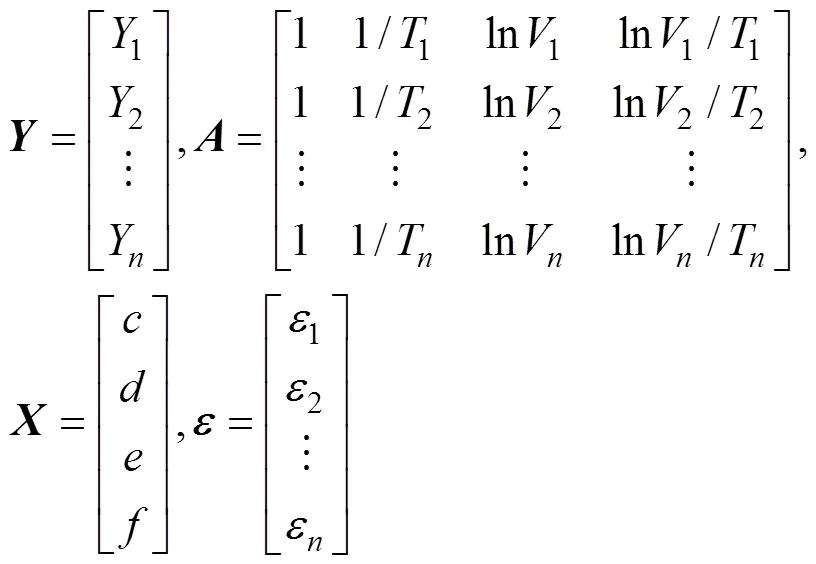
式（22）可以重新写为：

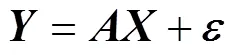
通过最小二乘估计方法估计的参数，能够使得偏差平方和达到最小值min：

则参数结果估计为：

因此，4个参数估计结果为：

2 结果及分析

航空蓄电池作为飞机发动机的起动电源，其可靠性水平的高低直接影响航空产品的使用，因此本节以航空蓄电池为例（如图1所示），阐述了所提出方法的有效性，给出了高应力水平组合下的加速可靠性增长试验方法。根据产品的特性，首先给出加速应力和水平大小。选择温度和振动作为加速应力，每种应力都有4个水平，见表1。温度的正常水平为0=298 K，振动的正常水平为0=0.032/Hz。通过均匀设计，应力水平组合见表2。

图1 航空蓄电池

表1 环境应力与水平大小

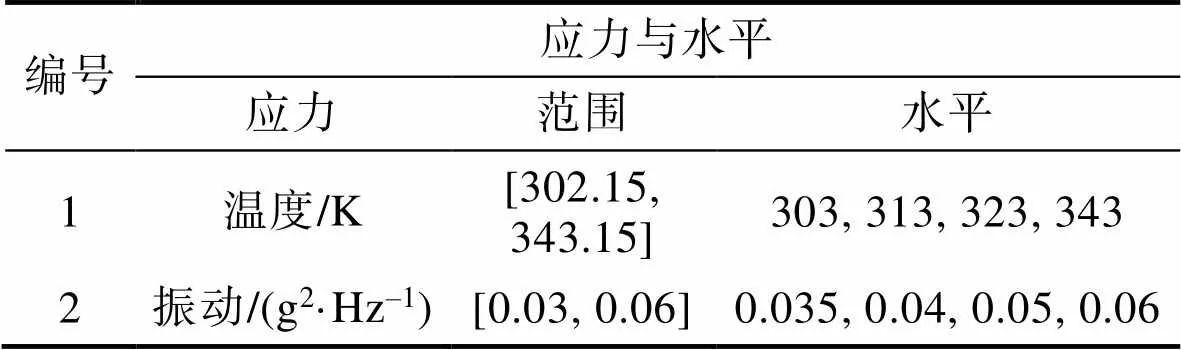
Tab.1 Environment stress and level

表2 均匀设计下应力组合

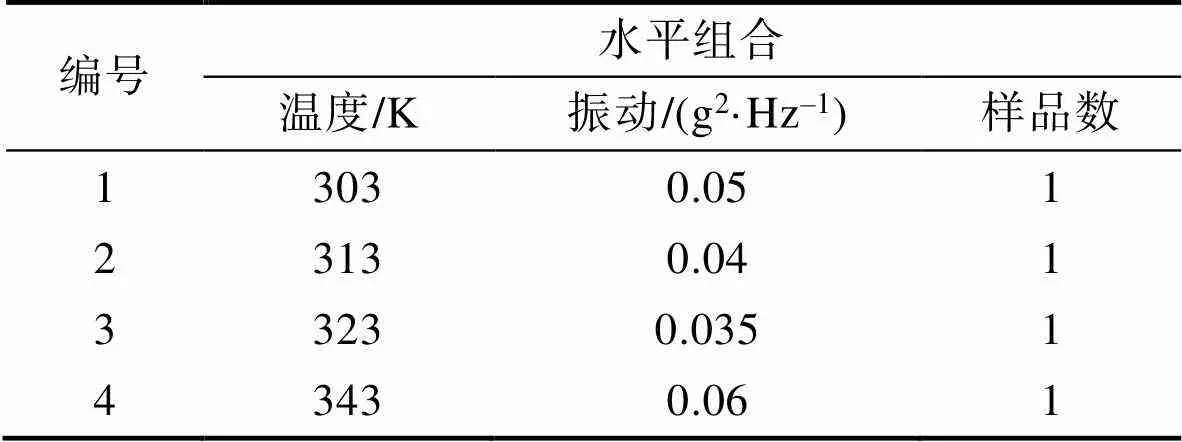
Tab.2 Stress combinations by uniform design

2.1 加速寿命试验

根据实际工程背景，航空航天电子产品的特征寿命为11 000 h，该产品的目标MTBF为18 000 h。目前产品处于工程研制阶段，在高应力加速可靠性增长试验前进行了4组可靠性试验，加速寿命试验在4种应力水平组合下同步进行，该产品的特征寿命分别为10 000、8 500、6 500、4 500 h。

加速寿命方程的最小二乘估计为=19.3，=－3 264.7，=5.7，=－1 788.1。然后由式（1）和式（2），计算得出正常应力条件下产品的特征寿命和加速系数，见表3。

表3 4组应力水平下的特征寿命与加速系数

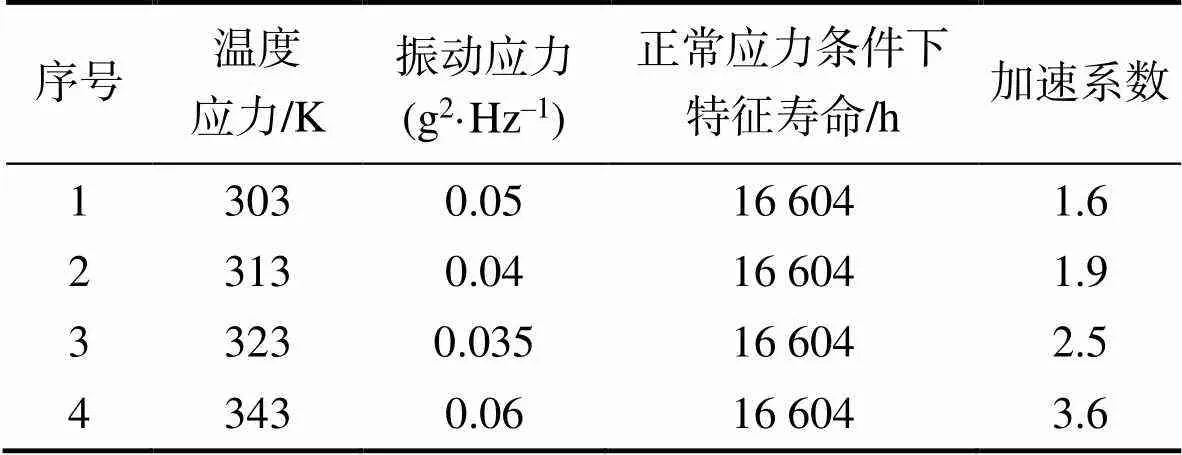
Tab.3 Characteristic life and acceleration coefficient under four stress combinations

2.2 高应力水平组合下的可靠性增长试验

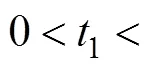
表4 第一阶段B类失效试验数据

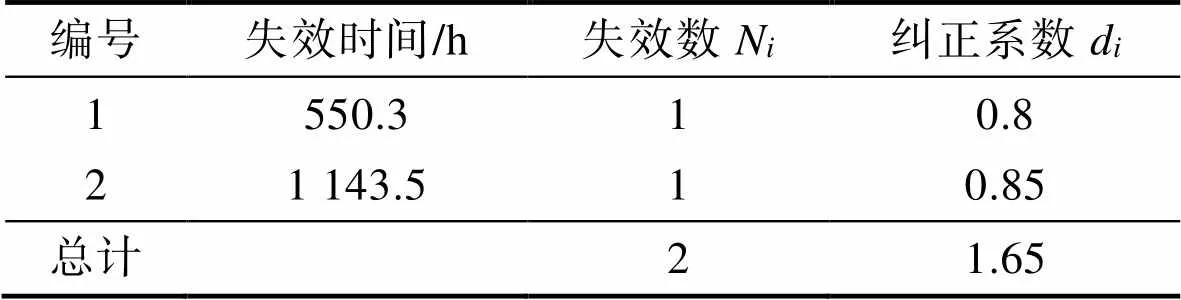
Tab.4 Test data of B failure in the first test phase

采取延缓纠正前，产品的失效率为：

相应的产品的MTBF值（MTBF）为：

在第一阶段末采取延缓纠正后，产品的失效率为：

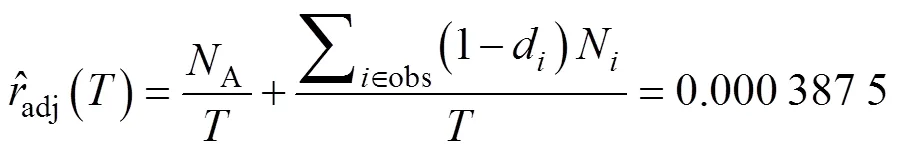
相应的产品MTBF值为：

在第一试验阶段结束时进行纠正后，产品失效率的预期值为：

在第一试验阶段结束时进行纠正后产品的MTBF值为：

第二试验阶段的截尾失效时间为=6 000 h。B类失效的试验数据见表5。

表5 第二阶段B类失效试验数据

Tab.5 Test data of B failure in the second test phase

采取延缓纠正前，产品的失效率为：

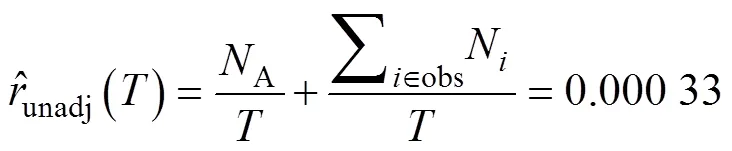
相应的产品MTBF值为：

在第二阶段末采取延缓纠正后，产品的失效率为：

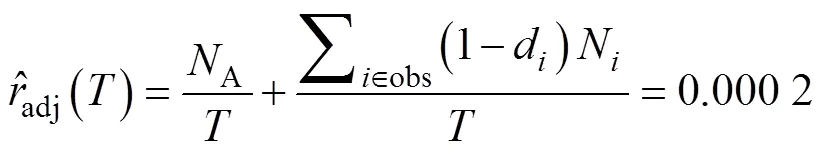
相应的产品MTBF值为：

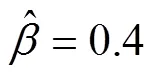
在第二试验阶段结束时进行纠正后，产品失效率的预期值为

在第二试验阶段结束时进行纠正后产品的MTBF值为：

第二试验阶段的截尾失效时间为=8 000 h，B类失效的试验数据见表6。

表6 第二阶段B类失效试验数据

Tab.6 Test data of B failure in the third test phase

采取延缓纠正前，产品的失效率为：

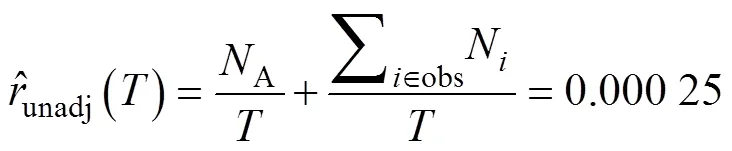
相应的产品MTBF值为：

在第三阶段末采取延缓纠正后，产品的失效率为：

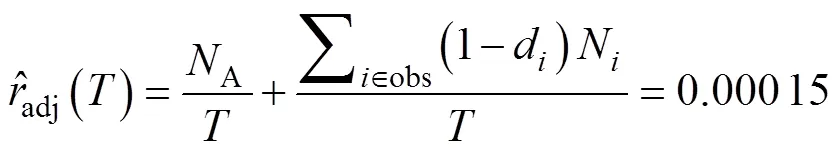
相应的产品MTBF值为：

在第三试验阶段结束时进行纠正后，产品失效率的预期值为：

在第三试验阶段结束时进行纠正后，产品的MTBF值为：

外推到正常条件下产品的MTBF值为：

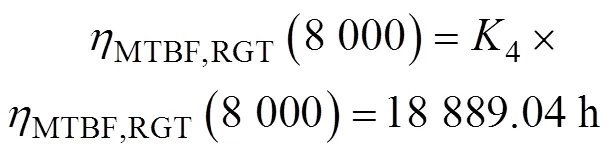
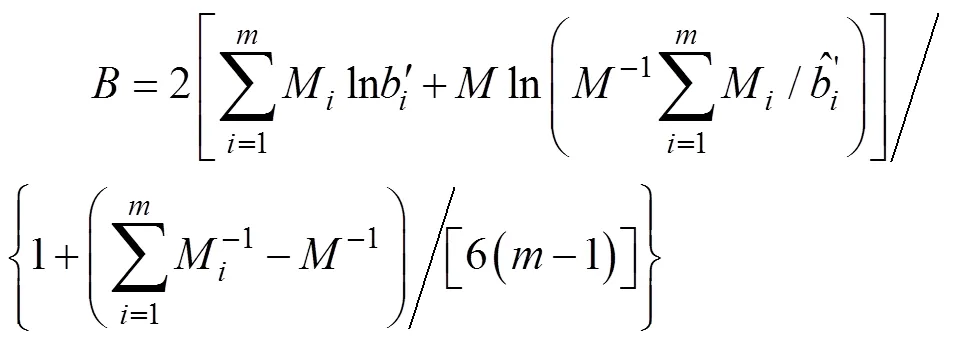
为验证AMSAA模型的合理性，本文使用克莱默- 冯-米塞斯方法[26]。

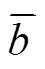
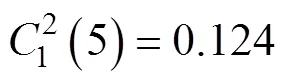
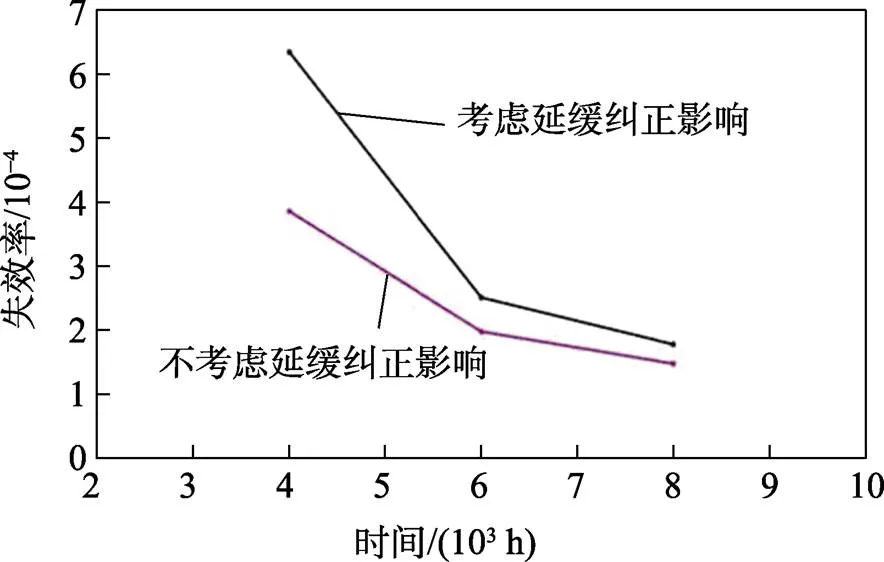
图2 产品失效率

将单应力下的高应力加速可靠性增长试验方法与所提方法进行对比，结果见表7。从表7可以看出，当可靠性增长目标值为18 000 h时，高应力加速可靠性增长试验在单应力下所需的总试验时间为10 359.7 h，而所提方法所需的总试验时间为8 000 h。因此，本文所提方法节省了更多的试验时间，效果明显。

表7 所提方法与单应力高加速可靠性增长试验比较

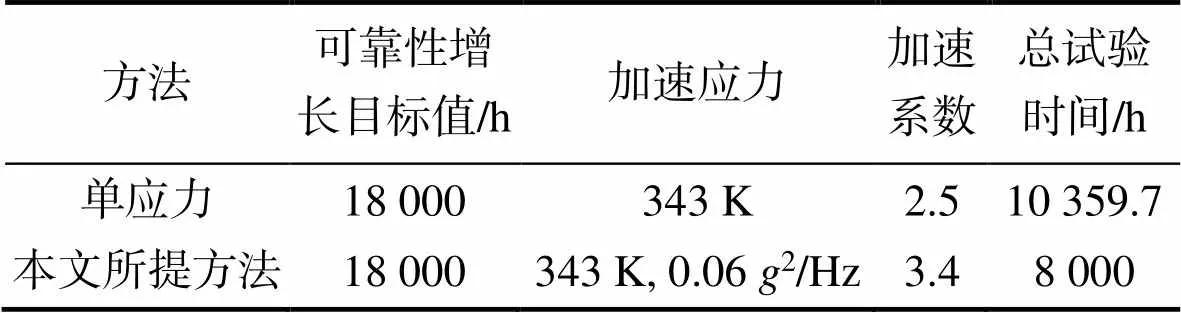
Tab.7 Comparison between HARGT under single-stress and the proposed method

3 结论

1）通过采用双应力加载方式下的高应力加速可靠性增长试验，验证了所提方法的有效性。试验结果对比表明，所提方法比单应力加载方式能够节省29.4%的试验时间，效果更显著。

2）采用延缓纠正方式的确对产品的可靠性有影响，因此在实际工程中，应该采取合适的纠正措施，更加有效地提高产品服役时间。

[1] AWAD M. Economic Allocation of Reliability Growth Testing Using Weibull Distributions[J]. Reliability Engineering & System Safety, 2016, 152: 273-280.

[2] XU J Y, YU D, XIE M, et al. An Approach for Reliability Demonstration Test Based on Power-Law Growth Model[J]. Quality and Reliability Engineering Interna­tional, 2017, 33(8): 1719-1730.

[3] LI Zhao-jun, MOBIN M, KEYSER T. Multi-Objective and Multi-Stage Reliability Growth Planning in Early Product-Development Stage[J]. IEEE Transactions on Reliability, 2016, 65(2): 769-781.

[4] BYUN J E, NOH H M, SONG J. Reliability Growth Analysis ofSystems Using Matrix-Based System Reliability Method[J]. Reliability Engineering & System Safety, 2017, 165: 410-421.

[5] HEYDARI M, SULLIVAN K M. An Integrated Approach to Redundancy Allocation and Test Planning for Reliability Growth[J]. Computers & Operations Research, 2018, 92: 182-193.

[6] CROW L H. Reliability Growth Projection from Delayed Fixes[C]// Proceedings of RAMS 1983 Symposium. New York:Newman Laboratory of Nuclear Studies, 1983.

[7] CHOI U M, JØRGENSEN S, BLAABJERG F. Advanced Accelerated Power Cycling Test for Reliability Investigation of Power Device Modules[J]. IEEE Transac­tions on Power Electronics, 2016, 31(12): 8371- 8386.

[8] YANG Ya-guang, RUSSELL S. Reliability Estimation for a Digital Instrument and Control System[J]. Nuclear Engineering and Technology, 2012, 44(4): 405-414.

[9] KUMAR B P, KUMAR C, KUMAR V S, et al. Reliability Considerations of Spherical Phased Array Antenna for Satellites[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(3): 1381-1391.

[10] COLLINS D H, FREELS J K, HUZURBAZAR A V, et al. Accelerated Test Methods for Reliability Prediction[J]. Journal of Quality Technology, 2013, 45(3): 244-259.

[11] WANG Liang. Estimation of Constant-Stress Accelerated Life Test for Weibull Distribution with Nonconstant Shape Parameter[J]. Journal of Computational and Applied Mathematics, 2018, 343: 539-555.

[12] ABDEL GHALY A A, ALY H M, SALAH R N. Different Estimation Methods for Constant Stress Accelerated Life Test under the Family of the Exponentiated Distributions[J]. Quality and Reliability Engineering International, 2016, 32(3): 1095-1108.

[13] NASSAR M, DEY S. Different Estimation Methods for Exponentiated Rayleigh Distribution under Constant- Stress Accelerated Life Test[J]. Quality and Reliability Engineering International, 2018, 34(8): 1633-1645.

[14] YU T, SONG B, FENG Y, et al. Research on Accelerated Reliability Growth Model (ARGM) in Constant Stress [C]// Asia Pacific Symposium on Safety 2005. Shaoxing: COSHA, 2005: 1991-1996.

[15] ACEVEDO P E, JACKSON D S, KOTLOWITZ R W. Reliability Growth and Forecasting for Critical Hardware through Accelerated Life Testing[J]. Bell Labs Technical Journal, 2006, 11(3): 121-135.

[16] 周源泉, 朱新伟. 论加速可靠性增长试验(Ⅴ)单独故障时间数据的统计方法[J]. 推进技术, 2001, 22(4): 265- 268. ZHOU Yuan-quan, ZHU Xin-wei. Research on Acce­lerated Reliability Growth Testing (V)Statistical Methods for Individual Failure Time Data[J]. Journal of Propulsion Technology, 2001, 22(4): 265-268.

[17] YE Yan-qing, JIANG Jiang, LIU Qi, et al. Accelerated Reliability Growth Test under Multiple Environment Stresses[C]// 2013 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE). Chengdu: IEEE, 2013.

[18] FEINBERG A. Chi-Squared Accelerated Reliability Growth Model[C]// 2013 Proceedings Annual Reliability and Maintainability Symposium (RAMS). Orlando: IEEE, 2013.

[19] RUIZ C, LIAO Hai-tao, POHL E, et al. Bayesian Accele­rated Reliability Growth of Complex Systems[C]// 2018 Annual Reliability and Maintainability Symposium (RAMS). Reno: IEEE, 2018.

[20] RUIZ C, POHL E, LIAO Hai-tao, et al. A Bayesian Framework for Accelerated Reliability Growth Testing with Multiple Sources of Uncertainty[J]. Quality and Reliability Engineering International, 2019, 35(3): 837- 853.

[21] ANAND, SHIN, SAXENA, et al. Accelerated Reliability Growth Test for Magnetic Resonance Imaging System Using Time-of-Flight Three-Dimensional Pulse Sequence [J]. Diagnostics, 2019, 9(4): 164.

[22] RUIZ C, LIAO Hai-tao, POHL E A. Analysis of Correlated Multivariate Degradation Data in Accelerated Reliability Growth[J]. Quality and Reliability Engineering International, 2021, 37(7): 3125-3144.

[23] RUIZ C, HEYDARI M, SULLIVAN K M, et al. Data Analysis and Resource Allocation in Bayesian Selective Accelerated Reliability Growth[J]. IISE Transactions, 2020, 52(3): 301-320.

[24] MIL-HDBK-189-1981, Reliability Growth Management[S].

[25] 史全林, 周源泉. 多台系统幂律过程参数的比较[J]. 质量与可靠性, 2000(1): 31-34. SHI Quan-lin, ZHOU Yuan-quan. Comparison of Power Law Process Parameters of Multiple Systems[J]. Quality and Reliability, 2000(1): 31-34.

[26] ZHANG Jiu-jun, LI Er-jie, LI Zhong-hua. A Cramér-von Mises Test-Based Distribution-Free Control Chart for Joint Monitoring of Location and Scale[J]. Computers & Industrial Engineering, 2017, 110: 484-497.

A Double Stress Accelerated Reliability Growth Test with Delayed Corrections

XING Hao, YANG Jun

(School of Reliability and Systems Engineering, Beihang University, Beijing, 100191)

The work aims to shorten the time of traditional accelerated reliability growth tests and consider the effect of de­layed corrections on product reliability. A double-stress accelerated reliability growth test method considering delayed correc­tions was proposed. Firstly, the reliability growth process was tracked with the AMSAA model based on delayed correction, and the model parameters were estimated by the maximum likelihood estimation method. Secondly, with temperature and vibration as the accelerated stress, an accelerated life test was carried out to obtain the test data, and the acceleration coefficient was ob­tained by the least square estimation method based on the generalized eyring model. Then, the product reliability was extrapo­lated to normal stress level. The application case analysis of aircraft storage battery showed that the proposed method could shorten the test time by 29.4% compared with the high-stress accelerated reliability growth test based on single-stress loading and the delayed corrections method had an impact on the product reliability. It provides technical methods for reliability evalua­tion of high-stress accelerated reliability growth tests under double-stress loading and delayed corrections.

double-stress; accelerated reliability growth; AMSAA model; generalized eyring model; acceleration coeffi­cient; delayed corrections

2023-09-14；

2023-09-25

The National Natural Science Foundation of China (72371008, 71971009)

TJ089

A

1672-9242(2023)10-0001-07

10.7643/ issn.1672-9242.2023.10.001

2023-09-14；

2023-09-25

国家自然科学基金（72371008，71971009）

邢浩，杨军. 考虑延缓纠正的双应力加速可靠性增长试验方法[J]. 装备环境工程, 2023, 20(10): 001-007.

XING Hao, YANG Jun. A Double Stress Accelerated Reliability Growth Test with Delayed Corrections[J]. Equipment Environmental Engineering, 2023, 20(10): 001-007.

责任编辑：刘世忠