基于优化神经网络的采集终端软件可靠性预测

董永乐,毛永梅,张理放,张帆,白露薇,林海军,梁肇聪

(1.内蒙古电力科学研究院,呼和浩特 010000; 2.哈尔滨理工大学,哈尔滨 150080 )

0 引 言

随着智能电网建设在我国的深入开展,智能仪器、设备及综合测量控制管理系统在电力系统中得到广泛应用。由于智能电网对可靠性的要求非常高,所以对这些仪器、设备及系统的软件、硬件的可靠性就提出了更高的要求。由于硬件集成度不断提高,加之对硬件可靠性的研究投入大且成果比较丰富,相较于硬件,软件可靠性的研究成为制约采集终端等仪器设备可靠性的关键问题,也是可靠性研究的焦点之一。智能电网是关系到国计民生的重要系统,电网数据采集终端作为智能电网的关键设备,其可靠性直接影响着智能电网自动化系统的可靠性,因此,以采集终端为切入点,开展软件可靠性预测方法研究具有十分重要科学和现实意义。

从1967年Hudson提出了生灭过程模型开始,软件可靠性预测模型研究受到关注,之后,学者们提出了几十种软件可靠性模型,如J-M 模型、MUSA执行时间模型及贝叶斯排错模型等[1]。这些模型在一些分析软件中得到应用,但由于假设前提高且各异,对同一软件的评价结果迥异,影响了评价的公信力。

针对软件可靠性预测,科研人员建立了多种模型[2-7]。研究证明,预测效果较好的是基于分类思想的模型[8]。支持向量机[9]及神经网络理论[10-13]的研究成为热点,用于软件可靠性预测的神经网络有BP神经网络、LVQ神经网络及小波神经网络等[14]。但它们在应用中还是存在瑕疵。

例如,LVQ神经网络神经元利用不充分及算法对初值敏感等;隐层节点数难定、收敛速度较慢、易陷入局部最优解等问题困扰着小波神经网络,后两个问题也同样困扰着BP神经网络。为此,研究者提出了一些解决方案,以期得到更好的识别效果,例如提出了采用改进遗传算法AGA改进LVQ神经网络,用粒子群算法优化模糊神经网络等。

为了提高BP网络收敛速度和全局寻优能力,提高软件可靠性预测模型的预测能力,文章从完善SA和GA优化算法入手,给出改进的退火遗传融合优化算法MSAGA,进而提出一种基于MSAGA-BP神经网络的软件可靠性预测模型,即利用BP神经网络建立软件可靠性预测模型,用MSAGA优化网络参数,提高训练速度、全局寻优能力和精度,最后,应用该方法对采集终端进行软件可靠性预测模型建模分析,实现对该软件可靠性的预测。

1 SAGFA-BP神经网络

优化算法种类繁多,它们各有所长,各有所短,如果能取长补短则能收到更好的效果。在互补性分析,及完善算法的基础上,文中将遗传算法融合到退火算法中,提出退火遗传融合算法,并用它解决BP神经网络的优化问题。

1.1 GA的抗早熟改进

遗传算法(GA)是模仿生物进化的优化算法。GA虽然理论上可以搜索到最优解,但受杂交算子的影响,也有可能陷入局部最优。研究表明,种群的多样度高有助于全局搜索[15]。为了抗早熟,文中在判断接受新个体时,把适应度和多样度共同作为影响指标。

设种群Y用矩阵表示为:

(1)

若矩阵中非全1和非全0的列有m个,则Y的多样度为:

μ(Y)=m

(2)

另外,对种群Y来说,其总体适应度Fs(Y)等于个体适应度的最大值。即:

(3)

文中对GA的新个体接受进行改进,其它流程不变。判断接受时,先产生[0,1]上均匀分布随机数α,然后以下式接受新一代个体:

(4)

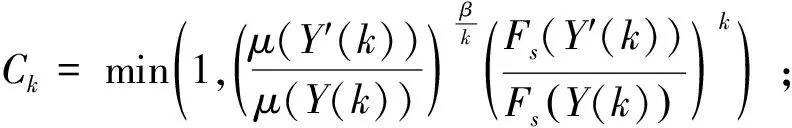
1.2 SA加速收敛方法

模拟退火(SA)算法是参考热力学退火过程的优化算法。它全局寻优能力强,但耗时较长。为提高其效率,一方面,在确定初始温度时,考虑最差的初始接受概率[16];另一方面,采取自寻优的方法[17]确定尺度。

为了防止初始温度选择得太高或者太低延缓SA收敛速度,选择下式确定:

t0=(fmin-fmax)/lnpr

(5)

式中pr为最差概率;fmax和fmin分别为目标函数的极大值和极小值。

SA算法退火时,新状态是通过在老状态的基础上,按照一定的尺度h随机增加扰动实现的。方法如图1所示。

x′(i)=x(i)+h·δ

(6)

1.3 融合优化算法SAGFA

针对GA和SA的优化质量和效率偏低的问题,文中提出退火遗传融合优化算法(simulated annealing genetic fusion algorithm,SAGFA),该算法在上述算法改进的基础上,通过互补融合,使新算法既具备GA的并行搜索能力,也兼具SA的概率突跳性,实现了高效与优质寻优的目标。SAGFA流程图如图2所示。

图2 SAGFA算法流程图

流程图中需要说明的是:

1)选用适应度函数作为SAGFA的评价函数,寻优方向是增大;

2)初始温度t0根据前面给出的式(5)确定;

3)采取指数下降策略;

4)按式(6)及图1的流程进行扰动;

5)个体取舍时,若新状态的适应度变大,则接收新状态,否定依据Metropolis准则,按概率接收新个体;

6)交叉时,为了保护优秀个体,依据下式自适应调节交叉率:

(7)

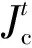
文中利用普遍使用的有代表性的6个标准函数[18]的极值搜索进行仿真,分别用SA、GA和SAGFA三种算法对6个函数搜索极小值,取搜索到全局最优解(最优解绝对误差小于10-5即认为搜索成功)20次的平均搜索时间(单位:s)列于表1。

表1 三种算法仿真结果

仿真结果表明:在同样搜索到全局最优的情况下,SAGFA较遗传算法和模拟退火算法具有更好的搜索速度。

1.4 SAGFA-BP神经网络

如前所述,多种神经网络各有不足。BP神经网络是误差反传神经网络(back propagation neural network,缩写为BPNN)。相对而言,BPNN具有非线性映射能力强、结构简单、泛化能力强、激活函数输入空间不受限且理论上可全局寻优等优点,因此,文章以它为基础,采用SAGFA改善其寻优速度和精度,以达到更好的预测效果。BPNN基本结构如图3所示。

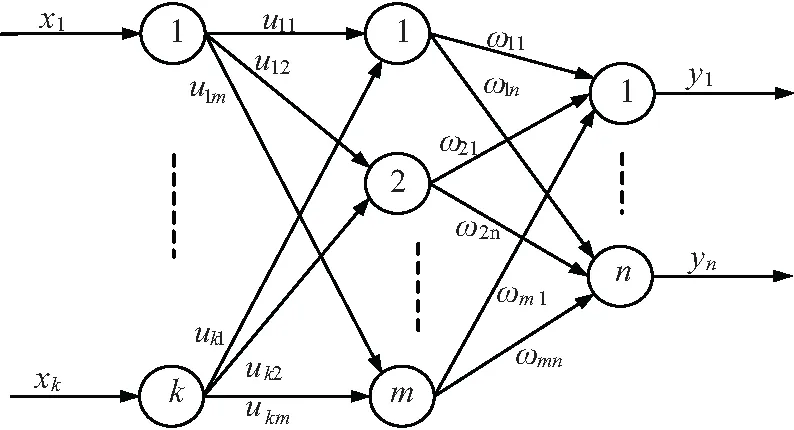
图3 BPNN原理框图

理论研究表明,所有非线性函数都可以采用单隐含层的前馈网络来映射,所以,文中的BPNN采用输入层、单隐含层和输出层的三层结构,每层由若干个节点(即神经元)组成,同层神经元之间无任何联系。其中网络节点的激活函数很重要,通常选用标准Sigmoid函数,可全局寻优。节点输出函数表达式为:

(8)

式中xi为神经元输入;y为神经元输出;θ为阈值;ωi为连接权值。

BPNN虽然具有上述优点,但也存在训练收敛有平缓区、高精度的训练完成时间较长的不足。训练的实质就是根据输入和输出的目标值,优化神经网络连接权值,使实际输出按照训练精度要求趋近目标值的过程,若能快速地找到全局最优的权值组合,就可一举克服上述不足。因此,文章采用SAGFA优化连接权值,提出SAGFA-BPNN网络。

SAGFA-BPNN采用SAGFA对BPNN参数进行优化,是将BPNN的各层间的连接权值进行编码,并按照一定的规则构成染色体,用与BPNN的辨识误差成反比例的适当函数作为适应度函数,利用SAGFA搜索到最优解。这些最优解的染色体编码,根据前述的规则解码,就得到了BP神经网络的最优化的各层间的连接权值。SAGFA-BPNN原理框图如图4所示。

从图4可以看出,SAGFA的染色体编码由BP神经网络的连接权值按照一定的顺序组成。图中给出的网络输入节点为k个,隐含层节点为m个,输出节点为n个,这样,染色体中的u11,…,ukm为输入层k个节点到隐含层的m个节点的连接权值,ω11,…,ωmn分别为隐含层m个节点到输出层n个节点的连接权值。

SAGFA的优化结果中染色体的不同位作为BP神经网络的不同支路的连接权值,由于SAGFA优化算法得到最优解,对应着适应度函数取得极大值,而对于BP神经网络则应该达到最小的辨识误差。因此,SAGFA算法的适应度函数为与辨识误差函数成反比例的函数,我们取适应度函数为:

g=1/(1+E)

(9)

式中g为适应度函数;E为BP神经网络训练的系统辨识误差。

2 基于PCA及SAGFA-BPNN的软件可靠性建模

2.1 实验数据的PCA处理

若实验数据维数太多,不仅会增加用于可靠性预测的神经网络的输入节点数,而且会增加样本噪声,影响预测的准确率,因此,维数太多时需要进行降维处理。

降维的方法较多[19],可以采取成分分析类的方法,如独立成分、主成分等,也可以采取回归分析类的方法,如逐步、多元、阶跃函数、样条及多项式等。由于主成分分析(PCA)可消除指标间的相关影响,且降维效果较好,所以,文中运用PCA进行数据处理,剔除影响模型准确率的冗余和干扰样本。

设原始数据矩阵为:

(10)

式中n为样本数,k为样本因数维数。

归一化后,将X的k个变量线性合成为m(k≥m)个新变量,如下:

(11)

1)yi与yj(i≠j;i,j=1,2,…,m)不相关;

2)y1为具有最大方差的线性组合;

3)y2满足第(1)条,亦为方差最大者;

4)y3～ym依此类推,依顺序确定。

新变量y1,y2,…,ym分别称为原变量中第1个、第2个、…、第m个主成分。第1个主成分y1的方差贡献率最大,依次递减。

文中建立可靠性模型时可适当选择前几个主成分,使方差的累积贡献率超过85%即可。

2.2 基于SAGFA-BPNN的软件可靠性建模

基于SAGFA-BPNN建立软件可靠性预测模型的主要步骤如下所示,流程图如图5所示。

以往模式中很难对业主的责任进行集中化划分，不能明确地指出。对于EPC工程的总承包模式来说，虽然一直是五方主体的责任不发生变化，总承包的企业还是需要承担总体责任，一旦工程涉及到勘测和设计与采购以及施工的问题，那么总承包就要承担一定的责任。在传统模式的基础上，设计施工的过程中会发生扯皮问题，EPC模式基础上的问题扯皮是在总承包的范围中出现的，必须要总承包进行内部把控以及管理，因此，对于总包管理制度和核心能力与人员专业提出较高的要求。如果不能很好地把控，所产生的风险就要由总包单位进行负责。此时，就需要分包和分包以及分包和主体施工之间协调管理有效地对接，一旦出现疏忽，势必会造成索赔。

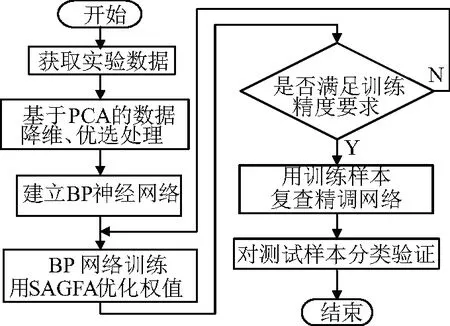
图5 建立软件可靠性预测模型的流程

1)进行软件测试,获得多维度的多次实验数据;

2)采用PCA降低维数、优化数据,减少神经网络输入节点数,以便于提高预测精度;

3)建立BP神经网络,确定输入、输出及隐含层的节点数;

4)输入训练样本数据,利用SAGFA优化BP神经网络的连接权值;

5)用训练样本数据复查精调神经网络完成全部网络训练。

将测试样本输入到训练好的SAGFA-BPNN进行分类预测,并输出结果。

3 采集终端软件可靠性预测建模实验

3.1 采集终端软件组成及可靠性分析

采集终端软件平台基于ARM平台和嵌入式操作系统,采用模块化设计,软件功能结构如图6所示。系统软件可以分为操作系统层和业务应用层,其中操作系统层就有约20项功能,业务应用层也有7项以上应用程序,还可以根据需要可以拓展软件功能。可见,采集终端软件系统是由很多个功能模块,或者说子系统组合而成,子系统间相互作用,相互协调完成系统功能。

图6 采集终端软件功能结构图

根据软件子系统的相对独立性,以及它们之间相互的调用情况可知,整个软件的系统故障率等于各子系统故障率与其调用系数乘积的累加[20],即:

(12)

式中πi为子系统Xi(i=1,2,…,n)的调用系数。

在可靠性预测实践中,πi值可采用子系统Xi的运行时间占整个系统运行时间的比例来表示。系统的可靠性函数为:

(13)

可见,系统的可靠性可以通过求解各个子系统的故障率来求得。

考虑到采集终端软件的复杂性,其可靠性分析可以通过软件的功能模块分解及可靠性建模来实现。

3.2 实验数据

采集终端基于ARM平台和嵌入式系统,由于嵌入式系统的独特性,其测试需要专用的测试工具,主流测试方法可分为静态分析法、动态测试法和综合测试法三类。采用可靠性增长测试阶段的综合性测试法所获得的部分数据进行研究。为节省篇幅,数据采用图7的曲线呈现。

图7 实验数据曲线

3.3 软件可靠性预测建模实验结果与分析

基于前面的研究结果,采用PCA降维、去噪,得到的主成分输入到SAGFA-BPNN中进行可靠性预测建模的实验方法。

建模实验采用MATLAB仿真软件进行。为了观察PCA的效果,以及主成分贡献率对预测结果的影响,文章选择不同的保留率进行仿真实验。

SAGFA-BPNN的训练精度如果设置的太高则可能造成过训练,降低泛化能力,设置的太低则影响预测的准确率,因此,为了兼顾泛化能力和预测准确率,训练的均方误差设置为1%。

预测目标值Rti依据式(13)计算得到,神经网络的输出为预测值Ri,则预测的绝对误差为:

δi=|Ri-Rti|

(14)

式中δi为第i个样本的预测绝对误差;Rti为第i组数据的目标值;Ri为第i组数据的预测值。

实验采用18组样本作为训练样本,另外的9组样本作为检验样本。不同贡献率的软件可靠性预测结果如图8所示,预测的绝对误差如图9所示。可以看出:第一,对每组数据都能较准确地预测出可靠性;第二,模拟保留率为90%的曲线与保留率100%的曲线相比,前者的模拟效果略微好于后者,这说明采用PCA进行数据预处理,不仅可以降低维度,还可以在一定程度上去除冗余信息及减小噪声干扰,更有利于预测,噪声信息越多,这种现象越明显;第三,从误差的曲线来看,所有点的绝对误差都在0.07以内,平均误差更低,这是由于训练的均方误差设置为1%的结果,若有需要,可通过提高训练指标以减小绝对误差;第四,所建立的软件可靠性模型具有很强的泛化能力,对检验样本的识别准确性也非常好。实验证明,文中提出的可靠性建模方法可行,完全满足软件可靠性预测建模的要求。

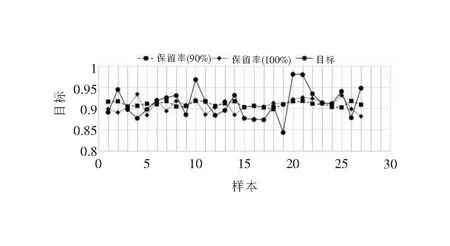
图8 不同贡献率的软件可靠性预测结果

图9 不同贡献率的预测误差曲线

4 结束语

针对软件可靠性预测问题,在创建优化算法并提出SAGFA-BPNN的基础上,进一步提出了基于PCA和SAGFA-BPNN的软件可靠性预测模型建模方法,并成功应用于采集终端软件可靠性预测建模。该方法克服了以往的基于多种神经网络的软件可靠性建模存在的收敛速度慢、针对存在冗余和噪声数据的情况预测准确率低的难题。仿真及实验结果表明,SAGFA-BPNN训练收敛快、全局寻优能力强,所建立的软件可靠性模型具有很强的泛化能力,训练速度及预测效果优于典型神经网络的预测模型。文章方法具有重要的参考价值。