基于复合吸附剂的固定除湿床传递特性的数值模拟

肖 鑫，韩郑良，王一凡

(东华大学 a.环境科学与工程学院,b.空气环境与建筑节能研究所, 上海 201620)

湿度是影响人体热舒适感的重要环境因素,也是评价环境舒适度的重要指标。有效控制环境湿度对于改善居住条件、发展生产技术等具有重要意义[1]。目前人们主要依靠空调的冷却除湿模式控制环境湿度,该方式存在再热再湿、热湿比难适应和空气品质恶化等问题,给环境带来很大的压力[2]。固体吸附除湿以低品位热能为驱动能源,具有空气处理量大以及节能的优点,因此成为除湿的一个主流研究方向[3-4]。

在固定床的除湿过程中,除湿床的结构对除湿效果有重要影响。为优化除湿床的结构,提高除湿效果,研究者们通过数值模拟法探究了单料填充床除湿过程中的各种影响因素。Sun等[5]研究发现,在相同测试条件和相同颗粒床体积条件下,比表面积较大、粒径较小的颗粒能够吸附更多的水分,释放更多的热量。Rady等[6]采用有限体积法模拟了硅胶填充床的除湿过程,发现引入封装相变材料(EPCM)可降低吸附产生的热量,并且EPCM的相变温度越低,系统除湿效率越高。Ramzy等[7]采用修正的固体侧阻模型模拟了硅胶填充床的除湿过程,发现在相同的干燥剂用量和空气质量流量条件下,复合颗粒的厚度比从1.0降至0.2时,固定床的压降约降低60%,吸附效率提高15.5%。Smejkal等[8]研究发现,湿空气与沸石干燥剂接触时,两者之间的温差较大;当吸附速率达到最大值时,在固定床边界附近有最大温差(约为2 K),该值由狄利克雷边界条件引起,而在其他位置,温差最大值约为0.7 K。唐开[9]研究发现,在低湿度工况下,再生温度高于60 ℃时,13X型分子筛除湿床单位时间内单位质量干燥剂的除湿量高于改性硅胶除湿床。姚小龙[10]研究发现,轴向扩散系数的变化对吸附柱的传质影响有限;吸附柱高度的增加和气体流速的减少会延长水蒸气穿透时间,但并不影响水蒸气在吸附柱中的扩散规律。吕宁[11]研究发现,入口空气温湿度的增加会导致除湿效率的降低,而再生空气流速和再生温度的提高对除湿床的再生效果影响较小。许梦玫[12]研究发现,随着再生空气温度的升高,除湿量、除湿效率、再生度均有所增大,但除湿性能系数有所下降。

研究者们也基于双料填充床对除湿过程进行了数值模拟研究。Yu等[13]分析了循环时间、固定床的尺寸和吸附-解吸速率常数等参数对固定床除湿性能的影响,结果显示可以通过结合水加热和冷却装置来提高的固定床除湿性能;采用水冷方式时,固体干燥剂的水蒸气吸附能力有所增加。刘科验等[14]研究发现,Al掺杂硅胶与NW-162两种新型吸附材料的应用可使除湿系统的吸湿速率提高20%,持续工作时间增加40%。Awad等[15]模拟了硅胶填充床的除湿过程,发现固定床直径比的增大可提高床层内的压降,增强床层在短时间内的吸附能力。Ramzy等[16]基于实验除湿系统和理论分析,提出增加除湿床的长度可降低出口空气的湿度比,提高出口空气温度,增加循环时间,减少控制系统的负荷,从而提高变温吸附循环效率。

上述模拟研究的不足之处在于没有对除湿过程中的影响因素进行完整分析,并且未系统分析多因素耦合作用对除湿过程的影响。本文从入口空气相对湿度(RH)、入口空气流速、入口空气温度、固定床结构尺寸4个方面系统地研究除湿过程中的影响因素。基于质量守恒方程、动量守恒方程、连续性方程和Langmuir吸附等温模型,建立海藻酸钠/硅藻土固定除湿床的数值模型,探究入口空气相对湿度、入口空气流速、入口空气温度、固定床结构尺寸对除湿效果的影响。

1 数学模型

采用COMSOL Multiphysics 5.6软件模拟固定床的除湿过程。通过将Brinkman方程、多孔介质稀物质传递两个物理场接口相互耦合,建立数值模拟模型,该模型基于以下假设[10,17-18]建立:1)气体符合理想气体定律,视为不可压缩流体,忽略其惯性作用;2)多孔介质是均匀的,吸附瞬间达到平衡;3)吸附剂的物理性质恒定;4)固定床的初始温度和压力是均匀的;5)忽略传热对吸附产生的影响;6)忽略气体速度、气体浓度沿固定床径向的梯度变化。

1.1 几何构建

由于气体速度、浓度沿固定床径向的梯度变化可以忽略,因此吸附柱每个截面的吸附情况基本一致。为简化模型,构建固定床的二维平面模型,如图1所示。

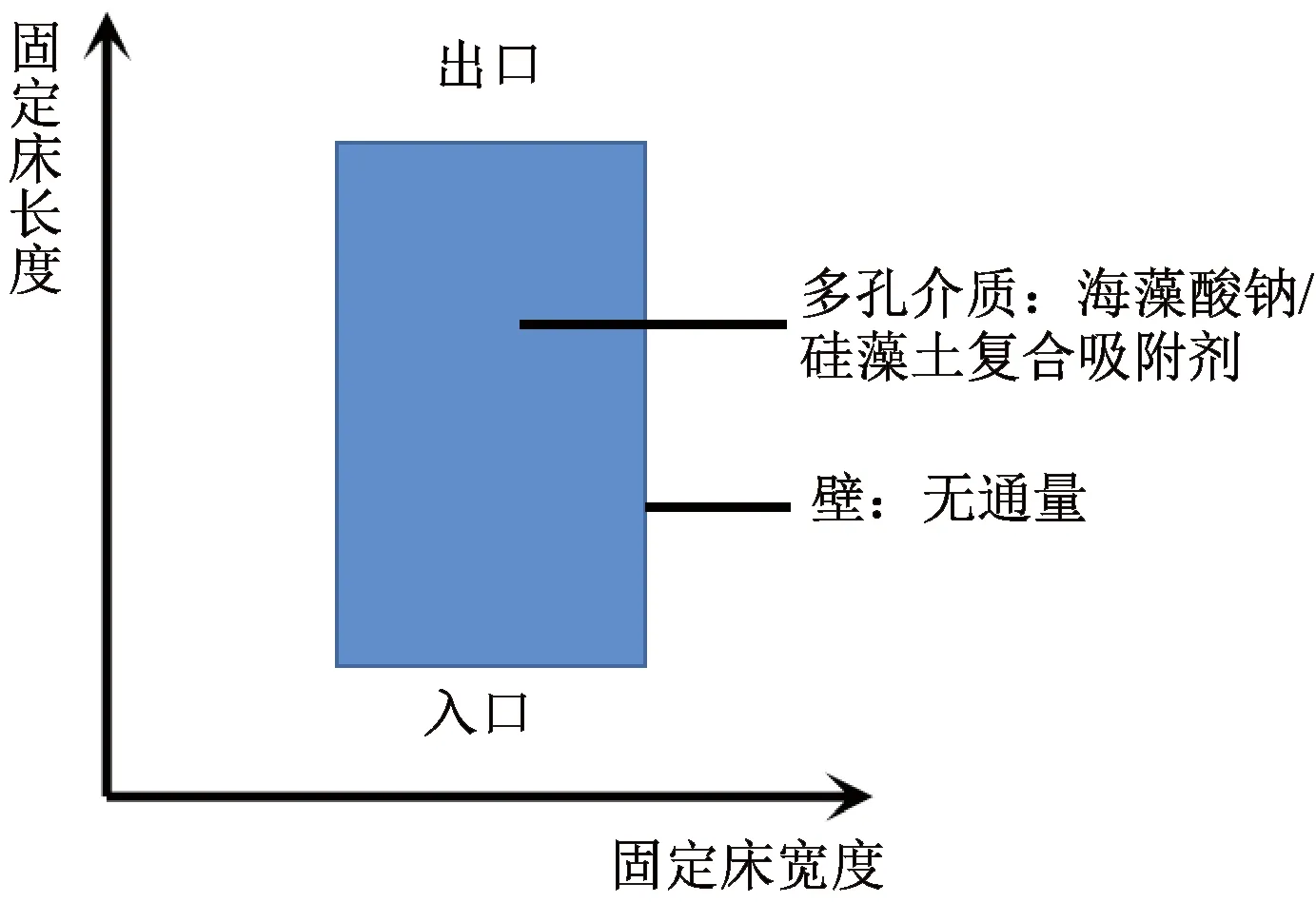
图1 二维固定床平面模型示意图Fig.1 Schematic diagram of the model of two-dimensional fixed bed

1.2 物理场选择

1.2.1 Brinkman方程

Brinkman方程接口模拟气体速度变化,主要包括连续性方程和动量守恒方程。连续性方程和动量方程分别如式(1)和式(2)所示。

(1)

(2)

式中:ρ为气体密度,kg/m3;εp为孔隙率;u为气体流速,m/s;t为时间,s;p为压力,Pa;μ为气体动力粘度,Pa/s;T为热力学温度,K;K为渗透率,m2;Qbr为质量源,kg/(m3·s);I为单位张量;F为力项,kg/(m2·s2)。

其中,多孔介质的渗透率由Kozeny Carmon方程[19]计算:

(3)

式中:Dav为孔隙平均直径,m。

湿空气的密度随着相对湿度的变化而变化,其表达式为

(4)

式中:pa为空气绝对压力,Pa;pb为饱和水蒸气压力,Pa;n为相对湿度。

1.2.2 多孔介质稀物质传递

多孔介质稀物质传递接口模拟气体浓度变化,主要包括质量守恒方程,其表达式为

(5)

式中:ci为水蒸气浓度,mol/m3;Df为分子扩散系数,m2/s;Ri为反应速率,mol/(m3·s)。

有效扩散系数Dc的表达式为

Dc=εpτDf

(6)

式中:Dc为气体有效扩散系数,m2/s;τ为曲折度。

采用Millington-Quirk模型[20]计算曲折度τ,表达式为

(7)

采用Langmuir吸附等温模型模拟吸附平衡状态,该模型表达式为

(8)

式中:qe为平衡吸附量,g/g;qm为理论饱和吸附量,g/g;ρe为吸附平衡质量浓度,g/L;KL为吸附平衡常数,L/g。

平衡吸附量表达式为

(9)

式中:V为气体体积,m3;ρ0为吸附质初始质量浓度,g/L;m为吸附剂质量,g。

1.3 材料属性

本研究中,气体为不同湿度的湿空气,固体为海藻酸钠/硅藻土复合吸附剂。不同入口空气相对湿度下固体、气体的物性参数如表1和表2所示。

表1 固体与气体的物性参数[17, 21]Table 1 Physical parameters of solid and gas[17, 21]

表2 不同相对湿度下气体的密度Table 2 Densities of gas under different relative humidity

1.4 模拟参数设计

采用控制变量法探究入口空气相对湿度、入口空气流速、入口空气温度、固定除湿床的结构尺寸对除湿效果的影响。入口空气相对湿度设置为40%、50%、60%、70%、80%,入口空气流速设置为0.05、0.10、0.15、0.20、0.25 m/s,入口空气温度设置为15、20、25、30 ℃,二维模型中固定床的面积设置为450、600 mm2,设置6组长宽比,分别为45∶10(即9∶2)、30:15(即2∶1)、60∶10(即6∶1)、50∶12(即25∶6)、40∶15(即8∶3)、30∶20(即3∶2)。

1.5 模型验证与网格独立性分析

1.5.1 模型验证

为了确保二维模型的准确性,引用张艺馨[17]的研究数据进行验证。采用基于有限元分析的固定床吸附模型计算入口Pb2+质量浓度为20 mg/L,入口流速为12 m/h,床层高度为60 cm时多孔介质的吸附效果,具体结果如图2(a)所示。由图2(a)可知,本模型的计算结果与原文献结果基本一致,验证了本模型的准确性。采用三维模型进行对比计算以进一步验证二维模型的准确性。选用入口空气相对湿度为60%,入口空气流速为0.10 m/s,入口空气温度为25 ℃,固定床面积为450 mm2,长宽比为2∶1作为二维模型条件;入口空气相对湿度为60%,入口空气流速为0.10 m/s,入口空气温度为25 ℃,体积为2 250 mm3,长宽高比为6∶3∶1作为三维模型条件。二维模型与三维模型的计算结果如图2(b)所示。由其可以看出,二维模型与三维模型的计算结果基本一致,故本文采用二维模型进行分析。

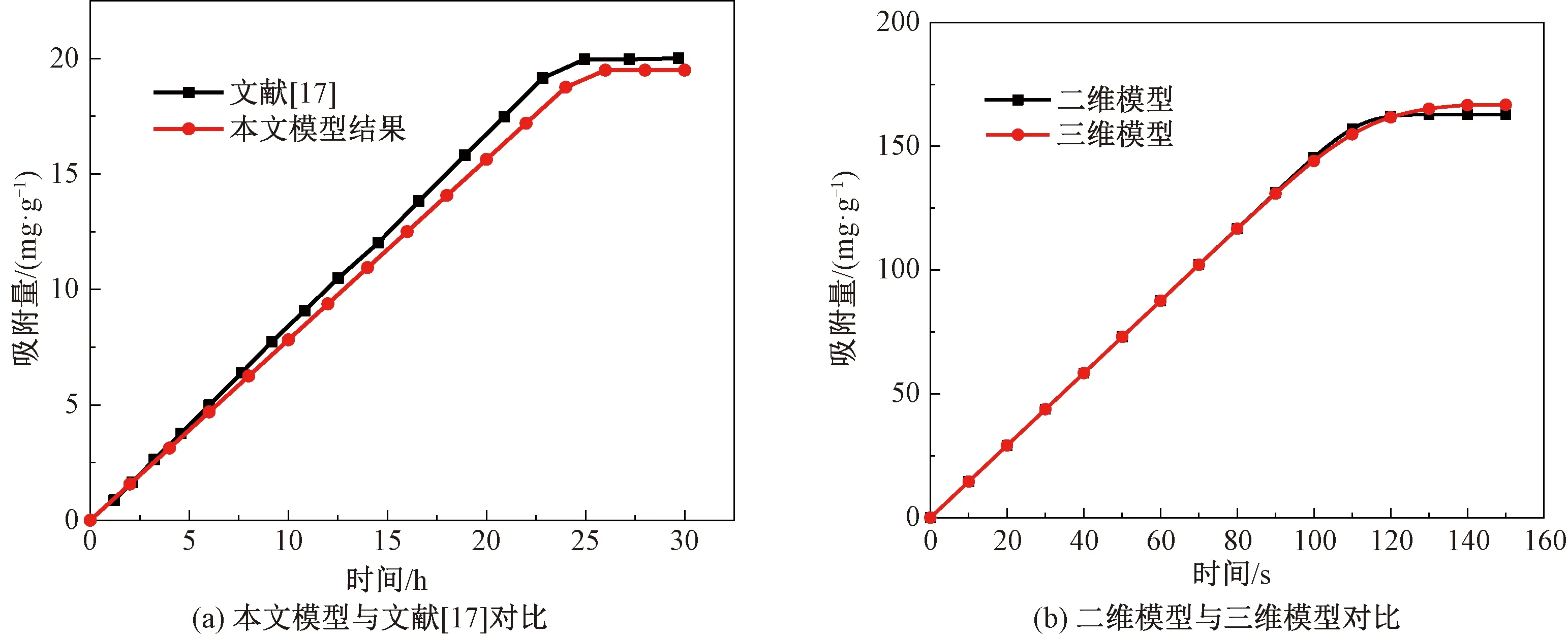
图2 二维模型验证Fig.2 Validation of the 2D model

1.5.2 网格独立性分析

为分析网格独立性,在入口空气相对湿度为60%,入口空气流速为0.10 m/s,入口空气温度为25 ℃,固定床面积为450 mm2,长宽比为2∶1的条件下,对比超细化、常规、超粗化三种网格尺寸(网格数分别为9 304、1 414、294)下的计算结果如图3所示。结合图3,考虑到计算时间,本文选用常规尺寸网格(网格数为1 414)进行计算。

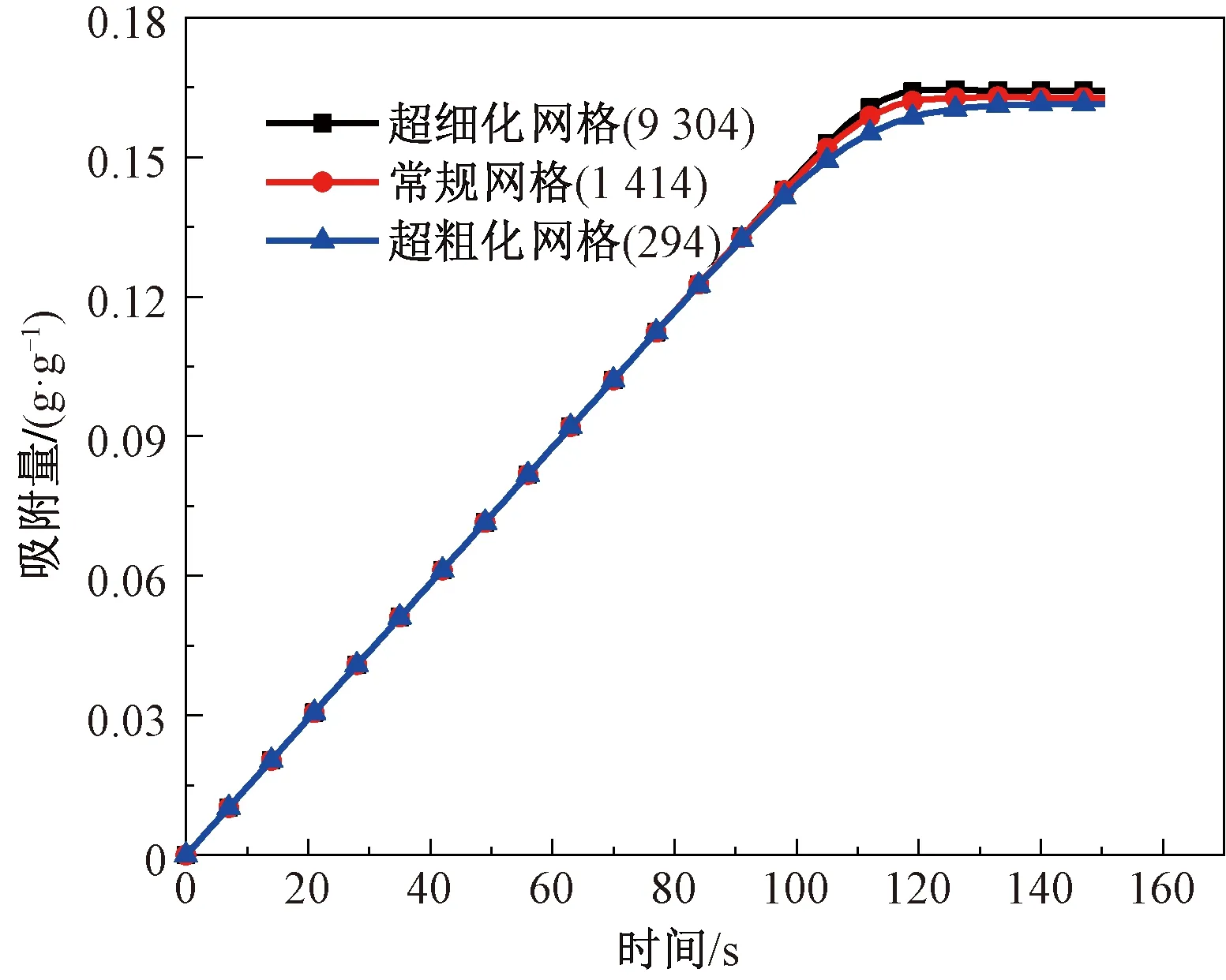
图3 网格独立性分析Fig.3 Analysis of grid independence

2 结果与分析

2.1 不同入口空气相对湿度的数值模拟对比

固定床入口空气相对湿度分别为40%、50%、60%、70%、80%,入口空气流速为0.10 m/s,入口空气温度为25 ℃,面积为450 mm2,长宽比为2∶1。图4和图5为不同入口空气相对湿度下固定床的水蒸气浓度云图(吸附时间t=100 s)和吸附动力学曲线。由图4和图5可知:同一时刻不同入口空气相对湿度情况下气体所处位置基本一致;改变入口空气的相对湿度,对穿透时间和达到吸附平衡的时间影响很小,而对平衡吸附量的影响较大。随着入口空气相对湿度的增大,平衡吸附量增大,当入口空气相对湿度为80%时,平衡吸附量最大(0.215 g/g)。这是由于在相同送风条件下,入口空气相对湿度越大,水蒸气的分压力越大,传质过程得到强化,从而增强了吸附效果。此外,入口空气相对湿度越大,同一时刻出口空气湿度及其增长率越大。这表明随着吸附剂吸附量的增大,入口空气相对湿度越高,固定床吸附效果越差;在吸附剂达到吸附平衡前,入口空气相对湿度越大时,出口空气湿度的增速越快,吸附效果越差。故增加入口空气的相对湿度有助于提高吸附量,但相对湿度过高会影响固定床的除湿效率,甚至对吸附效果产生抑制作用[12]。因此,入口空气相对湿度并不是越高越好,合适的相对湿度才能使吸附剂的吸附效果趋于最大化。

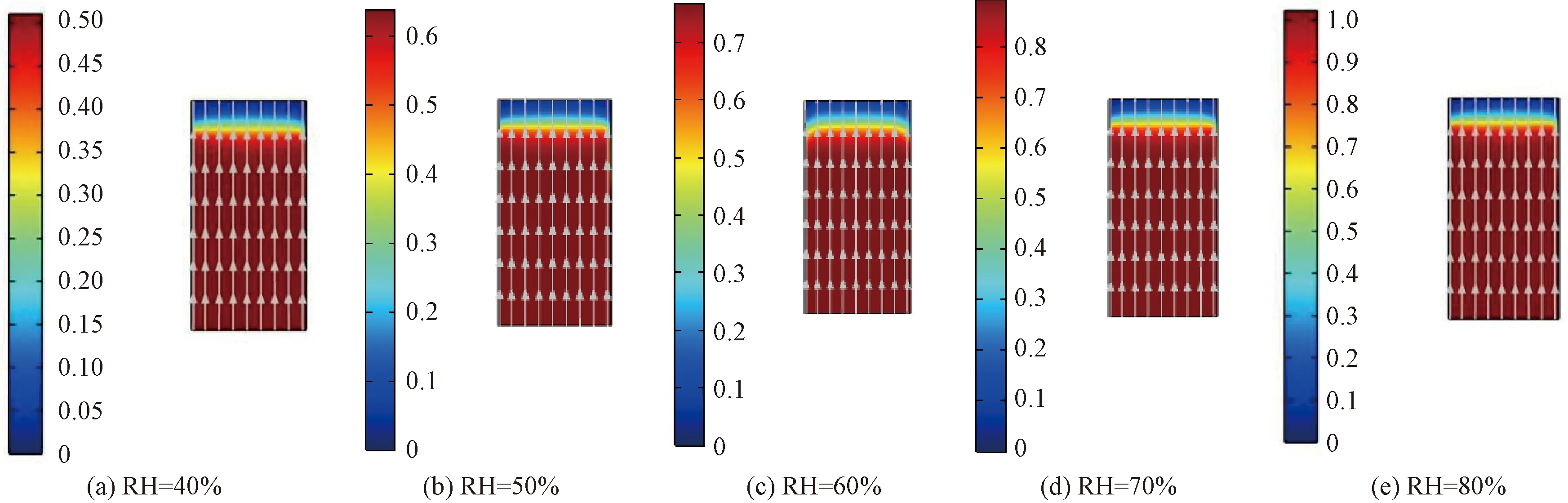
图4 不同入口空气相对湿度下固定床的浓度云图(t=100 s)Fig.4 Concentration contour of fixed bed under different relative humidity of inlet air(t=100 s)

图5 不同入口空气相对湿度下固定床的吸附动力学曲线Fig.5 Adsorption kinetics curves of fixed bed under different relative humidity of inlet air

2.2 不同入口空气流速的数值模拟对比

固定床的入口空气流速分别为0.05、0.10、0.15、0.20、0.25 m/s,入口空气相对湿度为60%,入口空气温度为25 ℃,面积为450 mm2,长宽比为2∶1。图6和图7为不同入口空气相对湿度下固定床的浓度云图和吸附动力学曲线。由图6和图7可知,入口空气流速越大,气体传递至固定床相同位置所需时间越短,穿透时间和达到吸附平衡所需的时间越少,平衡吸附量越小,吸附效果越差,如入口空气流速为0.25 m/s时,平衡吸附量仅为0.065 g/g。这是因为入口空气流速的增加,空气与吸附剂表面的接触时间变短,接触不充分,从而吸附剂的吸附效果降低。此外,入口空气流速越高,同一时刻出口空气湿度及其增长率越大。这表明随着吸附剂吸附量的增大,入口空气流速高的吸附效果逐渐变差;在吸附剂达到吸附平衡前,入口空气流速越大,出口空气湿度的增速越快,吸附效果越差。因此增加入口空气流速会削弱吸附剂的吸附效果。

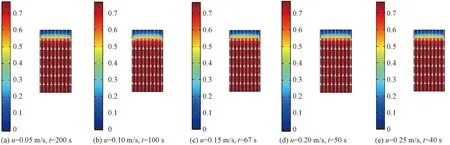
图6 不同入口空气流速下固定床的浓度云图Fig.6 Concentration contour of fixed bed under different velocities of inlet air

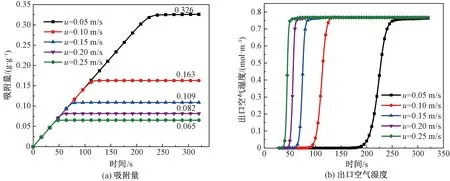
图7 不同入口空气流速下固定床的吸附动力学曲线Fig.7 Adsorption kinetics curves of fixed bed under different velocities of inlet air

2.3 不同固定床结构尺寸的数值模拟对比

第一组固定床的面积为450 mm2,两组长宽比分别为9∶2、2∶1,入口空气相对湿度为60%,入口空气流速为0.10 m/s,入口空气温度为25 ℃。第二组固定床的面积为600 mm2,4组长宽比分别为6∶1、25∶6、8∶3、3∶2,入口空气相对湿度为60%,入口空气流速为0.10 m/s,入口空气温度为25 ℃。

图8和图9为不同结构尺寸下固定床的浓度云图和吸附动力学曲线,其中a∶b表示长宽比。由图8和图9可知,固定床长宽比越大,同一时刻气体所处位置距固定床出口越远,穿透时间和达到吸附平衡所需时间越长,平衡吸附量越大,吸附效果越好,如在固定床面积为600 mm2、长宽比为6∶1时,平衡吸附量可达0.329 g/g,高于其他尺寸固定床的平衡吸附量。这是由于在一定送风条件下,固体除湿床的长度决定了空气在吸附床内的流动时间,固定床的长宽比越大,空气流动时间越长,与吸附剂表面接触越充分,吸附效果越强。此外,固定床的长宽比越大,同一时刻出口空气湿度及其增长率越小。这表明随着吸附剂吸附量的增大,固定床的长宽比越大,吸附剂的吸附效果越强;在吸附剂将要达到吸附平衡时,固定床的长宽比越大,出口空气湿度的增速越慢,吸附效果越强。

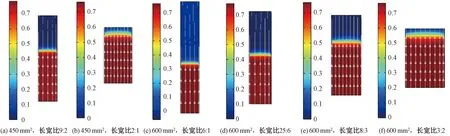
图8 不同结构尺寸下固定床的浓度云图(t=100 s)Fig.8 Concentration contour of fixed bed under different structures(t=100 s)

因此,固定床的长宽比的增加对吸附剂的吸附效果有积极影响,但这与边界条件的设置有关。固定床的长度以及入口空气的流速共同决定了气体在固定床中的流动时间。此外,在增大固定床的长宽比时应考虑固定床整体结构的合理性,以及压降的影响。

2.4 不同入口空气温度的模拟对比

固定床的入口空气温度分别为15、20、25、30 ℃,入口空气相对湿度为60%,入口空气流速为0.10 m/s,面积为450 mm2,长宽比为2∶1。

25 ℃时固定床的浓度云图见图4(c),其他温度下同一时刻固定床的浓度云图与其基本一致。图10为不同温度下固定床的吸附动力学曲线。由图10可知,入口空气温度对本研究条件下的吸附效果影响很小,可以忽略不计。这主要是由2个原因所致:1)模拟忽略了入口空气与吸附剂之间的对流换热与热传导,以及吸附过程中产生的吸附热,即模拟为单一传质过程。2)入口温度的变化会影响湿空气的密度和动力黏度,当温度从15 ℃增至30 ℃时,湿空气密度从1.220 4 kg/m3增至1.153 5 kg/m3,动力黏度从1.79×10-5Pa/s增至1.86×10-5Pa/s,密度和动力黏度变化很小,反映到吸附动力学曲线上时,平衡吸附量变化极其微小。综合上述两个原因,在单一传质过程中,入口空气温度的变化对吸附效果的影响可以忽略不计。

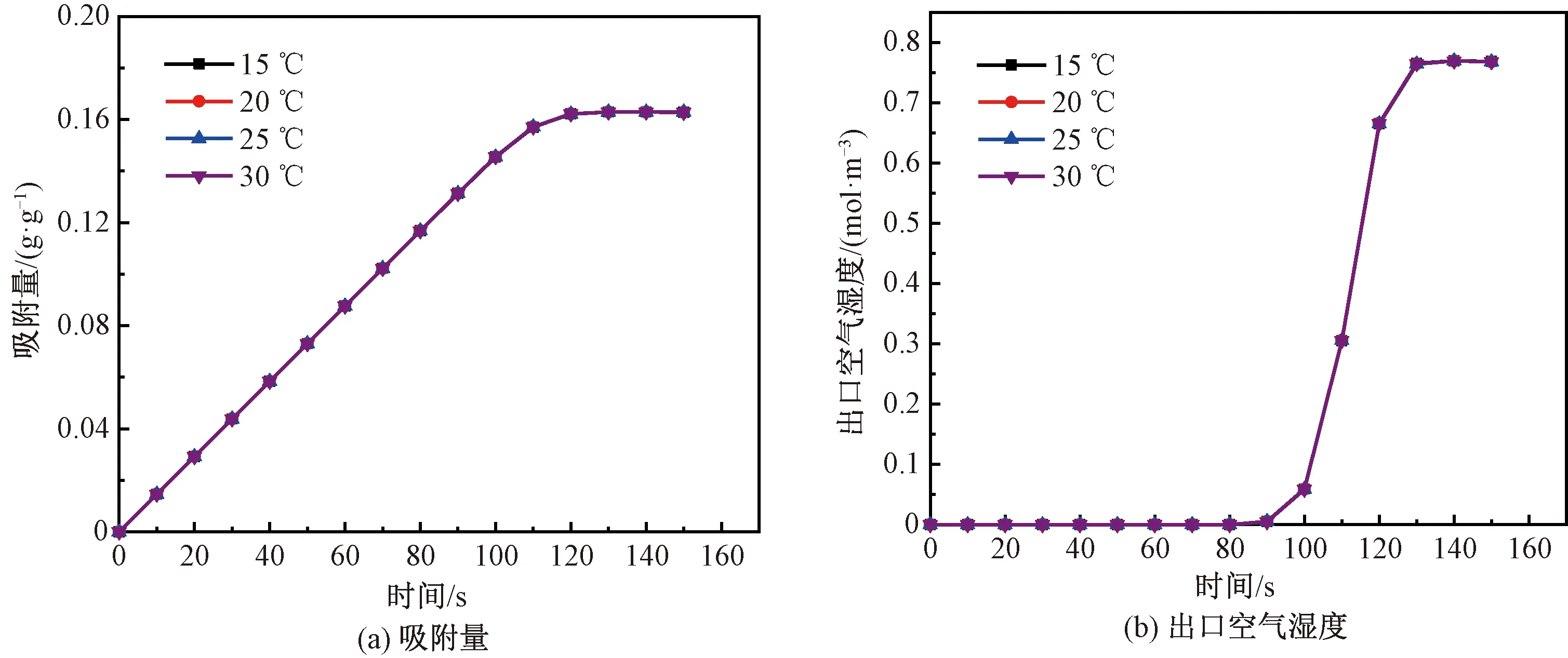
图10 不同温度下固定床的吸附动力学曲线Fig.10 Adsorption kinetics curves of fixed bed at different temperatures

3 结 论

对海藻酸钠/硅藻土固定除湿床的除湿过程进行数值模拟,通过改变边界条件,探究不同因素对吸附效果的影响。结果表明:在单一传质条件下,入口空气相对湿度、入口空气流速、固定床表面长宽比的变化对吸附剂的吸附效果有不同的影响,而入口空气温度的变化对吸附效果的影响可以忽略。具体如下:

1)增大入口空气相对湿度可以提高平衡吸附量。在入口空气相对湿度为80%、流速为0.10 m/s、温度为25 ℃,固定床面积为450 mm2、长宽比为2∶1的条件下,平衡吸附量可达0.215 g/g,高于其他较低相对湿度条件下的平衡吸附量。但是过高的相对湿度不利于吸附剂长期稳定的使用,会对吸附效果产生抑制作用。

2)入口空气流速与吸附效果成负相关。在入口空气流速为0.25 m/s、相对湿度为60%、温度为25 ℃,固定床面积为450 mm2、长宽比为2∶1的条件下,平衡吸附量为0.065 g/g,低于其他较低流速条件下的平衡吸附量。

3)固定床二维表面的长宽比对吸附效果的影响取决于边界条件的设置。固定除湿床越长,即长宽比越大,吸附效果越强。在固定床的面积为600 mm2、长宽比为6∶1,入口空气相对湿度为60%、流速为0.10 m/s、温度为25 ℃的条件下,平衡吸附量为0.329 g/g,高于其他较低固定床长度条件下的平衡吸附量。但增加长宽比时应考虑固定床整体结构的合理性以及压降的影响。