基于响应曲面分析的纬编3D凹孔针织物保暖性能研究

王建萍，王 莉，姚晓凤，1b，沈德垚，1b，刘 莉

(1.东华大学 a.服装与艺术设计学院,b.现代服装设计与技术教育部重点实验室,c.上海市纺织智能制造与工程一带一路国际联合实验室, 上海 200051;2.同济大学 上海国际设计创新研究院, 上海 200092;3.北京服装学院 服装艺术与工程学院, 北京 100029)

随着针织行业的飞速发展,各种针织服装产品越来越丰富,尤其是秋冬季的服装中,针织类目占比不断增加。由于冬季低温环境的特点,保暖性成为冬季面料开发的一项重要内容[1-3],针织面料的空气层能通过贮存一定的空气量来增加织物的保暖性,因此针织面料成为冬装面料的重要组成部分[4-5]。针织产品织造过程中的移圈、抽针等工艺技术能使织造出表面产生明显凸起或凹孔肌理的凹凸结构针织物[6-7],使其具有较好的保暖效果。在无缝针织面料织造中,使用无缝针织纬编圆机二功位可实现成圈与浮线,通过设计吊针组织和平针组织的组合可以织造出一定3D凹孔效果的结构,但目前这种结构常用于无缝内衣胸部的收胸组织(提胸组织)中[8-10]。研究[11]指出,设计一个组织循环内不同吊针路数与平针结构交替组合后在织物的表面会形成非闭合立体凹孔,随着吊针路数的增多凹孔越深3D效果越明显,通过扩散组织循环数量,单个3D凹孔在织物面层上连续均匀间隔排列,而在织物里层,其相互连通形成一条条中空凹陷通道,与人体皮肤间隔接触,可增加织物的保暖性。因此,吊针组织与平针组织构成的3D凹孔效果织物保暖性较好,两种组织参数的变化会改变织物的立体形态效果进而会影响织物的保暖性,但具体的影响关系缺少相关研究,组织参数的变化对于3D凹孔结构针织物保暖性能的影响也没有进一步探讨,目前相关成果难以指导实际生产实践。本文为探究组织结构设计参数对纬编3D凹孔针织物保暖性能的影响,采用双股70 dtex DRYARN®纱线作面纱,50 dtex DRYARN®纱线包覆17 dtex氨纶作底纱,设计织造一个组织循环内不同吊针路数、连续成圈针数及平针路数的纬编3D凹孔针织物,并对选取的15种织物试样的保暖性能相关指标进行测试与分析,得出组织循环内吊针路数、连续成圈针数及平针路数对3D凹孔针织物保暖性能的影响关系,为开发保暖性能优良的3D凹孔针织物提供了高效的工艺参数方案。

1 试验设计

1.1 单因素试验设计

基于一个组织循环内吊针路数、连续成圈针数、平针路数3个因素,运用控制变量法织造15种试样进行试验。将试样分为3组进行单因素试验,选择一个因素参数作为变量,控制剩余2因素不变,将吊针路数作为变量因素组时为a组,连续成圈针数作为变量因素组记为b组, 平针路数作为变量因素记为c组,根据市场调研和实际生产经验选取每个参数的5个水平见表1。

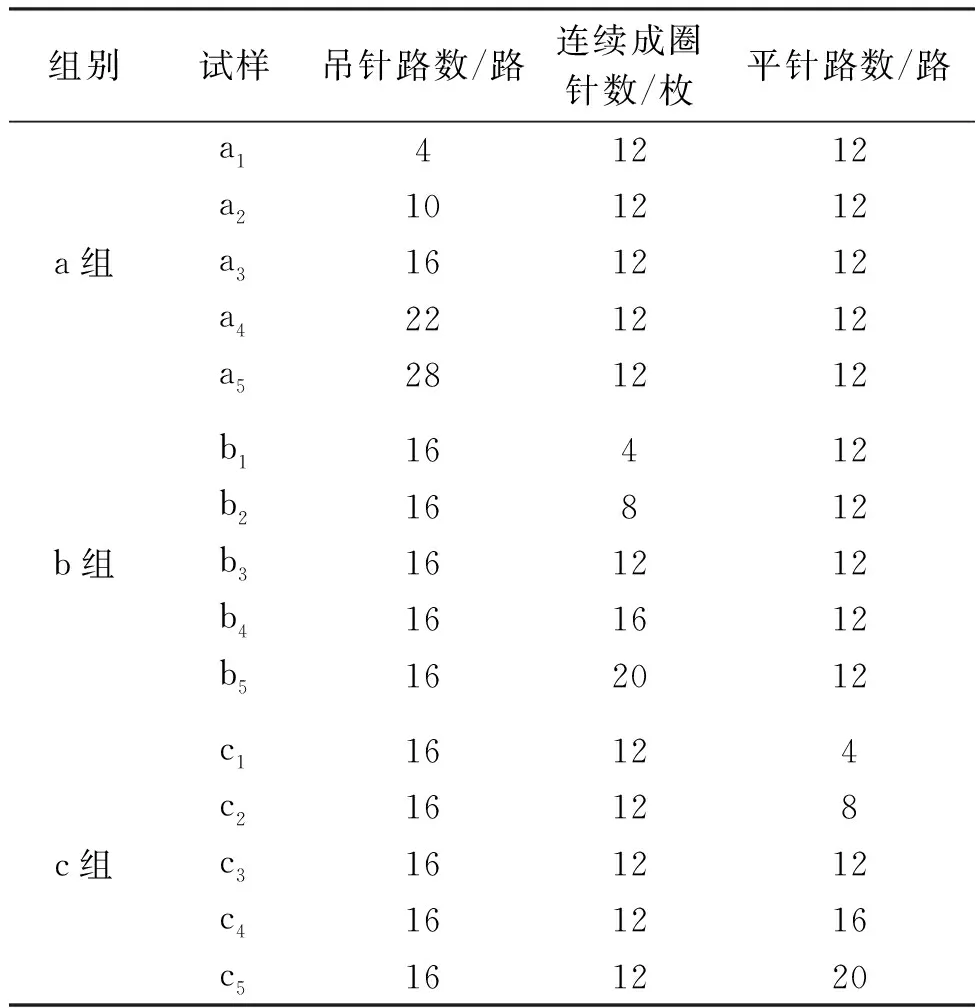
表1 单因素试验设计方案Table 1 Single factor experimental design scheme

1.2 多因素试验设计

响应曲面分析是一种综合试验设计和数学建模的优化方法,研究两个或多个因素之间的交互作用,并全面研究在最短时间内对所选试验参数[12],且具有成本低、试验次数少等优点。本文根据单因素试验分析结果,选取3因素3水平采用Design Expert8.0软件进行正交试验设计做Box-Behnken 试验方案,以研究吊针路数、连续成圈针数、平针路数等3因素对织物性能的影响关系。试验自变量吊针路数、连续成圈针数、平针路数及其水平如表2所示,其中0为中间值,-1为低值,1为高值。

表2 试验自变量及其水平表Table 2 Test independent variables and level tables

2 试验方法

2.1 织物织造仪器

采用SANTONI TOP2型八路单面电子提花针织圆机。提花针织圆机的成圈系统为8 F,针距0.907 mm(28E),针数为1248针,筒径为356 mm。

2.2 织物编织意匠图

凹孔针织物编织意匠图如图1所示。由图1可知,凹孔织物在为吊针路数为16路,连续成圈针数为10枚,平针路数为10路的一个组织循环下编织。

图1 凹孔针织物编织意匠图Fig.1 Knitting artisan of 3D concave welf-knitted fabric

2.3 织物参数测试方法

在温度为(20±2)℃,相对湿度为(65±2)%的环境下,采用 YG141N 型数字式织物厚度仪(参照GB/T 3820—1997《纺织品和纺织制品厚度的测定》)对15种织物试样进行厚度的测试,每种织物测试5次,取平均值。参照GB/T 11048—2008《纺织品 生理舒适性 稳态条件下热阻和温阻的测定》,采用YG606E型纺织品热阻测量仪对织物的保暖性能进行测试,热板温度为35 ℃,分别剪取每种织物规格为35 cm×35 cm的试样3块进行测试,结果取平均值。

3 试验结果与分析

3.1 单因素试验结果与分析

分别测试根据表1试验方案设计的15种3D凹孔针织物的厚度和克罗值,测试结果如表3所示。由表3和表1可知,在连续成圈针数为12枚,平针路数为12路不变的情况下,改变吊针路数值的5种试样(a1～a5),其中,试样a1厚度与克罗值最小,分别为1.386 mm、 0.466 clo;试样a5的厚度和克罗值最大,分别为4.322 mm、0.803 clo。

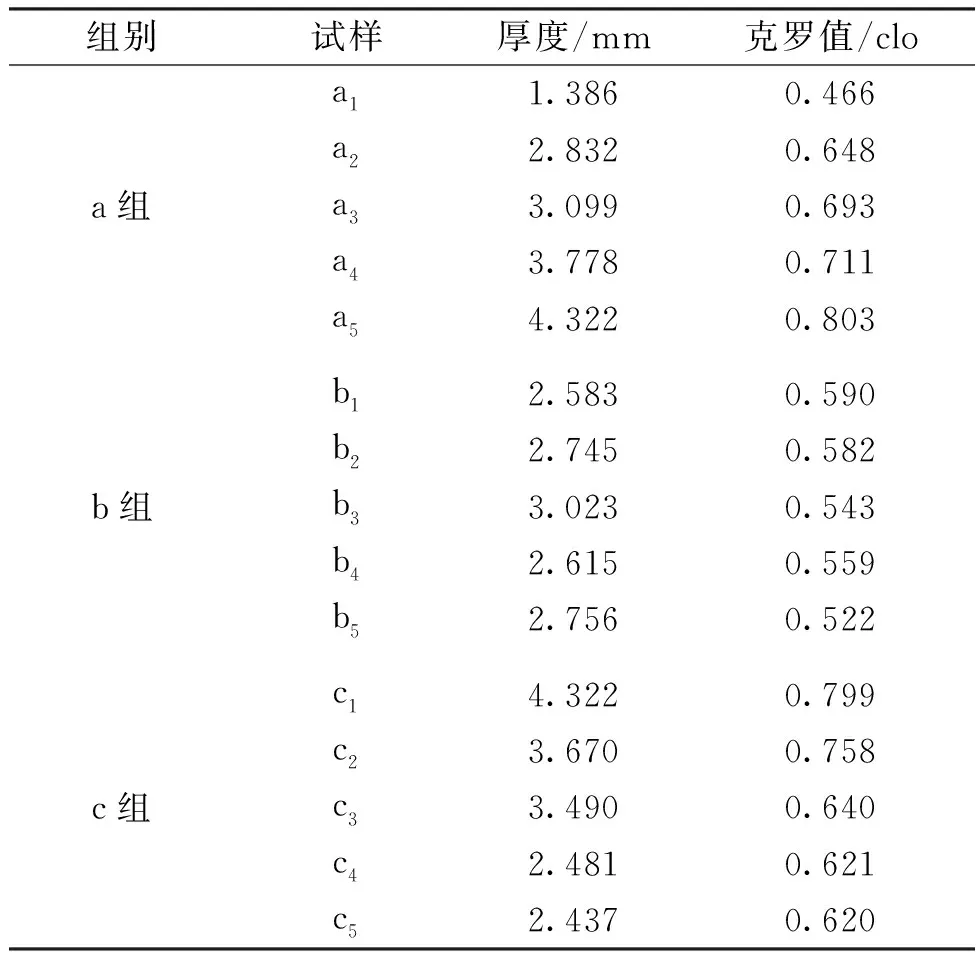
表3 单因素试验测试结果Table 3 Single factor test results

在吊针路数为为16路,平针路数为12路不变的情况下,改变连续成圈针数值的5种试样(b1～b5),试样b3厚度最大,为3.032 mm;试样b1厚度最小,为2.583 mm。此外,试样b1的克罗值最大,为0.590 clo, 试样b5的克罗值最小,为0.522 clo。

在吊针路数为16路,连续成圈针数为12枚不变的情况下,改变平针路数值的5种试样(c1～c5),试样c1的厚度和克罗值最大,分别为4.322 mm、0.799 clo;试样c5的厚度和克罗值最小,分别为2.437 mm、0.619 clo。

吊针路数值对织物指标的影响结果如图2所示。由图2可知,在连续成圈针数为6枚、平针路数为12路的情况下,只改变1个组织循环内吊针路数就可以改变织物3D凹孔的孔洞深度,随着吊针路数的增加,织物厚度与克罗值逐渐增加。这是由于吊针路数增加使得3D凹孔孔洞逐渐变深会使织物厚度变大,同时使凹孔空间变大可承托更多静止空气,两者共同作用使得织物克罗值增加,保暖性增强。

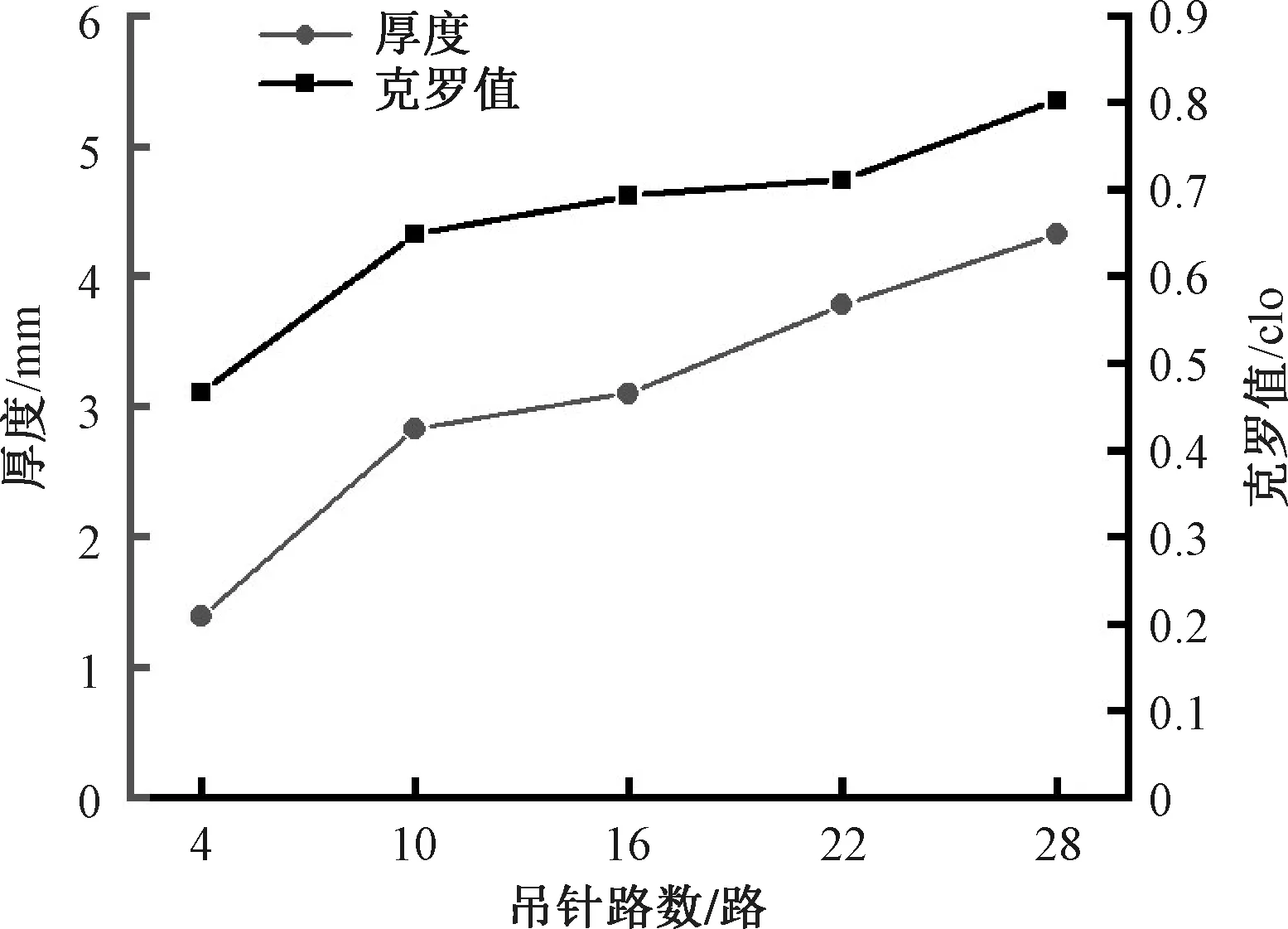
图2 吊针路数对织物指标的影响结果Fig.2 Effect of number of suspended stitch systems on fabric index

连续成圈针数对织物指标影响结果如图3所示。由图3可知,吊针路数为16路,平针路数为12路时,随着1个组织循环内的连续成圈针数的增加,织物厚度有变化但整体差别较小,因此连续成圈针数对织物厚度的影响较小;连续成圈针数的增加会使织物凹孔的孔口变宽,导致织物的克罗值逐渐下降,一定程度上影响凹孔承托空气,从而降低织物保暖性能。

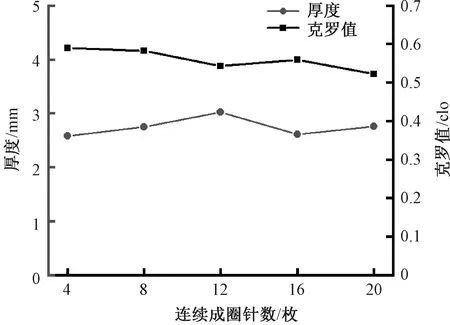
图3 连续成圈针数对织物指标影响结果Fig.3 Effect of number of consecutive coils needles on fabric index

平针路数对织物指标影响结果如图4所示。由图4可知,在吊针路数为16路、连续成圈针数为12枚的情况下,随平针路数的增加,织物厚度及克罗值均减小。由此说明改变1个组织循环内的平针路数会改变织物3D凹孔的密度,且随平针路数的增加,凹孔间距增加孔洞逐渐稀疏,织物的厚度逐渐减小,使得其保暖性下降。

图4 平针路数对织物指标影响结果Fig.4 Effect of number of plain stitch systems on fabric index

3.2 多因素试验结果与分析

根据第3.1小节中单因素试验分析结果,确定表2的多因素试验自变量及其水平表,在此基础上,采用Design Expert8.0软件设计得到17个响应曲面 Box-Behnken 试验方案(见表4),其中响应值分别为织物厚度和织物克罗值。

表4 Box-Behnken 试验的相关参数Table 4 Parameters of Box-Behnken experiment

3.2.1 回归方程及方差分析

对表4中3个因素(吊针路数、 连续成圈针数、平针路数)试验结果进行响应面分析,经过二次回归拟合得到厚度的回归模型如式(1)所示。

δ=0.146 77A-0.031 38B-0.197 63C-8.465 3×10-4AB+8.59 03×10-4AC+

5.781 9×10-3BC-9.888 5×10-4A2-2.513 7B2+2.91C2+2.5

(1)

式中:δ为织物厚度,mm;A为吊针路数,路;B为连续成圈针数,枚;C为平针路数,路;AB表示吊针路数和连续成圈针数的交互作用;AC表示吊针路数和平针路数的交互作用;BC表示连续成圈针数和平针路数的交互作用。

对式(1)进行显著性分析结果见表5。由表5可知,该拟合方程模型显著水平P值为0.000 3<0.050 0。失拟项的P值为0.098 1>0.050 0,试验中无失拟项存在;模型的决定系数R2为0.965,大于0.950,说明模型达到显著水平,因此模型可信程度较高,能较好的地反应实际情况。此外,吊针路数(A)的P值小于0.000 1,达到极显著水平;平针路数(C)的P值为0.006 5<0.050 0,达到显著水平;连续成圈针数(B)的P值为0.073 3>0.050 0,未达到显著水平。研究表明单个因素中吊针路数对织物厚度有极显著影响,C对织物厚度有显著影响,而B无显著影响。分析其原因,A直接影响凹孔的孔洞深度,从而对织物厚度有极显著的影响。而C会改变孔洞的排列疏松度,在一定范围内,孔洞排列越紧密,织物厚度越厚,反之C超过一定数量后,织物厚度会降低,C对织物厚度的影响可能与吊针路数有关。而B改变凹孔孔口口径的大小,一定程度上对织物的影响不明显。此外,BC的P值为0.029 6<0.050 0,说明B与C交互作用对织物的有显著影响。

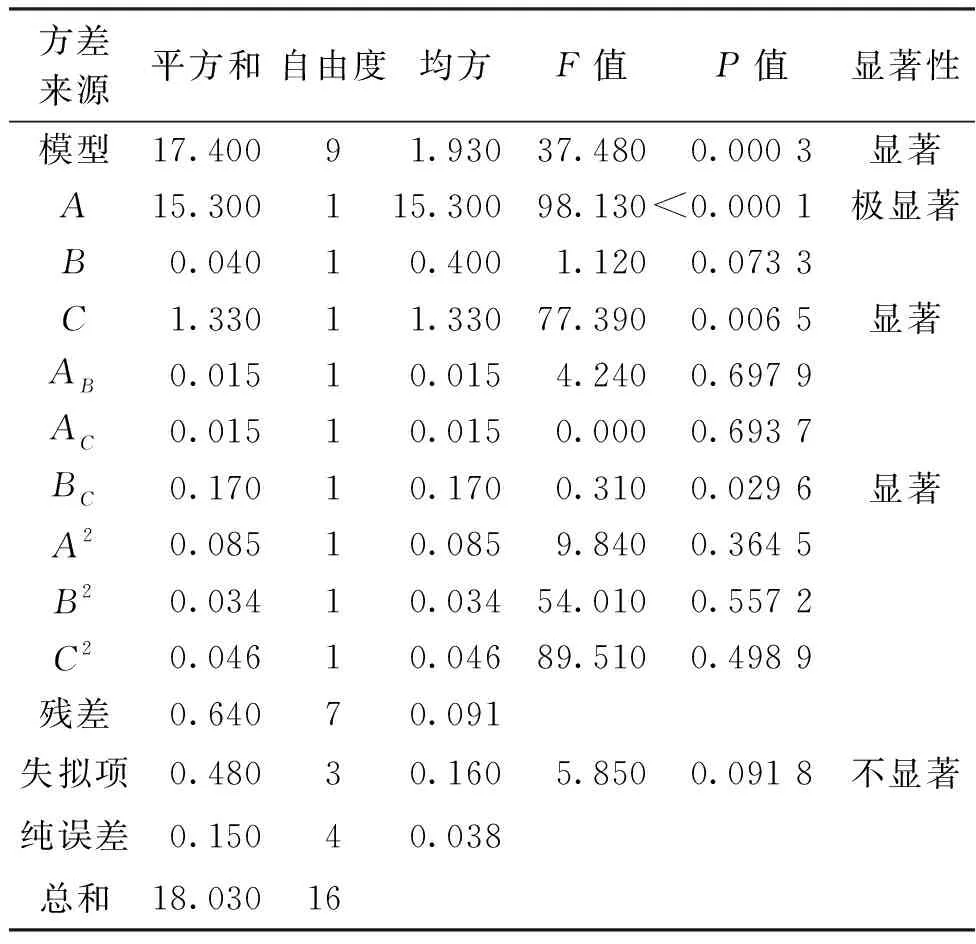
表5 厚度回归模型方差表Table 5 Variance tables of the thickness regression model

经过二次回归拟合得到克罗值的拟合方程如式(2)所示:

Rclo=0.026 6A-0.062 5B-0.105 3C-3.75×10-4AB+3.298 6×10-4AC+1.291 6×10-3BC-4.142×10-3A2+3.336 2×10-4B2+3.662 6×10-3C2+1.138 6

(2)

对该回归模型方程进行分析得出回归方差表见表6,如表6的显著性分析可知,本试验所用的二次多项式显著(P值为0.000 5<0.050 0),失拟项P值为0.091 8>0.050 0,试验模型的决定系数R2为0.957>0.950,说明模型达到显著水平,失拟项差异不显著,表明试验中无失拟项存在,能够较好的反应实际情况。通过对模型系数显著性检验发现,B、C、BC、B2、C2对克罗值的影响显著(P<0.050 0),A对克罗值的影响为极显著(P<0.000 1),除此之外其他因素得到的效应不显著。同时对比F值可以发现,A、B、C3个自变量对织物克罗值的影响次序为:A>C>B,说明A会直接改变凹孔深度从而对3D凹孔织物保暖性的影响最大,其次C会直接改变凹孔密度从而影响织物保暖性。连续成圈针数B决定凹孔孔口宽度,在第2.3节所述测试环境下B对织物保暖性影响最小。

表6 克罗值回归模型方差表Table 6 Variance tables of clo regression models

3.2.2 响应曲面交互作用分析

吊针路数和连续成圈针数的交互作用对克罗值的3D响应图如图5所示。吊针路数(A)和连续成圈针数(B)的交互作用对克罗值有影响,但未达到显著水平,随着吊针路数(C)增加织物克罗值增大,与单因素分析结果一致;而随连续成圈针数增加,织物克罗值呈现先增加后减小的抛物线关系,且随着吊针路数区间增大,抛物线的曲率有所增加。

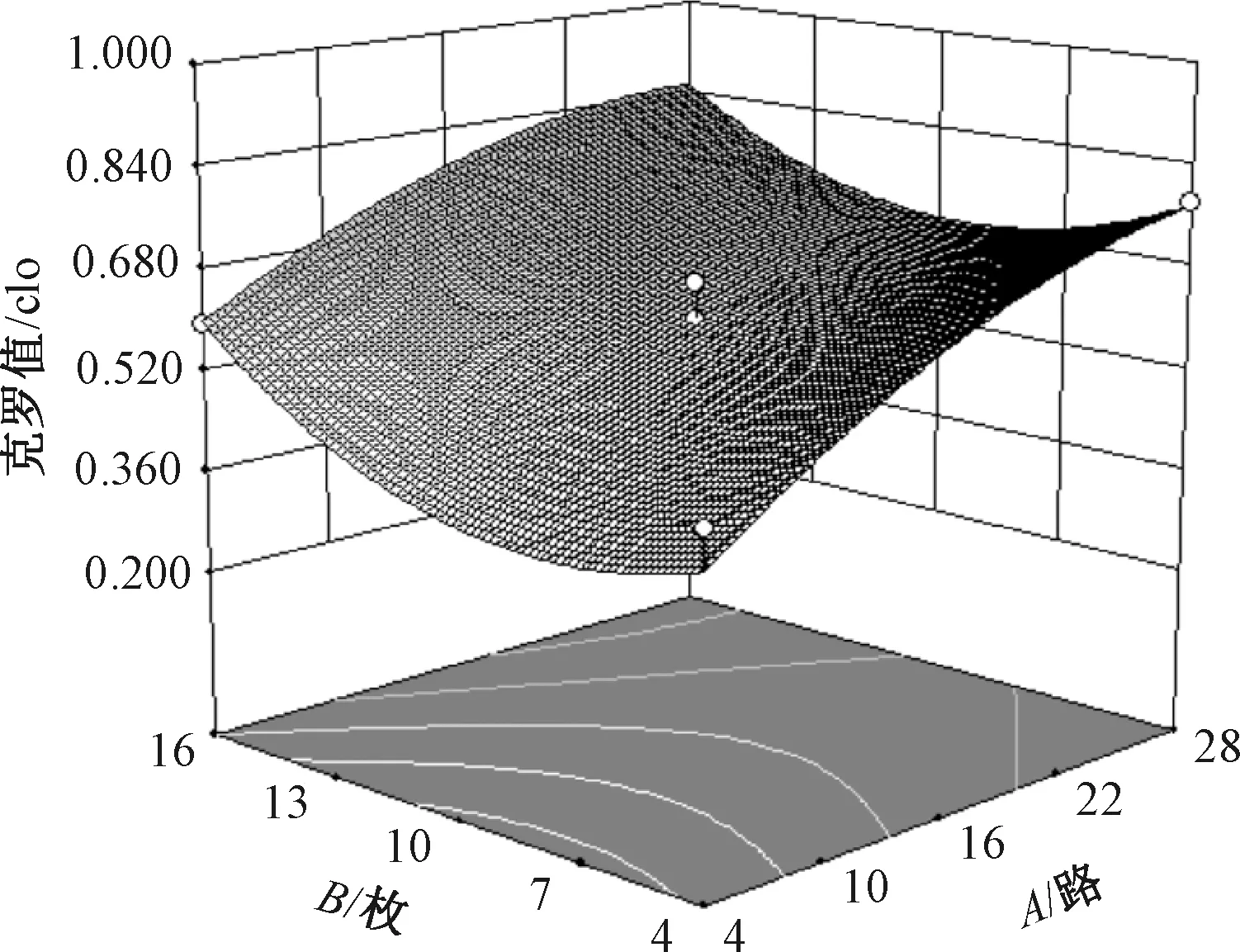
图5 吊针路数和连续成圈针数的 交互作用对克罗值的3D响应图Fig.5 3D response diagram of interaction on clo value between the number of supended stitch systems and the number of consecutive coils needles

吊针路数和平针路数的交互作用对克罗值的3D响应图如图6所示。由图6可知,随着吊针路数的增加织物克罗值增大,与单因素分析结果一致;而随平针路数的增加,织物克罗值呈现先减小后增加的抛物线关系,且随着吊针路数的区间增大,抛物线的曲率有所增加。这表明由于3个因素会相互影响,单因素试验时变量值的选择会影响变量分析结果,因而本研究的多因素交互作用分析的结果比单因素分析更接近真实情况。

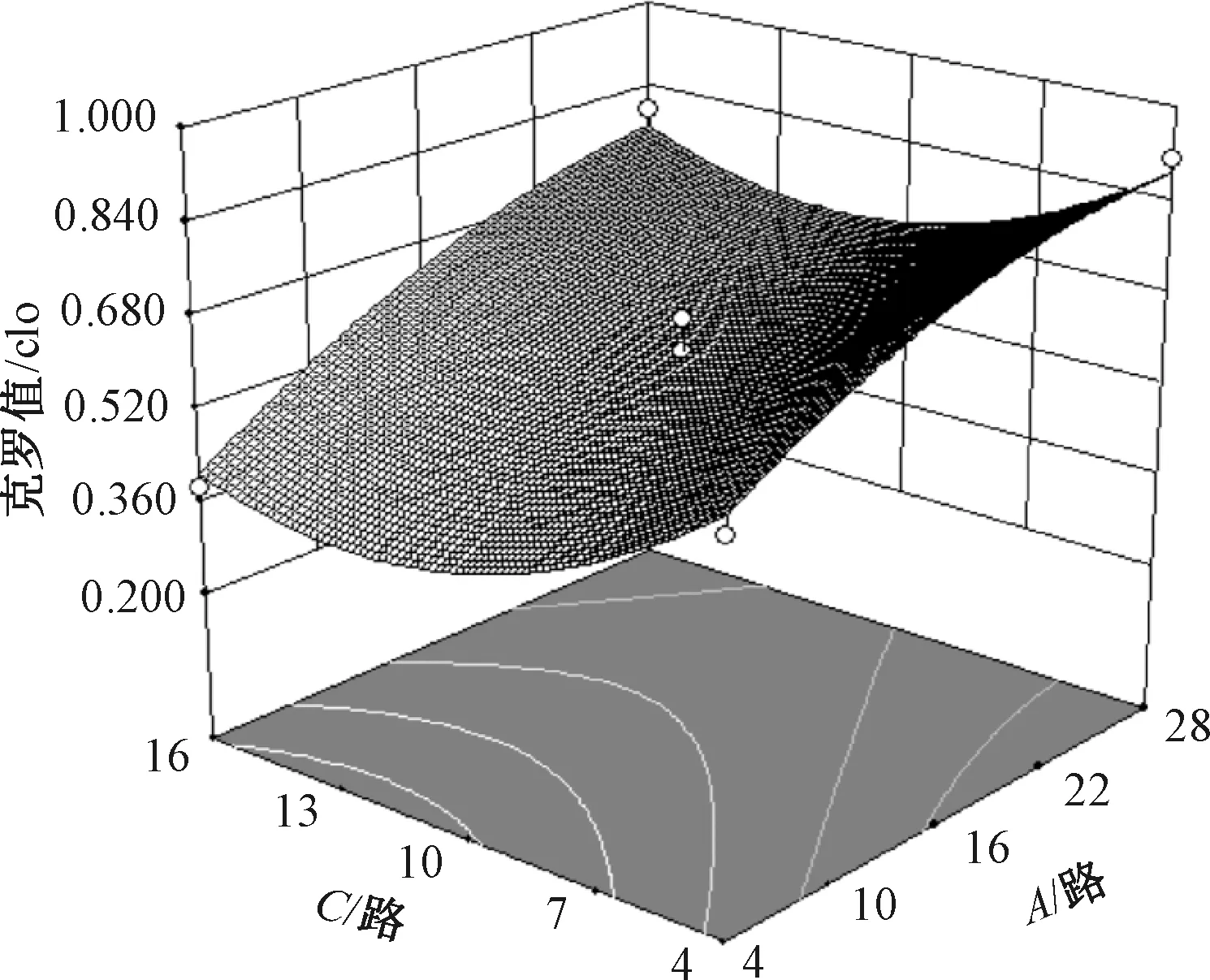
图6 吊针路数和平针路数的交互 作用对克罗值的3D响应图Fig.6 Interaction between the number of suspended stitch systems and the number of plain stitch systems

连续成圈针数和平针路数的交互作用对克罗值的影响3D响应图如图7所示,其中底面等高线的形状趋向于椭圆且椭圆的轴线与坐标轴存在一个角度,表明交互作用明显[12-14]。由图7可知,连续成圈针数与平针路数的交互作用对克罗值的影响显著,与方差分析结果一致。此外,在吊针路数为16路、平针路数为10针左右、连续成圈针数为7针和8针时,织物克罗值最低,说明此参数下形成的孔宽度、密度及深度配比下其织物保暖性较差。

图7 连续成圈针数和平针路数的 交互作用对克罗值的影响3D图Fig.7 3D response diagram of interaction on clo value between the number of supended stitch systems and the number of plain stitch systems

3.2.3 模型的验证及使用

根据式(2)的回归模型,使用Design Expert8.0软件计算出表4试验参数的最优保暖性方案。方案中,吊针路数为16路,连续成圈针数为16枚,平针路数为4路时,织物的克罗值为0.957 clo。再利用式(1)计算出织物厚度预测值为2.917 mm。同样,在该参数条件下,进行织物织造验证试验,测得织物的克罗值为0.942～0.993 clo, 厚度为2.903～2.987 mm,克罗值的误差为-1.5%～3.7%,厚度误差为-0.48%～2.3%。由此说明可以通过响应曲面分析得到经验参数的最优保暖性参数。此外,使用该模型进行响应曲面分析,该模型会根据拟合方程给出多组3种参数条件下的响应值预测,实际应用时,可根据需要优先选出厚度与克罗值配比最合适的参数条件,从而有效减少试验次数,为该3D凹孔结构在不同面料使用场景中提供参考。

4 结 论

使用SANTONI MF8-CHN单面电子提花针织圆机,以双股70 dtex DRYAERN®纱线作面纱,50 dtex DRYAERN®纱线包覆17 dtex氨纶作底纱,将设计的15种不同组织结构参数的3D凹孔针织物进行织物厚度及克罗值测试,并基于响应面对试验结果进行分析,得出以下结论:

1)改变纬编针织圆机中的吊针结构与平针结构的组合,不仅会影响织物外观风格,还对织物的保暖性能有显著影响,其中一个组织循环内吊针路数、连续成圈针数、平针路数对织物保暖影响程度大小为吊针路数>平针路数>连续成圈针数。一个组织循环内连续成圈针数与平针路数的交互作用对织物保暖性影响显著,当连续成圈针数为16路、连续成圈针数为10针左右、平针路数为7～8针时,织物克罗值处于较低水平,保暖性相对较差。

2)采用Design Expert8.0软件,按照Box-Behnken 原理设计响应面试验,设响应值为织物厚度和克罗值,并对试验结果进行二次拟合得出多个响应值的回归模型。结果表明:织物厚度及克罗值的模型拟合精度较高,可较真实的反映实际情况;模型得出织物保暖性最佳的组织结构设计方案为吊针路数16路、连续成圈针数16枚、平针路数4路,织物克罗值为0.957 clo, 保暖性较好。

在实际应用中,根据织物厚度、克罗值的拟合方程综合选择出适宜的参数方案,以满足服装对织物厚度、风格与保暖性的综合要求。