Boussinesq方程的孤子与Jacobi椭圆函数波的相互作用解及动力学研究
刘 鹏, 向靖峰
(贵州师范大学物理与电子科学学院, 贵阳 550025)
寻找非线性偏微分方程的解析解有助于解释复杂的非线性物理现象, 非线性偏微分方程解析解的研究受到了许多数学家和物理学家的关注.随着非线性研究的发展, 数学家和物理学家提出了很多有效的方法,例如分离变量法[1]、反散射法[2]、Bäcklund变换[3]、Hirota双线性变换法[4]、齐次平衡法[5]等,这些方法可以获得非线性偏微分方程的孤立波解.随着计算机技术的发展与非线性研究的深入, 计算机符号计算成为求解非线性偏微分方程的有力手段之一. 2000年,范恩贵[6]基于Riccati方程的精确解, 提出tanh函数展开法. 2001年, 刘式适等[7]提出了比Tanh函数展开法更通用的Jacobi椭圆函数展开法, 用于构造非线性波动方程的精确周期解. 2015年, 楼森岳[8]利用Riccati方程, 提出了求解非线性系统的相容的Riccati展开方法,即CRE方法, 该方法可根据非线性偏微分方程的CRE可解性条件来构造新的相互作用解.
1872年, 法国物理学家Boussinesq提出了著名的Boussinesq方程来解决两个方向的浅水波运动问题.该方程为:
utt+αuxx+β(u2)xx+γuxxxx=0,
(1)
其中, 下角标x和t表示偏微分. Boussinesq方程主要用来研究等离子体物理、固体物理和流体力学等领域的物理现象[9]. 目前, 已经有很多报道寻找Boussinesq方程精确解的有效方法. 例如, 文献[3]利用Bäcklund变换得到Boussinesq方程的孤子解和周期波解. 文献[10]利用Riccati展开法得到了Boussinesq方程的孤立波解和三角函数解. 文献[11]利用F展开法得到Boussinesq方程的多种精确行波解. 文献[12]使用雅可比(Jacobi)椭圆函数展开法得到Boussinesq方程的Jacobi椭圆周期波和孤立波解. 文献[13]基于齐次平衡法给出了Boussinesq方程新的精确解, 并且研究了方程的混沌行为. 以上的这些方法没有得到孤立波与Jacobi椭圆周期波的相互作用解. 本文将楼森岳教授提出的CRE方法应用于Boussinesq方程, 得到了孤立波与Jacobi椭圆周期波的相互作用解, 通过改变Jacobi椭圆函数的模数得到了相互作用解的不同动力学行为, 并作图说明了这种复杂解的物理意义.
1 CRE方法简介
考虑一个非线性偏微分方程
p(t,x1,x2,…,xn,u)=0,
(2)
设方程(2)有如下形式解
(3)
这里,u与w是关于x,t的函数;N为正整数,其值由方程(1)中的非线性项和最高阶导数项平衡得到;R(w)是Riccati方程的严格解[8].Riccati方程的形式为
Rw=σ+R(w)2,
(4)
这里,Rw表示(dR(W))/dw,σ是常数.将(3)式和(4)式代入(2)式, 得到关于R(w)的方程, 并令R(w)各阶次项的系数为零,求解得出ui的关系式,再将ui代入(3)式中进行求解就可以得到方程(2)的解.再令R(w)各阶次项的系数为零,过程中得出方程数量多于未知数个数的情况,由此得到的代数方程组为超定方程组,解该超定方程组得到方程(2)的相容性条件
F(w)=0.
(5)
因此,只要方程(5)有解w(x,t), 将解w(x,t)代入(3)式中就可以得到方程(2)的解,即方程(5)是自洽的,说明非线性偏微分方程(2)是CRE相容系统[14].CRE方法可应用于证明一个系统为相容系统,并适用于寻找一个非线性系统的相互作用解.
2 Boussinesq方程的奇异孤立波解和三角函数波解
考虑形如(1)式的Boussinesq方程, 设其形式解为(3)式, 通过平衡非线性项和最高阶导数项得到N=2, 由此得到方程(1)的截断展开解为
u=u0+u1R(w)+u2R(w)2,
(6)
这里,u0,u1,u2和w是关于x,t的函数,R(w)是方程(4)的解,方程(4)含5个特解[15].
当σ<0时,
(7)
(8)
当σ>0时,
(9)
(10)
当σ=0时,
(11)
将(6)式和(4)式代入方程(1)中,从而得到关于R(w)的方程:
R(w)2u2tt+mu1wtt+2mR(w)u2ttwtt+
R(w)2u2xx+mu1wxx+2mR(w)u2wxx)+
2β((u0x+R(w)(u1x+R(w)u2x)+
m(u1+2R(w)u2wx)2+(u0+R(w)(u1+
R(w)u2))(2mu1xwx+4mR(w)u2xwx+
6R(w)4(6wx(2u2xwxx+wx(u2xx+u1wxx))+
4wx(6σu2xwxx+u1xxx)+
4wx(24σu2xwxx+u1xxx)+
(12)
其中,m=σ+R(w)2.
令方程(12)中R6系数为零,可得
(13)
令方程(12)中R5系数为零,可得
(14)
令方程(12)中R4系数为零,可得
(15)
令方程(12)中R3系数为零,并将式(13)~(15)代入,可得
(16)
将式(13)~(16)代入方程(12),求得Ri(w)的系数,应用软件mathematica 12.0验证其系数均为零.所以, 方程(1)是CRE方法可解的.(16)式是Boussinesq方程的相容性条件,只要证明w是方程(16)的解,则方程(1)有解
(17)
构造方程(16)有如下行波解
w=k1x+w2t,
(18)
这里,w是关于x,t的函数,k1,k2为任意常数.
由式(17)、 (18)和(7)可得孤立波解

(19)
由式(17)、 (18)和(8)可得奇异孤立波解

(20)
由式(17)、 (18)、 (9)和(10)可得三角函数波解
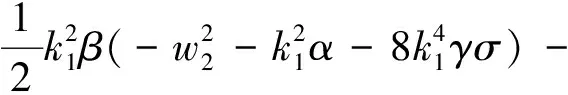
(21)
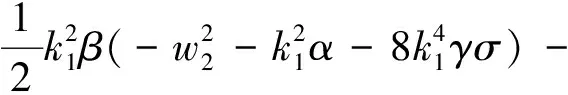
(22)
3 Boussinesq方程的孤立波-周期波相互作用解
由方程(1)的CRE性质,可构造该方程孤立波与Jacobi椭圆函数周期波的相互作用解.设(16)式的形式解为
w=k1x+w1t+F(k2x+w2t),
(23)
其中,k1,k2,w1和w1为任意常数.且令
F(k2x+w2t)=F(ξ)=F,
(24)
其中,F满足第一类椭圆函数方程
(25)
这里,F1=Fξ;C0,C1和C2是常数.当
C0=1,C1=-(1+k2),C2=k2,
(26)
方程(25)存在特解[16]
F1=sn(ξ,k),
(27)
其中,sn表示Jacobi正弦函数,k(0 (28) 这里,令Fξ的各阶次项系数为零,可以解得 (29) 将(26)式代入(29)式,可以得出(28)式成立的条件, (30) 这里,k1,k2和w2是不全为零的任意常数.如上式(30)成立,则根据式(23)~(27),方程(16)有特解 (31) 其中,cn表示Jacobi余弦函数,dn是第三种Jacobi正弦函数[16].由(31)式可知σ<0,满足Riccati方程的特解为式(7)和(8).将上式(31)和(7)代入方程(17),同时取C=0,从而通过求解得出方程(1)的一个孤立波和Jacobi椭圆周期波的相互作用解, (32) 基于式(32),如果自由参数取值如下: k2=-0.6,k1=0.8,w2=0.5,β=-1, (33) 可以得到孤立波-Jacobi椭圆周期波相互作用解的空间结构和时间演化,如图1所示.不同颜色曲线表示模数取值不同, 其取值分别为k=0.001(绿色),k=0.5(红色),k=0.999(蓝色).图2是图1对应的时-空演化图及其密度图.从图1(a)结构图可以看出,k=0.001(接近模量下限0的值), 相互作用解u退化为单个钟型孤立波, 且幅度数值只接近1.808; 当k=0.5, 相互作用解u表现出含周期波的孤立波, 且幅度数值达到10左右.从图2可看出, 当k=0.001和0.5时, 孤立波-Jacobi椭圆周期波相互作用随时间变化的过程中,振幅几乎保持不变, 体现了孤子能量守恒的性质.但当k=0.999(接近模量上限1的值)时, 从图1(a)和图2(c)看出u呈现出周期型变化,但从密度图2(f)可以看出, 孤立波-Jacobi椭圆周期波相互作用导致了波形和幅度发生了变化. 本文用CRE方法求解Boussinesq方程, 得到Boussinesq方程的相容性方程(16), 说明该非线性方程CRE可解.通过构造相容性方程(16)的不同形式解, 得到了Boussinesq方程单孤子解, 以及孤子与Jacobi椭圆正弦周期波的相互作用解.进一步, 作图说明了在不同模数k条件下, 孤子与Jacobi椭圆正弦周期波的相互作用解的结构,以及随时间演化的动力学行为. Boussinesq方程是一个著名的孤立子方程, 应用于众多科学领域, 本文结论有利于深入认识该方程的物理意义.
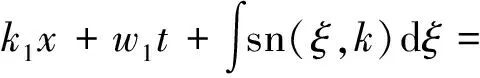
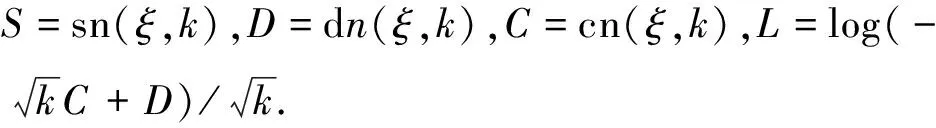
4 结论

