正负电子对撞中类底夸克偶素的线形*

叶全兴 何广朝 王倩†

1)(华南师范大学量子物质研究院,原子亚原子结构与量子调控教育部重点实验室,广东省高等学校物质结构与相互作用基础研究卓越中心,广州 510006)

2)(华南师范大学南方核科学计算中心,粤港量子物质联合实验室,广东省核物质科学与技术重点实验室,广州 510006)

在重夸克自旋对称性下构造量子数为 JPC=1-- 的P波有效相互作用势,代入李普曼-史温格方程求得e+e- →的散射振幅,发现对应的散射截面可以解释现有的实验数据.研究发现底夸克偶素的质量移动很小,主要是由于底夸克偶素和道的有效耦合比较小.因此,e+e- →截面上的峰结 构主要是 Υ(4S),Υ(3D),Υ(5S)和Υ(6S) 的贡献.能量在 10.63 GeV 处的窄峰 值结构需要实验 上进一步细致扫描和理论上拟合公式的优化.

1 引言

强相互作用是自然界中四种基本相互作用之一,是将夸克和胶子形成色单态强子的最主要相互作用.描述强相互作用的基本理论是量子色动力学,其低能色禁闭的性质决定实验上能直接观测到的粒子都是色单态的强子,因此,研究强子的内部结构和性质是理解强相互作用最重要的手段之一.1964年,盖尔曼[1]提出强子是由更基本粒子(称为夸克(quark))所组成.同年,茨威格[2]在他的书中也提出相同的概念,并将这种基本粒子命名为“aces”.这些概念的提出也标志着夸克模型的建立.

夸克模型将强子分为介子和重子,介子由夸克和反夸克构成,重子由3 个夸克构成.另一方面,量子力学色动力学的色禁闭性质允许除上述两种构型外的其他色单态强子(即多夸克态)的存在.因此,高能实验物理学家致力于寻找多夸克态.直至2003年,实验上发现第一个奇特强子态候选者X(3872)[3]的信号,打开了实验上研究奇特强子态的大门.迄今为止,实验上发现了几十个超出传统夸克模型的奇特强子态候选者,它们内部结构有多种解释:强子分子态、三角奇异性带来的运动学效应、紧致多夸克态、混杂态等[4-14].这些奇特强子态的候选者多数都有比较邻近的阈值,因此,有可能是强子分子态的候选者[8],或者是三角奇异性带来的运动学效应[12],例如正负电子对撞中发现的Y(4260) 与的阈值比较接近,可以作为的强子分子态候选者.Y(4260) 的的强子分子态图像可以很好地解释相关的实验数据[15-28],并且预言新的重夸克自旋对称性伴随态粒子[29-33].阈值在正负电子对撞中有重要贡献,主要是因为粲夸克系统具有明显的重夸克对称性破坏效应[17,27].这也说明底夸克偶素能区正负电子对撞过程中,阈值效应没有粲夸克偶素能区中阈值作用贡献重要.另一方面,BelleII 实验组在正负电子对撞的底介子对产生截面中,在阈下没有发现明显的共振态信号[34].与粲偶素能区物理不同,底夸克偶素能区重夸克对称性比较好保持.因此,阈值在底夸克偶素能区正负电子对撞过程中产额不大,所对应的阈值效应不重要.阈值效应是否明显一方面取决于对应道在所研究过程中的产额是否足够大,另一方面取决于阈值对应的两个或多个强子的总宽度是否足够小.因此,研究底夸克偶素能区正负电子对撞过程中的截面,窄共振态的阈值效应起主要作用.本文主要在重夸克对称性下研究底夸克偶素能区正负电子对撞过程中的阈值效应,以及由于它们之间的相互作用是否可以形成对应的强子分子态.

2 理论框架

重夸克极限下,量子色动力学拉氏量可以按照重夸克质量的倒数进行展开.领头阶的拉氏量不依赖于重夸克的自旋和重夸克的质量,即具有重夸克自旋对称性和重夸克味道对称性.这两种对称性是研究含有重夸克系统的重要手段.本文将利用重夸克自旋对称性,研究底夸克偶素能区正负电子对撞到B 介子对的产生截面,以揭示可能的类底夸克偶素态.

2.1 有效势

重夸克自旋对称性下,重轻介子的动力学性质取决于轻自由度.因此,S 波的(或)介子的轻自由度完全由反轻夸克(轻夸克)承担,S 波赝标介子B 和矢量介子 B*构成轻自由度sl1/2-的重夸克自旋二重态(B,B*).由于正负电子湮灭为一个虚光子,具有JPC1--量子数.因此,具有JPC1--的量子数的 P 波才能在正负电子对撞中产生.为构造 P 波的有效相互作用势,首先考虑 P 波的重轻分解,

为了简化式子,上面等式右面省略了下角标 1--.由于重轻分解的变换是幺正变换,因此这些波函数是正交归一的[36].下标 1--表示正负电子对撞中产生的B 介子对的量子数JPC.上标s0,s2表示两强子系统的总自旋.这四个道分别用拉丁指标i,j=1,2,3,4 表示.

低能情况下,C0,C1,C2视为常数.根据上述定义,双B 介子系统在量子数为 1--的接触势为

因为 4×4 的接触势是对称矩阵,所以此处只给出上半对角的矩阵元.原则上,在能量区间比较大的情况下,即动力学道对应的三动量可以和π 介子质量相比时,需要引入单π 交换势.但是文献[37-40]中对强子分子态的研究表明,引入单π 交换势时的物理性质与只考虑接触势时的物理性质基本一致,因此,本文计算只考虑接触势的贡献.

实验上测量的质心系能量在[10.55,11.03]GeV之间,夸克模型的计算表明此能量区间可能存在4 个裸态[41],分别是 Υ(10580),Υ(10753),Υ(10860),Υ(11020).目前这4个态的性质是Υ(10580) 为Υ(4S),Υ(10753) 看作Υ(3D)与Υ(4S,5S) 的混合[42],Υ(10860)和Υ(11020) 则分别看作是Υ(5S)和 Υ(6S)[41,42].因此,4 个裸态在本文中分别为 Υ(4S),Υ(3D),Υ(5S),Υ(6S).并用希腊指标α,β=1,2,3,4 来表示.重夸克极限下S和D波的底夸克偶素分别耦合到|1⊗0〉,|1⊗2〉的重轻基,耦合强度分别定义为

综上所述,以上8 个衰变道的势能矩阵可以写成如下的形式:

其中Vo是4 个开放道对应的势能矩阵,Vob是裸态与的耦合矩阵,Vbo矩阵是Vob 矩阵 的转置.

2.2 李普曼-史温格方程

由于本文所考虑的有效势是常数,因此李普曼-史温格方程可化简为矩阵形式的代数方程:

由于存在8 个衰变道,因此T,V,G均为8×8的矩阵,不妨将T矩阵改写成四块 4×4 的矩阵,表示为

类似地,G矩阵可以改写为两块对角矩阵:

其中Gpdiag(G1,G2,G3,G4),Sdiag(S1,S2,S3,S4).两体传播子

其中mα为第α个裸态的质量.

由于裸态间的跃迁势为零,李普曼-史温格方程可以写为两组 4×4 维的方程组,

第二部分为

将(10)式代入(9)式得:

定义有效作用势为

类似地,可以得到其他的散射矩阵元.

2.3 物理产生振幅及散射截面

相关的8 个道的裸顶点产生振幅定义为

其中fα(α1,2,3,4)是虚光子和相应的底夸克偶素之间的耦合常数,可以通过以下公式进行计算[43]:

fα即为(17)式中的e/fV,αe1/137 是精细结构常数,ΓV→e+e-是矢量介子衰变到 e+e-的衰变宽度,pe是末态电子的三动量.Fi是虚光子和第i个开放道的耦合常数,可以参数化为

物理产生振幅可以通过求解矩阵方程:

获得.将列矩阵F进行分块,表示为

相应地,将列矩阵U进行分块,表示为

求解上述方程可获得:

将(25)式移项化简得:

相应的散射振幅的模方为

(29)—(32)式中角度的贡献在文献[36]中有较为详细的讨论.第i个开放道的微分散射截面为

将(29)—(32)式代入(33)式,对θ从0 到π 积分,即可得到相应开放道的散射截面:

通过拟合实验上 e+e-→过程中的反应截面提取模型中的参数,并进一步提取感兴趣的物理信息.

3 数值结果与讨论

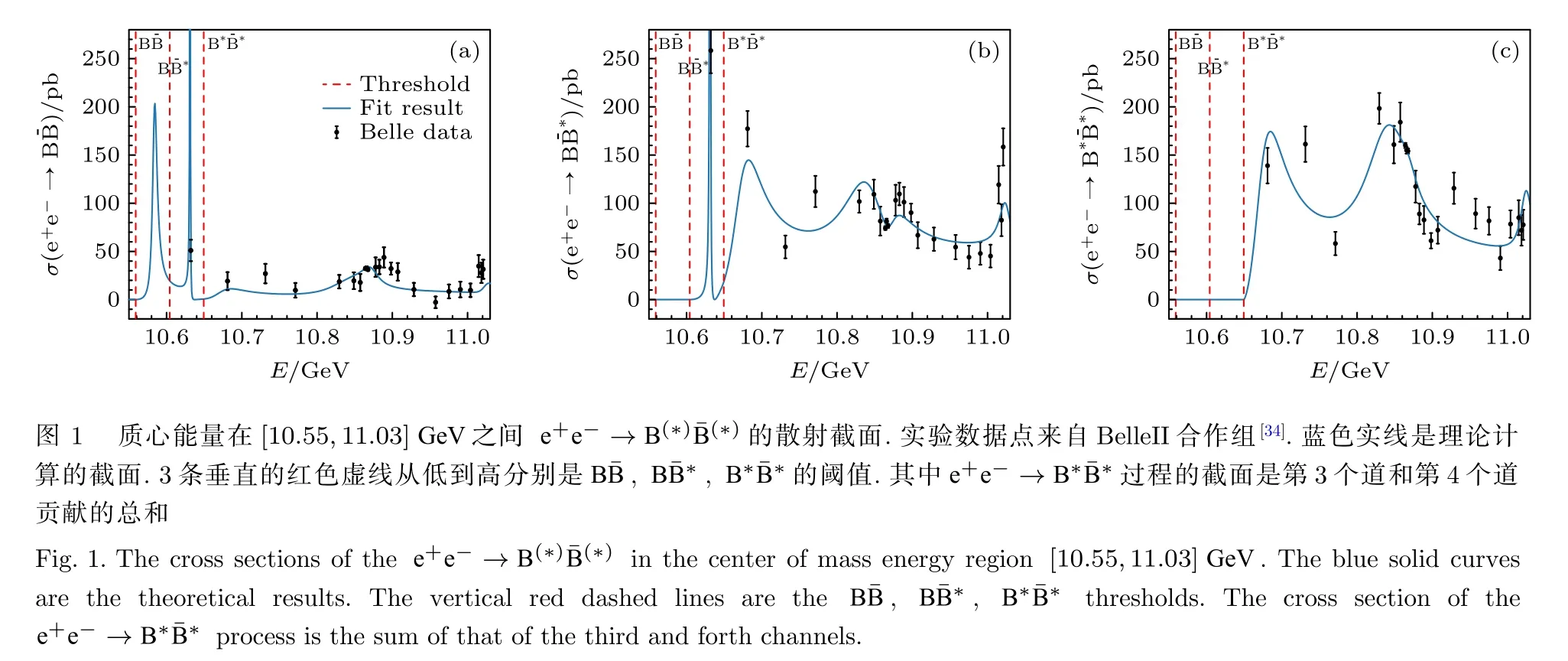
具体的数值计算结果表明,上一节的截面公式可以很好地解释BelleII 合作组最新的截面数据[34],如图1 所示.理论计算结果(图1 中蓝色实线)穿过大部分实验数据点,证明此图像可以很好地解释实验数据.拟合得到的模型参数如表1 所列.

表1 拟合参数和约化卡方Table 1.Fitted parameters and the corresponding reduced χ2.

具体拟合过程中发现参数C0与参数g4S,g5S,g6S,的关联性比较强.这是由于上述参数都与重轻自由度|1⊗0〉耦合,因此,其中一个参数的变化可以被其他参数吸收.同理,由于参数C2与参数g3D,都可以耦合到|1⊗2〉重轻自由度,因此,它们的关联性也比较强.

其中低能有效耦合常数C0,C1,C2的数值大小处于同一个量级,满足有效场论对同一阶参数的要求.4 个底夸克偶素的裸质量位置与截面上峰值的位置偏移较小,他们的偏移是由耦合道效应导致的,由于其耦合强度较小(如表2 所列),导致偏移较小,即 Υ(4S),Υ(3D),Υ(5S),Υ(6S) 的裸质量分别是(10.468±0.043)GeV,(10.856±0.004)GeV,(10.830±0.011)GeV,(11.024±0.008)GeV.这4 个裸态在图1的3 个反应道的截面上都有所反应,即在图1(a)中,分别对应质心系能量在 10.58,10.87和 11.03 GeV 处的峰值.其中 10.87 GeV 处的峰值是由 Υ(3D),Υ(5S) 共同效应导致的结构.由于运动学相空间效应,质心能量在 10.63 GeV 处的尖峰只在 e+e-→,e+e-→过程的截面中有所体现.此尖峰结构主要由这两个反应过程中10.63 GeV附近两个实验数据点决定,统计显著性不高.当进一步考虑实验分辨率的效应,上述尖峰将变得平滑.Υ(3D),Υ(5S),Υ(6S) 在e+e-→和 e+e-→反应过程中均有所体现,即对应10.85和11.02 GeV 附近的峰.拟合对应的极点位置和主要耦合道及其耦合强度列在表2 中.从表中可以看出,所有极点与B 介子对的耦合强度比较小,截面上的峰值结果均是由重夸克偶素导致的.

表2 物理黎曼面 R+++,离物理黎曼面近的黎曼面 R-++,R-+,R--- 上的极点(第2 列)和主要耦合道及其有效耦合常数(第3 列)Table 2.Poles on the physical sheet R+++,those R-++,R-+,R--- close to the physical one(the second column),the dominant channel with the corresponding effective coupling(the third column).

4 总结与展望

BelleII 国际合作组测量了 e+e-→的散射截面实验数据,并且通过高阶切比雪夫多项式对实验数据进行了拟合.本文在重夸克自旋对称性下,构造量子数为JPC1--的P波散射势,代入李普曼-史温格方程,并通过代数求解李普曼-史温格方程得到物理散射振幅,进而求出e+e-→过程的散射截面.通过拟合BelleII的实验数据发现,底夸克偶素 Υ(4S),Υ(3D),Υ(5S)和 Υ(6S) 在随质心能量依赖的线形中体现为 10.58,10.87和11.03 GeV 处的峰值.其中10.87 GeV峰值是由 Υ(3D)和Υ(5S) 两个底夸克偶素共同作用的结果.质心能量在 10.63 GeV 处的峰值附近只有两个能量点,此处峰值的性质一方面需要实验上进一步细致扫描,另一方面需要理论公式中考虑实验上的分辨率并且做Bin-by-Bin 拟合.因此,为进一步确定 10.63 GeV 附近底夸克偶素的性质,需要实验上在此能区内做进一步细致扫描.

感谢电子科技大学杜孟林教授的早期工作和讨论.