石墨烯类超导体的单磁性杂质效应*

赵宗阳 李铭 周涛

(华南师范大学物理学院,广东省量子调控工程与材料重点实验室,粤港量子物质联合实验室,广州 510006)

超导体的磁性杂质效应以及其中存在的束缚态(即Yu-Shiba-Rusinov 态)一直受到较多的关注.最近,在实验室中,成功发现了石墨烯类超导材料中Yu-Shiba-Rusinov 态的存在.本文在实空间建立描述石墨烯材料超导态的有效哈密顿量,考虑单个磁性杂质,构造Bogoliubov-de Gennes(BdG)方程,并对超导序参量做自洽计算,在此基础上,理论研究了石墨烯类超导体的磁性杂质效应.计算结果显示,仅当超导的配对对称性是传统的s 波配对时,能隙内会出现Yu-Shiba-Rusinov 束缚态,束缚态的位置以及强度和杂质的磁矩有关,且强度显示出了明显的正负非对称性,但对于p+ip 和d+id 配对对称性,则不存在能隙内的束缚态.本文的理论计算结果一方面对实验现象做了合理解释,另一方面指出了石墨烯和传统超导组成的异质结系统,石墨烯层由于临近效应诱导出来的超导配对项仍然是s 波配对.

1 引言

由于二维的石墨烯材料具有独特的物理特性以及广阔的应用前景,近20 年来其物理性质受到了广泛的关注[1].一个重要的研究方向是在石墨烯类材料中实现超导电性.理想的石墨烯材料是一种半金属材料.没有超导电性,但近年来在实验室中已通过多种辅助途径在石墨烯类材料中成功实现超导电性,有效的手段包括:通过插入其他原子层的方法实现超导电性[2,3],在双层和三层石墨烯材料中通过外加电场和磁场的方法诱导出超导电性[4,5],在双层和三层魔角石墨烯中实现超导电性[6,7],以及用超导材料和石墨烯材料构成异质结,通过邻近效应在石墨烯材料中实现有效的超导配对项[8,9].

对于超导体材料,一个核心的研究内容是探索其配对对称性.对于石墨烯类超导体,过去十几年来,很多研究组理论探索了它可能的配对对称性.目前主要候选配对对称性是p+ip 配对[10,11]和d+id 配对[12-15].另一方面,对于超导体和普通金属组成的异质结系统,由于邻近效应,通常会在普通金属材料中诱导出有效的超导配对项.一般认为,诱导出的超导配对项对称性应与原超导体的配对对称性相同.但是,在石墨烯材料中,实验测量得到结果却并非必然如此.实验中,将石墨烯材料放在电子型掺杂铜氧化合物超导体Pr2-xCexCuOx上形成异质结,通过扫描隧道光谱实验得到其局域电子态密度的信息,结果显示石墨烯中诱导出了p 波对称性[9],而原铜氧化合物超导体却是d 波对称性,两者的配对对称性并不相同,因此,即使对于石墨烯-超导的异质结系统,其配对对称性也是一个值得研究的课题.

杂质效应往往可以用来作为判断超导体配对对称性的有力工具,比如在某些对称性下,杂质可以导致能隙内的束缚态[16].在过去几年,理论研究者对石墨烯材料中的杂质效应有过一定的关注[17-19],其中的束缚态的存在被建议可以用来判断石墨烯材料的配对对称性.而本文主要关注石墨烯超导体的磁性杂质效应.事实上,超导体中的磁性杂质效应一直是一个重要的研究方向,早在1960 年代,于禄[20],Shiba[21]和Rusinov[22]分别独立地通过理论计算提出超导体中磁性杂质周围会存在能隙内的束缚态,Yu-Shiba-Rusinov态(简称为YSR 态).需要指出的是,YSR 态与杂质原子的局域磁矩密切相关,所以YSR 态背后的物理原因与上述非磁性杂质诱导出的束缚态完全不同[16-18].1997年,YSR 态的存在被实验证实[23].在石墨烯类超导体中,理论预测可以通过氢化的方法引入局域磁矩,进一步的计算预测了YSR 态的存在[24].最近,实验上对石墨烯类超导体的YSR 的观测也有了进展,在一个石墨烯和传统的铅超导体的耦合系统中,在晶界附近观测到了YSR 态的存在[25].

理论计算显示,在石墨烯材料的晶界附近会引入磁性的点缺陷[26-28],因此,理论上可以通过单个磁性杂质附近的局域电子结构来定性模拟晶界附近的电子结构并进一步研究YSR 态.对超导体的单个杂质效应的研究通常有两种有效的方法,一种是忽略杂质对超导序参量的影响,近似认为超导序参量均匀分布,将哈密顿量分为均匀项和杂质项两个部分,其中均匀部分可以进行傅里叶变换到动量空间,杂质项可以视作微扰或者一个散射中心处理,在T 矩阵或者微扰论结合戴逊方程的基础上获得系统的格林函数,进一步可以研究系统的其他性质[16,17,24].这种方法的缺点是忽略了序参量的空间涨落,尤其是我们通常关心杂质附近的局域特性,而杂质附近的超导序参量往往被压制了.优点是格林函数有很好的解析形式,可以根据格林函数分母的零点分析能隙内束缚态产生的原因,且在动量空间处理问题,不存在尺寸效应.

早期,针对石墨烯超导态,有研究组运用T 矩阵的方法研究了单个磁性杂质效应[19],计算结果表明:仅仅在杂质原子的磁交换作用大于石墨烯的能带宽度时,YSR 态才出现.这一条件在实际材料中比较难满足.但是由于T 矩阵方法忽略了杂质对超导序参量的压制,所以该方法虽然可以定性地研究杂质效应,但是,杂质的作用有可能会被低估.理论上存在着另一种研究杂质效应的方法,就是实空间的 BdG 方程方法[18,29,30],采用这种方法需要在实空间写出整个哈密顿量,自洽求解实空间所有格点的超导序参量,进一步用实空间对角化的方法求解系统的实空间格林函数.这种方法的缺点是只能在有限大小的系统中计算,具有一定的尺寸效应,且没有办法进一步理论分析束缚态产生的原因,优点是进行了全空间对角化,且充分考虑了杂质对序参量的影响,结果较为精确.在过去石墨烯超导体的非磁性杂质的理论研究中,这两种方法都被采用[17,18],结果定性上大体相同,但细节处仍然有较多的差异.

本文采用了实空间BdG 方程的方法结合自洽计算来对石墨烯材料的磁性杂质效应进行理论研究.由于实验上YSR 是在石墨烯和传统超导体耦合系统中发现了YSR态,可判断该实验中石墨烯材料诱导出的配对对称性有比较大的概率也是传统的s 波配对.所以本文主要研究也是基于传统的s 波配对.计算结果显示,s 波配对的石墨烯超导体具有明显的YSR 束缚态,其性质定性符合实验结果.另一方面,也研究了p+ip 和d+id 配对的石墨烯超导体的磁性杂质效应,计算结果和s 波配对有非常大的区别,对于这两种配对对称性,并没有出现明显的YSR 态.结果一方面表明,磁性杂质效应可以作为判断石墨烯类超导体配对对称性的一个有力的工具,另一方面,和最近发表的实验结果相比较,本文结果说明,石墨烯和传统超导体组成的异质结其邻近效应诱导出来的石墨烯中的超导配对仍然是传统的s 波配对.这一结果有别于石墨烯-电子型铜氧超导体异质结的情况.

2 理论模型

我们的出发模型包含正常态项、超导配对项和磁性杂质项,总的哈密顿量可表示为

其中,tij表示i格点和j格点之间的跳跃,实际计算中,取最近邻格点之间的跳跃,σ表示电子的自旋,μ是化学势.

如果是d+id 或者p+ip 配对,超导配对项可表示为近邻格点之间的配对：

〈ij〉表示j格点在i格点的最近邻.

Js为杂质点自旋和石墨烯格点上传导电子的交换耦合常数[29,30].

考虑实空间共有N个格点,超导态总的哈密顿量可以写成 2N×2N的矩阵形式,可以列出如下的BdG 方程:

其中,Hij-tij-µδij,来自正常态哈密顿量的贡献,如果是d+id 和p+ip 配对,配对项需满足额外的约束条件,即ΔjiξΔij,其中,ξ+1 或者ξ-1,分别对应d+id 配对和p+ip 配对.ujm和vjm是哈密顿量矩阵的本征矢中的分量,Em是哈密顿矩阵的本征值,均可通过对角化哈密顿量矩阵求得.

根据BdG 方程,可以自洽地求解超导序参量,如果考虑超导项是起源于同一个格点上的电子间的有效吸引相互作用,吸引势为V,这种情况是s 波配对,自洽方程可以表示为

对于p+ip 配对和d+id 配对,超导项是来自最近邻格点之间的有效吸引相互作用,同样考虑吸引势为V,自洽方程可以表示为

在自洽地求解得出每一个格点的超导序参量之后,可以进一步计算格点上的粒子数ni,以及局域磁矩mi,由于自旋磁矩和自旋角动量成正比,可采用自旋角动量z方向平均值Sz表示局域磁矩:

最后,可以得出格点i处的局域电子态密度ρi(ω)的表达式:

在下文计算结果展示中,取最近邻格点的跃迁常数为能量的单位,即tijt1(i和j为最近邻格点).在自洽计算中,配对势V的大小决定了超导能隙的大小,两者是单调递增的关系.通常来说,超导能隙大小不改变杂质效应的定性行为,但是超导能隙越小,Γ就需要越小,这样才能使得能隙内的特征被更好的展示.但是Γ太小,会使得LDOS 曲线急剧振荡,所以,通常理论计算会取一个相对大的配对势,这样Γ也可以取得较大,使得曲线平滑且能隙内的特征更加明显[17],本文取V2.15和Γ0.01.化学势取值决定了电子浓度的大小,由于实验中运用邻近效应在石墨烯中实现超导电性[25],可以预计掺杂浓度较小,这里也考虑低掺杂的情况,选取化学势µ0.4.在计算局域电子态密度的时候,采用 10×10 的超原胞.我们已经通过数值计算进行仔细验证,当参数在实验允许的范围发生合理的变化时,结果定性的行为不发生变化.

3 计算结果和讨论

本文重点讨论石墨烯材料在s 波超导态下的磁性杂质效应,首先根据(7)式的超导序参量的自洽方程,考虑同一个格点上存在有效吸引势V,在Js0.6时,自洽求解得到超导序参量的空间分布.结果展示在图1,其中,序参量的大小用格点的颜色表示,蓝色点是杂质所在位置.

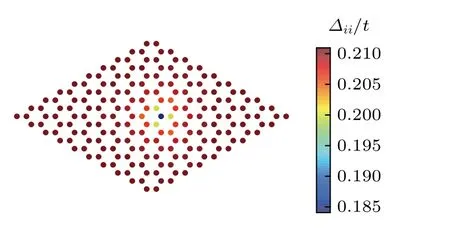
图1 根据(7)式自洽计算得到的s 波超导序参量的空间分布Fig.1.Spatial distribution of the superconducing order parameter based on the self-consistent calculation [Eq.(7)].

如图1 所示,在杂质点附近,超导序参量在一定程度上被压制.序参量在杂质点处达到最小值,在这里,杂质对超导序的压制,主要是由于局域磁矩的影响.通常,超导序和磁性总是互相竞争的关系,局域磁矩的存在一定会压制超导电性.但另一方面,根据自洽结果可以看出,杂质对超导序的影响范围并不大,当格点远离杂质点时,序参量慢慢增加,当格点距杂质点超过两个晶格常数的距离之后,序参量大小恢复为均匀值.因此,可以合理地预期,不需要太大的格点系统就可以得到比较准确的结果.本文通过数值验证了这一点,在考虑的原胞数从 6×6 慢慢增加到 20×20 之后,得到的结果并没有明显差别.

我们进一步研究杂质对粒子数以及局域磁矩的影响,根据(8)式和(9)式,计算了平均粒子数和局域磁矩在实空间的分布,计算结果在图2 展示.对于粒子数和杂质的关系,如图2(a)所示,杂质的存在对粒子数影响很小,整个空间粒子数分布接近均匀(均在1.04—1.05 之间).这是因为在计算中仅仅考虑了杂质带来的磁效应,忽略了杂质的非磁散射项.另一方面,从图2(b)可以看出,在杂质点上,有明显的局域磁矩存在,在杂质最近邻点,局域磁矩急剧减小.在距离更远的地方,局域磁矩消失.众所周知,超导体中局域磁矩的存在可能会导致YSR 态的出现[20-22].但是目前根据局域磁矩在空间的分布,我们可以预期,如果单个磁性杂质确实可以诱导出YSR态,则仅仅在杂质点以及杂质的最近邻点可以看到明显的YSR 共振峰.

图2 (a) 平均粒子数 ni 的空间分布;(b) 局域磁矩 mi 的空间分布Fig.2.(a) Spatial distribution of the on-site particle number ni ;(b) spatial distribution of the local magnetic moment mi.

我们展示磁性杂质附近局域电子态密度的计算结果.首先看s 波配对的情况,图3(a),(b)分别展示了杂质点以及杂质最近邻格点处局域电子态密度和能量之间的关系.在杂质点处,如图3(a)所示,随着杂质项的引入,当Js0.6时,在能隙内,出现了额外的共振峰,随着Js变大,共振峰往费米能处移动,在Js2时,共振峰出现在非常接近费米能的低能位置.此外,研究结果显示,共振峰总是成对出现的,并且出现的能量始终是正负对称的,这是起源于超导体的电子空穴对称性.另一方面,共振峰的强度是正负不对称的.

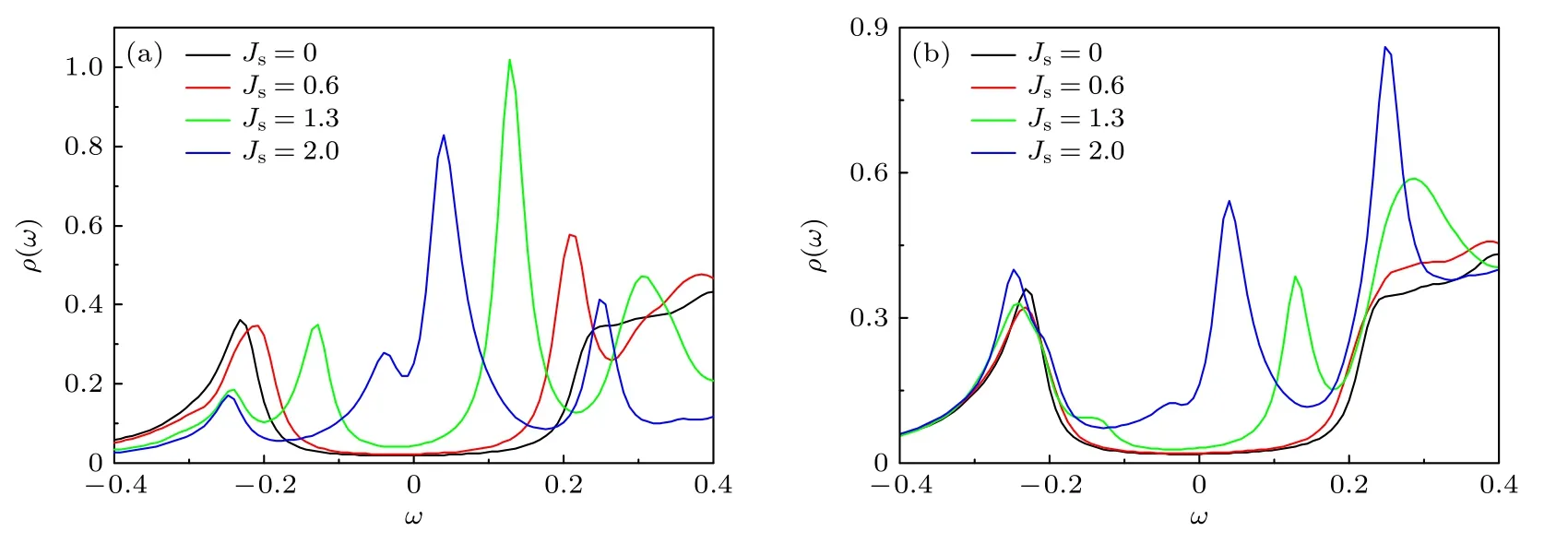
图3 s 波配对情况下磁性杂质附近的局域电子态密度的计算结果(a) 杂质点位置的局域电子态密度;(b) 杂质最近邻格点上的局域电子态密度Fig.3.Numerical results of the local density of states near the magnetic impurity site for the s-wave graphene based superconductor:(a) The local density of states at the impurity site;(b) the local density of states at the nearest neighbor site of the impurity.

在杂质的近邻格点,如图3(b)所示,和杂质点的局域电子态密度类似,当Js0时,出现了明显的能隙内的共振峰.和杂质点上的计算结果相比,共振峰的位置没有发生变化,但是,共振峰的强度明显减小.通过数值验证了在距离杂质更远的格点,共振峰几乎消失,这一结果也与图2(b)所展示的局域磁矩的计算结果一致.以上共振峰的性质符合YSR 态的特性[20-22].最近,实验上在石墨烯超导材料的晶界附近观测到了YSR 态的特征[25],实验结果显示:共振峰的强度具有正负不对称的特性,且共振峰的位置依赖于磁交换作用J的大小,图3 中展示的理论计算结果和实验结果定性一致.

之前,在T-矩阵的基础上,针对石墨烯超导材料的磁性和非磁性杂质效应有过系统的理论研究.有必要将计算结果与T 矩阵的结果进行定性的比较.对于磁性杂质,基于T 矩阵的理论计算显示,在磁性杂质势不是足够强时,不存在能隙内杂质态,能隙内的杂质态仅仅在杂质势超过能带宽度W(石墨烯的能带宽度约为6),杂质态才会出现,并且杂质态的位置和杂质势大小密切相关.在本文计算中,在杂质势J=0.6 的时候,杂质态已经出现,显然,基于BdG 方程方法得到的杂质效应要显著得多.由于BdG 方程是全空间的自洽计算,充分考虑了杂质对序参量的影响,所以分析认为,BdG 方程的计算结果更加接近于实际情况.

进一步研究d+id 和p+ip 配对对称性情况下的磁性杂质效应,考虑最近邻格点之间存在有效吸引势V,根据(8)式自洽计算超导配对序参量,在自洽计算基础上进一步根据(11)式计算局域电子态密度.图4(a)和图4(b)分别展示了d+id配对时,杂质点上和杂质近邻格点的局域电子态密度的计算结果,图4(c)和图4(d)是相应的p+ip 配对对称性时的计算结果.如图所示,对于这两种配对对称性,始终没有YSR 态的出现.本文结果表明,对于单层石墨烯超导体,仅仅在s 波超导态中存在YSR态,这一方面解释了最近的实验结果[25],另一方面,也明确了该实验中石墨烯材料中由于临近效应导致的有效配对是s 波对称.

图4 d+id 波和p+ip 波配对情况下磁性杂质附近的局域电子态密度的计算结果(a) d+id 配对杂质点位置的局域电子态密度;(b) d+id 配对杂质最近邻格点上的局域电子态密度;(c) p+ip 配对杂质点位置的局域电子态密度;(d) p+ip 配对杂质最近邻格点上的局域电子态密度Fig.4.Numerical results of the local density of states near the magnetic impurity site for the d+id-wave and p+ip-wave graphene based superconductor:(a) The local density of states at the impurity site for the d+id pairing symmetry;(b) the local density of states at the nearest neighbor site of the impurity for the d+id pairing symmetry;(c) the local density of states at the impurity site for the p+ip pairing symmetry;(d) the local density of states at the nearest neighbor site of the impurity for the p+ip pairing symmetry.

我们有必要讨论石墨烯超导中磁性杂质效应和非磁性杂质效应的不同.本文主要讨论的是低掺杂浓度的石墨烯超导体,在这一掺杂区域下,对于非磁性杂质,根据之前T 矩阵的理论计算结果[17],当配对对称性为s 波和p+ip 波时,均不存在能隙内的杂质态,当配对对称性为d+id 配对时,非磁性杂质会诱导出能隙内的共振态,但是其性质和磁性杂质诱导的YSR 态具有明显区别.非磁性杂质诱导出来的共振态,共振峰的位置相对比较稳定,随着杂质势的变化仅仅有轻微的移动.

杂质态产生的位置和原因,通常可以根据T矩阵的方法来分析,对于超导体,由于能隙的存在,通常T 矩阵分母的虚部在能隙内会很小,如果在低能量时T 矩阵分母实部也穿过零点,就会出现能隙内的共振态.在过去基于T 矩阵方法对杂质效应的研究中,已经广泛地通过研究T 矩阵分母来讨论杂质态产生的机制[16,17].但是,由于本文是基于BdG 方程的方法研究杂质效应,目前无法进一步给出杂质态产生,以及s 波和其他两种配对对称性磁性杂质效应计算结果不同的物理原因,背后的物理机制需要进一步研究.

4 结论

本文在实空间BdG 方程的基础上,研究了石墨烯超导体的磁性杂质效应.考虑磁性杂质破坏了系统的平移对称性,在平均场的基础上自洽计算了超导序参量.在此基础研究了磁性杂质附近的局域电子态密度计算结果表明,在超导配对是传统的s 波配对时,磁性杂质附近出现了YSR 态.但对于p+ip 配对和d+id 配对,则没有出现任何能隙内的共振态.

针对s 波超导体的理论计算结果和近年来在石墨烯-传统超导体组成的异质结系统中发现的YSR 态的实验结果定性一致.一方面解释了实验现象,另一方面促进了我们对石墨烯类超导体的理解.同时本工作仍然存在一些不足,其中最主要的不足是在BdG 方程的框架下,无法对YSR 态的成因以及产生条件做进一步的理论分析.这是BdG方法研究杂质效应的缺点.我们预期,如果从T 矩阵的角度研究磁性杂质效应,能够解决这一不足,给出能隙内束缚态的成因,并讨论其产生条件,这也是我们下一步研究工作的方向.