失谐整体叶盘多模态振动抑制的吸振器阵列方法1)
王 帅 孙 磊 吴 君 郑召利 付海岭 毕传兴
* (合肥工业大学噪声振动工程研究所,合肥 230009)
† (武汉第二船舶设计研究所热能动力技术重点实验室,武汉 430205)
** (北京理工大学自动化学院,北京 100081)
引言
整体叶盘是新一代高性能航空发动机的关键部件,具有结构紧凑、重量轻和推重比高等优点,代表了高性能航空发动机的发展方向[1].然而,由于缺少了传统叶盘中的干摩擦阻尼,整体叶盘往往具有低阻尼特征,导致其通过共振区域时振幅大.整体叶盘结构模态密集,而航空发动机工况多变、激励频带宽,会激起叶盘多阶模态振动.此外,整体叶盘的制造误差以及服役过程中的不均匀磨损会破坏结构的循环对称性,并引发失谐现象.失谐现象难以避免且随机性强,而整体叶盘对失谐较为敏感,微小的失谐即可引发振动局部化现象,导致部分叶片的振动幅值和应力出现显著增加,并诱发高周疲劳损伤和裂纹故障[2].当前,失谐整体叶盘的振动问题已成为制约高性能航空发动机发展的瓶颈之一[3],整体叶盘的抑振问题也成为国内外研究的热点,得到了众多学者以及NASA,GE,MTU 等知名机构和航空发动机厂商的关注.国内外学者从提升结构阻尼、降低失谐敏感性等角度出发,提出了多种整体叶盘减振方法,包括: 摩擦环阻尼[4-7]、硬涂层阻尼[8-11]、压电阻尼[5,12-15]和主动失谐等[16-20].当前,发展适用于航空发动机整体叶盘的减振技术依然充满挑战,需要同时满足性能高效、结构可靠等多方面严苛要求,要能够有效抑制整体叶盘的多模态共振以及随机失谐引发的振动局部化问题,还要能在航空发动机复杂恶劣环境中长期可靠工作.
动力吸振方法是工程中应用最广的振动控制方法之一,具有性能高效和结构简单可靠等优点,能够以较小的质量实现对复杂结构的高效减振[21-23].近年来,部分学者将动力吸振方法引入整体叶盘减振中.宾夕法尼亚州立大学Sinha[24]采用集中参数模型研究了在叶片上安装有吸振器的整体叶盘的振动特性,分析结果表明叶片上的吸振器能够有效抑制叶盘振动,且在失谐情况下也有很好的效果.但该研究没有给出吸振器的具体实现形式,且该吸振器安装在叶片上,在实际应用中实现难度大.密歇根大学Lupini 等[25-26]在摩擦环阻尼的基础上集成了吸振器的概念,给出了摩擦环阻尼与吸振器的集成设计方案,并针对一个简化叶盘结构进行了仿真分析,展示了良好的减振效果.但研究中所设计的吸振器构型加工制造难度大,且容易因磨损而削弱减振性能.近期,Lupini 等[27]以一悬臂梁叶片为对象,开展了吸振器方法的实验研究,实验结构展示了该方法的良好减振效果.Wang 等[28]提出了一种接触界面法向正压力准确可控的干摩擦阻尼吸振器结构构型,研究了基于吸振器阵列的两阶模态控制方法,并分析了该方法对叶盘两阶模态共振响应的抑制效果,结果表明该方法对失谐整体叶盘两模态抑振效果显著.动力吸振方法为整体叶盘减振问题提供了新途径,现有的研究展示了该方法的优异性能和巨大潜力.当前,面向整体叶盘的动力吸振方法的研究还处于起步阶段,还需在新型吸振器构型、多模态抑振机理以及参数优化等方面开展深入研究,以建立高效、可靠的整体叶盘动力吸振方法.
本文研究面向失谐整体叶盘多模态抑振的吸振器阵列方法,构建整体叶盘-吸振器阵列系统的集中参数模型与功率流分析模型,研究吸振器阵列参数对于整体叶盘多模态振动响应的影响特征,分析吸振器参数随机偏差对其减振性能的影响,并通过实验对吸振器阵列方法的有效性进行验证.
1 吸振器阵列的多模态抑振策略
吸振器阵列结构为集成了多个悬臂梁式吸振器的环形结构,如图1 所示,可以直接安装在轮盘外缘内侧,吸振器阵列结构远离叶盘的流道,不影响叶盘的流场和气动性能.吸振器阵列可以单独制造并安装到叶盘中,对于叶盘的设计与制造流程影响较小.为确保在高速旋转时吸振器阵列与叶盘结构不脱落,可采用过盈配合方式进行安装,确保二者静态和高速旋转时保持紧密贴合.此外,为降低吸振器阵列加工制造的难度,还可将环形吸振器阵列结构分解为两个半环形,分别进行制造,并通过焊接或螺栓连接起来.另外,通过对结构进行合理设计,采用具有较高强度的悬臂梁式振子构型和高强度、耐高温的合金材料进行制造,能够实现在复杂恶劣环境中可靠运行.

图1 吸振器阵列结构及多模态抑振示意图Fig.1 Schematic diagram of the dynamic absorber array and the multimodal vibration suppression scheme
吸振器阵列方法利用动力吸振原理来实现振动抑制,对于共振幅值过大的一阶或多阶模态振型,通过设置与之匹配的吸振器,利用吸振器吸收和耗散结构的部分振动能量,达到提升结构阻尼、降低共振幅值的目的.吸振器阵列中集成的众多吸振器为多模态抑振提供了有效途径,通过采用多组不同的吸振器,分别匹配叶盘的多阶模态,可实现多模态控制.整体叶盘中对失谐较为敏感的模态主要为叶片主导模态与叶片-轮盘耦合模态,结构振动能量主要分布在叶片上,因而对于叶片振动的控制是决定减振性能的关键.虽然吸振器安装在轮盘内侧,远离振动较大的叶片,但由于吸振器的减振作用主要取决于参数匹配程度,通过合理设计吸振器参数,能够有效控制叶片处的振动.
2 整体叶盘-吸振器阵列系统的集中参数建模与功率流分析
整体叶盘是具有循环对称性的复杂结构,在过去几十年中,国内外学者主要采用了集中参数模型和有限元模型对叶盘进行建模和分析.虽然三维有限元模型能够实现高保真建模,但模型自由度大,分析求解难,一般需要与模型缩减方法相结合,以降低计算需求.集中参数模型虽然保真度低,但能够反映谐调与失谐叶盘的主要振动特征,且模型简单、分析求解容易,在失谐叶盘振动机理及减振方法研究中应用广泛.本文探讨吸振器阵列方法的多模态抑振特性,由于吸振器阵列参数众多,而三维有限元模型在进行参数调整时非常繁琐.为此,本文采用如图2所示的集中参数模型表征整体叶盘-吸振器阵列系统的动力学行为.

图2 失谐整体叶盘-吸振器阵列系统的集中参数模型Fig.2 Lumped parameter model of the mistuned blisk-dynamic absorber array system
基于系统的集中参数模型,失谐整体叶盘-吸振器阵列系统的动力学方程可表示为
式中,M为系统质量矩阵,Kb与Ka分别表示叶盘与吸振器贡献的刚度矩阵,Cb与Ca为叶盘与吸振器对应的阻尼矩阵,其中叶盘结构阻尼采用瑞利阻尼进行描述,即Cb=βKb,Kδ表示失谐刚度矩阵.各矩阵的具体形式如下
式中,d iag(·)表示对角矩阵;作用在各叶片上的载荷为具有相位差 φi=2 πC(i-1)/N的简谐力
式中,B与 ω 为激励幅值和频率,C为激励阶次.
通过对式(1)进行求解可得整体叶盘-吸振器阵列系统的振动响应
在现有的叶盘振动特性研究中,主要关注的响应特征为最大振幅.最大振幅包含了多个部件的综合影响,难以直接反映系统振动能量特征.本文采用功率流分析方法[29]量化吸振器阵列对于叶盘振动能量传递与耗散的影响特征,以展示吸振器阵列方法的多模态抑振机理.结构的功率流以一个周期内的瞬时功率的平均值进行量化,即
式中,f(t)与(t)分别为瞬态的力和速度.
根据式(6),可得由输入的平均功率为
轮盘部件耗散的平均功率为阻尼器cc与阻尼器cg耗散功率之和
整体叶盘-吸振器阵列系统中各部件的输入功率与耗散功率随频率变化而变化,反映了不同频率下各部件振动能量的分布与传递特征.
3 吸振器阵列的单模态抑振特性
在系统集中参数模型基础上,研究吸振器阵列对整体叶盘结构的抑振特性.鉴于动力吸振器主要在窄频带中起作用,首先分析吸振器阵列的单模态抑振特性,为多模态吸振器阵列的设计提供基础.本文采用的叶盘集中参数模型参照文献[4],具体为:mb1=0.25 kg,mb2=0.35 kg,md=1.2 kg,kb1=2×106N/m,kb2=1×106N/m,kc=5×107N/m,kg=6×105N/m,B=5 N,β=0.002/ωn,其中 ωn为被控模态的固有频率,阻尼系数cb1,cb2,cc与cg由 β 与对应弹簧刚度确定,叶片的失谐刚度系数
考虑到吸振器阵列中包含了匹配多个模态的多个序列,针对每个吸振器序列定义质量比、频率比和阻尼比等无量纲参数
式中,Na为控制模态数,质量比 µm表征吸振器序列的总质量与叶盘质量的比值,频率比 λm表示吸振器与被控模态的频率匹配情况,阻尼比 ξm反映吸振器的阻尼水平.由于采用的是无量纲参数,分析得到的结论更具一般性和参考价值.
图3 为叶盘固有频率随节径数的变化情况,图中包含了低阶与高阶叶片主导以及叶片-轮盘耦合型模态.为充分展示吸振器阵列方法对于不同类型模态的抑制效果,并考虑各模态对失谐的敏感性,从中选取了3 阶模态振型作为控制对象,并分别简记为TM1,TM2 和TM3,图4 为这3 阶模态的振型图,由图可看出各模态下叶片和轮盘的变形特征.

图3 整体叶盘结构固有频率Fig.3 Natural frequencies of the blisk

图4 整体叶盘结构的模态振型Fig.4 The modal shapes of the integral blisk
TM1,TM2 和TM3 模态在共振频率范围内的功率流特征以及95%振幅放大因子(AMF)变化情况分别如图5 和图6 所示.由功率流变化特征可清晰看出各模态共振时的振动能量分布和耗散特征,其中TM1 和TM3 为叶片主导模态,轮盘耗散的振动能量几乎可忽略,TM2 模态共振时,轮盘耗散了一定的振动能量,且这3 阶模态对于失谐都较为敏感,95%振幅放大因子的最大值均超过1.9.

图5 整体叶盘结构的功率流变化特征Fig.5 The power flow characteristics of the blisk

图6 失谐整体叶盘结构的振动响应统计特征Fig.6 Statistical characteristics of vibration response of mistuned blisk
针对TM1,TM2 和TM3 模态,依次分析吸振器阵列对这3 类模态的抑振特性,结果如图7~图9所示.分析中的质量比为0.01,0.02 与0.03,阻尼比包含0.5%,1%,2%和5%这4 种情形,并对比了吸振器数为8 和24 情形.在各分析情形中,吸振器均具有相同的参数.为量化吸振器阵列的抑振效果,定义减振幅度R为

图7 吸振器阵列对叶盘TM1 模态的减振效果Fig.7 The vibration reduction performance of the dynamic absorber array for the Mode TM1 of blisk

图7 吸振器阵列对叶盘TM1 模态的减振效果 (续)Fig.7 The vibration reduction performance of the dynamic absorber array for the Mode TM1 of blisk (continued)
式中,Aa与Ab分别为添加吸振器与无吸振器叶盘的最大振幅,R越大表示抑振效果越好.
由图7 可知,通过合理设计吸振器,可以使得TM1 模态共振幅值下降70%以上,最优情况下可获得超过80%的减振幅度.吸振器阵列的质量比、阻尼比、频率比和吸振器数量都会对抑振性能产生影响.在质量比和吸振器数量确定的情况下,存在最优频率比和最优阻尼比,减振效果在最优频率比下达到最佳,随着吸振器频率偏离最优频率,减振性能有所下降.吸振器阻尼比的影响也较为显著,虽然小阻尼比情况也能够获得较大的减振幅度,但R-λ 曲线较为尖锐,减振性能对频率调谐误差比较敏感;随着阻尼比的增加,R-λ 曲线逐渐趋于平缓,对于频率比的敏感性下降,但过大的阻尼比也会降低最佳减振幅度.随着质量比由0.01 升至0.03,最大减振幅度有所提升,R-λ 曲线的尖锐度有所下降,因此适度增加质量比可提升减振性能、降低对频率调谐误差的敏感性.当然,过大的质量比也会导致吸振器总质量过大,影响整体叶盘的轻量化,因而选择中等的质量比,可平衡两个方面的需要.对于吸振器数量的影响,在质量比和阻尼比相同的情形下,吸振器个数为24 时的最大减振幅度略大于8 个吸振器的情形.这是由于在吸振器数量较多时,每个扇区均有与之对应的吸振器,而在8 个吸振器情形下,每3 个扇区共享一个吸振器,振动传递距离相对更远,进而影响了总体的减振性能.总体而言,吸振器阵列方法对于TM1模态的抑振性能较好,通过选择合理的吸振器质量比、阻尼比和频率比参数,能够在较大参数范围内获得50%以上的减振幅度,且选择较少数量的吸振器也能获得较好的抑振性能,这一点为多模态抑振提供了良好的基础.
由图8 可知,吸振器阵列对于TM2 模态的抑振效果更好,最大减振幅度超过90%,且在小质量比下也具有较好的效果;各参数情形下的R-λ 曲线均较为平缓,对频率比变化较不敏感.质量比、频率比、阻尼比以及吸振器数量对其减振性能的影响特征与TM1 模态类似,质量比的增加可以提升最优减振幅度,提升阻尼比可降低对于频率比的敏感性,吸振器数量为24 时的减振效果也略好于8 个吸振器情形.吸振器阵列对TM2 模态效果更好的主要原因在于: TM2 模态具有显著的叶片-轮盘耦合,叶片上的振动能量能够有效地通过轮盘传递到吸振器上,使得吸振器吸收和耗散更多的能量.对于类似于TM2模态的叶片-轮盘耦合模态,选择较小的质量比与合适的阻尼比,能够获得较好的减振性能.

图8 吸振器阵列对叶盘TM2 模态的减振效果Fig.8 The vibration reduction performance of the dynamic absorber array for the Mode TM2 of blisk

图8 吸振器阵列对叶盘TM2 模态的减振效果 (续)Fig.8 The vibration reduction performance of the dynamic absorber array for the Mode TM2 of blisk (continued)
图9 为吸振器阵列对于TM3 模态的抑振特性,总体而言,吸振器阵列对于TM3 模态也有较好的抑振效果,只是最优减振幅度略低于TM1 和TM2 模态.在小质量比情形下,最大减振幅度有限,且对频率调谐误差敏感.在大质量比情形下,最大减振幅度可达到70%以上.对于此类模态,可选择较大的质量比和中等的阻尼比,并通过提高加工精度确保频率调谐精度,以获得较好的减振性能.

图9 吸振器阵列对叶盘TM3 模态的减振效果Fig.9 The vibration reduction performance of the dynamic absorber array for the Mode TM3 of blisk
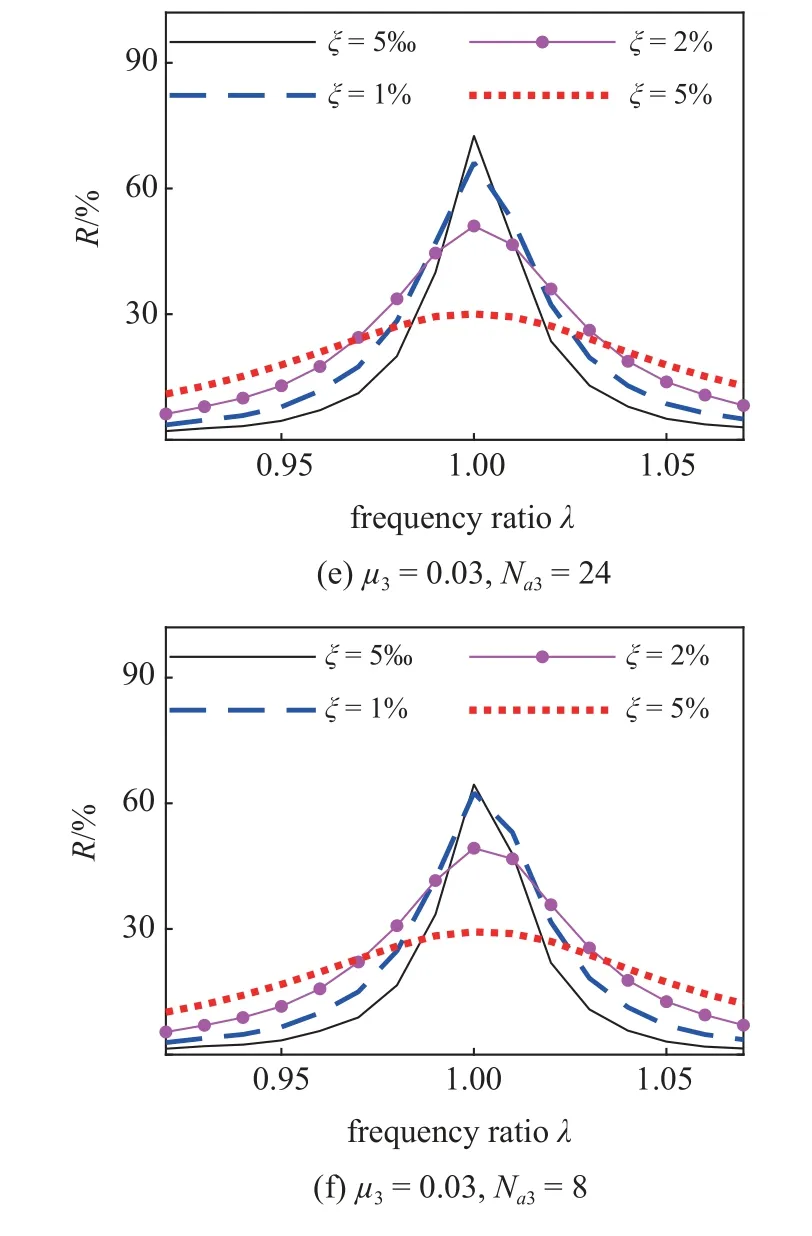
图9 吸振器阵列对叶盘TM3 模态的减振效果 (续)Fig.9 The vibration reduction performance of the dynamic absorber array for the Mode TM3 of blisk (continued)
根据图7~图9 中的结果,可以看出吸振器阵列的减振性能对频率调谐精度最敏感,其次是阻尼比,质量比和吸振器个数的影响相对较弱.在进行吸振器阵列设计时,可首先确定质量比和吸振器个数,进而通过分析选择最优阻尼比和频率比.
4 吸振器阵列的多模态抑振特性
通过对TM1,TM2 和TM3 模态的分析可知,吸振器阵列能够有效抑制叶盘的共振幅值,且对多种不同模态均有较好的效果.本节研究吸振器阵列同时抑制TM1,TM2 和TM3 模态的效果.根据单模态抑振结果,匹配各模态的吸振器数量为Na1=Na2=Na3=8,质量比分别设为 µ1=0.02,µ2=0.01,µ3=0.02,考虑到阻尼比的影响效果以及工程实际中的实现形式,选择 ξ1=ξ2=ξ3=1%.在此基础上,选择吸振器的频率比,由于TM3 模态的固有频率与TM1 和TM2差异大,故频率比 λ3=1.TM1 与TM2 模态的固有频率很接近,二者存在相互影响,采用遍历方式获得较好的频率比组合,结果如图10 所示.由图可知:λ1和 λ2的不同组合对于减振性能的影响明显,综合两者的影响,选择 λ1=0.98,λ2=0.96.

图10 最大振幅比与频率比 λ1 和 λ2 的关系Fig.10 The relationship between amplitude reduction level and the frequency ratio λ1 and λ2
图11 为整体叶盘-吸振器阵列系统在3 阶模态频率范围内的功率流特征,与无吸振器时的结果(图5)对比可知: 吸振器阵列显著降低了叶盘的输入功率,且输入功率的绝大部分被吸振器耗散,叶片与轮盘结构耗散的功率较少,清晰地展示了吸振器阵列方法的作用机理.
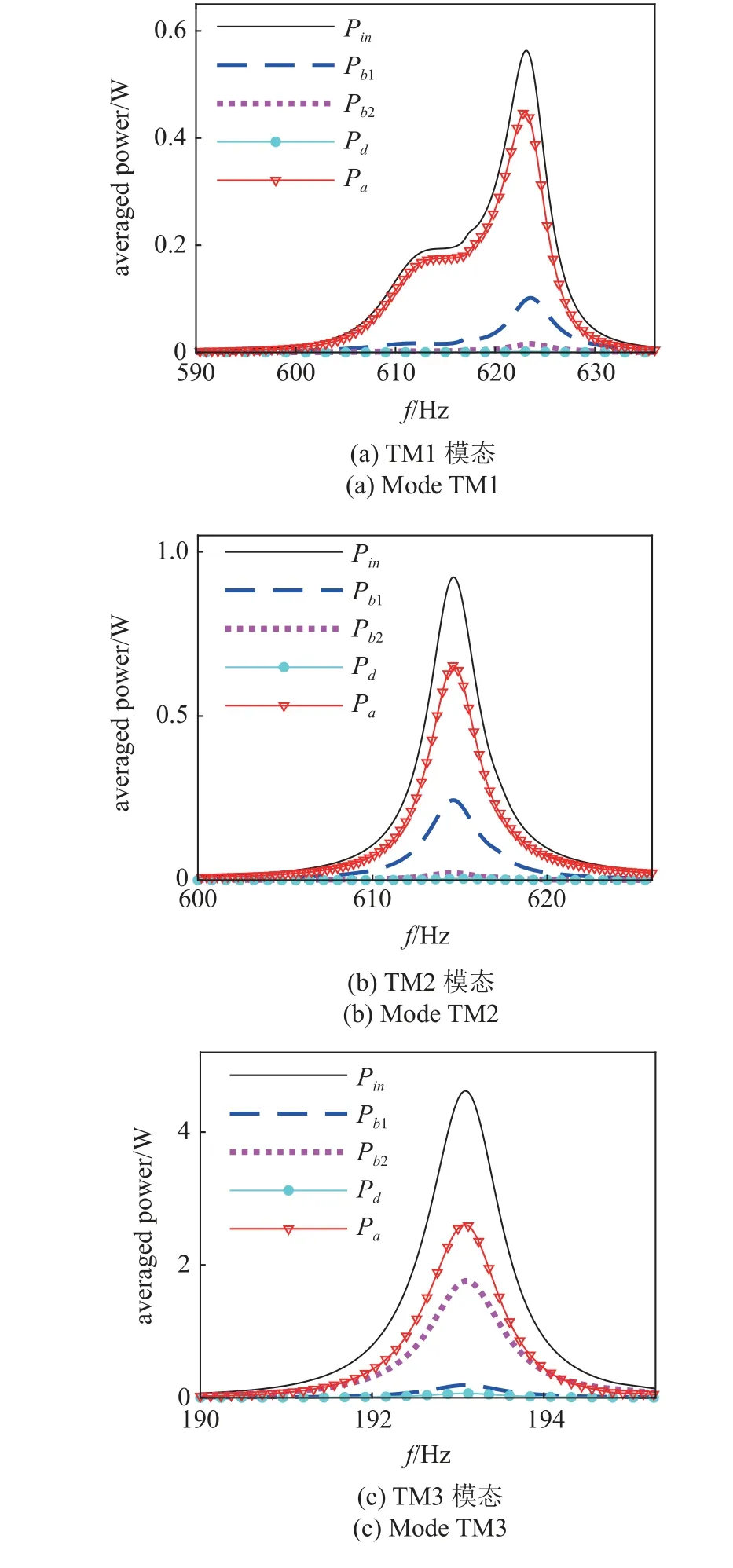
图11 吸振器阵列影响下的叶盘功率流特征Fig.11 The power flow characteristics of the tuned blisk under the influence of the dynamic absorber array
进而,研究吸振器阵列对于失谐叶盘的抑振效果,图12 为安装吸振器阵列的失谐叶盘结构95%振幅放大因子的统计特征,由图可知,吸振器阵列显著降低了失谐导致的振幅放大现象.对于TM1 和TM2 模态,95% 振幅放大因子在很大范围内降至1 以下.对于TM3 模态,95%振幅放大因子下降明显,尤其是在小失谐和中等失谐水平下.此外,1%的阻尼比总体上的效果较好,对于部分模态,适度调整阻尼比可获得更好的抑振性能.

图12 吸振器阵列对失谐叶盘振动响应统计特征的影响Fig.12 Influences of the dynamic absorber array on the statistical characteristics of response of mistuned blisk
前述分析均假设吸振器具有相同的参数,但实际吸振器间不可避免存在一定偏差.为此,分析吸振器参数偏差对其减振性能的影响.由前述分析可知,频率比对吸振器性能影响最显著,因而本文保持各吸振器的质量比和阻尼比不变,通过随机改变吸振器的刚度来模拟随机频率调谐误差情形
式中,δi为随机数,本文采用由均值为0、标准差为σa的正态分布生成随机数序列.
本文取标准差 σa=1%,随机生成了50 组随机偏差序列,并依次带入到失谐叶盘-吸振器阵列系统模型中,开展统计分析,结果如图13 所示,图中粉色区域为50 组95%振幅放大因子的包络区域.由图可知,吸振器阵列参数的偏差会对其减振性能产生影响,且对不同模态的影响程度存在差异,其中对于TM1 和TM2 模态的影响较小,对应的包络区域较窄,而对TM3 模态的影响较大.此外,在不同失谐水平下,吸振器参数偏差的影响也存在差异.在小失谐水平下,如 σ ≤2%,吸振器参数偏差均导致减振性能劣化,即图中粉色区域整体高于无偏差情形.在大失谐水平下,如 σ ≥4%,吸振器参数偏差并非一定降低抑振性能,反而有可能带来一定程度的性能提升,如图中粉色区域的中心线低于无偏差情形.因此,可以主动引入合理的参数偏差,通过牺牲部分小失谐水平下的性能,来显著提升大失谐水平下的性能,以获得更好的总体抑振性能.

图13 吸振器频率比存在随机偏差时的抑振效果Fig.13 The performance of the dynamic absorber array considering parameters deviations
本节分析的多模态吸振器阵列的总质量仅为叶盘的5%,通过合理的参数设计,显著抑制了叶盘的3 阶模态共振响应,减振效果显著.此外,吸振器阵列方法在各吸振器存在小的参数偏差时仍具有较好的抑振性能,鲁棒性较好.
5 吸振器阵列方法的实验验证
为验证吸振器阵列方法的有效性,搭建了如图14 所示的实验台,该实验台主要包括: 简化叶盘、吸振器、压电驱动器、行波激励系统和振动测量系统等.实验台采用简化叶盘作为被控对象,便于加工,能够反映实际叶盘的振动特征;激励系统由基于Labview 的信号发生器生成多组具有相位差的谐波信号,经压电控制器放大,驱动压电片激励叶盘振动;通过设置不同的信号相位差,可产生多种不同阶次的激励信号,激励叶盘不同节径的模态振型;加工了悬臂梁形式的吸振器,并在吸振器上黏贴黏性阻尼材料,吸振器黏贴在叶片根部位置,模拟安装在轮盘外缘内侧的吸振器阵列结构.

图14 吸振器阵列方法原理验证实验台Fig.14 A test bench for the dynamic absorber array approach
如图14 所示的简化叶盘具有12 个叶片,每个叶片的根部黏贴一片压电片,吸振器个数也为12.实验中抑制的模态为一个二节径模态,固有频率为270.96 Hz,吸振器的总质量为叶盘质量的3.15%,吸振器的实测阻尼比为2.21%,实验中观测的是各叶片端部的振动幅值.图15 为安装吸振器阵列前后各叶片端部振动幅值的包络曲线,由于叶盘加工存在一定的偏差,导致该叶盘存在一定程度的失谐,使得叶盘的包络曲线出现两个共振峰.在安装了吸振器以后,叶盘共振峰显著降低,共振峰出现了分裂现象,最大振幅由 1.59×10-4m 降为2.36×10-5m,减振幅度达到85.2%.实验结果展示了吸振器阵列方法对于叶盘减振的优异效果.

图15 安装吸振器阵列前后各叶片端部振动幅值的包络曲线Fig.15 The envelopes of the vibration amplitudes of the tips of blades with and without the dynamic absorber array
5 结论
(1)本文提出了基于多组吸振器的失谐整体叶盘多模态抑振方法,通过集中参数模型和功率流分析方法,揭示了吸振器阵列对于谐调与失谐整体叶盘多模态振动的抑制机理.分析结果表明: 吸振器阵列方法可以有效抑制叶片主导与叶片-轮盘耦合型模态,也能够以较小的附加质量同时抑制多阶模态共振,对失谐导致的振幅放大现象控制效果显著.
(2)吸振器阵列的减振性能与质量比、频率比和阻尼比等参数紧密相关.一般而言,增加质量比能够提升最优减振性能,并降低对于吸振器频率调谐误差的敏感度.在一定质量比下,存在最优频率比和阻尼比,过小或过大的阻尼比都不利于吸振器吸收和耗散振动能量,通过合理设置质量比和阻尼比,可在较大频率比范围内获得较好的减振性能.
(3)吸振器阵列方法的减振性能对于吸振器加工制造误差具有较好的鲁棒性,还有可能通过合理的吸振器频率主动偏离设计获得更好的综合性能.本文的研究结果对于发展高效、可靠的整体叶盘多模态抑振方法具有重要的参考价值.

