五轴数控机床后置处理算法研究及其验证

王洪申，朱佳钰，朱家亮

（兰州理工大学 机电工程学院，兰州 730050）

0 引言

复杂曲面被广泛的应用于航空航天、化工、能源、工具等多个领域[1]。五轴数控加工是实现复杂曲面高效率高精度加工的重要方法。五轴数控机床是在三个平动轴的基础上增加了两个转动轴，这样不仅可以使刀具相对于工件的位置任意变动，而且刀具的轴线相对工件的方向实时改变。五轴数控机床增加的两个旋转轴，则工件坐标系下的刀路轨迹与机床坐标系下的数控程序之间是非线性的，机床坐标系下的旋转轴存在着不同的可行解[2-4]。

五轴数控机床编程可分为两步完成，首先在工件坐标系下，对刀具的运动轨迹进行规划，生成刀具轨迹规划文件（刀位文件）。刀位轨迹规划产生的刀位信息没有考虑具体的机床结构和数控系统类型，无法直接应用于数控机床加工，需要进行后处理。后置处理技术是数控编程技术的关键技术之一，数控编程的后处理就是通过机床运动学的变换将刀位数据转变成机床可以识别的数控加工程序描述机床各个轴的运动，操控机床加工运动[5]。后处理的开发流程大概为：首先选择机床的类型与后处理类型，设置运动轴参数与刀轨参数，设置自定义参数，最后检测所设置的参数是否合格。机床的后置处理研究就是针对不同机床开发不同的后处理软件，通过对机床特点的研究和机床坐标系和CAM加工坐标系之间关系的研究，建立其对应的运动模型，可将刀位文件转化为机床可以直接识别的数据[6]。在刀位文件后处理中，不同机床的运动形式与数控加工中的各种坐标系间的变换非常重要[7]。目前文献中所建立的运动模型缺少数据对比，不能证明所建立模型的正确性。文中对三种类型的五轴数控加工机床建立对应的数学模型，并阐述了运动原理。为验证所得数学模型的正确性，使用UG NX软件进行建模仿真，使用文中数学模型计算所得出数据与软件生成的数据进行对比。所得数据与生成数据对比结果完全吻合。

1 机床运动变换模型

五轴数控机床可以根据旋转轴相对于工件和刀具的不同配置，可以分配为双转台式[8-9]、转台摆头式[10]和双摆头式[11～13]三种类型。图1为三种不同机床结构的示意图。

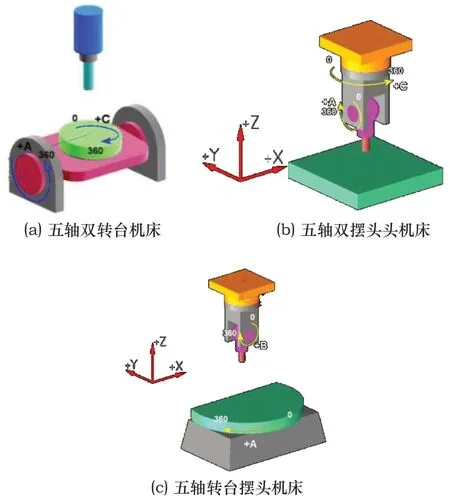
图1 三种不同种类机床

1.1 五轴双转台机床运动转换

五轴双转台机床两个旋转轴都作用于工件。在描述数控机床的运动时，采用右手直角坐标系：平行于主轴的坐标轴定义为z轴，绕x、y、z轴的旋转坐标分别为A、B、C。该类型的机床运动加工时，X、Y方向的平动由工作台实现，Z方向的平动由主轴带动刀具实现。机床床身上工作台可以环绕x轴回转，定义为A轴，A轴工作台一般能进行的摆动，在摆动台上还设有一个回转台，绕z轴回转，定义为C轴，一般可进行360°的旋转。通过A轴C轴组合，可完成在工作台上除底面之外的五个面的加工。这种结构的优势是主轴结构非常的简单，主轴刚度较好，生产的成本比较低，适合加工中小型工件。与机床直接相连的为定轴，与定轴相连的为动轴。按照定轴、动轴的顺序分为A-C、A-B、B-A、B-C四种类型。图2为A-C结构五轴双转台机床坐标系定义和运动链构成示意图。五轴双转台机床A轴为定轴，C轴为动轴。其中OMXMYMZM（MCS）为与机身固联的坐标系，在机床的运动中，此坐标系在运动中保持不变。刀轴方位矢量在MCS中始终保持不变。OWXWYWZW(WCS)为工件坐标系，工件固定在工作台上，WCS随着工作台的运动而运动。OTXTYTZT为刀具坐标系，绕A轴旋转的坐标系为OAXAYAZA，绕C轴旋转的坐标系为OcXCYCZC。OAXAYAZA是与定轴A轴固联的坐标系，OcXCYCZC是与动轴C轴固联的坐标系。设当前刀位点位置（x,y,z）和刀位矢量为（i,j,k）。绕X轴旋转角度设为A，绕Z轴旋转角度为C。变换后坐标为（X,Y,Z）。机床先进行X、Y、Z轴的平动，再进行A、C旋转轴的转动[14-15]。

在机床运动学变换中绕X轴旋转某一转角变换矩阵如下：

在机床运动学变换中绕Z轴旋转某一转角变换矩阵如下：

OcXCYCZC与初始OAXAYAZA的相对位置的矩阵如下：

当机床运动到某个点，OAXAYAZA与初始OcXCYCZC的相对位置的矩阵如下：

1.2 五轴双摆头机床运动转换

五轴双摆头机床两个旋转轴都作用在刀具上。这类机床的主要特点是依靠主轴头的旋转带动刀具旋转完成加工，其前端是一个回转头，能够带动刀轴绕Z（C）轴进行360°的旋转。回转头上还有一个可以带动刀轴环绕X轴进行旋转的A轴，一般可以进行±90°以内的回转。C轴与A轴轴线的交点称为主轴支点，主轴支点只完成X与Z方向的平动，刀具的运动是随着主轴支点的平动和旋转运动的组合来完成的。工作台的运动只有Y方向的平动。这种结构的优点是主轴加工非常灵活，工作台也可以设计的非常大，适用于具有多曲面的零件的加工或者大型零件的加工。按照定轴、动轴的顺序分为C-A、C-B、B-A、A-B种类型。图3为五轴双转头机床坐标系定义。其中旋转轴C轴为定轴，旋转轴A轴为动轴。其中OMXMYMZM（MCS）为与机身固联的坐标系，在加工过程中，MCS固定不动。OWXWYWZW（WCS）为工件坐标系，WCS随着工作台的平动而移动。OTXTYTZT为刀具坐标系。OcXCYCZC是与定轴C轴固联的坐标系，OAXAYAZA是与动轴A轴固联的坐标系。设当前刀位点位置（x,y,z）和刀位矢量为（i,j,k）。绕X轴旋转角度设为A，绕Z轴旋转角度为C。变换后坐标为（X,Y,Z），L为枢轴距离（C轴零点到端面的距离），坐标为（0,0,L）。机床先进行X、Y、Z轴的平动，进行C轴定轴旋转，最后进行A轴定轴旋转。

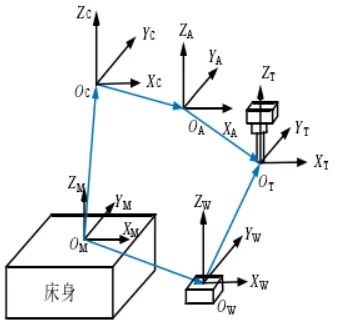
图3 机床坐标系定义

工件绕X轴旋转的A角度的变换矩阵为：

工件绕Z轴旋转C角度的变换矩阵为：

OcXCYCZC与初始OAXAYAZA的相对位置的矩阵如下：

当机床运动到某个点，OAXAYAZA与初始OcXCYCZC的相对位置的矩阵如下：

1.3 五轴转台摆头机床运动转换

五轴转台摆头机床一个旋转轴作用于刀具上，另一个旋转轴作用于工件上。该类型的机床运动加工时，Y方向的平动由工作台实现，X、Z方向的平动由主轴带动刀具实现。工作过程中，工件固定在工作台上，适合加工工件体积大，重量重的工件，但主轴的刚度比较差，加工的切削量比较小。按照定轴、动轴的顺序分为B’-A、A’-B、A’-C、B’-C四种类型（带’的轴为刀具摆动）。图4为B’-A结构五轴转台摆头机床坐标系定义。五轴转台摆头B’-A机床旋转轴B轴作用于刀具，旋转轴A轴作用于工作台，带动工件运动。其中OMXMYMZM为与机身固联的坐标系，OWXWYWZW为工件坐标系，OTXTYTZT为刀具坐标系。设当前刀位点位置（x,y,z）和刀位矢量为（i,j,k）。绕X轴旋转角度设为A，绕Y轴旋转角度为B。变换后坐标为（X,Y,Z）。转台摆头机床是床身和机头分开进行运动。先进行平行运动再进行旋转运动。

图4 机床坐标系定义

工件绕X轴旋转的A角度的变换矩阵为：

工件绕Y轴旋转的B角度的变换矩阵为：

变换后的矩阵为：

OwXwYwZw与OAXAYAZA的相对位置的矩阵如下：

OmXmYmZm与OBXBYBZB的相对位置的矩阵如下：

2 利用UG NX软件绘制模型验证算法正确性

以上论述了数控机床通用机床运动变换模型的建立和求解方法，任何方法都必须经过实践检验才能判断其正确与否。建立五轴待加工模型曲面进行五轴加工，通过UG NX软件加工仿真生成刀具轨迹如图5所示。利用UG NX软件的仿真加工生成CLSF文件，通过后置处理生成NC文件。将生成的NC文件数据与CLSF文件使用算法计算的生成的坐标点和角度点进行对比，并列出表格对比上述两组数据对应的坐标点和角度的值，验证算法的正确性和合理性。为简化计算，设机床旋转轴的轴线相交。

图5 验证模型

首先任取表1五组CLSF数据：

表1 5组CLSF数据

CLSF文件经过后处理得到NC文件，为验证上述算法的正确性，截取与CLSF相对应的五组NC数据。表2为双转台机床5组数据信息验证对比，表3为双摆头机床5组数据信息验证对比，表4为摆头转台机床5组数据信息验证对比。表中NC1是通过UG NX仿真加工得到的数据，计算为通过本文使用公式所推导出来的数据。A、B、C角度表示数据为NC文件时，刀轴在加工过程中所移动的角度。表1中的i、j、k向量为在CLSF文件中刀轴矢量在平面坐标系中的投影。在UG NX软件中坐标点默认的有效位数为0.0001，投影向量的有效位数为0.0000001，角度的有效位数为0.001。

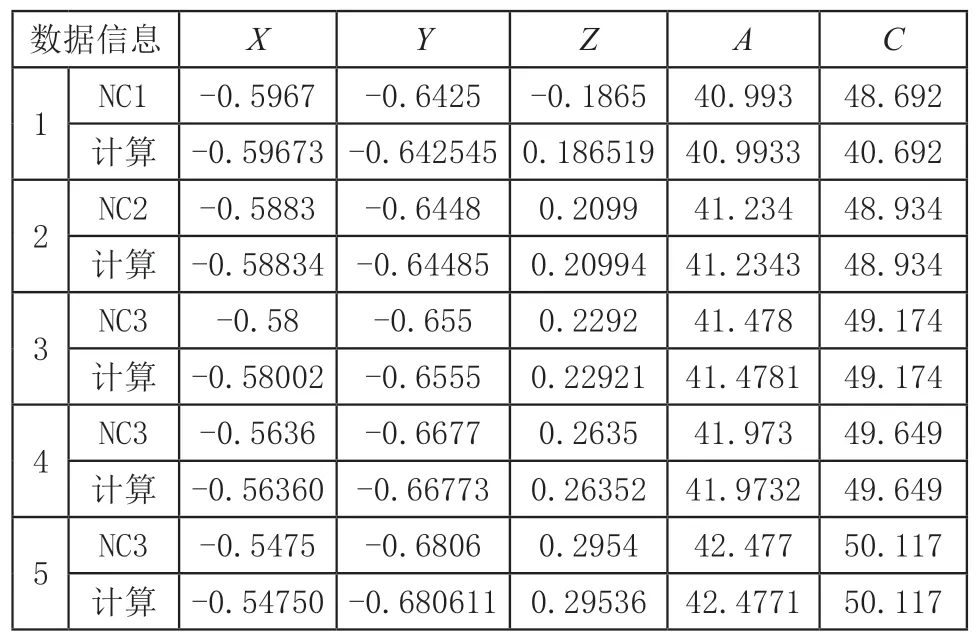
表2 双转台机床5组数据信息验证对比

表3 双摆头机床5组数据信息验证对比

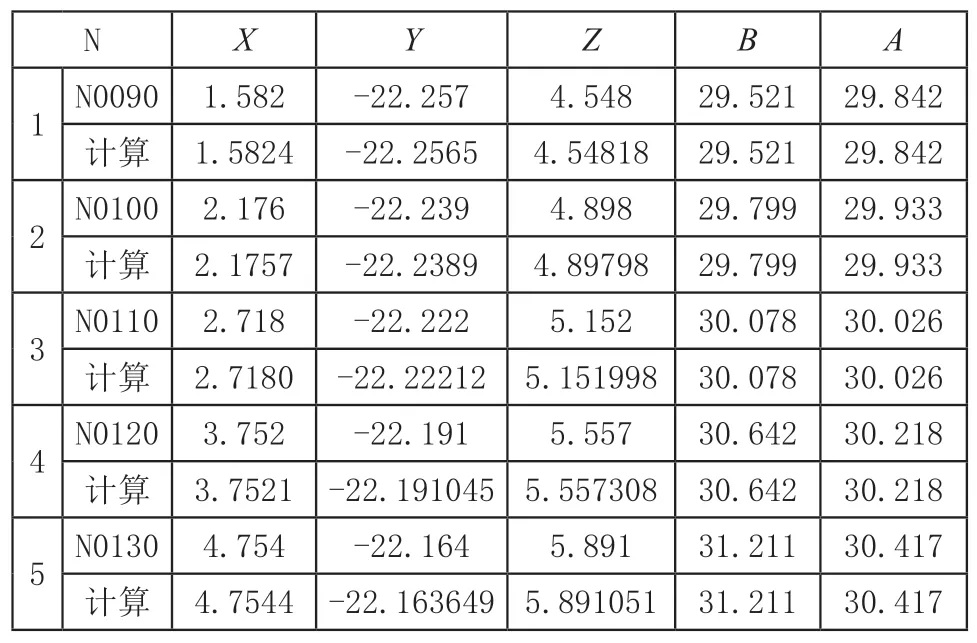
表4.摆头转台机床5组数据信息验证对比

通过表2、3、4的数据对比，验证了上述推导算法的正确性，满足了理论与实际的需要。

3 结语

本文通过对五轴数控机床的三种类型的结构特点进行具体的运动分析，建立了数学模型推导出各类机床的后置处理算法。并通过UG NX进行建模并进行后处理与算法得到的后处理数据进行对比，证明了文中算法的正确性。通过所推导的数学公式得知，坐标的角度变换与转台的转动相关。所推导的数学模型为最基础的数学模型，可以在此基础上进行模型的变化，来适用多种工况。