多元线性回归在主泵对中的应用
杜 川
(辽宁红沿河核电有限公司,辽宁 大连 116319)
0 引言
联轴器联接主泵与电机轴,使二者同步旋转并传递一定扭矩。泵轴与电机轴的中心线会不可避免的存在相对误差。误差过大会增加泵组运行时的振动,还会增加轴承负荷而导致寿命降低或损坏[1]。因此对中是转动设备检修、安装中不可或缺的重要工作。对中是通过调整泵转子与电机转子的相对位置,使未连接的转子中心在同一轴线上。对中有端面偏差、中心偏差两个控制标准。端面偏差衡量泵与电机联轴器节端面的张角,若消除端面偏差,两联轴节端面将相互平行。中心偏差衡量泵与电机联轴器中心轴线的相对位置,需要在端面偏差调整合格之后进行。若消除中心偏差,泵与电机中心轴线将相互重合[2]。
大多数泵组对中采用三表找正法,4个测量点均匀分布在联轴器外圆。工作人员盘动联轴器,测量百分表在各点的径向值、端面值,从而计算轴系的中心偏差与端面偏差,其示意图见图1。之后可通过在电机地脚增加垫片、调整电机顶丝的方式使得泵组对中合格。各电机地脚增加垫片的厚度及顶丝调整量有成熟的理论计算方法[3]。

图1 端面偏差与中心偏差示意图
主泵电机支架与电机通过螺栓连接。可通过在电机与电机支架之间增加垫片,使得电机联轴节与中间短节的端面相互平行。电机与电机支架之间安装有方向相互垂直的顶丝,通过调整顶丝位移量可使得电机联轴节中心轴线相对于泵联轴节中心轴线移动,使二者重合。目前尚无关于主泵对中过程中,偏差计算及调整的理论方法。本文建立主泵泵组对中的数学模型,通过多元线性回归给出端面偏差与中心偏差的计算及调整方法。
1 端面偏差测量及调整
1.1 端面偏差测量
如图2所示,将中间短节与电机联轴节外圆8等分,通过塞入量块测量泵联轴节与中间短节在各等分点的端面间隙zi。若任意互成180°的两点zi值之差的绝对值≤0.025 mm,则可认为端面偏差合格,否则需进行调整。

图2 端面偏差测量示意图
1.2 端面偏差测量数学模型
端面偏差调整过程可做以下假设,联轴节端面为平面圆,其中心轴线与端面垂直。以中间短节端面为基准面(xoy),中心为原点,建立空间三维坐标系(xyz)。其中①-⑤方向为x轴,③-⑦方向为y轴,中间短节的轴线为z轴。
电机联轴节外圆8个等分点在该坐标系下的坐标为(xi,yi,zi)。zi为1.1中的测量值,xi,yi表达式见式(1),式中r为电机联轴节半径。
(1)
电机联轴器节端面所在平面可表示为:
z=Ax+By+C
(2)
根据模型假设,电机联轴节端面可当作平面,各等分点(xi,yi,zi)应位于同一平面内。由于随机误差的存在,各等分点的坐标并不位于同一平面内。因此可通过多元线性回归的方法找到一个平面,使得该平面与电机联轴节外圆8个等分点距离的平方和最小。求解矩阵方程组(3),可得A,B,C的具体数值。
(3)
1.3 端面偏差调整
电机与支架通过24个均匀分布的螺栓连接,螺栓中心在基准面(xoy)投影的坐标(xk,yk)。表达式见式(4),式中R为电机支架螺栓中心分布圆半径。
(4)
将(xk,yk)代入式(2)中,可得zk。zk为电机支架螺栓在上述建立的三维坐标系下的高度值。在各连接螺栓中心处增加厚度为hk的垫片,即可调整端面偏差,表达式见式(5)。
(5)
2 中心偏差测量及调整
2.1 中心偏差测量
按图3安装百分表。表座安装在中间短节柱面,百分表头与电机联轴节柱面接触,将百分表调零。依次记录百分表在电机联轴节8个等分点处的读数zj。
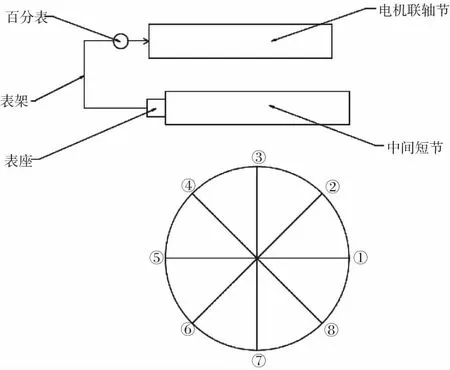
图3 中心偏差测量示意图
任意互成180°的两点百分表读数之差的一半即为电机轴线相对于泵轴线在该方向的偏移分量dj,如表1所示。若任意方向的偏移分量≤0.025 mm,则中心偏差合格,否则需要调整。

表1 轴线在各方向偏移分量的测量值
2.2 中心偏差测量数学模型
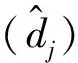

(6)
其中,(xj,yj)为各个方向的单位向量,如表2所示。

表2 各方向单位向量
由于随机误差等因素,各方向轴线偏移的理论值与测量值存在偏差。因此可通过多元线性回归的方法,得到电机轴线坐标(A,B),使各个方向偏移分量的理论值与测量值之差的平方和最小。求解矩阵方程组(7),可得A,B具体数值。
(7)
2.3 中心偏差调整
电机与电机支架安装有方向相互垂直的顶丝。调整x轴、y轴方向顶丝,调节量分别为A、B,可使得电机轴线相对于泵轴线移动,即可调整中心偏差。
3 实例
在某次大修中,其中一台主泵对中时端面偏差测量数据如表3。
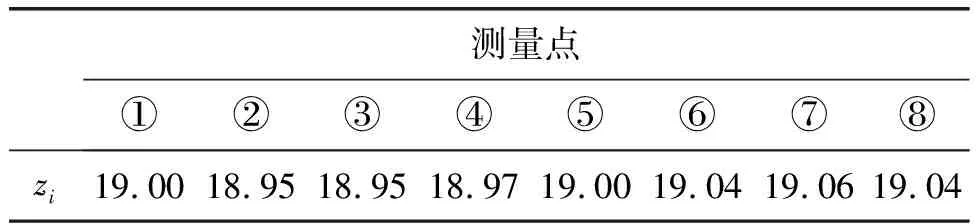
表3 端面偏差测量数据(mm)

表4 各螺栓中心所加垫片厚度
从数据直观来看,③-⑦方向的高度差最大,⑦方向为整个电机联轴节端面的最高点,③方向为最低点。但实际端面的最高点不一定位于所测量点。根据多元线性回归的方法,通过8个等分点的坐标值,可得到电机平面的表达式,可准确得到电机联轴节端面最高点所在的方向为266.4°,最大端面偏差为0.111 mm。且可得到各螺栓中心处添加垫片的厚度值hk。
经增加垫片后复测最大端面偏差为0.015 mm,端面偏差调整合格。中心偏差测量数据如表5。

表5 中心偏差测量数据(mm)
从数据直观来看,③-⑦方向中心偏差最大,为0.215 mm。通过多元线性回归的方法,统筹考虑各个方向偏移分量的测量值,可得到电机轴线的坐标(-0.006 mm,-0.2136 mm)。经调整相应方向的顶丝后,复测中心偏差最大为0.005 mm,中心偏差调整合格。
4 结论
本文建立了主泵对中过程中的端面偏差和中心偏差数学模型。通过8个点的测量值及多元线性回归的方法,给出调整端面偏差和中心偏差的理论方法,填补了工程实践中关于主泵对中理论计算的空白,为现场对中工作指明了方向。本方法计算过程复杂,为方便现场工作人员计算,作者编写了专用的计算软件。经验证,可应用于实际的对中计算工作,提高现场工作效率,同时降低工作组所受的辐射剂量。

