台基噪声功率谱估计中的Welch参数选择
尹康达 李小军 张晓刚 丁 成
1)中国邢台 054000 河北红山巨厚沉积与地震灾害国家野外科学观测研究站
2)中国石家庄 050021 河北省地震局
0 引言
地震台站噪声水平是影响观测数据质量的重要因素(林彬华等,2020),功率谱密度(power spectral density,简称PSD)是研究台基噪声并对其进行量化的重要手段(McNamara et al,2009;葛洪魁等,2013;杨千里等,2019)。噪声的频段范围分布较广,长周期的自然界噪声和高频段的人类活动是地震观测中的主要噪声源(葛洪魁等,2013;谢江涛等,2021);可靠的台基噪声功率谱估计方法可为地震观测环境等级划分、观测数据可用性评估、地震监测能力评估、噪声源分析提取等提供依据。
地震预警系统是基于P 波初始记录进行计算的。预警台站数量的迅速增加对观测数据质量提出了更高的要求(Enferadi et al,2021)。台基噪声功率谱估计及RMS 计算已成为地震台网的日常工作。Welch 修正周期图法(Welch,1967)是计算噪声PSD 的常用方法,但对其参数的选择目前尚无统一标准,这导致计算结果存在较大偏差(Li et al,2015;Xu et al,2019)。Li 等(2015)对Welch 方法中几个常用参数,如窗口函数、窗口长度、分段数据长度、重叠率等的选取进行了研究,发现不同参数组合对PSD 的计算结果会产生较大影响。本研究在此基础上,进一步开展工作,以期对规范日常台基噪声计算中的参数选择提供参考。
1 方法
1.1 功率谱估计方法
通常用PSD 来描述噪声的频域特性,评价一个地震台站的观测等级。利用Welch 方法进行傅里叶变换的数据较短,在许多情况下Welch 方法比其他方法计算量更少(Welch,1967),是目前进行功率谱估计的通用方法(Xu et al,2019)。该方法假设原始数据为一个二阶稳态随机序列,并将其分成若干长度相等的数据段,对分段数据进行加窗重叠,并通过修正周期图来进行谱的平滑和方差的减小,从而在一定程度上减小谱估计的误差。通常窗口长度与分段数据长度相等,文中统一称为窗口长度。Welch方法数据分段示意图如图1 所示。
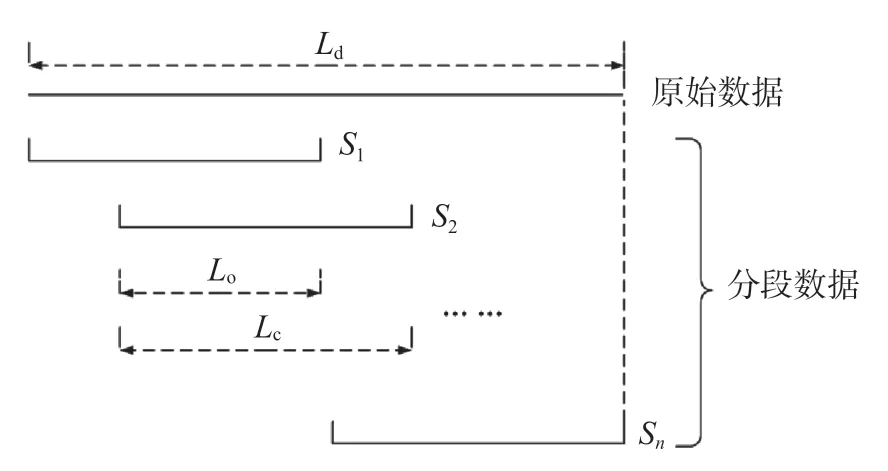
图1 Welch 方法数据分段示意图Ld 为原始数据长度;S1,S2,…,Sn 为分段数据;窗口长度为Lc;重叠部分长度为Lo;重叠率Ro=Lo/LcFig.1 Record segmentation of Welch method
Welch(1967)在进行功率谱估计方法研究时,将方差作为一个重要衡量指标,从理论角度推导出了通过分段和重叠可在一定程度上减小方差,并从计算耗时角度指出,当窗口长度小于原始数据长度的平方根时,耗时更短。本文对重叠率的选择进行了研究,研究结果可对该方法进行一定的补充。
1.2 最低重叠率、匹配重叠率
窗口长度和重叠率取值组合不同,功率谱估计结果亦不同。本文从分段数据匹配的角度,研究窗口长度与重叠率间的关系。
窗口长度占比(本文简称为窗口长度)Rcd=Lc/Ld,当Rcd>50%且重叠率较小时,第2 段数据末端会超出原始数据,从而导致该数据段不参与计算。当第2 段数据末端与原始数据重合时(图2),将对应的重叠率定义为最低重叠率Rom,计算公式为
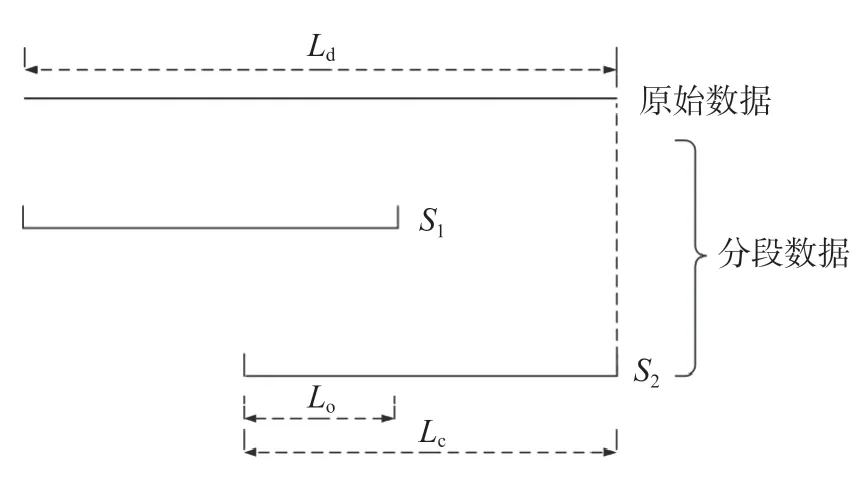
图2 最低重叠率示意图Ld 为原始数据长度;S1,S2,…,Sn 为分段数据;窗口长度为Lc;重叠部分长度为Lo;重叠率Ro=Lo/LcFig.2 Illustration of minimum overlap rate
当窗口长度固定时,仅当Sn末端与原始数据重合时,各段叠加之后的数据才是完整的(图1),将此时的重叠率定义为匹配重叠率Rm;当Ro≠Rm时(图3),Ln+1末端会超出范围,无法参与计算,使得叠加后无法完整覆盖原始数据,造成长度为Ls的数据缺失。
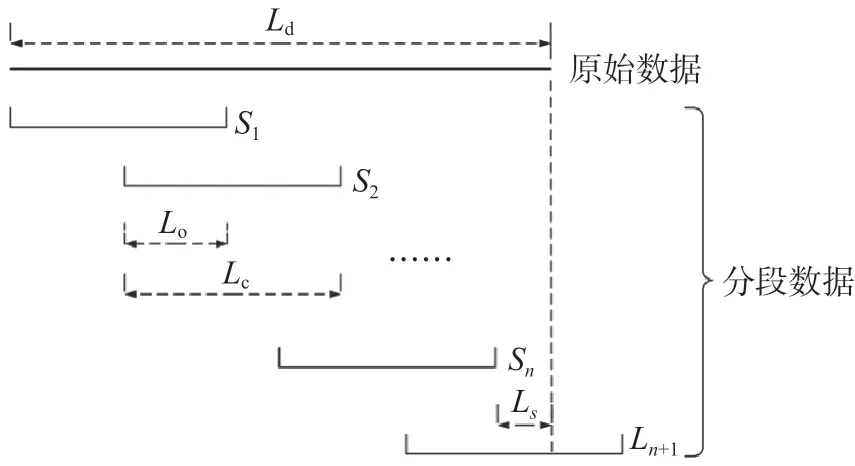
图3 非匹配重叠示意图Ld 为原始数据长度;S1,S2,…,Sn 为分段数据;窗口长度为Lc;重叠部分长度为Lo;重叠率Ro=Lo/LcFig.3 Illustration of unmatching overlap
匹配重叠率计算过程如下:
能够参与计算的有效分段数为
当n≥2 且为整数时,对应的重叠率Ro即为匹配重叠率Rm,公式为
当n=2 时,即最低重叠率;当n=2,3,…,1 000 时,匹配重叠率随窗口长度的变化曲线如图4 所示。当选择其下方区域的参数组合时,仅第1 段数据参与计算,造成数据缺失。最低重叠率曲线可作为对Li 等(2015)提出的K 线的解释。

图4 匹配重叠率随窗口长度的变化红色曲线即最低重叠率Fig.4 Curves of matching overlap rate with window length
1.3 平滑度评价指标
通过周期图法计算PSD 时,对有限长数据的周期性拓展会产生较大的随机偏差,功率谱密度曲线波动较大,平滑度较低,Welch 方法可在一定程度上改善功率谱密度曲线的平滑度。参考Welch(1967)的评价指标,通过方差来表征谱曲线的平滑度,方差计算公式如下
其中,var 为PSD 曲线方差;D为原始数据采样点数;pi为各频点下的PSD 值;pa为各频点PSD 均值。
2 数据处理和分析
宽频带地震计具有较小的自噪声和较大的动态范围(Sleeman et al,2006;李小军等,2019),是目前地震台网常用观测设备之一。选取CTS-1 型甚宽频带地震计进行观测实验,由于甚宽频带地震计对温度变化较敏感(田文德等,2013),传感器安装在山洞内。选取1 h观测数据(采样率为100Hz)进行功率谱估计实验。通过改变窗口长度和重叠率,来研究其对PSD 平滑度的影响,从而确定窗口长度和重叠率的合理取值区间。
数据处理基于MATLAB 软件平台的Pwelch 函数对记录的垂直分量进行计算。由于线性趋势会抵消低频段的频谱能量,使谱估计产生较大失真(Mcnamara et al,2004),因此,在进行功率谱计算之前,对所有记录数据进行去均值和线性趋势处理。
通过方差对功率谱密度曲线的平滑度进行定量分析。窗口长度为1%—100%,步长1%;重叠率为0—99%,步长1%,对10 000 种窗口长度和重叠率的组合,进行功率谱估计实验。
按式(4)计算10 000 条速度功率谱密度曲线的方差,研究不同参数组合对平滑度的影响,计算结果如图5 所示。由图5 可见,方差随重叠率和窗口长度呈阶跃式变化,突变的位置可以形成一系列曲线与图4匹配重叠率曲线相对应。
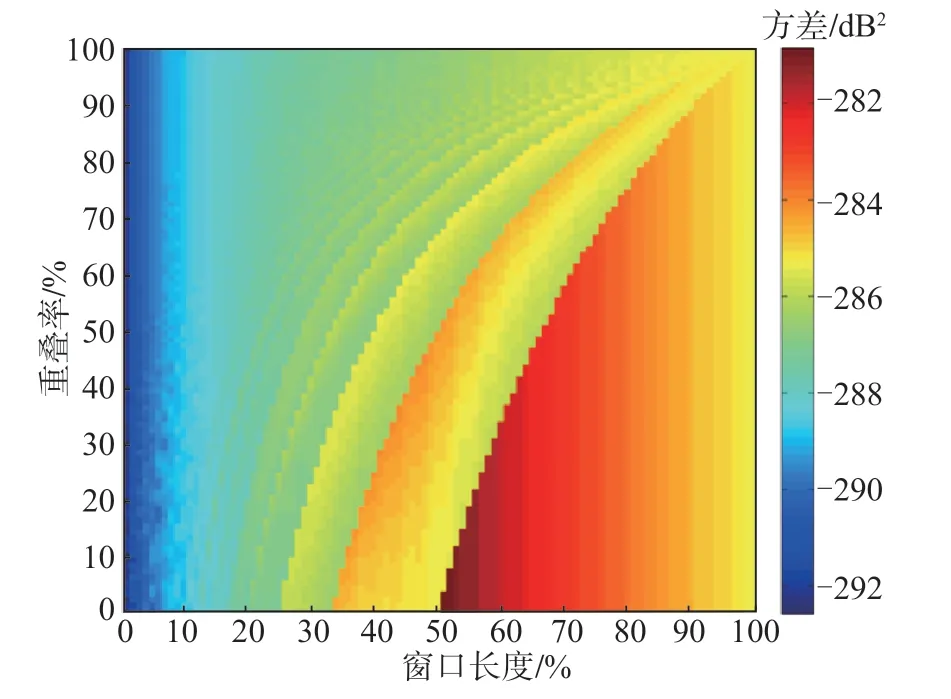
图5 速度PSD 方差随Welch 参数的变化Fig.5 Variance of velocity PSD at different Welch parameters
随着窗口长度的增加,方差呈趋势性增大,这主要是因为未互相重叠的分段数减少,减弱了利用分段平均进行平滑的效果,虽然通过较大的重叠率,可使分段数增加,但重叠部分的平均对平滑度的改善效果不显著。
当窗口长度大于50%时,在最低重叠率下方区域方差整体偏大。由于此时没有通过取均值进行平滑的过程,且与原始数据偏差较大,此区域内方差不随重叠率而改变,为不可靠区域。
当固定窗口长度时,在2 个匹配重叠率间隔内,随着重叠率的增大,方差逐渐增大,这主要是因为窗口叠加之后不能完全覆盖原始数据。对于可近似为随机信号的台基噪声,随着缺失数据的增多,方差变大,谱估计的误差增大;当取匹配重叠率时,方差突然减小,因为此时窗口经过叠加对原始数据形成了全覆盖,功率谱估计相对准确,这也验证了选取匹配重叠率的重要性。同时,对于同一窗口长度取不同的匹配重叠率时,方差变化不大,因为重叠的主要作用是补偿由加窗所造成的信号两端衰减。在同一窗口长度下,增大重叠率,虽然在保证分辨率不降低的前提下,增加了分段数,但多为重复数据,取平均对功率谱密度曲线平滑度的改善效果不明显。
3 结论与讨论
针对台基噪声功率谱估计中的参数选择问题,通过对Welch 方法不同参数组合下功率谱密度曲线的平滑度进行分析,并以方差指标来进行定量研究,可为地震台站观测环境综合评价和观测数据质量分析提供参考。
在本研究中定义了最低重叠率,当窗口长度大于原始数据的50%,重叠率取值小于最低重叠率时,功率谱估计结果不可靠;定义了匹配重叠率,特定窗口长度对应一系列匹配重叠率,且在匹配重叠率下的台基噪声功率谱估计结果更准确。
Welch 方法将原始数据进行分段时,分段长度和重叠率取值都是单一的,这导致重叠率的选取受到限制。在2 个匹配重叠率之间,随着重叠率的增大,缺失数据也会增加,而且当分段数较少时,2 个匹配重叠率的间隔较大,此时若想通过增加重叠率对功率谱估计结果有所改善,必须进行跨越式增大,这将会使计算量大大增加。
因此,如何根据研究目的和原始数据特征,选择更合理的分段、重叠方式,并通过分段加权进行平均,需要开展进一步研究。

