融合正逆程特征的GRU 神经网络关节迟滞特性建模研究＊

党选举 张一晨

（①桂林电子科技大学电子工程与自动化学院,广西 桂林 541004；广西智能综合自动化高校重点实验室,广西 桂林 541004）

传统工业机器人在诸多领域得到广泛的应用，但是在3C、医疗和无人零售等需要柔性作业的场景中，传统工业机器人无法满足特殊的工作要求，因此，轻型工业机器人应运而生[1]。为了满足在未知环境中工作的安全性，在轻型工业机器人中引入柔性，但柔性关节执行器表现出的复杂迟滞特性，严重影响了关节的动态性能和传动精度[2]。因此，除采用高精度制造技术外，迟滞特性的高精度建模是通过补偿控制提高轻型工业机器人传动精度的重要途径之一。

轻型工业机器人关节迟滞特性产生的原因复杂，关节柔性[3]、非线性摩擦[4]、齿轮背隙[5]和装配误差[6]等都会使关节产生复杂的迟滞特性。文献[7]使用广义Maxwell 模型、Preisach 模型和多项式方法对关节中的非线性摩擦和间隙进行综合建模。但模型对非对称的复杂迟滞特性没有适用性。文献[8]在Bouc-Wen 模型的基础上增加了一个具有方向性的修正项，解决了由摩擦导致的能量损失的不确定性。但预测精度受到参数辨识算法的影响，需要在精度和计算复杂度之间做出权衡。柔性关节迟滞特性受到很多因素的影响表现出高度非线性，基于迟滞经典建模方法很难应对所有影响因素。

基于数据驱动的建模方法通过研究系统的相关数据，能够获取其中的规律。机器学习算法具有强大的非线性映射能力和泛化能力，可以学习到数据中的抽象规律，已成为主流的数据驱动方法[9]，并在迟滞建模领域得到应用[10]。文献[11]使用简单动态迟滞算子（SDHO）来描述不同频率下的迟滞特性，并将该算子与混沌神经网络组成串联结构，通过实验验证了模型优于PI 算子与混沌神经网络的串联结构。文献[12]在证明对角递归神经网络（dRNN）特定条件下具有与Preisach 相同的迟滞特性[13]的基础上，提出了一种新的损失函数以保证dRNN 的每个神经元在训练过程中都参与迟滞特性的建模。文献[14]使用有记忆性的VSM 对迟滞特性进行建模，并通过WNN 提取Volterra 核。该模型利用VSM 的记忆性简化了对神经网络输入空间的扩展，并且有效描述迟滞特性的频率相关性。可见，基于数据驱动的整体建模方法可以有效描述由多种因素引起的复杂迟滞特性。

直接将神经网络运用到迟滞建模中无法准确描述迟滞特性，文献[15]提出一种多分支BP 神经网络模型可以有效避免神经网络迟滞建模过程中的过拟合现象。文献[16]在循环神经网络的基础上，将迟滞模型分成了迟滞子模型和频率子模型，使模型能够准确描述迟滞特性的频率相关性。上述文献在建模过程中没有直接考虑迟滞所表现出的多值对应和极值点特性（非光滑特征），通过间接方式考虑迟滞相关特性，设计的结构复杂的迟滞模型，不利于工程应用。

机器人关节迟滞特性建模需要依赖多种传感器的支持，文献[17]构建了关节输出角度与关节输出转矩之间的迟滞非线性关系，用于描述不同刚度下的关节输出转矩。文献[18]针对机器人关节中表现的迟滞特性，构建了磁流变离合器中电流与转矩之间的迟滞非线性特性，并提出了一种转矩补偿算法，提高了柔性关节的控制精度。上述文献中的关节迟滞特性建模方法，以机器人关节配置转矩传感器为前提，不适用于未配置负载转矩传感器的低成本轻型工业机器人柔性关节迟滞特性建模。

本文针对低成本轻型工业机器人柔性关节迟滞特性建模，构建了一种融合正逆程特征的GRU 神经网络迟滞模型。关节执行器未安装负载转矩传感器而无法采用转矩-扭转角之间的关系描述关节迟滞非线性，本文采用电机驱动电流-扭转角，间接描述关节迟滞特性。通过数据驱动的建模方法，利用基于卡尔曼滤波的电流增量，提取正程和逆程的特征，并与GRU 神经网络相融合，构建了一种融合正、逆程特征的GRU 神经网络迟滞模型。将历史预测信息作为模型输入构建动态GRU 神经网络迟滞模型，其结构简洁，具有较高的模型精度。

1 GRU 神经网络迟滞模型

轻型工业机器人柔性关节执行器的迟滞特性是指关节执行器在往复运动中，输出转矩与关节扭转角之间表现出的多值对应关系。这种多值对应关系受到历史输入信号的极大值或极小值的影响，具有记忆性。所以，具有一定的记忆能力的神经网络模型，适合于对迟滞特性的建模。

1.1 门控循环单元

门控循环单元（gate recurrent unit，GRU）[19]是为了解决时间序列长期记忆问题所提出的结构，其特有的重置门和更新门可以对历史数据记忆或遗忘，可以避免迟滞建模过程中扩展输入空间。相较于RNN，GRU 在处理长时间序列问题时，具有更长的记忆且不容易发生梯度爆炸或梯度消失。GRU具有的门结构较LSTM 更少，可以用较少的计算量达到与LSTM 相同的效果[20]。

GRU 单元结构如图1 所示，每个GRU 单元具有2 个门结构，更新门zj(k)和重置门rj(k)，以及1个隐藏状态h˜j(k)，共同决定了GRU 单元的记忆能力。

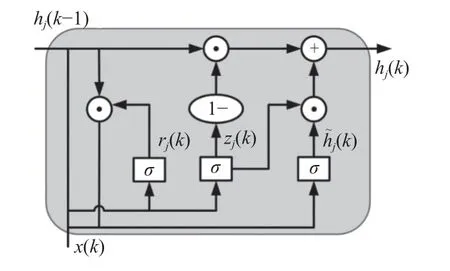
图1 GRU 单元结构图

输入信号x(k)∈Rm，表示k时刻的m个输入信号，GRU 单元的数学表达见式（1）～式（4）。

更新门：

式中：zj(k)表示k时刻更新门的输出值，h(k-1)表示k-1时刻n个GRU 单元的输出值构成的n维向量，即h(k)=(h1(k),h2(k),···,hj(k),···,hn(k))T，其中Wz∈Rn×m和Uz∈Rn×n表示更新门的权值矩阵，表示更新门的偏置量，σ表示sigmoid 函数，(·)j表示第j个元素。

重置门：

式中：rj(k)表示k时刻第j个GRU 单元的重置门的输出值，Wr∈Rn×m和Ur∈Rn×n表示重置门的权值矩阵，表示重置门的偏置量。

隐藏状态：

GRU 单元输出：

式中：hj(k)表示k时刻第j个GRU 单元的输出值。

1.2 GRU 神经网络迟滞模型的构建

图2 是单输入单输出的GRU 神经网络（GRUNN）迟滞模型结构图。将n个GRU 单元的输出值加权求和组成GRU 神经网络迟滞模型的输出层：

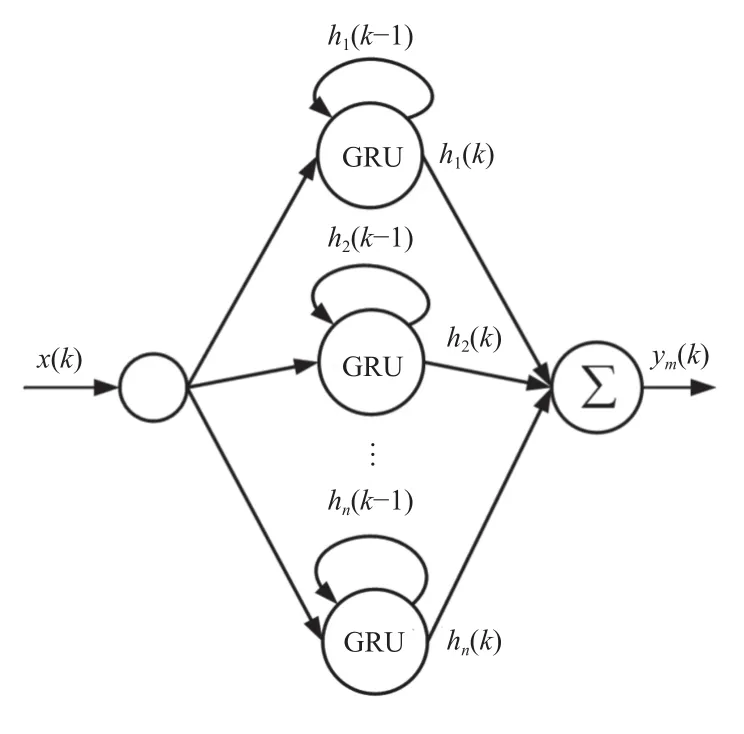
图2 GRU 神经网络迟滞模型结构图

式中：ym(k)表示k时刻GRU 神经网络迟滞模型输出层的输出值，Wy∈Rn表示输出层的权值。

使用沿时间反向传播算法对权值进行更新，其损失函数：

式中：E(k)表示k时刻的损失函数值，yd(k)表示k时刻的目标值，E表示训练数据总的损失函数值。

GRU 神经网络迟滞模型的记忆能力有利于解决迟滞特性对历史输入信号的依赖，因此本文以GRU 神经网络迟滞模型为基础，进一步考虑迟滞特性正、逆程及极值信息，将关节特有的迟滞特征融入其中，成为柔性关节迟滞特性高精度建模的关键。

2 融合正逆程特征的GRU 神经网络迟滞模型

2.1 柔性关节迟滞特征分析

结合图3 和图4 对迟滞特性所具有的多值特性和极值点的特征进行分析。图3 中箭头表示迟滞特性随着时间增加而变化的趋势，输入信号随时间增加而增加称为迟滞特性的正程，输入信号随时间增加而减小称为迟滞特性的逆程。其中，位于正程的p1点和位于逆程的p2点的输入信号大小相等，均为x1，输出信号却对应2 个不同的值，分别是y1和y2。迟滞特性在相同的输入值x1下对应不同输出值y1和y2的情况，被称为多值对应。

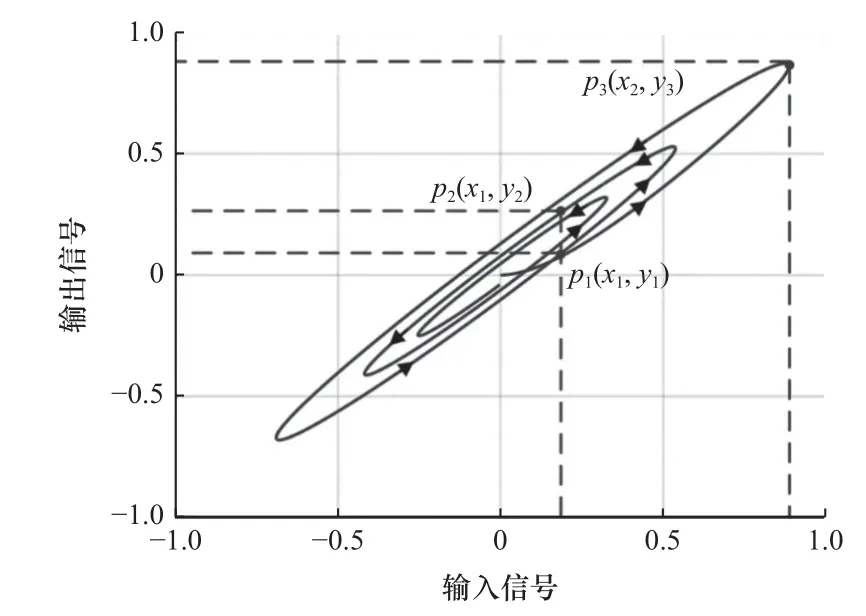
图3 迟滞特性多值对应示意图

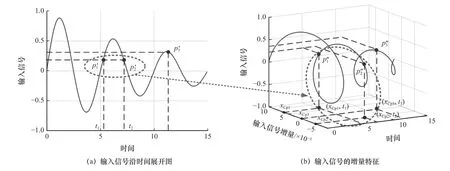
图4 输入信号增量作为正逆程特征

2.1.1 多值对应的特征提取

利用输入信号的增量作为区分迟滞特性输入信号正程和逆程不同变化趋势的特征。将不同时间下相同的输入信号通过不同的增量加以区别，并作为输入信号的特征输入神经网络。

2.1.2 极值点的非光滑性特征弱化

在迟滞特性曲线的转折点，将图3 中的p3点作为迟滞特性的极值点，通常是建模误差较大的位置。通过输入信号的增量特征将p3点对应到图4b 中点，输入信号的增量特征在同一周期的正程和逆程中，极大值点是由输入信号的正增量逐渐变化到零，而极小值点是由输入信号的负增量逐渐变化到零，通过增量的正负区分迟滞特性曲线中的极大值和极小值不同变化趋势，连续变化的增量减缓了极值点处的非光滑性，使极点趋于可导。

2.2 正逆程特征的提取

未安装负载转矩传感器的低成本机器人柔性关节执行器无法使用转矩与扭转角之间的关系描述关节迟滞特性。考虑到电机驱动电流随负载对应变化的特性，本文选取关节电机驱动电流与扭转角之间的迟滞特性作为建模数据，间接描述负载变化导致的柔性关节迟滞特性。

电流传感器采样得到电机驱动电流包含测量带来的干扰信息。为了提取机器人柔性关节电流与扭转角之间迟滞特性的正、逆程特征，需要将实际采样的输入电流信号进行预处理。

式中：KF(·)表示卡尔曼滤波，滤波后的值为xf(k)。将滤波后的残差信号(x(k)-xf(k))进行频域分析可得，电流传感器采样到的信号x(k)包含高斯白噪声，使得神经网络很难稳定到期望输出，导致建模精度下降。数据预处理结果如图5 所示，卡尔曼滤波可以有效滤除输入电流信号中的高斯白噪声。为了从输入电流信号中获得清晰的增量特征，需要对滤波后的结果进行处理。

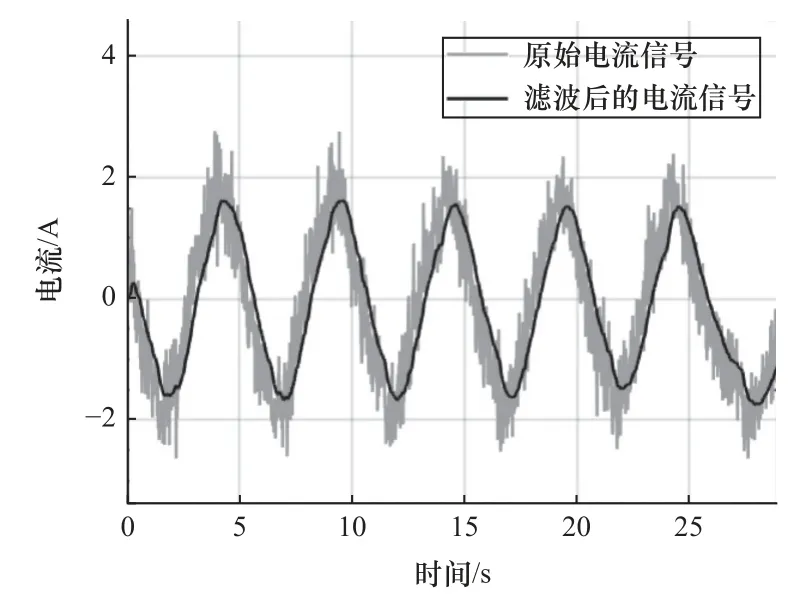
图5 实际采集电流数据的预处理结果

式中：xff(k)表示第二次卡尔曼滤波后的结果，式（9）表示对xff(k)求增量，结果表示为∆xff(k)。为了从输入电流信号中获得清晰的增量特征，将xf(k)再次通过卡尔曼滤波进行处理。如图6 所示，第二次卡尔曼滤波处理前后信号增量特征的变化对比可得，第二次卡尔曼滤波很好地平缓了xf(k)中增量特征的波动。但计算信号的增量会放大高频干扰，引入不必要的噪声，需要进一步对增量特征∆xff(k)处理。

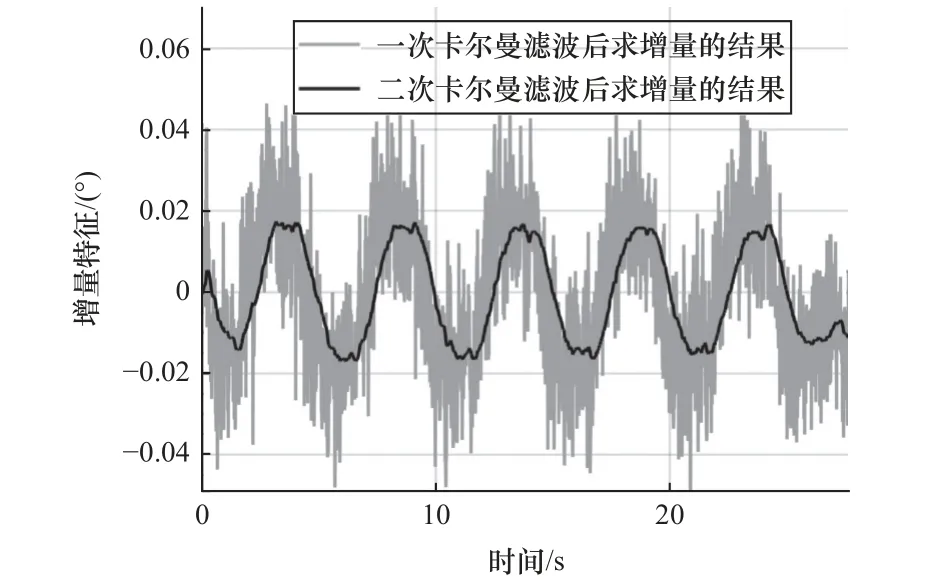
图6 第二次卡尔曼滤波前后增量的变化对比图

式中：xc(k)表示具有迟滞正、逆程特征信息的增量特征。使用xff(k)的增量∆xff(k)描述输入信号在迟滞正程和逆程不同的变化趋势，并将∆xff(k)使用卡尔曼滤波进行处理。卡尔曼滤波可以有效滤除计算增量带来的高频噪声，处理结果如图7 深色曲线所示，得到的xc(k)作为描述迟滞正、逆程变化的特征输入神经网络。

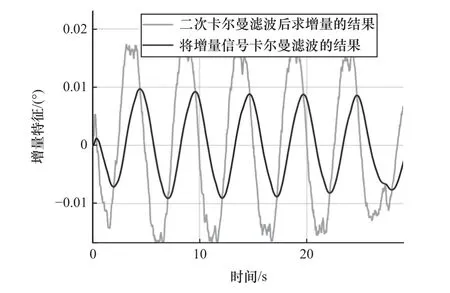
图7 增量信号卡尔曼滤波前后对比图

2.3 融合正逆程特征的GRU 神经网络迟滞模型的构建

融合正、逆程特征提取的GRU 神经网络迟滞模型的整体框图如图8 所示，其中正、逆程特征提取如图8 虚线框所示。

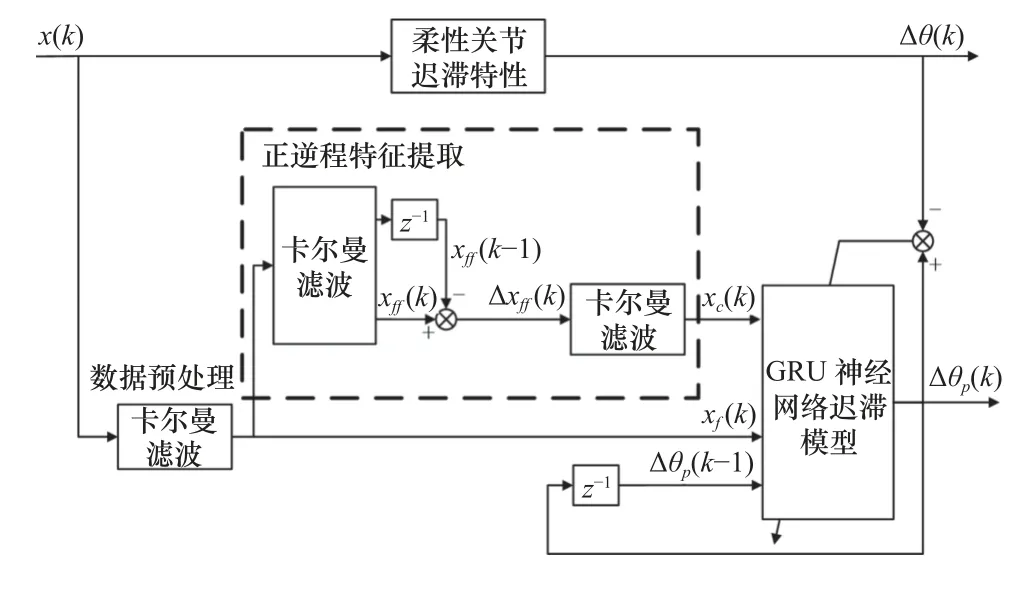
图8 融合正逆程特征的GRU 神经网络迟滞模型框图

所提出的迟滞模型有3 个输入信号，分别是：

（1）正、逆程特征的输入信号xc(k)，其作用是提取输入电流信号在正程和逆程中不同的变化趋势。

（2）数据预处理后的电流信号xf(k)，其作用是将去除掉高斯白噪声的电流信号输入GRU 神经网络。

（3）将GRU 神经网络迟滞模型的扭转角预测结果∆θp(k)的历史值∆θp(k-1)作为神经网络的输入，构建动态的GRU 神经网络迟滞模型。在GRU 神经网络迟滞模型中，融入了柔性关节迟滞特性特有的多值特性和极值点非光滑特性，这个实现是提高关节迟滞特性的高精度建模的关键。

3 实验结果与分析

3.1 实验验证

所搭建的轻型工业机器人GLUON 实验平台如图9 所示。为了保证用于关节迟滞建模的数据具有代表性，选择机械臂第二关节（ID：2）从零位（如图9 中机械臂的位姿）开始进行往复运动，并以100 Hz 左右的采集频率对建模所需的电流信号和扭转角信号进行记录。

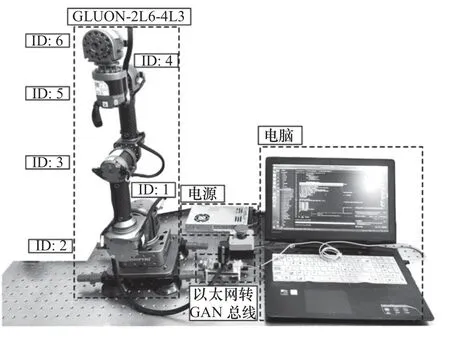
图9 GLUON 实验平台

实验比较了2 种模型的预测结果，GRU 神经网络迟滞模型（图2）和融合正、逆程特征的GRU 神经网络迟滞模型。

两种模型中GRU 神经网络的结构相同，使用20 个GRU 单元作为神经网络隐藏层节点，使用相同的训练数据分别训练。由于机器人关节在大角度周期运动过程中可选择的频率范围并不大，所以使用不同的运动周期去代替描述频率的不同。使用周期为5 s、8 s、10 s 的正弦衰减信号作为机器人关节运动的激励信号，并采集关节往复运动中电流和扭转角作为训练数据。两种模型使用相同的数据训练完成后，分别对6 s、9 s、13 s 的数据进行预测，对比预测结果。

3.2 不同频率下的迟滞模型预测结果

用于提取不同周期预测数据的机器人关节的运动轨迹分别为周期6 s、9 s、13 s 的正弦衰减信号，以验证模型对不同频率且带有次环的关节迟滞特性的预测效果。

机器人关节在周期为6 s 的正弦衰减运动轨迹下，采集到的迟滞数据如图10 中实线所示。GRU神经网络迟滞模型的预测结果如图10a 中虚线所示，对应预测均方误差和最大误差分别为2.16 和3.74 °。融合正、逆程特征的GRU 神经网络迟滞模型的预测结果如图10b 中虚线所示，其预测均方误差和最大误差分别为0.07 和1.05 °。图11 和图12 分别为预测结果的时域展开对比和误差对比图。

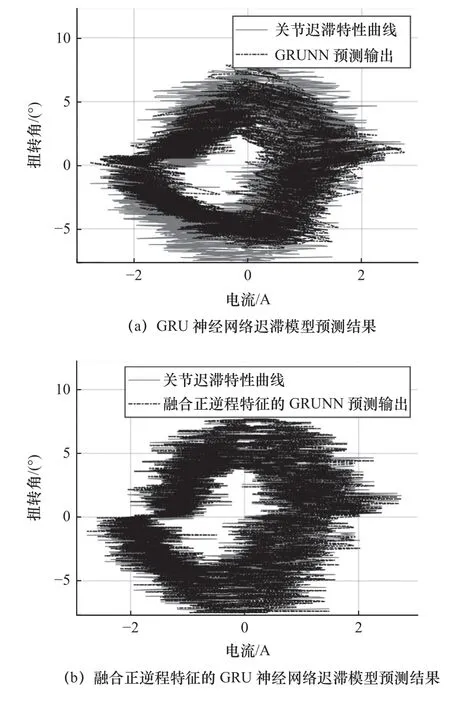
图10 周期为6 s 的迟滞特性预测结果对比图

图11 周期为6 s 的迟滞特性预测输出的时域展开对比图

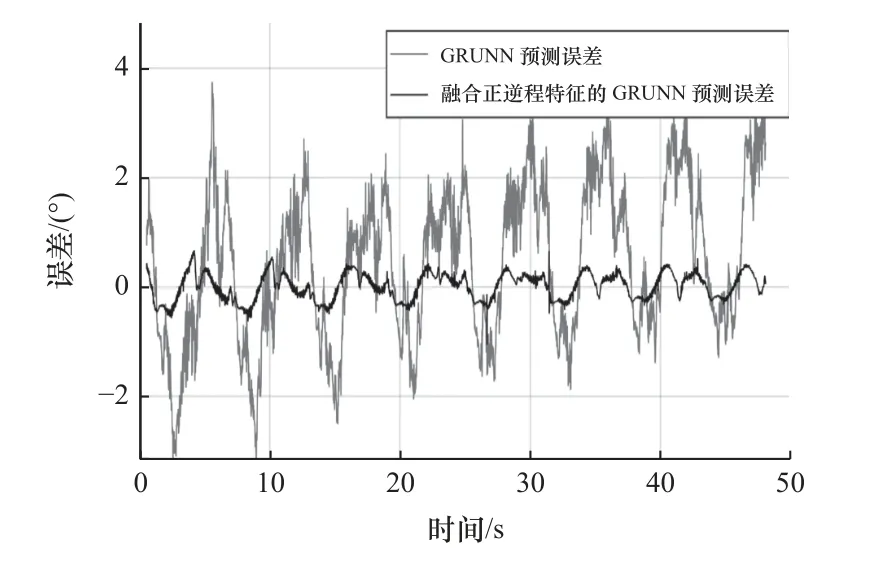
图12 周期为6 s 的迟滞特性预测误差对比图

机器人关节在周期为9 s 的正弦衰减运动轨迹下采集到的迟滞数据如图13 所示，其中，GRU 神经网络迟滞模型的预测结果如图13a 中虚线所示，预测均方误差和最大误差分别为0.66 和2.63 °。融合正、逆程特征的GRU 神经网络迟滞模型的预测结果如图13b 中虚线所示，预测均方误差和最大误差分别为0.01 和0.53 °。图14 和图15 分别为预测结果的时域展开对比和误差对比图，融合正、逆程特征的GRU 神经网络迟滞模型的预测误差更小。

图13 周期为9 s 的迟滞特性预测结果对比图

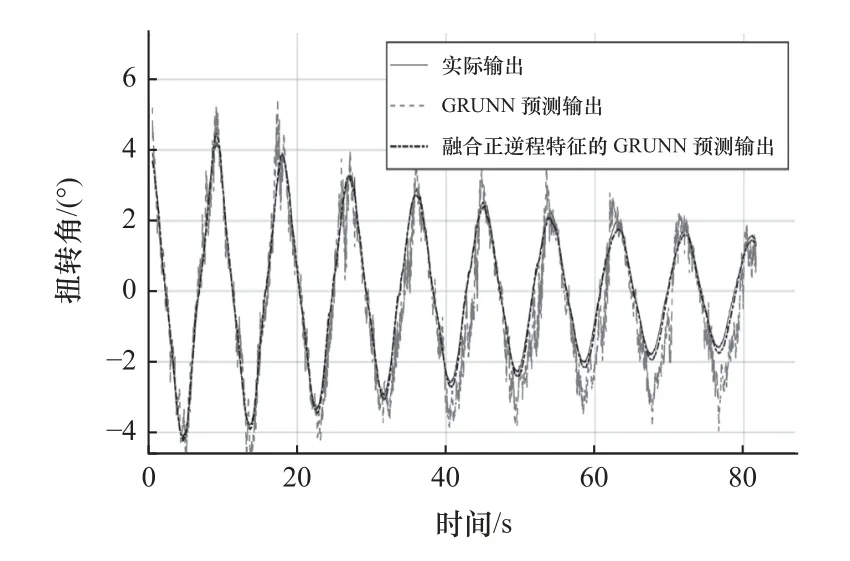
图14 周期为9 s 的迟滞特性预测输出的时域展开对比图

图15 周期为9 s 的迟滞特性预测误差对比图

机器人关节在周期为13 s 的正弦衰减轨迹运动下采集到的迟滞数据如图16 中实线所示，图16a中虚线所示是GRU 神经网络迟滞模型的预测结果，其预测均方误差和最大误差分别为0.93 和4.23 °。融合正、逆程特征的GRU 神经网络迟滞模型的预测结果如图16b 中虚线所示，预测均方误差和最大误差分别为0.01 和0.40 °。图17 和图18 分别为预测结果的时域展开对比和误差对比图。从图中误差对比可知，融合正、逆程特征的GRU 神经网络迟滞模型预测误差明显降低。

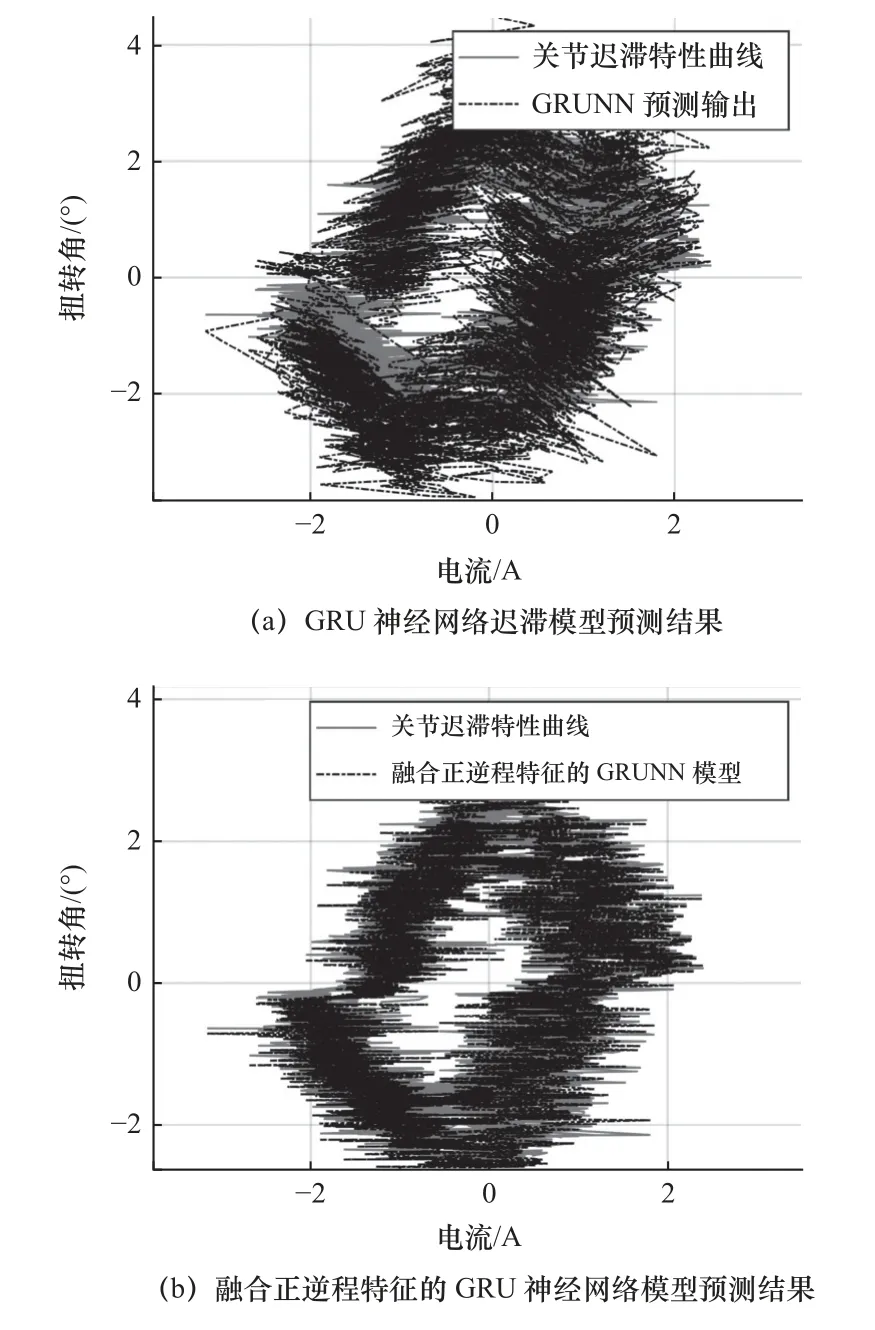
图16 周期为13 s 的迟滞特性预测结果对比图

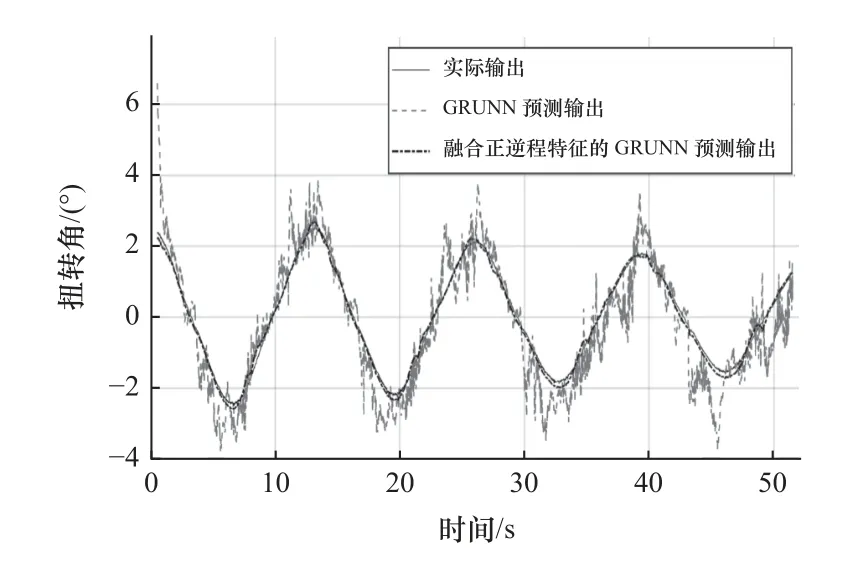
图17 周期为13 s 的迟滞特性预测输出时域展开对比图

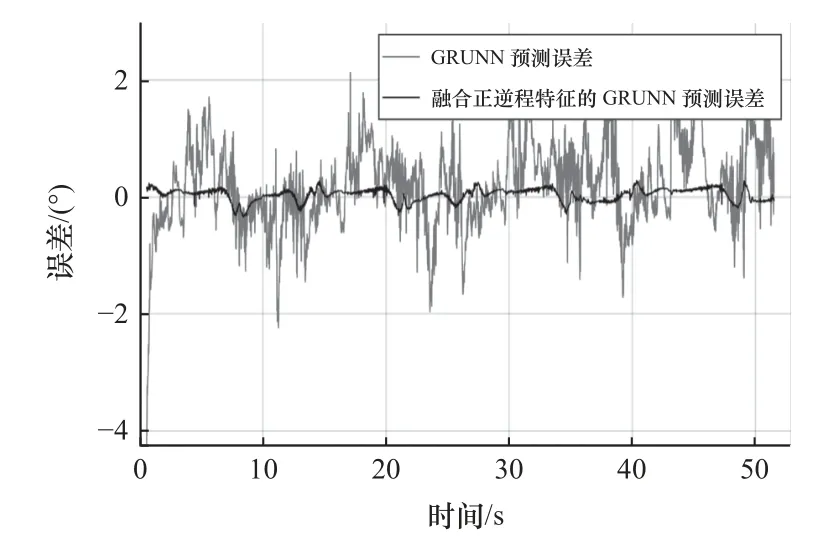
图18 周期为13 s 的迟滞特性预测误差对比图

3.3 实验结果比较分析

表1 为GRU 神经网络迟滞模型和融合正、逆程特征的GRU 神经网络迟滞模型对机器人柔性关节在正弦衰减的运动轨迹下产生的迟滞特性的预测结果。使用均方误差评估模型的预测结果之外，考虑到模型的进一步应用更关注预测结果的最大误差。所以，表1 使用均方误差和最大误差两个指标对所构建的关节迟滞模型进行综合预测结果对比。

表1 两种模型对正弦衰减信号产生的迟滞特性的预测结果

由表1 可得，融合正、逆程特征的GRU 神经网络迟滞模型对不同周期下的迟滞特性的预测输出比GRU 神经网络的预测输出的精度有较大提升，其中均方误差平均减少了98.1%，表明正、逆程特征对GRU 神经网络在不同周期信号激励下的迟滞特性建模起到了重要作用。融合正、逆程特征的GRU 神经网络迟滞模型预测输出的最大误差在不同周期下均有下降，随着周期的增加误差减小明显。根据上述实验结果可得，与GRU 神经网络迟滞模型的预测结果相比，融合正、逆程特征的GRU 神经网络迟滞模型可以有效描述不同周期下的柔性关节迟滞特性，具有更好的预测精度。

4 结语

本文针对低成本轻型工业机器人柔性关节未配置负载转矩传感器特点以及往复运动时表现出的迟滞特性，根据机器人关节执行器所提供的有限信息，与输出转矩-扭转角之间关节迟滞特性建模方法不同，采用电机驱动电流-扭转角之间的关系描述柔性关节迟滞特性，提出了一种融合正、逆程特征的GRU 神经网络迟滞模型。其中：①将输入电流信号进行卡尔曼滤波，滤除高斯白噪声的干扰，并将滤波后的信号再次通过卡尔曼滤波以得到合适的电流增量特征；通过卡尔曼滤波去除计算电流增量带来的高频噪声，得到可以反映迟滞特性正、逆程变化趋势的特征信号；使用模型预测输出的历史信息作为神经网络的输入信号构建动态的GRU神经网络迟滞模型，利用GRU 的记忆能力和非线性映射能力对迟滞特性进行建模。在搭建的GLUON 机器人实验平台，对柔性关节在不同频率下的迟滞特性进行预测。实验结果表明，与GRU神经网络迟滞模型相比，本文所提出的融合正、逆程特征的GRU 神经网络迟滞模型能够有效描述不同周期信号激励下的轻型工业机器人柔性关节迟滞特性。