直线电机运动系统输入到状态稳定性分析

徐永明 曹向东 李 旭 刘海波

（①通用技术集团沈阳机床有限责任公司，辽宁 沈阳 110000；高性能精密制造全国重点实验室，辽宁 大连 116024；大连理工大学机械工程学院，辽宁 大连 116024）

精密运动系统是光刻机、引线键合机以及高端数控机床等高端装备的关键部件之一，其性能的优劣直接影响装备的工作效率和最终产品的品质。如何实现系统精密运动一直都是高端装备制造领域研究的热点和难点[1]。在高端设备的性能要求下，“直接驱动”越来越受到重视，其本质就是取消从驱动器或原动机到工作负载部件之间的机械传动环节，由驱动器或原动机直接驱动工作机构运动，实现所谓“近零传动”。直线电机运动系统就是一类典型的直接驱动系统。系统中的直线电机直接提供推力给负载平台，不需要任何中间传动机构，使得系统具有损耗低和响应速度快等特点，能够提供高动态响应速度和加速度、高定位精度、高刚度以及平滑的无差运动。因此，直线电机运动系统在高端装备制造领域获得广发应用[2]。

然而，直线电机运动系统“零传动”特性消除了机械运动变换机构等不良影响，却也给控制增加了难度，负载变化等干扰都会无衰减地直接加到控制系统中，影响了伺服系统的性能，同时直线电动机所固有的端部效应、齿槽效应以及永磁体磁链纹波等所产生的推力纹波、摩擦阻力的非线性变化等因素都会降低系统的伺服性能，影响系统的精度。所以在设计系统控制器时要充分考虑这些因素的影响，对这些因素加以抑制。因此，有效地提高直线电机运动系统抗扰性能对实现系统快速精准运动是至关重要的。为此，研究人员开展了大量的研究，取得了丰硕的成果。在直线电机运动系统扰动建模与估计方面，Yang R 等[3]在建立直线电机运动系统的动力学模型中考虑了电气子系统参数的时变性和外部的复杂非线性扰动，并在位置控制模式下对推力波动等扰动进行了估计和特征分析，在此基础上建立了扰动及其各阶导数的扩张状态模型。Zhang W J 等[4]研究了直线电机推力波动的周期性特性，利用迭代学习算法不断地修正推力波动的动力学模型，从而达到更好的定位控制精度。Liu Y D 等[5]基于增量卡尔曼滤波器实现对直线电机推力波动的有效观测，相比传统的卡尔曼滤波器，提高了运行效率与观测精度。Cho K 等[6]针对参数不确定性，摩擦力和推力波动的辨识问题，通过状态相关扰动特征的分离与识别，实现系统辨识准确性的提升。Zhang G Q 等[7]在扩张状态观测器的基础上分析推力波动特性，并引入辅助模型，进一步估计和补偿残余推力波动。在扰动抑制控制方面，由于PID 闭环控制器的高鲁棒性和易用性，仍具有很强的适用性，程什祥等[8]结合改进的鸡群算法和PID 控制器，提升了PID 控制器调参的精准性，实现更好的控制器自适应能力。Man F 等[9]基于直线电机速度检测不精准的问题提出一种基于PID 神经网络的速度闭环控制策略，使用梯度下降算法更新参数并拟合电角度，提升了系统的鲁棒性。Zeng D H 等[10]针对直线电机垂直力和横向力对负载的扰动问题，提出了一种基于PID 控制器的3D 电磁力解耦控制策略，设计了新型推力观测器及推力控制器。由于直线电机运动系统对扰动十分敏感，传统的PID 控制器由于可调参数有限，控制器性能的进一步提升受到极大制约，因此，PID 控制器结合扰动观测器的控制策略越来越受到关注。Qu L 等[11]为了改善直线电机闭环控制中的相位延迟和振荡问题，设计线性扩展观测器实现电机反电动势的精确观测，结合PI 控制器，实现电机位置的精准控制。Liu X F 等[12]利用龙伯格观测器预测并补偿非线性扰动，利用前馈控制器提升系统的动态性能，结合PI 控制器保证系统的鲁棒性。随着控制理论的发展，涉及控制理论的控制策略被越来越多地应用在直线电机运动系统中，Huang M F 等[13]提出一种改进型自适应滑膜控制器，更好地估计和补偿具有重复特性的推力波动。Chen Z 等[14]基于μ 综合自适应鲁棒控制器设计了直线电机控制器，在改善鲁棒控制器过于保守的缺点的同时保证了系统的抗扰性。Shao K 等[15]为提高直线电机定位器的跟踪性能，开发了一种基于障碍函数自适应滑模的鲁棒跟踪控制器，提高了直线电机抗扰性。Liu Z T 等[16]提出一种基于梯度下降算法的B 样条小波神经网络控制器，利用李雅普诺夫理论证明了其稳定性，降低了系统不确定性的影响。

本文围绕扰动对直线电机运动系统状态的影响开展研究，建立直线电机运动系统模型，研究系统的输入到状态稳定性分析问题，寻求扰动对系统状态的影响规律。本文提出一种基于李雅普诺夫方法的直线电机运动系统输入到状态稳定判据，分析控制器增益与系统输入到状态稳定之间的关系，为控制器参数的选取提供理论依据。

1 直线电机运动系统模型

直线电机由旋转电机转化而来，其运动原理与旋转电机基本一致，运动的输出都是通过导体在变化的磁场中受电磁力的作用产生的。故在分析直线运动平台的数学模型时，可以将其类比旋转电机驱动系统。

为了方便建模和分析，做出如下假设：

（1）电机参数时不变，保持稳定。

（2）磁场分布是均匀的。

（3）忽略磁滞效应和磁体之间的阻尼作用。

（4）不考虑温度变化对系统的影响。

永磁同步直线电机的矢量图如图1 所示。

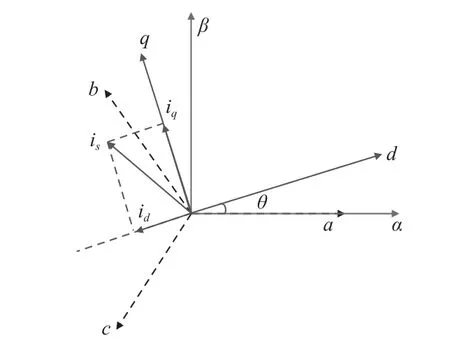
图1 永磁同步直线电机矢量图

a-b-c轴坐标系、α-β轴坐标系、d-q轴坐标系分别为直线电机三相静止坐标系、两相静止坐标系和相互垂直的两相旋转坐标系。

1.1 a-b-c 轴坐标系下的直线电机模型

直线电机由旋转电机演化而来，其模型与旋转电机相似，故直线运动平台在a-b-c轴坐标系下的电压方程表示为

磁链方程为

式中：ψs为三相绕组的磁链，Wb；Us为三相绕组的相电压，V；Rs为电阻，Ω；is为电流，A；Ls为三相绕组的电感，H；ψf为永磁体磁链，Wb；θe为电气转角，rad。且满足

式中：Lm为定子互感，H；Ll为定子漏感，H。

1.2 d-q 轴坐标系下电机模型

分析永磁同步直线电机最常用的方法是建立dq轴数学模型。其思想是将a-b-c轴下的数学模型通过Clark 变换及Park 变换转换为d-q轴下的模型。d-q轴模型下的磁链方程：

式中：ψd、Ld、id分别为d轴的磁链（Wb）、电感（H）和电流（A）；ψq、Lq、iq分别为q轴的磁链（Wb）、电感（H）和电流（A）；ψf、Lf、if分别为永磁体产生的基波磁链（Wb）、等效电感（H）和等效电流（A）。

d-q轴上的电压方程为

式中：ud、uq为动子d、q轴电压，V；Rd、Rq为d轴和q轴的电阻，Ω，其值都等于定子电阻，为Rd=Rq=Rs；v为直线电机线速度，m/s；τ为永磁体极距，mm；p为微分算子。

d-q轴上电流的3/2 变换为

电压与磁通的3/2 变换也与电流类似。

直线电机电磁推力的表达式为

id=0 控制是目前应用范围最广的矢量控制策略，即令动子电流矢量与定子永磁体磁场在空间上正交，从而使定子绕组中d轴的电流分量为0，定子电流中只包含q轴电流分量，即只包含推力电流分量。由此可得电磁推力Fe及电压方程为

根据直线运动平台的运动学特性，可得直线电机模组的机械运动方程为

式中：Fload表示直线运动平台的负载阻力，N；Bv表示粘滞常数，N·s/m2；M表示直线电机模组运动部分的质量，kg。

由式（7）～式（9）可将直线运动平台的简化模型写为

由1.1 节分析可得，直线运动平台在实际的运动过程中，会受到多种非线性干扰因素，包括由直线电机结构特性导致的定位力波动Fripple、非线性摩擦力Ffriction和负载Fload的变化等，对直线运动平台的输出具有一定的影响。故考虑非线性影响因素的直线运动平台的数学模型可以写为

2 输入到状态稳定性分析

考虑到如下系统：

由于跟踪误差e定义为

则式（12）可表示为

考虑到PID 控制仍然在工业控制中占有重要地位，本文中uq满足如下形式：

将式（16）代入式（15）可得：

定理 2.1 对于给定常数α>0，γ>0，如果存在正定对称矩阵P>0，使得如下不等式成立：

则系统是输入到状态稳定的且系统状态满足

式中：λmin(P)为矩阵P中最小的特征根，λmax(P)为矩阵P中最大的特征根。

证明：构造如下形式的Lyapunov 函数：

显然V(t)满足如下条件：

由式（18）可得：

由式（18）和式（21）可知，式（24）正确。

显然系统是输入到状态稳定的。证毕。

当ω(t)=0，定理2.1 可以退化为如下推论。

推论 2.1 对于给定常数α>0，γ>0，如果存在正定对称矩阵P>0，使得如下不等式成立：

则系统是指数状态稳定的，且系统状态满足

式中：λmin(P)为矩阵P中最小的特征根，λmax(P)为矩阵P中最大的特征根。

3 算例分析

本部分利用所提方法分析某直线电机运动系统的输入到状态稳定性问题。系统的主要参数为：电磁推力常数Kf=124 N/A，粘滞常数Bv=0.2 N·s/m，电机运动部分质量M=5 kg，单相电阻Ra=5.3 Ω，单相电感Lq=9 mH，极距τ=57 mm。利用Matlab 中Yalmip 优化工具箱，根据定理2.1（α和γ为给定常数），可以获得不同控制器参数与系统输入到状态稳定性之间的关系。计算的结果见表1。

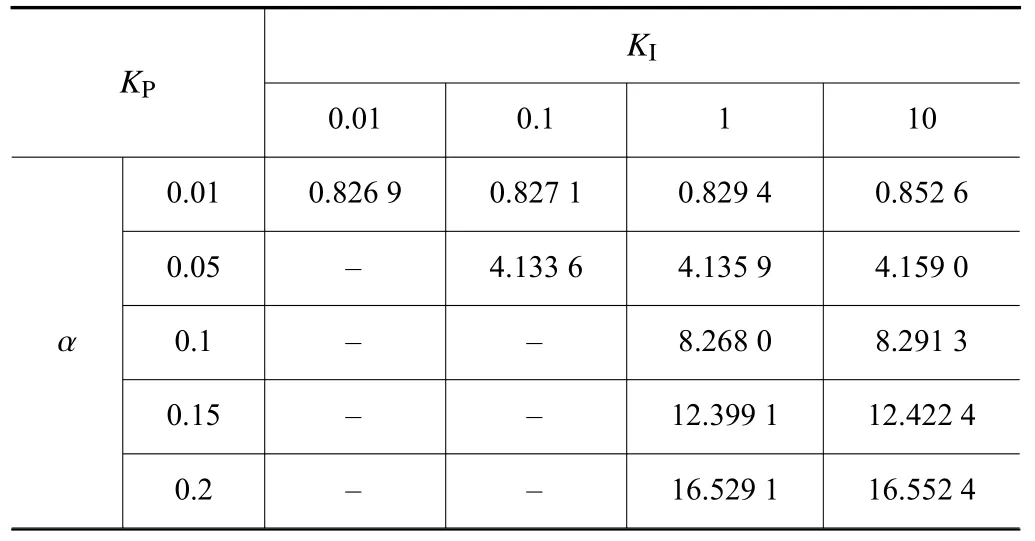
表1 保证系统输入到状态稳定的 KP最小值

图2 系统跟踪误差稳定曲线

4 结语

针对直线电机运动系统进行了建模，研究了此类系统的输入到状态稳定性分析问题，提出了一种基于李雅普诺夫方法的直线电机运动系统输入到状态稳定判据，建立了控制器增益与系统输入到状态稳定判据，以及控制器增益与系统输入到状态稳定性之间的关系。本文的研究可为控制器增益选取提供一定的理论支持。