一种数控小线段拟合与速度规划的优化方法*
缪 睿 张永林
(江苏科技大学自动化学院,江苏 镇江 212003)
数控加工中为避免频繁启停机床和速度突变带来的过冲、振荡导致的机床和刀具损伤,通常采用曲线拟合尖角轮廓,牺牲部分精度,以一段弧线近似代替尖锐拐角,这样一来,瞬间突变的速率和方向被整条弧线分担,有效解决了前述问题。
曲线拟合的本质是分解为更多的离散点,以更密集的弦逼近计算得到近似弧线,比较流行的有等间距法和最小误差法等。目前应用较为广泛的方法为B 样条的曲线拟合,但一般的B 样条拟合更适合全局拟合,难以控制局部拟合精度。对此,封雨鑫等[1]提出了一种基于三次B 样条曲线高精度拟合连续小线段的方法,通过转角和双边弓高误差分析确定型值点,但该方法仍然是通过多等分获取弓高误差,存在一定偏差。为了使参数曲线拟合保持精度,盖荣丽等[2]提出了一种基于特征提取,最小二乘逼近法以及粒子群优化算法求解的曲线拟合方法,建立粒子种群和衡量误差的适应度函数,但未对弓高误差提出解决方法,且多次到达迭代最大次数,牺牲了更多的时间,实时性受到影响。高秋英等[3]对最小二乘法曲线拟合及优化进行了研究。梁小兵等[4]将误差面上下移动,使单方向的误差出现在拟合线条两侧,另一侧误差直接舍去,误差被压缩为原本的一半,但此行为直接牺牲了加工面的限制作用,这种加工方式随时可能出现刀具超出距离的情况,不满足单向限制。冯倩倩等[5]基于曲率连续的混合曲线进行了插补相关研究,进一步提高了加工轮廓的光顺性。
为实现曲率连续,增加插补过程稳定性,同时保持曲线计算的低复杂度,便于误差等参数的计算,本文提出一种基于三角正弦曲线的空间光顺拟合方式。首先对空间中折线降维,根据每个拐角的三个控制点间的信息,确定弧线的系数、周期,根据允许的最大弓高误差,进行二次切进偏移,计算出弧线上的离散点,避免迭代的耗时,然后利用速度前瞻中的回溯法,完成空间中的轨迹规划。
1 三角曲线拟合实现
1.1 拐角处理
采用局部光顺拟合的方式,截取各局部拐角降维后分别处理。为避免拐角间各自处理时的相互干涉,取拐角两边较短者的一半作为生成三角曲线的最大过渡边长。
三角曲线在[0,π/2]周期内斜率从1 开始衰减至0,而直线斜率不变,所以改变后的正弦曲线仍和圆弧一样,不会在侧边出现过处理从而引起误差。
三角曲线的表达式为
式中:假设三角的高为h,底长为c,则斜率k=2h/c,频率ω=π/c。
最大误差E量化由计算得约为0.363h,通过k和ω确认当前取值最大误差E是否符合要求,若不符,则以允许的最大误差Er为基准,缩短过渡边长tr:
式中:Er为工艺要求允许的实际加工轨迹偏离预定轨迹的最大距离,tr为从实际轨迹开始偏离预定轨迹处到该段小线段结束的距离。
除等腰三角范围外,轨迹保持为原来的直线段。
1.2 过渡边长对比
如今较为广泛使用的插补方式为圆弧插补和B样条插补[6],其中B 样条插补由贝塞尔样条一般化而来,但更复杂:定义域被节点细分,且基函数Ni,k(u)是一个在u上的p次多项式,在整个区间非负。B 样条曲线定义公式如下:
式中:Pi为控制点序列,计算结果C(u)则为B 样条上的点。
B 样条可以较好地拟合曲线,但更适合全局拟合,且由于其公式复杂性,其局部偏差和弓高误差难以计算[7]。
局部偏差可利用B 样条曲线的强凸包性解决-在特殊位置选取更多的控制点[8],可成功控制最大偏差,或者利用clamped B 样条曲线的性质之一分段画出B 样条[9]:选取合适的控制点使两条独曲的B 样条曲线光滑连接,如图1 所示。
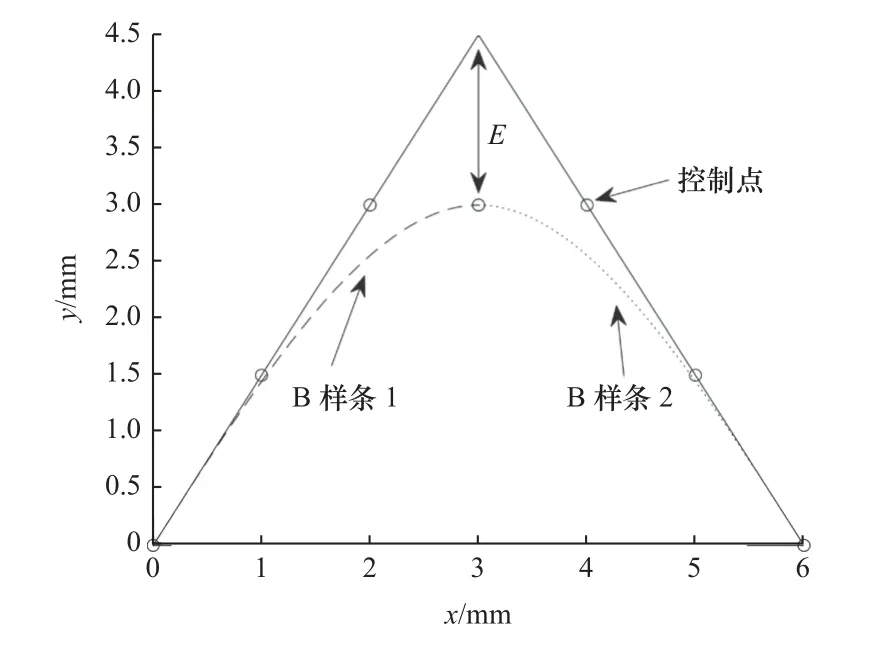
图1 clamped B 样条曲线分段插补
即使解决了偏差的控制,依旧存在产生的插补线形状怪异或计算复杂度过高且无法保证精确度的问题。
而对于正圆弧线,已知角度θ(拐角的一半)和最大允许偏差Er后,可以计算出该情况下插补圆弧的半径r,最后算出过渡边长trcircle:
正弦弧线的求取则依据弧线的峰值和最大允许偏差Er的关系,得出所需的拐角高度h,求出过渡边长trsine:
最大允许误差E和角度θ都固定后,可以画出具体图像,如图2 所示。可以看到,在相同拐角下保证最大偏差相等,正弦曲线的过渡边长L比圆弧曲线的过渡边长L'长。
由式(4)和式(5)可得,当过渡边长越短时,产生的偏差也越小,当过渡边长相等时,正弦弧线会产生更小的偏差,而偏差相等时,若拐角边长足够,正弦弧线也会使刀具在运动时获得更长的过渡时间,减小刀具的损伤。
1.3 插补设计
1.3.1 插值点计算
插补本质仍为在更短的小线段上直线行进,插值点标准一般为两点间线段与弧线的弓高误差e。
而B 样条曲线很难通过弓高误差来判断获取插补点,需通过当前位置、速度等信息二阶泰勒展开计算下一个插补点,插补点间弦长和插补曲线的弓高误差也无法精准算出,只能取近似值[10]。
圆弧插补由于弧线曲率固定,e确定时弦长也固定,都可以精确计算,单个拐角仅需计算一次即可得出所有插补点,但正弦线曲率在变化,所以需要分别计算。
对弧线内部的插补点进行处理:由前述可知正弦最高处为k/ω,则可求得Xn。
从其下一个点Xn-1开始则难以计算,若需要较高的精度,则需迭代法求出,迭代标准为弓高误差e,假设当前点为Xi迭代步骤如下:
(1)获取当前点和上一点间的斜率。
(2)找到弧段上斜率相同的点。
(3)求得该弦弓高D。
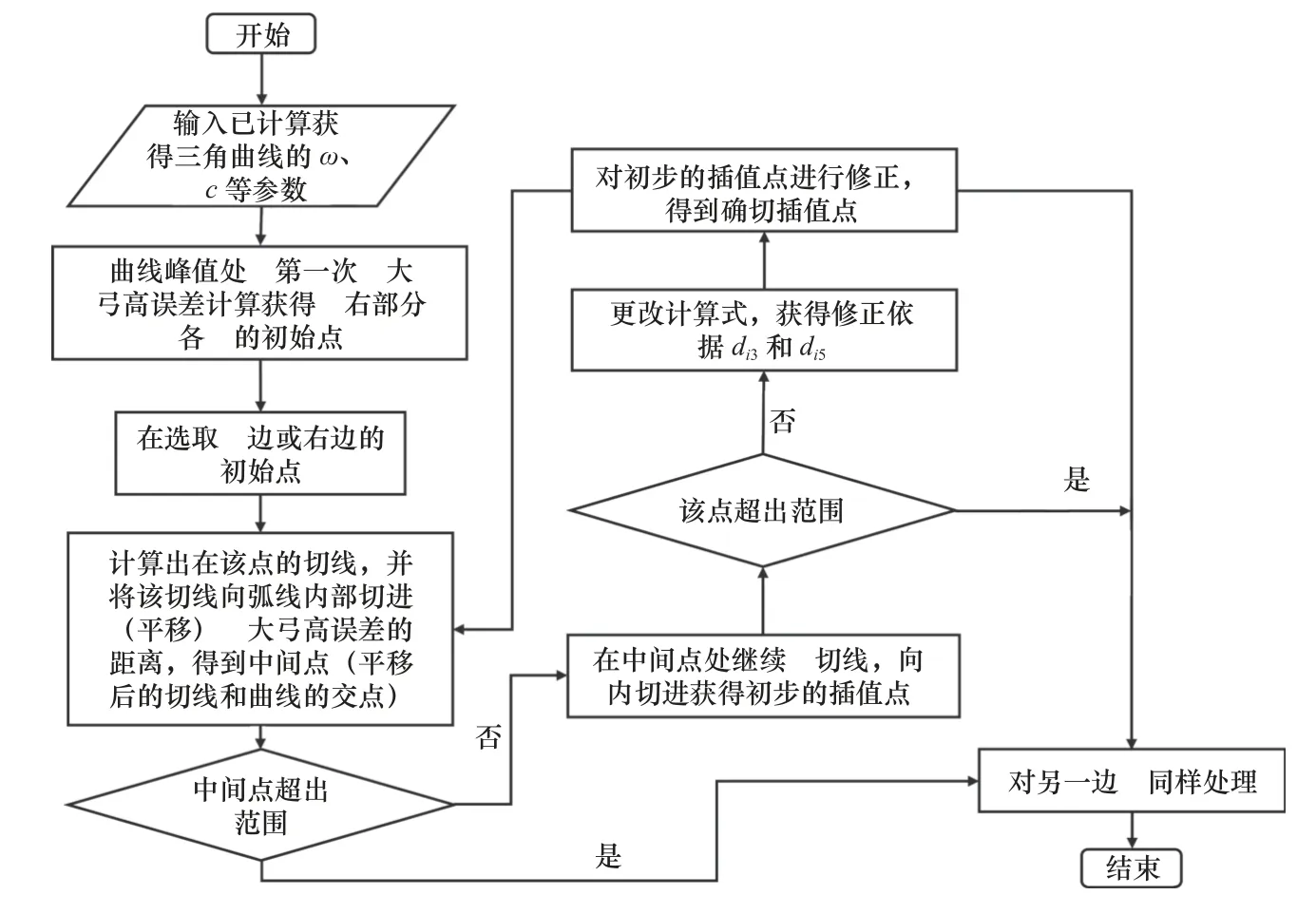
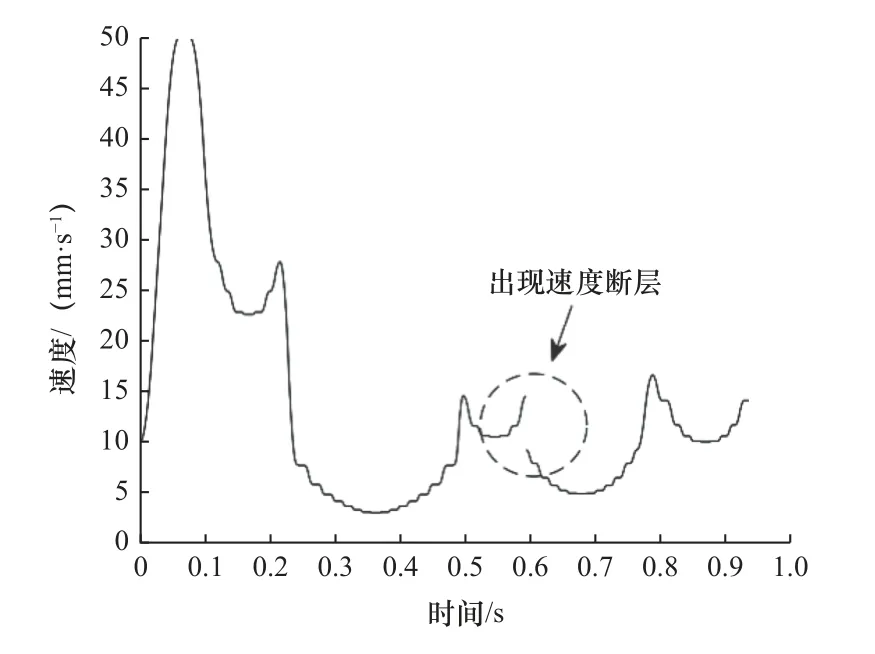
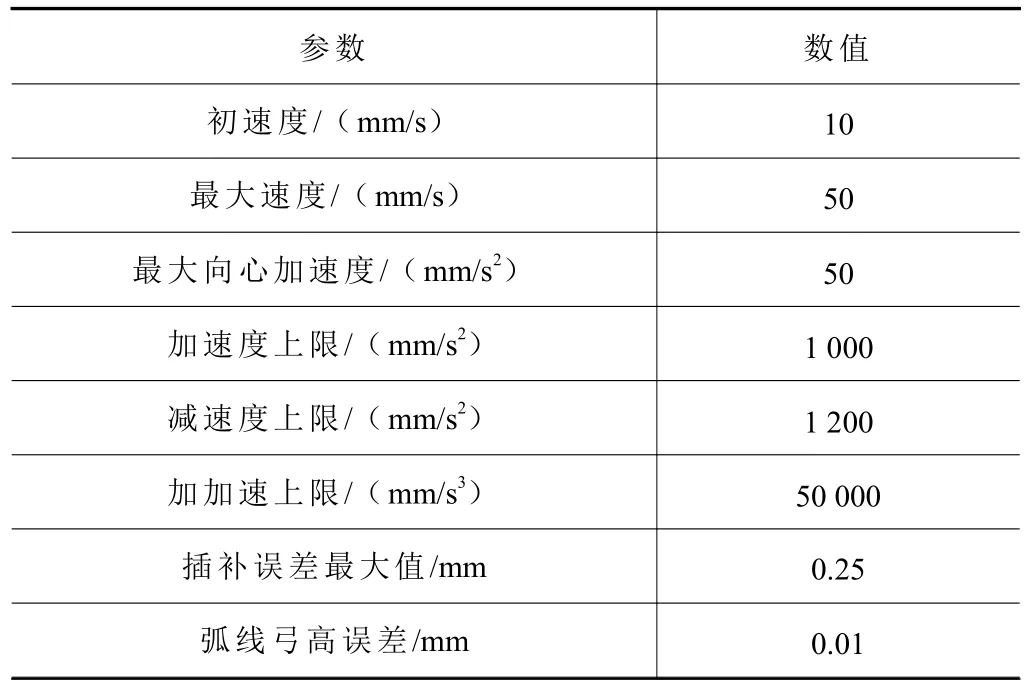
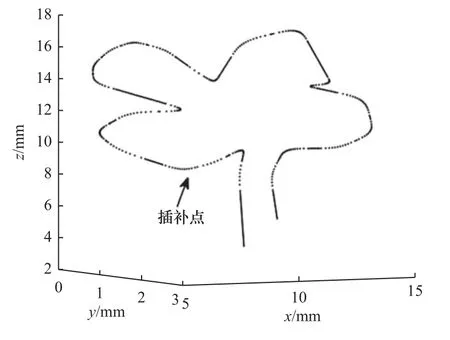
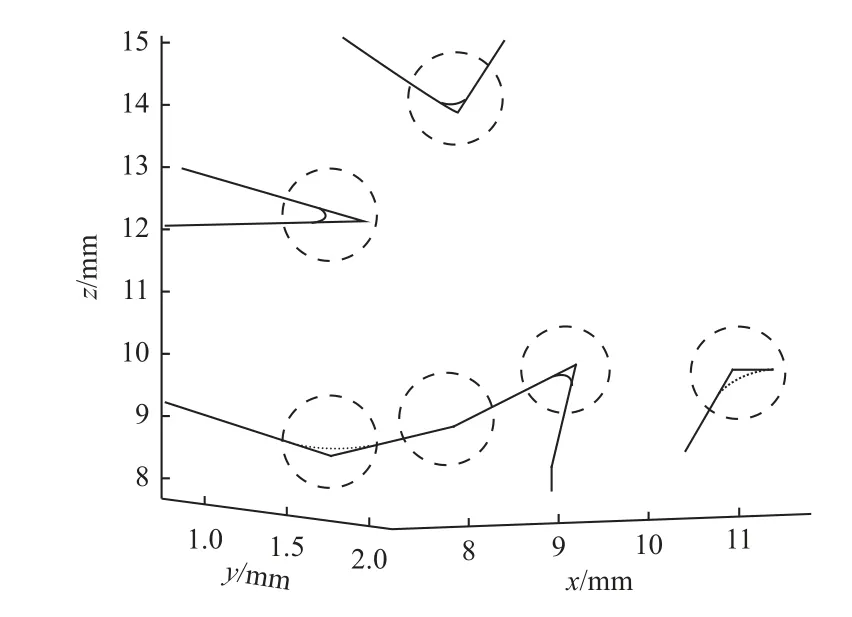
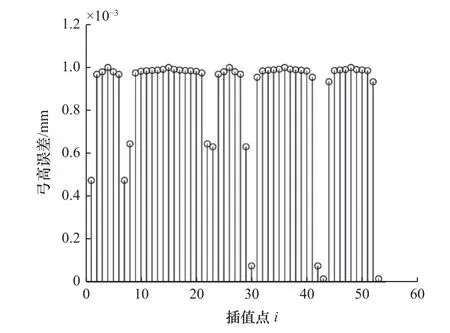
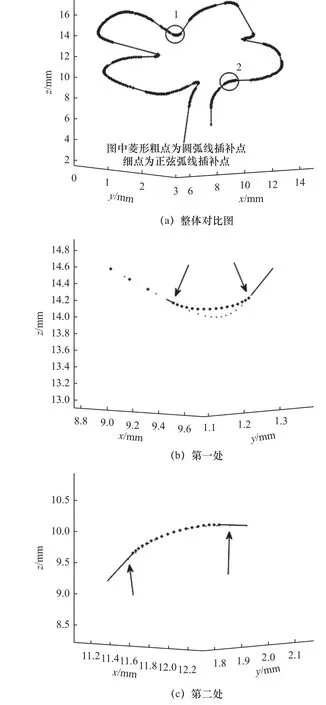
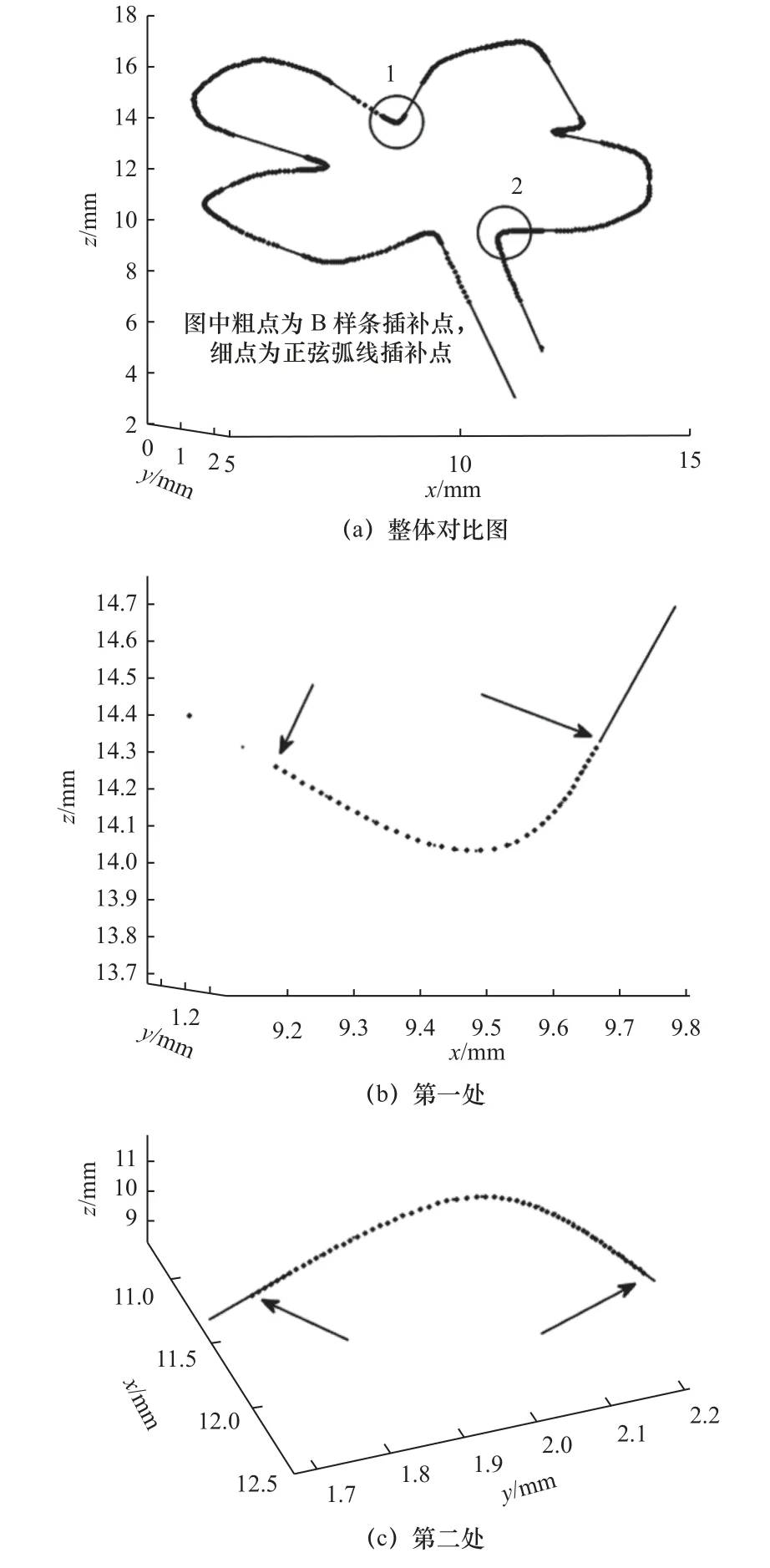
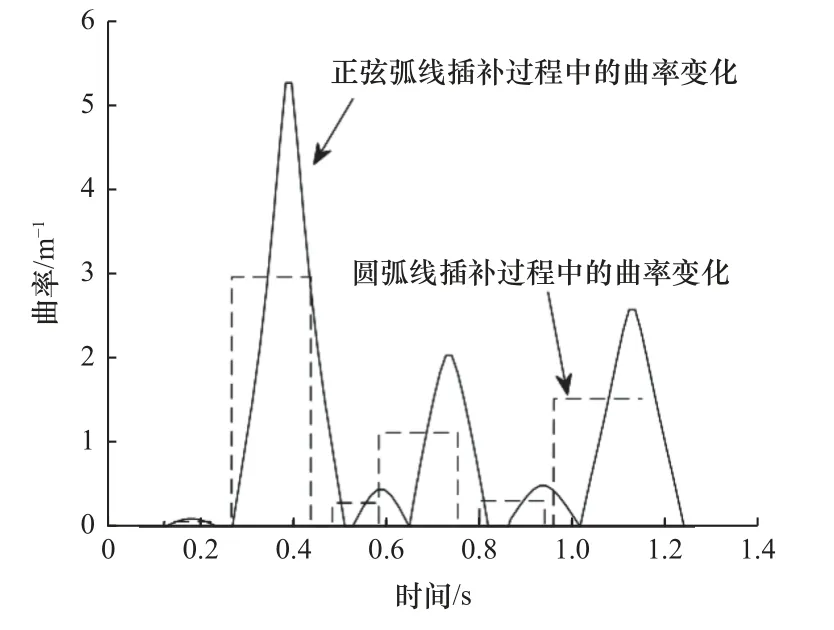
(4)若D与e误差在允许值内,则停止迭代,否则,取上下限的中值为新的di,若当前D>e,将当前di设为上限;若D (5)直至求出X1(X1与原点间弦的弓高小于等于e)。 迭代计算虽然能得到较好的插补精度,但存在迭代次数不固定、计算耗时等问题,难以满足实时性要求。对此,提出另一种算法。 (1)如图3 所示,在Xi处做出其切线L1,根据已知条件可得L1的表达式: 图3 插补点近似算法 式中:ki和Ci1为点Xi处切线所需的斜率及截距值。 (2)向内切进弓高误差的值e,得出另一条线L'1,表达式如下: 式中:Ci2为切线切进变化后的截距值。 (3)计算L'1与正弦曲线的交点X'i: 这个式子没有符号解,无法精确求出,所以需要将三角函数部分进行泰勒展开。同时,为尽量提高计算准确度和降低计算阶次,需要进行变化。 先改用两点间的差分值表示X'i,转换后的式子变为 式中:d为两点间的差分值,即X'i=Xi-d。 最后,把包含未知项d的部分泰勒展开,正弦展开至一阶,余弦展开至二阶,求得d的根di1和di2,互为相反数,取正根di1,即可求出X'i。 (4)对X'i在进行(1)~(3)步骤的操作,再得到一个正根di3,Xi减去di1和di3后即求得前一个插补点Xi-1。 (5)重复(1)~(4)步骤,可依次求出各插补点。 (6)当出现当前插补点减去所求差分后为负数的情况,就代表计算结束,当前点作为第一个插补点。 在该算法中,为了保证算出的插补点间弓高误差的精度,引入sigmoid 函数对二次切进初次取得的点位进行修正,修正规则如下。 第二次切进计算得到前述中的前向距离正根di3后,将算式修改至如下,算出d的后向距离正根di5: 随后判断修正方向,若需前向修正,则修正值redress为 式中:dis为di1和di5的差值,若dis为负,则表示取得的点与上一个插值点间弦线和拟合线的弓高误差小于e。 此时真正的Xi-1需要在二次切进求出的点的基础上减去redress。 若dis为正,则代表弓高误差超限,需后向修正,后向修正的redress的值通过式(11)中根号下算式中的di3变为-di5得到。 此时真正的Xi-1需要在二次切进求出的点的基础上加上redress。 流程图如图4 所示。 图4 求取插值点的流程图 1.3.2 正弦弧线上插补间速度计算 计算时,为了更快地获得速度信息,需要进行速度前瞻相关计算[11],提前计算出当前时刻后一段时间的速度,用于平滑速度曲线[12]、保护机器和零件。 首先,计算未划入拐角的直线部分速度,采用7 段式速度规划:由用户设定初速度vs、最大速度vm、最大加速度accm、最大减速度decm和加加速jerk。 式中:Ti(i=1,2,···,7)值和加加速函数j(t)、加速度函数a(t)以及路程函数s(t)在石川等[13-14]的数控系统S 曲线加减速规划研究中给出了具体算法。 计算时,由于对称性,只需计算前半段:其中第一段由于长度不可控,选择以匀速进给,速度为第二个插补点的允许速度,最后一段情况相同。 从第二段开始,单段弦本身长度较短,不进行七段式处理,只看作两段处理。 计算方式:假设只有减加速和减减速两部分,以正常速度计算该情况下会进给的距离Sper: 如Sper大于等于弦长S,代表可用该速度在此弦长上进给运动,多余的弦长部分则以初速度在弦开始的部分进给。 此时: 式中:t1、t2、t3分别为加工过程中的减加速、匀减速、减减速的时间。 如Sper小于S,表明两个插补点间的弦长长度不足以在外部给定的加加速下完成速度变化,方法之一是通过S强制调整增大jerk(此时,已进入强制规划)。 以上处理方式保证了单个拐角内速度连续,但拐角间未做处理,此时速度图像如图5 所示(图中为四叶草前5 个拐角点间的速度,设置的参数为加速度上限为1 000 mm/s2,减速度上限为1 200 mm/s2,加加速上限50 000 mm/s3)。 图5 弧段间速度曲线出现断层 图5 中,当拐角间不存在缓冲段时,会直接出现断层现象。具体表现为速度曲线突变,仿真软件内部可看到加速度的内部存储值为NAN,加加速内部存储值为-Inf。 1.3.3 解决速度断层问题 为解决这一问题,同时保证实时性,速度前瞻时选用回溯法。 回溯法的基本思想为先取用一定数量的线段作为前瞻段,从末尾向前回溯处理,计算出各拐角的允许速度,调整每个拐角的速度,调整结束后,加入一段新线段作为新的前瞻段,重复上述步骤,直到处理完最后一段前瞻段。 加入速度前瞻回溯法解决速度连续问题后,还存在较为明显的缺陷,即每次插补时的弧线曲率是突变的。而正弦弧线的曲率则是从零开始,连续变化,保证了稳定性。 为评估本文提出的正弦曲线插补和速度规划算法的有效性,利用Matlab 仿真软件进行仿真实验。 在空间中利用点位信息构造一个立体的四叶草形状,直接用折线相连的结果如图6 所示。 图6 四叶草折线图 按照工程中一般的要求,插补最大误差值设为0.25 mm,弦长弓高误差为0.01 mm,其他参数设置见表1。 表1 各插补参数 用正弦曲线插补算法插补后结果如图7 所示。 图7 光顺后的四叶草图 将两张图叠加在一起,并进行局部放大,结果如图8 所示。 图8 插补前后局部对比 其中各插值点经过计算并修正后部分弓高误差如图9 所示。 图9 修正后的弓高误差(部分) 可知,除边界外,拐角内部点的弓高误差精度都控制在10%以下,进一步计算可得,误差控制在8%以内。 当固定最大允许误差E为0.25 mm 时,改变角度θ,正圆弧线和正弦弧线所需的过渡边长如图10 所示。随着角度θ的增大,正弦弧线的过渡边长始终长于圆弧线。 图10 正弦弧线和圆弧线过渡边长对比 将正弦弧线插补和圆弧插补的图叠加对比如图11所示。 图11 正弦和圆弧插补的对比 通过图11b 可看出,当拐角边长同时小于圆弧插补和正弦弧线插补所需的过渡边长,即相同拐角下两者过渡边长相等时,正弦弧线插补有着更高的精确度。 而图11c 中的拐角边长足够,正弦弧线比圆弧更早进入插补过程,从而获得更长的过渡,减小对刀具的损耗。 计算拐角在[π/6,2π/3]范围内过渡边长的比值,结果如图12 所示。 图12 过渡边长比较结果 可以看出,同个拐角下,正弦弧线插补的过渡边长可比圆弧插补长47.5%~118%。 计算可得,在最大偏差E同为0.25 mm 时,满足圆弧插补120°角度的过渡边长用于正弦弧线插补最小可满足85°,满足102°角度的圆弧插补过渡边长即可满足最小30°的正弦弧线插补过渡,即相同过渡边长限制下,正弦弧线插补范围比圆弧插补可扩大29%~70%。 B 样条曲线由于自身的特性,可通过对控制点的处理或分段来对最大误差进行修正[15],为保证对比效果,将B 样条拟合的偏差修改为与正弦一样的大小,对比图如图13 所示。 图13 正弦和B 样条插补的对比 相比之下B 样条插补对过渡边长并无特殊要求,表现在代表B 样条的大插补点完全覆盖了过渡边长的部分,并没有更多的实线出现,灵活方面优于圆弧和正弦插补[16]。 但因为计算的复杂度和不规则性,需要更长的运算时间,难以确定插补点产生的弓高误差最大值位置,将这个方面列入考虑,误差的精确度上是圆弧和正弦插补更高。 同时,添加回溯法对其各个拐角速度进行限制处理前后,速度得以连续、加速度、加加速曲线也不再有超限问题,速度以及正弦弧线和圆弧插补过程中曲率变化分别如图14 和图15 所示。 图14 加入回溯法前后的速度曲线 图15 正弦弧线和圆弧插补过程中曲率变化图(部分) 由于回溯法的限制,当提高最大速度超过一定范围后,速度曲线将保持不变,保证了加工过程的连续性和可靠性。 同时,正弦插补的方式也改进了圆弧插补的曲率突变问题,使得插补过程更加稳定。 本文提出一种基于圆弧插补方式的正弦弧线插补方法,将圆弧插补中的正圆弧替换为正弦曲线,克服了正圆弧插补中曲率不连续的问题,同等最大偏差和过渡边长限制下,正弦弧线插补的适用范围比传统圆弧插补多约29%~70%,更具灵活性。 由于正弦曲线的曲率处处不相等,无法快速精确地求出插补点,采用迭代计算又会有耗时、实时性降低等问题,转而提出一种两次切进向前延伸寻点的方法,并同时加入泰勒展开和sigmoid 函数近似求出插补点并修正,保证了实时性,避免迭代的同时实际取点值与期望点值相差均值也在8%以下。 在拐角内部,通过简化的S 型速度算法,加入盛金公式解速度方程,保证内部速度连续,外部则通过速度前瞻中的回溯法解决断层问题,保证内外速度都连续,提高稳定性,保护刀具,延长机床寿命。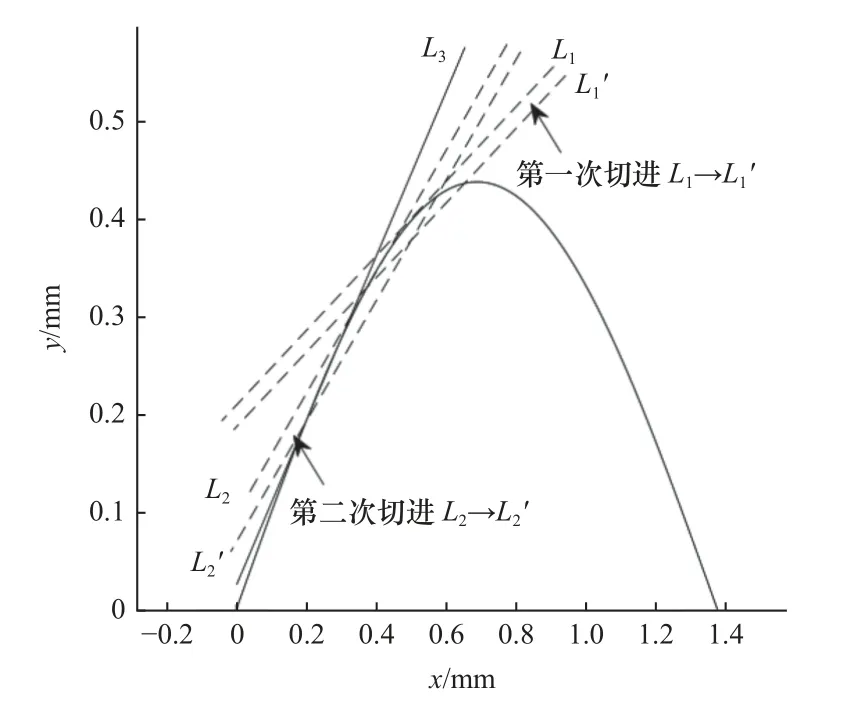
2 实验仿真




3 结语

