改进离散粒子群算法的多无人艇任务分配研究∗

赵冬梅 宋 阳 周国军 崔海峰

（海军大连舰艇学院基础部 大连 116018）

1 引言

无人艇（USV）结构简单，价格低廉，安全性好，适合在危险区域执行搜救、侦察、巡逻、打击等多种任务［1～2］。2022年6月7日，我国首艘全国产化的百吨级无人艇在舟山海域顺利完成首次海上自主航行试验，标志着我国无人艇自主航行和智能机舱技术取得了新的突破［3］。随着无人艇技术的发展，在未来战场上，无人艇将大显身手，成为海战的主力。

任务分配是多无人艇协同控制技术研究的关键环节，是在复杂的战场环境中，在满足一定的约束条件下，为各无人艇分配任务并确定任务时序［4］。任务分配模型可分为集中式、分布式和混合式三种，相较于分布式和混合式模型，当执行的任务间具有强约束时，集中式模型的全局求解能力更强，任务分配质量更好［5］。集中式任务分配模型的典型求解算法包括匈牙利法［6］、混合整数规划算法［7］等最优方法和聚类算法、智能算法［8～12］等启发式求解方法。

相比于其他算法，智能优化算法以其概念简明、实现方便、参数设置少、鲁棒性强［13］等优点越来越受到研究学者的青睐。文献［14］将约束融入到算法的粒子矩阵编码和粒子更新策略中，有效解决了多类复杂约束条件下的任务分配问题；文献［15］设计了双层粒子群编码方法，基于启发信息和冲突消解策略改进粒子群算法，提高了算法的收敛性和全局搜索能力；文献［16］将粒子速度和坐标离散化，改善基本粒子群不易处理离散问题的缺陷，实现了对舰载机弹药的合理调度，但没有对粒子的位置和速度更新公式加以改进，算法的收敛性和灵活度不高；文献［17］应用离散粒子群算法解决消防救援队伍在现场使用无人机时存在的多任务分配难题，提出引入逆转算子对算法进行优化，提高了分配结果的可靠性和科学性，但没有解决算法易陷入局部最优问题；文献［18］整合离散粒子群算法和Logistic 混沌算法，避免算法陷入局部最优，但没有改善算法的收敛性。

本文针对多无人艇打击多目标的任务分配问题，考虑时间窗约束和载荷约束，建立问题模型，确定评价函数。综合上述文献对离散粒子群算法改进的优缺点，提出一种新的改进思路：初始化粒子群时利用Logistic 方程融入混沌优化，以增加种群搜素初期的多样性；为提高搜索效率，改进惯性因子，设置其随迭代次数呈指数递减分布，以适应不同时段的算法要求；设计随迭代次数分别递增和递减的学习因子c1和c2，以平衡算法的局部搜索能力和全局搜索能力；完善粒子速度和位置更新机制，融入交叉和变异操作，以解决算法陷入局部最优和收敛速度之间的矛盾。最后通过仿真实验验证改进算法的优越性。

2 任务分配问题建模

2.1 问题描述

假设在5km×5km 的海域内有m 艘无人艇S={S1，S2，...，Sm}，到达n 个待打击的目标点T={T1，T2，...，Tn}执行打击任务，无人艇Si携带Wi个载荷，在满足多项约束条件下，使无人艇完成打击任务的评价指标最好。

离散粒子群算法对于求解此类非线性整数规划问题具有参数设置简单、执行效率高等优点［19］，建立无人艇和打击目标之间m×n阶的决策变量矩阵如式（1）所示。

xij只能取1 或0，xij=1 表示无人艇Si对目标Tj执行打击任务，xij=0 则不打击。结合实际约束条件和评价函数求解出将m 艘无人艇的载荷分配给n个目标的最优目标分配方案。

2.2 约束条件

1）时间窗约束

构建模型时，通常要求无人艇在指定的时间段对目标执行打击任务，时间窗约束如式（2）所示。

其中，Tj.StartTime_t和Tj.EndTime_t为指定的打击第j 个目标的起始和结束时间，StartTime_o和EndTime_o为实际打击第j个目标的起始和结束时间。

2）无人艇载荷约束

无人艇携带载荷数目有限，即执行打击任务的次数受限，若无人艇Si最多可携带Wi个载荷，无人艇使用载荷约束如式（3）所示。

3）目标载荷约束

为避免出现多无人艇打击目标点过于集中的现象，要求无人艇对某个目标使用的载荷总数有限，即对目标Tj最多可使用Sj个载荷，目标承受载荷约束如式（4）所示。

2.3 任务分配评价函数

评价函数体现无人艇任务分配的优劣程度。本文设计基于完成任务的效益减去航线距离代价和执行任务时间代价的任务分配评价函数，表达式如式（5）。

其中，ωR、ωD和ωT分别为任务效益、距离代价和时间代价的权重系数，体现每项收益或代价的重要程度，可根据实际需求动态调整三项系数以体现任务分配的多原则决策机制。

为减少无人艇暴露时间，提高其执行任务的安全性，以航线距离最长的无人艇行驶距离作为时间代价，v为无人艇航行速度。

上述评价函数兼顾了执行打击任务的收益、距离和时间代价，能够引导种群选择出打击效益高、航行距离短和执行时间少的分配方案。

3 改进离散粒子群算法

3.1 离散粒子群算法原理

粒子群算法是基于种群和进化的概念，通过个体间的协作和竞争，实现对复杂空间最优解的搜索［20］。粒子通过开发和探索，依据最优信息不断更新迭代，速度向量νij和位置向量xij的更新规则如式（6）所示。

式（6）中，νij和xij分别表征第i 个粒子在第j 维空间的速度向量和位置向量；pij表征第i个粒子在第j维空间的个体最优位置；pgj表征粒子群迄今为止在第j 维空间的全局最优位置；w为惯性因子，表征粒子保持原有速度的能力；c1和c2为学习因子，表征粒子对自身的思考；r1和r2为［0，1］间的均匀随机数，以增加粒子飞行的随机性，保证种群的多样性。由上述公式可以看出，粒子群算法的更新规则兼顾运动“习惯”、自身“认知”和“社会”经验，以便更快更准确地搜索出最优解。为避免粒子群的膨胀和发散，通常利用边界约束将粒子速度和位置限制在可行搜索范围内，一般设置最大值和最小值，当超出二者范围时，产生取值范围内的一个随机数代替当前速度和位置值。

离散粒子群算法的思想是将基本粒子群算法中连续域的位置、速度向量离散化，粒子在状态空间的取值只能为0 或1，每一维速度νij代表每一维位置xij取1 的可能性，所以个体最优位置pij和全局最优位置pgj只能在［0，1］内取值，速度更新公式保持不变，而位置更新公式如式（7）所示。

式（7）中，r为［0，1］间的均匀随机数。

利用离散粒子群算法求解任务分配问题时，每个粒子代表一种任务分配方案，根据评价函数计算各个粒子的适应度值，更新个体、全局最优位置和最优值，更新粒子速度和位置，进行边界条件处理，重复上述步骤，直至迭代结束，得到最优分配方案BestDistribution。

3.2 粒子的编码与解码

综合考虑无人艇任务分配的载荷约束条件和一般粒子编码规则，设置粒子的维度为所有无人艇携带载荷的总数D，，Wi为第i 艘无人艇携带的载荷数。为体现任务分配方案，设置每一维粒子代表相应无人艇各个载荷执行任务的目标编号，例如无人艇S1、S2、S3、S4分别携带2、3、2、3 枚载荷，计划攻击6 个目标，如果粒子编码为［1，3，6，4，5，1，0，2，3，5］，说明S1打击1 号和3 号目标，S2打击6 号、4 号和5 号目标，S3打击1 号目标，S4打击2 号、3 号和5 号目标，故粒子编码的取值范围为0 至目标数n之间的整数，0表示不分配该载荷执行任务，当算法迭代出现非整数时，需要对其进行取整处理。

对粒子序列进行解码时，先依据载荷数Wi依次提取每艘无人艇执行任务的目标序号，根据无人艇Si和目标Tj的对应关系，更新位置变量xij的值，载荷被分配时为1，否则置0。

3.3 混沌初始化粒子

混沌优化算法具有随机性、遍历性和敏感性［21］，为提高离散粒子群算法的全局搜索能力，采用Logistic 方程在粒子的初始化时融入混沌优化。一维混沌系统的Logistic映射方程如式（8）所示。

xl+1=μ∙xl∙(1-xl)l=1，2...;μ∊[0，4] （8）其中，l 为迭代次数，μ为混沌系统的控制参数，当μ=4，x1∊(0，1)且x1≠{0.25，0.5，0.75}时，该系统处于混沌状态。

混沌初始化粒子的步骤如下：

1）随机产生取值在0～n 之间的N×D维初始粒子群xori，n 为目标数，N 为种群粒子个数，D 为载荷总数；

2）随机产生一个D 维向量z1=[z11，z12，...，z1D]，根据式（8）得到N个D维向量z1，z2，...，zN；

3）通过初始粒子群xori和z向量相乘再取整的运算规则将混沌的z向量映射到粒子的位置向量，如式（9）所示。

式中，| | 表示取整运算。

3.4 指数型惯性因子

惯性因子是影响算法搜索能力的主要因素之一，是平衡局部搜索和全局搜索能力的重要参数，合理设置惯性因子的更新方法是离散粒子群算法有效实现的重要保证。传统离散粒子群算法设置固定的惯性因子，其值较小时，算法不易收敛，其值较大时，算法易陷入局部最优。为兼顾全局和局部搜索能力，采用较多的是随时间线性递减的动态惯性因子，为进一步提高算法的收敛速度，参考文献［22］，设置如式（10）所示的非线性变化的指数形式的惯性因子。

其中，l 为迭代次数，NC为最大迭代次数，α为控制惯性因子衰减速度的常系数，设置惯性因子w的取值范围在［wmin，wmax］区间内。根据上述设计，惯性因子随迭代次数呈现指数递减分布，突出了不同时段对粒子全局和局部搜索能力的动态调整，极大提高了算法的效率和准确性。

3.5 自适应学习因子

学习因子是反映粒子群信息交流的重要参数，决定粒子个体经验和群体经验对粒子飞行的影响。为提升算法的全局搜索能力，改变传统离散粒子群算法学习因子c1和c2固定不变的机制，以算法迭代次数为变量控制c1和c2的取值。在搜索初期，设置较大的c1和较小的c2，加强粒子对个体最优值的追随有助于提高搜索效率；在算法后期，粒子已基本找到最优分配方案，设置较小的c1和较大的c2，使粒子加强对全局最优值的追随以加快算法的收敛。因此，设计学习因子c1和c2随迭代次数服从半高斯分布，表达式分别如式（11）和式（12）所示。

其中，l 为迭代次数，NC为最大迭代次数，σ取值为最大迭代次数的1/4，设置学习因子c1和c2的取值范围在［Cmin，Cmax］区间内。

3.6 融入交叉和变异的粒子更新策略

为提高种群的多样性，避免算法陷入局部最优，在粒子迭代更新时，融入遗传算法的交叉和变异操作［23］。

在每次迭代计算出全局最优位置后，将其与随机粒子采用整数交叉法进行交叉操作［24］。首先选择两个交叉位置pos1 和pos2，将随机粒子pos1 和pos2 之间的片段用全局最优粒子pos1 和pos2 之间的片段替换，产生交叉粒子；对交叉粒子随机选择两个变异位置pos3和pos4，交换变异位置的粒子基因，即得到交叉变异后的新粒子；用新粒子随机替换群体中一个粒子。

3.7 加入罚函数的适应度函数

按照3.2 节所述的编码方式可自动满足2.2 节所述的约束条件2，但不一定满足约束条件1 和3，因此需要加入惩罚函数。算法的适应度函数如式（13）所示。

式中，F 为2.3 节式（5）所示的评价函数，该值越大，任务分配的收益越高。β、γ分别为违反时间窗约束和目标载荷约束的惩罚因子，lj为无人艇到达目标j 的时间，bj为目标j 的右时间窗，sj为对目标Tj最多可使用的载荷数。当无人艇到达目标的时间超过右时间窗时，需要给予时间惩罚，且超时越多，惩罚越大；当对目标使用的载荷数超量时，需要给予超限惩罚，且超出数量越多，惩罚越大。适应度函数等于评价函数减去惩罚函数，故适应度函数值越大越好。

4 算法流程

应用改进离散粒子群算法进行多无人艇任务分配的流程如图1所示。

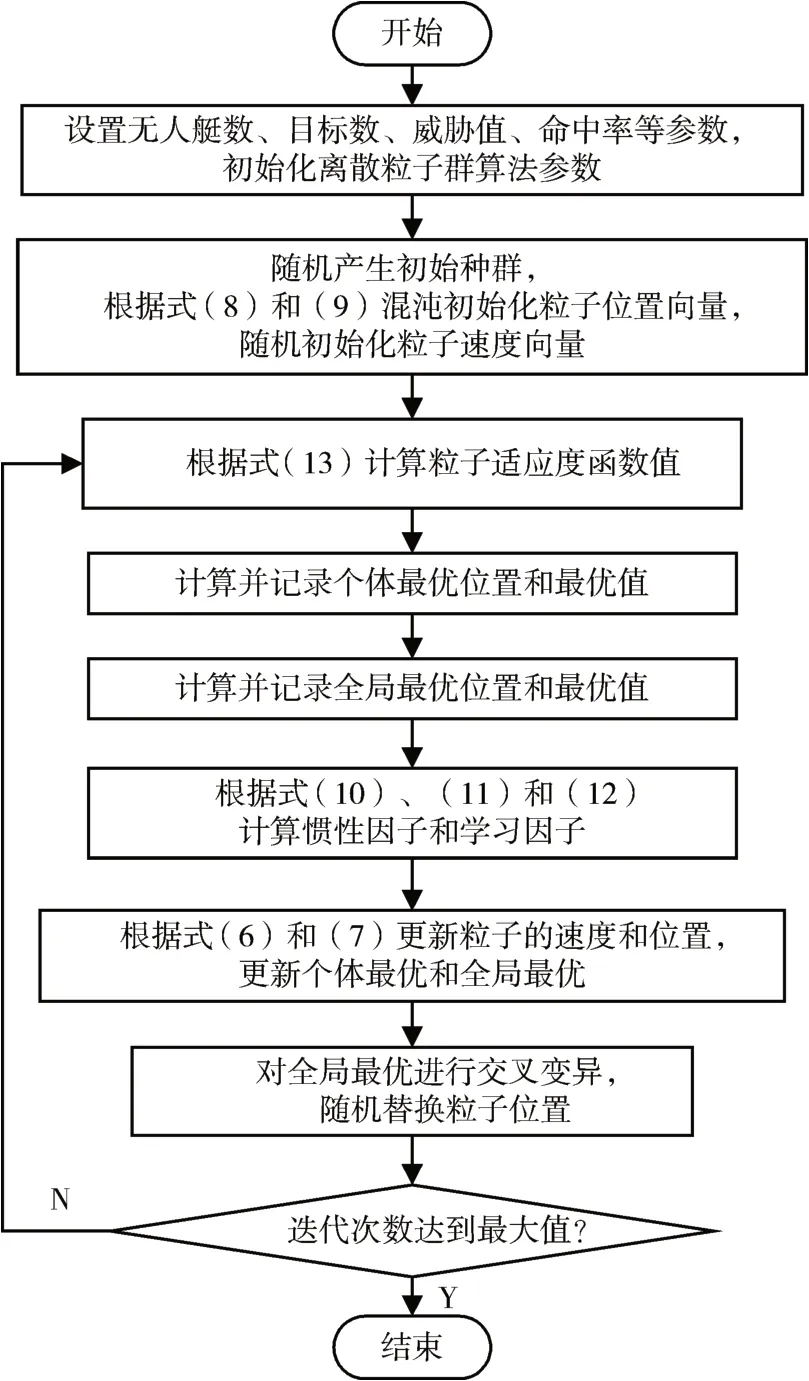
图1 改进离散粒子群算法流程图

5 仿真实验与结果分析

为检验本文提出的改进离散粒子群算法的有效性，进行如下仿真实验。设置粒子数量N 为40，最大迭代次数NC=200，权重因子最小值和最大值分别为0.4和0.8，学习因子最小值和最大值分别为1.2和1.5，无人艇数量为4，待打击目标数量为6，每艘无人艇搭载的载荷数量为2，无人艇航行速度为20km/h，根据适应度函数各组成部分的重要程度，同时均衡各参数的数值量级，设置ωR、ωD、ωT、β和γ分别为100、1、10、5、10，无人艇位置坐标如表1 所示，目标点位置坐标、威胁值、左时间窗和右时间窗如表2所示。无人艇对目标的命中概率如表3所示。

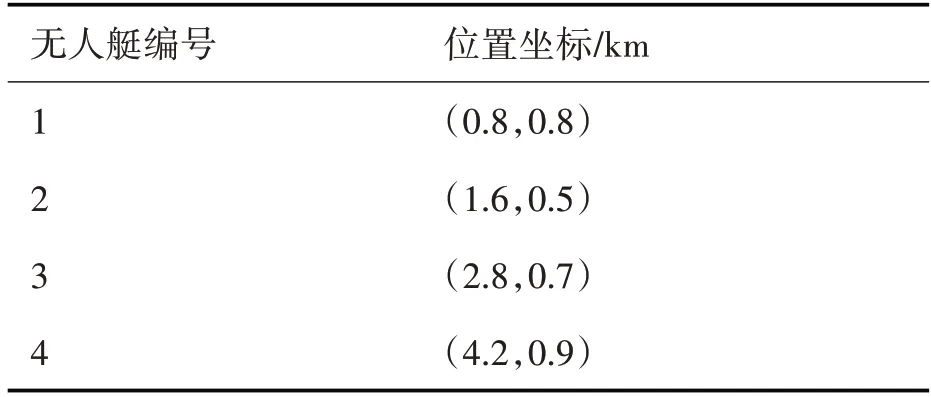
表1 无人艇位置坐标信息

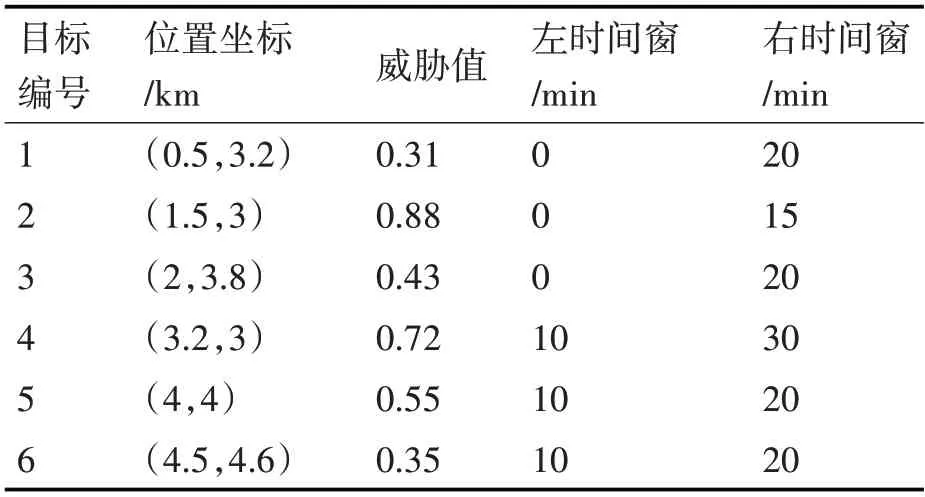
表2 目标位置坐标、威胁值、时间窗信息

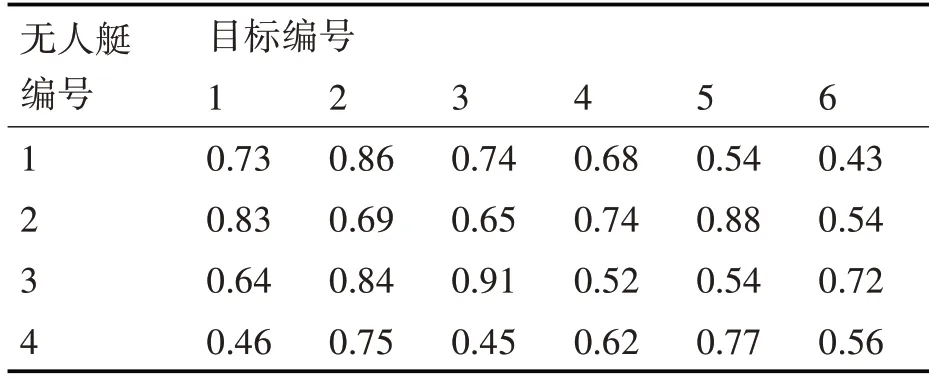
表3 无人艇对目标的命中概率

改进离散粒子群算法进行任务分配的结果如图2所示。

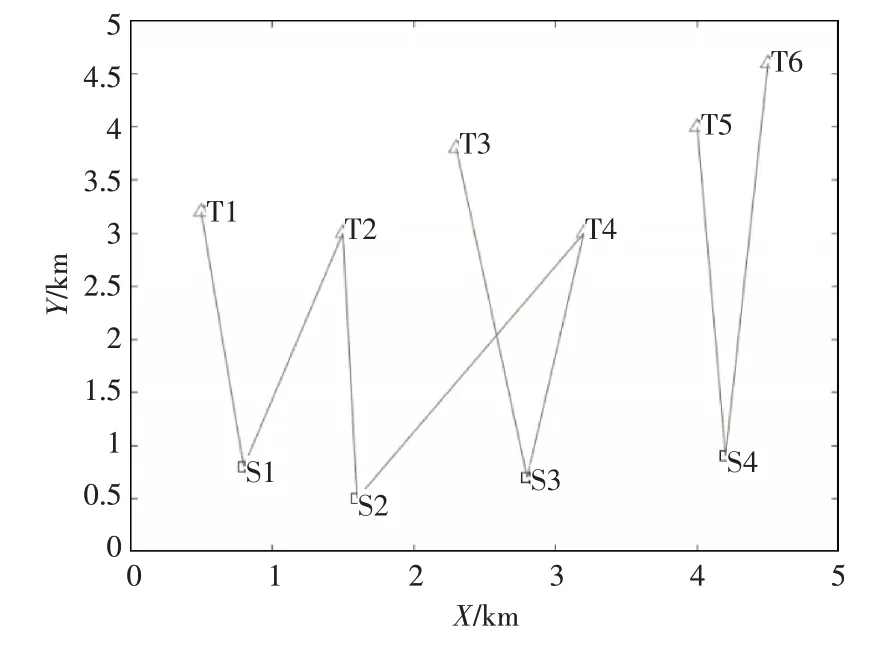
图2 改进离散粒子群算法任务分配图

传统算法和改进算法的任务分配适应度函数值随迭代次数变化的曲线如图3所示。

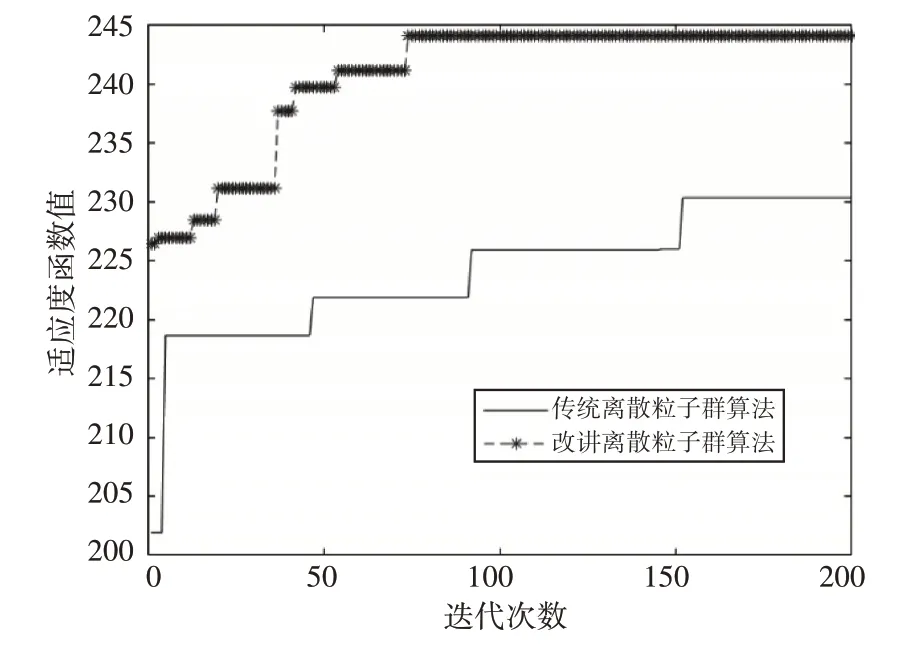
图3 传统算法和改进算法适应度函数值对比图

随机选取3 次实验，记录两种算法在适应度函数值、迭代次数和运行时间等方面的结果如表4 所示。

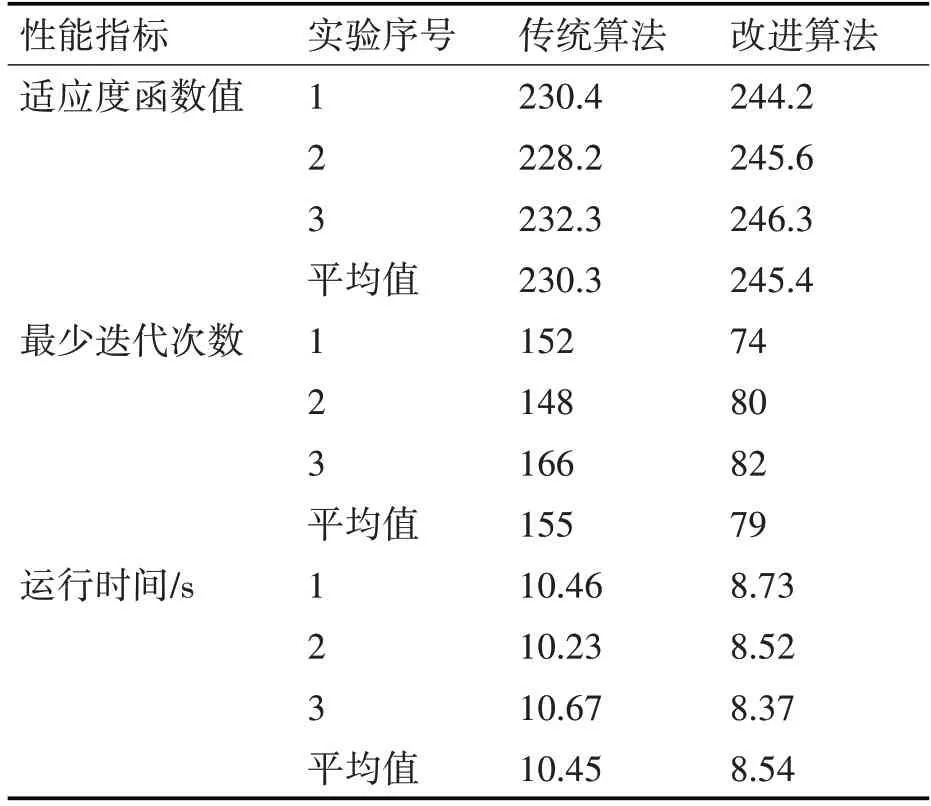
表4 传统算法和改进算法的性能对比

综上所述，与传统离散粒子群算法相比，改进后的算法具有较强的收敛性，整体迭代次数更少，规划的任务分配方案收益更高，这充分说明改进算法的优越性。

6 结语

本文采用改进的离散粒子群算法进行无人艇任务分配。为增强初代粒子群的多样性，提高算法的全局搜索能力，初始化粒子编码时融入混沌优化策略；设计随迭代次数呈指数递减变化的惯性因子，进一步提升搜索效率；设置服从半高斯分布的自适应学习因子c1和c2，以兼顾算法收敛速度快和全局搜索能力；融入交叉和变异的粒子更新机制，有效提高算法的全局搜索能力。仿真实验表明：改进后的算法具有较强的全局搜索能力，有效减小了迭代次数，较大程度提高了任务分配的质量。