基于点云数据的增材制造模型结构优化方法

薛 凯 郭润兰 黄晖阳 黄 华

兰州理工大学机电工程学院,兰州,730050

0 引言

机械结构的拓扑优化受到传统制造方式的限制往往难以实现,而增材制造技术的发展为拓扑优化结构的制备提供了强有力的支撑。但是,传统优化设计方法并未充分考虑增材制造技术引入新的工艺约束问题,表现为内部结构存在过长悬垂区域或结构角度过大。在悬空结构成形过程中, 要求当前层中的打印位置下方或附近必须有材料支撑,否则材料会因重力影响而发生掉落[1-3],无法保证正常成形,而且这些额外的支撑结构在成形结束后必须通过人工处理。

为了使具有悬垂特征的结构更好地成形,降低打印成本,提高打印效率,沈振宏等[4]提出了一种树形支撑结构算法,通过判断临界角来选择待支撑区域,然后构建一种树状支撑结构,在打印完成以后,使用特殊材料的结构会被特制材料消除掉,使其他结构不受影响。而LU等[5]则借鉴蜂窝结构思想,提出一种优化模型内部结构的新方法,在打印模型内部空间制作了类蜂窝状的单元,在保证打印模型满足一定物理强度的条件下,降低了打印材料的消耗。WANG等[6]提出一种基于蒙皮-刚架(skin-frame)的方法,在中空的打印模型内部使用细杆构建了一个稳定的支撑结构,从而使打印模型既节省材料又满足所需的物理强度要求。王继东等[7]采取对模型外表面进行偏移得到内表面从而挖空物体内部的方法,实现对内部结构的优化。徐洪飞等[8]通过体素化的方式建立基于应力分布的壳模型和构造优化算法,形成非均匀厚度的壳模型。上述结构优化方法均得到了较好的成形结果,但是对成形过程中因为结构改变额外生成的支撑结构缺乏考量。

针对成形过程中产生支撑的问题,桂馨[9]提出了一种基于固体各向同性材料惩罚模型(SIMP)法和能量均匀化法的自支撑结构多尺度拓扑优化,在宏观结构优化阶段,利用SIMP法获取自由分布的宏观材料空间,在微结构设计阶段,进行自支撑微结构设计,最终获得自支撑结构。WANG等[10]提出了一种基于分层过滤策略的SIMP改进方法和一种基于悬垂灵敏度分析的双向渐进结构拓扑优化(BESO)改进方法,以减少优化设计中悬垂结构的产生,从而避免产生支撑结构。ZOU等[11]提出了一种基于max/min函数识别非自支撑单元,通过不等式约束控制非自支撑单元数量,得到自支撑结构的方法。EMIEL等[12]将设计域分层,以设计域内每个点材料到达时间为判断依据判断支撑性,优化设计自支撑结构。LEE等[13]在模型内部建立按照一定方式排列的椭球结构来实现内部的结构优化,在一定程度上实现内部结构的自支撑。

不同的结构优化方法有着相同的目标,都是在满足一定边界条件下,使模型成形效率更高,成本更低。这些内部结构优化方法在成形质量及强度质量比两个维度上有一定提升,但是在形成独特的内部结构过程中,因为增材制造工艺特点,仍然不可避免地生成额外的支撑,比如蜂窝结构中一些接近水平的蜂窝顶部,桁架结构中顶部及其他位置横置的一些杆。如果成形过程中不对其加以支撑,该处结构会因重力作用产生塌陷,甚至破坏整体成形结果。

针对上述问题,本文提出一种内部结构优化方法,在提出模型结构优化方法的同时,满足成形过程中内部结构实现自支撑的要求,使模型成形过程中无需多余的支撑结构。首先利用点云数据方法获得模型轮廓特征数据,然后将不同特征部分进行分割,从而建立与特征匹配的内部孔洞,在内部重新构造自支撑结构以避免成形过程中产生额外支撑。

1 点云数据处理

本实验通过PCL(point cloud library)库中点云转化代码,将三维模型转化为方便处理的三维点云格式文件,利用无序点云数据方法获得三维模型轮廓数据,然后根据其不同部位特征将其分割,实现点云格式模型特征分离。在此基础上,在点云格式文件里提取各个部分的关键点,利用空间最小二乘法拟合关键点,得到与外部特征相匹配的内部椭球孔洞,对孔洞大小、位姿进行调整,以符合增材制造成形特点。

1.1 模型特征分离

点云数据区域分割方法是根据空间、几何、纹理等特征对点云数据进行划分,文中依据曲率对模型点云数据进行判断,将一定范围内小于曲率阈值的点云划分在同一区域。实验中采取基于区域生长的分割方式,对模型不同特征进行分割。

对数字模型进行分割处理,输出的是几个聚类集合,每个聚类集合被认为是同一光滑表面的一部分。区域生长算法是从曲率最小的点开始生长的,所以依据数字模型点的曲率值对点进行排序。得到的曲率最小的点设置为初始种子点,此时初始种子点所在的区域即为最平滑的区域,一般数字模型中平面区域较大,这样从最平滑的区域开始生长可减少分割区域的总数,提高分割效率。

设置一个空的种子点序列和空的聚类数组,选好初始种子点后,将其加入种子点序列中,并搜索邻域点。对每一个邻域点,比较邻域点的法线与当前种子点的法线之间的夹角,小于平滑阈值的邻域点加入当前区域。检查每一个邻域点的曲率值,小于曲率阈值的邻域点加入种子点序列中。判断初始种子点(图1中A点)与第一个邻域点(图1中B点)法向量夹角β<35°,然后判断其曲率值大于0.05,所以排除该点,继续寻找下一个邻域点(图1中C点),该点法向量夹角α<35°,曲率值小于0.05,所以该点加入种子点序列。本文中所取参数值均为对模型多次实验取得的最佳效果值。

图1 区域生长原理图

在进行种子点邻域判断后,删除当前种子点,利用新加入的种子点继续生长,重复进行以上生长过程,直到种子点序列被清空。一个区域生长完成,将其加入聚类数组。最后,利用曲率值从小到大排序,顺序选择输入点集的点作为种子点加入种子点序列中。重复以上生长的步骤,这样就通过区域生长方法实现了点云数据的分割。在分割过程中,需要不断调整分割参数,以达到更好的分割结果。

本次实验中,表1所示的分割参数为实际参数,其中KN为用于法向量估计的k近邻数目,BC表示是否需要直通滤波,FC为直通滤波的最大值,NC为直通滤波的最小值,ST为平滑阈值,CT为曲率阈值。图2给出了点云分割示例,点云处理结果如图2c所示,不同颜色区域代表分割的不同部分。可以看到,分割结果很完整,不同特征分割位置很明确,说明了区域生长分割方法的有效性。

(a)数字模型 (b)点云数据 (c)点云分割 (d)关键点提取图2 Bunny模型处理过程

表1 分割参数

1.2 关键点提取

关键点也称为兴趣点,它是可以通过定义检测标准来获取的具有稳定性、区别性的点集。关键点的数量相比于原始点云或图像的数据量小很多,它与特征描述子结合在一起,组成关键点描述子,常用来形成原始数据的紧凑表示。尺度不变特征转换 (scale-invariant feature transform,SIFT)[14]是一种具有尺度不变性的局部特征描述子。SIFT能够找出不会受移动、转动、缩放、仿射变换等外在因素的影响而改变其特性的关键点,对于具有明显特征的点云数据来说,利用该方法可以快速找到模型特征关键点。

完成对模型的分割以后,寻找模型各特征部分的关键点,文中采用SIFT关键点提取方法对各个特征部分点云数据提取关键点,其中,尺度空间中最小尺度的标准偏差设置为2,高斯金字塔组(octave)的数目设置为6,每组高斯金字塔组计算的尺度为4,限制关键点检测的阈值为0.01。对分割后的各个模型进行处理,由SIFT方法提取各特征部分的关键点。由图2d可知,Bunny模型关键点呈均匀分布状态,上部、下部关键点数量与其特征大小相关,该结果与模型分割结果具有一致性,说明模型分割处理及其关键点的提取符合模型特征。

1.3 生成椭球孔洞

椭球体具有良好的力学性能,它的光滑边界能够显著减小应力集中的情况[15],所以椭球体特征经常出现在对质量和力学性能有要求的结构中。而且椭球体的形状参数调整选择更丰富,因此本文中模型内部结构选择椭球结构。成形过程中选择合理的椭球结构参数能够对实体模型产生更好的支撑,保证实体模型的力学性能。

得到模型点云数据不同部分的关键点后,以模型几何结构特征为约束,过滤各模型中相对体积较小的特征,只保留特征尺寸明显的部分。比如选择Bunny模型的头部和腹部作为优化重点,忽略耳朵及脚部特征。在三维空间内将坐标点代入椭球公式计算,获得与各特征部分相匹配的椭球参数。此时获得的椭球结构是超出模型点云数据边界的,因为关键点的选取在模型边界上,所得椭球结构大小在与初始模型配准时需要调整。

利用最小二乘法对得到的关键点数据进行拟合,椭球空间二次曲面标准表达式为

(1)

其中,x0、y0、z0为椭球中心坐标;m、n、l分别为椭球半轴长。

假设椭球中心为原点,那么式(1)可以写成

(2)

将关键点三维坐标输入空间椭球拟合代码中,输出拟合完成后的椭球参数。

为了使得到的椭球与模型特征匹配,在得到椭球形状后,需要确定椭球结构在模型内部的位姿,防止其超出模型边界,造成模型结构失效。此时利用点云数据配准方法确定椭球在模型内部的位置姿态。点云配准将从各个视角得到的点集合并到一个统一的坐标系下,利用输入矩阵来实现点云数据的移位。文中采取4点全等集配准算法[16]实现椭球结构与模型的配准。该算法的核心思想就是利用刚体变换中的几何不变性,即刚性变换后交点所占线段比例不变以及点之间的欧氏距离不变,在目标点云中尽可能寻找4个近似共面点与之对应,从而计算得到变换矩阵。

如图3所示,在点云数据中选取共面的4个点,连接ab、cd交于e点,r1、r2分别为端点和交点距离与线段的比率,r1=‖a-e‖/‖a-b‖,r2=‖c-e‖/‖c-d‖,提取r1、r2,保证比率不变的情况下,在给定共面点集中寻找与其相近的点。对点集P中的点两两配对,寻找其交点,如果e1≈e2,则{a,b,c,d}与{q5,q3,q4,q1}两个点集相似,可以输出变换矩阵。配准过程中,需在清晰的关键点特征描述下才能保证后续流程中的变换矩阵估计的准确性和效率。

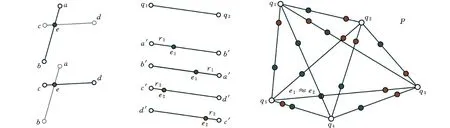
图3 4点全等集原理图

配准结果如图4所示。4点全等集配准算法得到的结果,椭球结构所处位置距上下边界保留充足距离,避免了在模型一些结构特殊位置产生干涉,甚至影响模型的结构;而两两配准法得到的结果,椭球结构与模型特征产生明显干涉,且椭球结构与预想位置偏离很大。

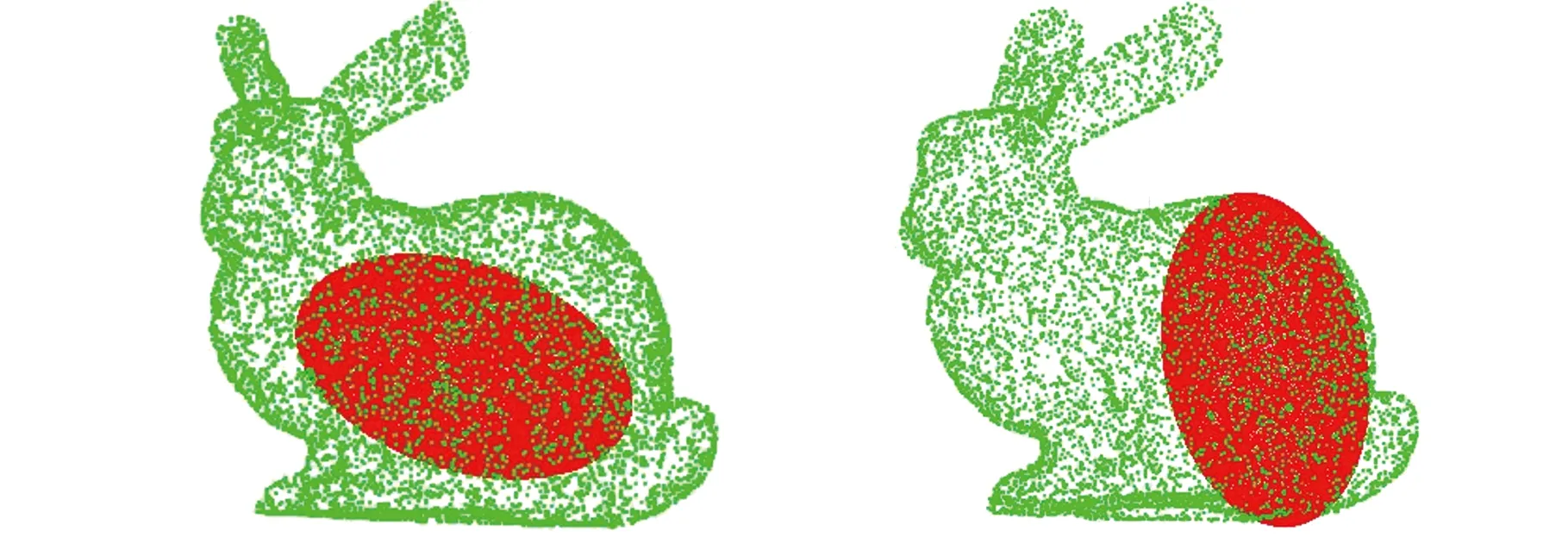
(a)4点全等集配准 (b)两两配准

完成椭球结构与模型配准以后,将所得点云数据通过Geomagic Design X软件处理得到数字模型。当椭球结构缩放为初始大小的85%时,在Bunny模型腹部与腿相交处,椭球结构与模型之间距离较近,如果继续用该模型成形为实体模型,很难保证该处结构不会发生破坏,如图5a所示。经过多次试验,当缩放比例为70%时,能在保留足够壁厚的情况下,达到椭球结构的最大化,保证了结构优化的效率,如图5b所示。

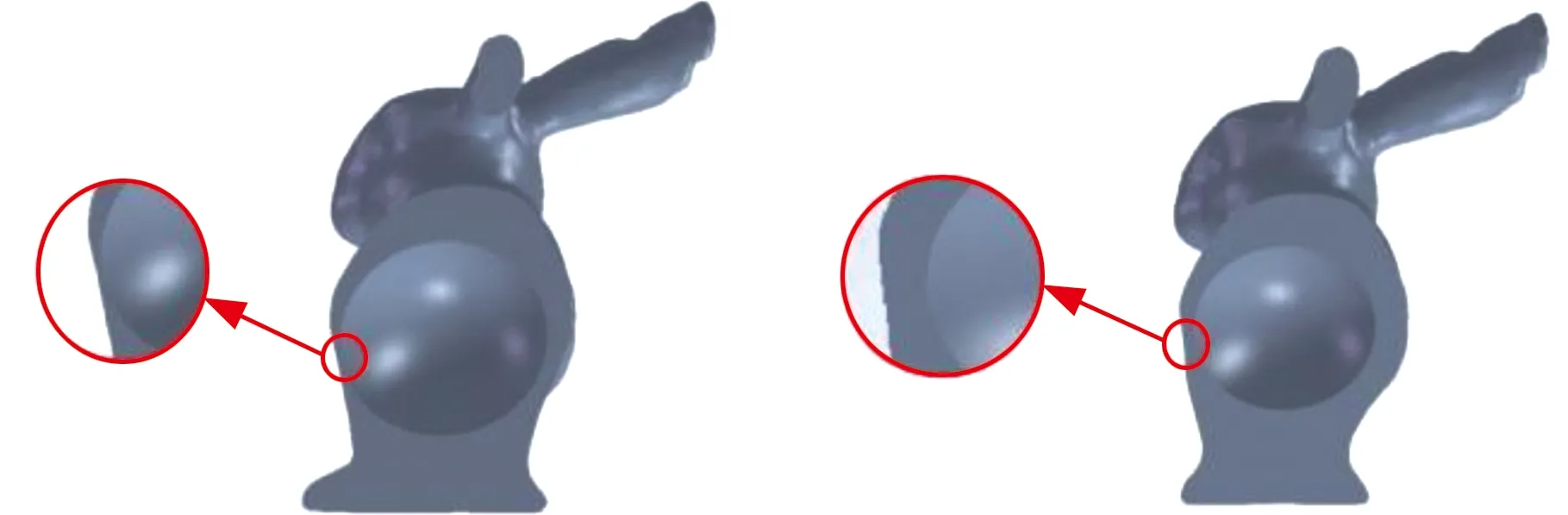
(a)85%椭球大小 (b)70%椭球大小

2 自支撑结构

2.1 封闭孔洞识别

将模型放置为水平打印角度,识别其待支撑区域,本文中主要针对内部掏空部分生成支撑结构,所以识别区域为封闭椭球部分。参考LUO等[17]提出的非线性虚拟温度法,将孔洞部分假设填充为一种自加热的高导热材料(热导率k和热流密度q设置为较大值),将结构实体部分设为绝热材料(为避免热问题有限元分析奇异性,k设为一个较小值,q为0),求解散热边界下的虚拟温度场问题。

利用外部温度场的变化来判断是否为封闭孔洞,当外部温度升高时,说明存在未封闭孔洞;当识别到模型内部温度升高时,说明有封闭孔洞存在。通过虚拟温度场识别模型内部的封闭孔洞,然后在封闭孔洞部分构造对称式自支撑结构,保证模型结构强度,如图6所示。

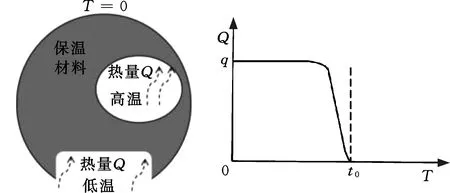
(a)封闭孔洞原理图 (b)温度场变化图

2.2 对称式自支撑结构

本研究采用长椭球体作为优化目标,但是不同模型特征对应椭球孔洞大小不同,而支撑结构尺寸与椭球孔洞尺寸相关。假设Z轴平行轴为最长轴,打印方向平行于Z轴,长椭球体通过围绕其长轴旋转椭圆得到。如图7所示,在OXZ平面上,假设p1、p2为椭圆上的点,其中切线对应θ0,此时,在椭球上半圆其他p1p2大于ɑ0的位置可以直接成形,无需多余的支撑结构。如果p1p2小于45°,此时θ0大于45°,那么红色圆弧部分在成形过程中无法单纯依靠材料自身黏结性直接成形,在其下方需要多余支撑结构,否则会产生塌陷。为此,在识别到封闭孔洞区域后,在封闭孔洞内部建立自支撑结构来实现椭球孔洞的完整成形。

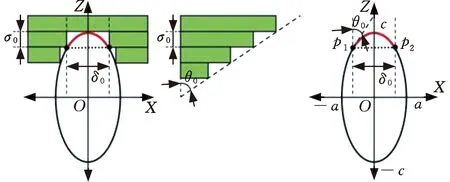
图7 支撑倾角示意图

三维打印系统多用STL格式文件表示零件的数据,因此用三角面片近似整个零件的表面。通过三角面片法向量与Z轴负方向夹角θ与临界值β大小获取所需支撑面片信息。θ≥β时,由于材料自身的黏结作用,无需添加辅助支撑结构;θ<β时,需要对面片添加支撑,同时对向下倾斜且不需要支撑区域的局部最低的点和线段进行识别。对于识别的待支撑面片集合Tsup,需要将集合中共边的面片进行合并,得到若干独立的待支撑区域A0,A1,…,An:

(3)

i,j=1,2,…,n且i≠j

面片合并结果如图8所示。

图8 待支撑面片集合Tsup

将相邻的离散三角面片进行整合作为待支撑区域后,从待支撑区域向下投影,得到对应底层支撑生成区域,从上、下待支撑区域分别生成支撑结构。首先获得区域投影的投影面,然后对待支撑区域进行栅格划分,在投影区域内采样一系列的待支撑点,采用一定的栅格间距d对待支撑区域进行网格划分。栅格间距d的选取与材料的临界打印长度(材料在没有支撑的情况下保持不变形的极限打印长度)L有关。为了保证支撑的稳定性,同时避免选择的支撑点过于密集,选取经验值d=L/2。从栅格的左下顶点开始,逐行往上判断每个栅格中的顶点个数。当栅格中的点个数为0时,插入相应的点并保存;当栅格中的点个数大于1时,计算这些点的中心点并保存。此时,由上方待支撑区域开始向下生成支撑,对待支撑区域划分网格,如图9所示。为了避免支撑结构不足,对其中所有节点进行包络操作,以节点包络圆作为支撑结构边界,以保证支撑强度。

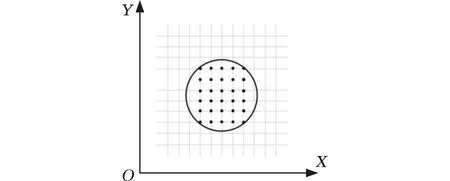
图9 节点包络图

如图10所示,产生首层支撑轮廓以后,判断顶层与底层之间距离H,按层厚将首层轮廓线向下偏移h(h为层厚),对于待支撑点集P中的点p0,假设通过下方的点s1进行支撑,则s1p0与加工方向的夹角不大于临界倾角β。以首层轮廓节点为原点,将该层包络线向轮廓中心以β角发射射线,与下层的交点p即为下层节点,连接最外圈节点即为下层轮廓圆,逐层计算。投影高度H的中间位置为中心层,该层轮廓圆为最小轮廓圆。底层待支撑区域与上方支撑生成方式相同,方向相反。向上偏移h,直到与中心层支撑轮廓相交。得到对称式结构后,将带有支撑结构的模型转化为可打印的STL文件,经后续分层处理得到模型的切片数据,然后再进行路径规划,从而完成模型的打印。

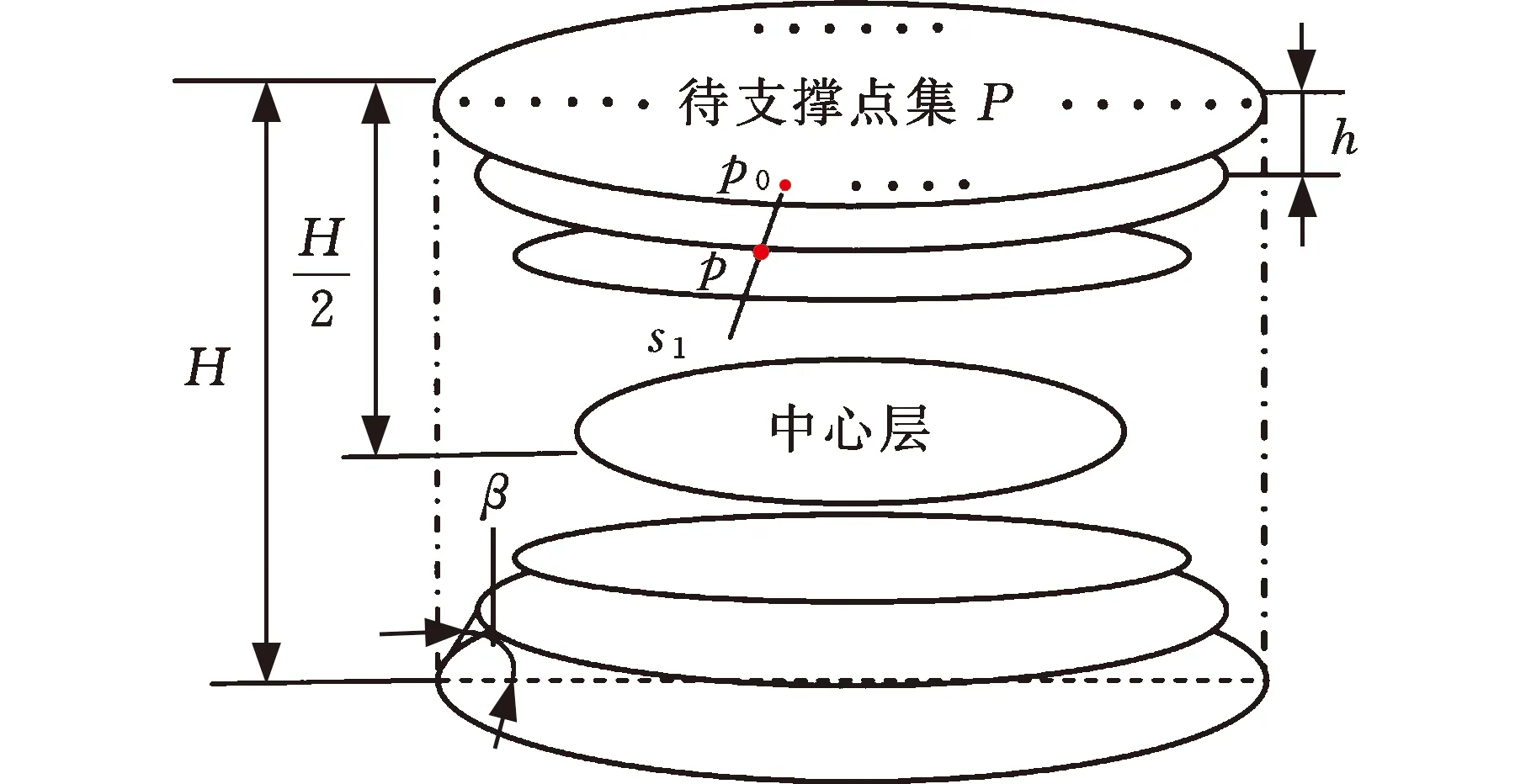
图10 支撑生成原理图

通过分层保存的节点轮廓信息,使用水平截面单元逐层扫掠各层节点到其子节点的路径,获得初始曲面顶点,然后对这些顶点进行处理,生成网格曲面,最终生成支撑结构。

3 模型切片

将优化后的猫模型输入Cura切片软件,打印材料设置为PLA,密度为1240 kg/m3,弹性模量为3.5 GPa,泊松比为0.36,填充图案设置为网格填充,填充率设置为25%,层厚设置为0.2 mm,模型壁厚设置为1 mm。对原始猫模型和优化后的猫模型进行切片,得到内部支撑数据如图11所示,该层切片为第42层切片数据。在原始模型切片中(图11a),内部均匀分布着网格支撑;而优化后模型中(图11b),在生成椭球孔洞处,对称式支撑结构完成了对内部结构的支撑,没有产生额外的支撑结构。

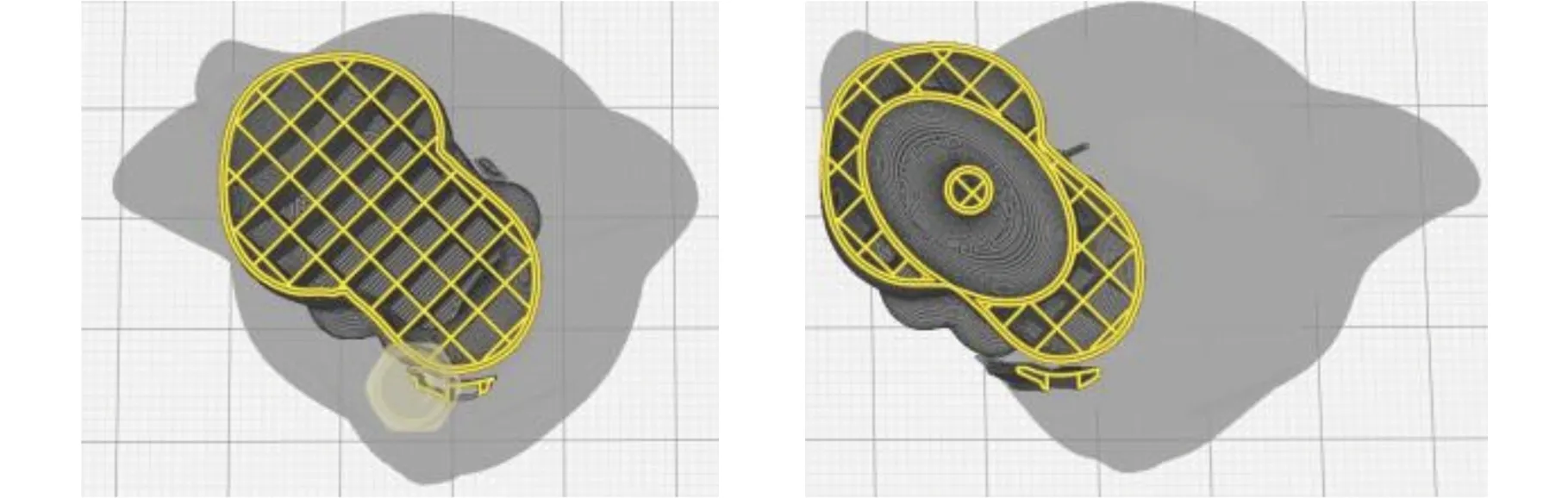
(a)优化前切片 (b)优化后切片

4 成形实验

在完成模型的优化以后,使用商用FDM 3D打印机极光尔沃A6制作模型,打印尺寸为300 mm×200 mm×200 mm。打印机的可打印精度范围为0.1～0.4 mm,打印层厚h设定为0.2 mm。打印中使用塑料PLA材料,并将最大允许悬垂角度设置为45°,可打印水平悬挂的最大长度为5 mm。在成形过程中为模型的外部添加支撑结构,在模型内部不添加任何支撑。模型制作完成后,手动移除外部支架。

打印的模型如图12所示,通过模型分解可以看到模型内部的对称式自支撑结构的完整切面。对称式自支撑结构直接成形,在模型内部没有产生多余的支撑结构。利用本文提出算法优化的模型与常规模型结构相比,在打印时间和材料消耗方面均有明显改善,如表2所示。在实验中,时间最高缩短25%,材料消耗最高减少20%。平均打印时间减少16.4%,打印材料消耗减少12%。在保证成功成形的前提下,提高了打印效率,降低了打印成本。本文方法对特征较多的模型优化效果尤其显著。以猫模型与Bunny模型为例,两个模型具有明显球类特征,在其内部形成椭球结构时计算量更小,在最终成形效果上表现为内部椭球结构更明显,在时间、材料消耗方面优化效果更显著。

表2 成形结果对比

(a)猫 (b)Bunny

5 结论

(1)内部优化结构成形过程中如无法满足自支撑要求,易在生成内部结构的同时生成不必要的额外支撑结构。为此,本文以模型几何结构特征为基础,提出了一种结构优化方法,在对模型内部结构优化的同时,生成对应的内部自支撑结构。

(2)利用点云数据处理方法对模型进行处理,选择椭球结构作为内部结构优化目标,针对不同模型不同特征,在实体模型中成功建立一个或多个椭球结构,每部分椭球结构与外部特征相对应,实现了内部结构的精准优化。在保证完整成形结果的情况下,提高了打印效率,降低了打印成本。

(3)提出一种对称式自支撑结构生成算法,在识别模型内部封闭孔洞需要支撑结构位置之后,在其内部建立对称式自支撑结构。该结构满足自支撑条件,无需在内部产生额外支撑结构,降低了后期处理的难度。