基于改进灰狼算法优化ELM的边坡稳定性评价

马艳梅,毕晓茜

(1.淮南职业技术学院,安徽 淮南,232001; 2.徐州工程学院,江苏 徐州 221018)

0 引言

边坡的稳定性问题是边坡研究的核心,在人类的许多工程活动中,对边坡稳定性评估得准确与否将会对人们的人身和财产的安全产生重要影响[1]。依据《中国统计年鉴》汇总,2016年这一年中,我国就出现了9710次地质灾害,不同灾害比例图如图1所示。由图1可知,滑坡灾害约占76%,因此对边坡稳定性进行准确的评估具有重要的现实意义[2]。

图1 不同灾害比例图

边坡是一个非常复杂的系统,其稳定性受到多种因素的制约,且存在较大的随机性,非常不容易准确判定其是否稳定。当前,边坡稳定性评价的方法主要有极限平衡法、灰色关联法、支持向量机、神经网络、判别分析和极限学习机等[3-7]。这些方法虽然取得了一定效果,但是均存在一定的局限性,诸如精度不高、训练时间长和局部最优等问题。为了提高边坡稳定性评价的精度,本文提出一种改进的灰狼算法(Improved Grey Wolf Optimization Algorithm,IGWO)优化极限学习机的边坡稳定性评估方法。

1 改进的GWO算法

由于GWO算法的初始种群是随机生成的,在求解区域中,原始群体的不均匀分布,不能完全涵盖全局,从而对GWO算法的搜索速度产生一定的限制。为了改善GWO的初始群体的一致性和多样性,应用反向学习方式对GWO进行初始化计算。

在GWO算法中,收敛系数a是由2向0逐渐减小的,因此在GWO算法的初始阶段,它的收敛性是最小的。a具有更大的数值,以进行全局搜索;GWO的数值随GWO迭代数的增大而降低,从而实现了局部精确查找。为了增强全局最优化方法的搜索性能,文中给出了一种基于一个非线性收敛性系数的修正方法[12]:

(1)

式中Tmax和t分别为最大迭代次数和当前迭代次数。

2 基于IGWO-ELM的边坡稳定性评价模型

2.1 极限学习机

极限学习机(Extreme Learning Machine,ELM)具有结构简单、训练速度快的优点,是一种单隐含层的前馈神经网络,其模型结构如图2所示。

图2 ELM模型结构图

对于N个训练样本(Xi,Ti),输入变量Xi=[xi1,xi2,…,xin]T∈Rn,输出变量Ti=[ti1,ti2,…,tim]T∈Rm,其中输入变量的数量和输出变量的数量分别为n个和m个。因此,隐含层节点数为L的ELM模型为[13]

(2)

式中Wi=[wi1,wi2,…,win]T为输入权重,βi为输出权重,g(x)为激励函数,Wi·Xj为Wi和Xj的内积,bi为第i个隐含层节点的偏置。

ELM模型训练的目标就是确保式(3)的误差最小。

(3)

由式(2)和式(3)可知,存在一组βi、Wi和bi满足(4):

(4)

式(4)可以写成矩阵的形式:

Hβ=T,

(5)

式中H为隐含层的输出矩阵,β为输出权重矩阵。

H矩阵、β矩阵和T矩阵可以用式(6)表示:

H(W1,…,WL,b1,…,bL,X1,…,XL)=

(6)

式中的上角标T为矩阵的转置操作。

(7)

因此,求解式(8)可以得到β的最小二乘解:

(8)

(9)

2.2 目标函数

由ELM基本原理可知,ELM模型的输入层权值矩阵和隐含层偏置矩阵是随机初始化产生的,因此ELM方法的计算结果具有很好的稳定性和准确性。为了改善 ELM的建模效果,利用 IGWO算法优化ELM的输入层权重和隐含层偏压矩阵,找到最优ELM模型。选择均方根误差(RMSE)作为IGWO-ELM的目标函数:

(10)

式中N为训练样本的个数,Ypi和Yi分别为第i个训练样本的ELM模型预测值和真实值。

2.3 算法流程

影响边坡稳定性的因素有很多,如黏聚力、内摩擦角和节理面等。根据文献[14-15]收集的露天矿边坡评价实例,本文选取重度、黏聚力、摩擦角、边坡角和坡高5个指标作为边坡稳定性评价的指标。基于IGWO-ELM的边坡稳定性评价流程如图3所示。

基于IGWO-ELM的边坡稳定性评价算法流程可描述为

1)读取边坡稳定性评价影响因素数据(重度、黏聚力、摩擦角、边坡角、坡高以及安全系数),划分培训集合和测试集合,并使之规范化:

(11)

式中x′为归一化之后的数据,a、b为归一化之后的最小值和最大值,x、xmax和xmin分别原始数据、原始数据中的最大值和最小值。

2)对各灰狼的适应度fi进行了分类,将适应度最高的3只灰狼种的位置记录下来,分别记作为Xα、Xβ和Xδ。

图3 基于IGWO-ELM的边坡稳定性评价流程

3)更新参数a、A和C。

4)判断方法终止条件:在最大迭代数Maxgen下,最优的输出ELM模型的输入层权重和隐含层偏压,反之,则回到第3步。

5)在ELM模式中引入最优输入层权重和隐含层偏差进行边坡稳定性评价。

3 工程实例分析

3.1 数据来源

传统的边坡稳定极限平衡方法是以莫尔-库仑屈服准则为基础,以滑动面上的剪切强度与真实剪切力之比来确定安全系数,并以此为基础,通过理论推导得出:

(12)

式中c为黏聚力,φ为摩擦角,σ为边坡角,τ为重度,l为坡高。

为了验证应用IGWO-ELM进行边坡稳定性评价的有效性,选择文献[16]中的露天矿边坡评价实例为研究对象,样本数据见表1,一共27组。将边坡样本数据划分为训练集与测试集,其中训练集22组,测试集5组。重度、黏聚力、摩擦角、边坡角和坡高为IGWO-ELM的输入值,安全系数为IGWO-ELM的输出值。训练集用于建立IGWO-ELM模型,测试集用于验证IGWO-ELM模型的正确性。

表1 边坡样本数据

3.2 结果分析

为了说明IGWO-ELM的优势,将IGWO-ELM与GWO-ELM、PSO-ELM和ELM进行对比。不同算法的参数设置:1)ELM参数为输入层神经元个数N1=5,隐含层神经元个数N2=10,输出层神经个数N3=1;2)粒子群算法(PSO)的参数为人口数量N=10,最大迭代数为100,学习因子c1=c2=2,搜索区间[-1,1];3)IGWO和GWO的参数为群体大小N=10,迭代最大个数为100。不同算法收敛曲线如图4所示,训练结果如图5所示,预测结果如图6和表2所示。

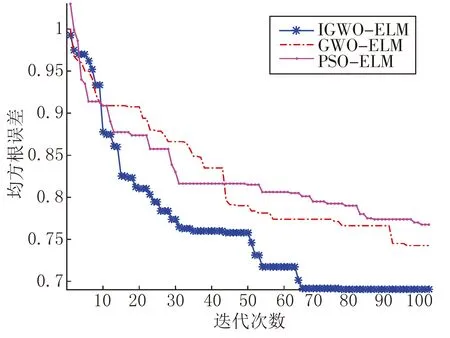
图4 收敛速度对比图

由图4可知,与GWO-ELM和PSO-ELM相比,应用IGWO-ELM进行边坡稳定性评价具有更快的收敛速度和更小的适应度。主要因为反向学习策略提高了种群的多样性和均匀性,此外非线性收敛提高了GWO算法的收敛速度。

图5 训练结果

图6 预测结果

表2 测试集预测结果对比

由图6和表2可知,与ELM、PSO-ELM、GWO-ELM相比,应用IGWO-ELM进行边坡稳定性评价具有更高的精度,其平均绝对相对误差为5.55%,优于GWO-ELM的10.37%,PSO-ELM的11.23%和ELM的23.57%,从而证明了应用IGWO-ELM进行边坡稳定性评价的有效性。通过对比发现,经过PSO、GWO和IGWO等智能算法的优化,各ELM的评价精度均有了较大程度的提高,主要因为智能算法对ELM的输入权值矩阵和隐含层偏置矩阵进行优化选择,提高了模型精度。但是对边坡稳定性的影响因素只选择了重度、黏聚力、摩擦角、边坡角和坡高等,未考虑地下水、软弱结构面等因素的影响,因此导致部分样本的稳定系数评价误差较大,具有较大局限性,后续将综合考虑影响边坡稳定性的相关系数,提高模型的适用性和可靠性。

4 结论

本文采用逆向学习的方法,结合非线性收敛因素,对传统的GWO算法进行了改进,提高了标准GWO算法的种群多样性和分布均匀性以及收敛速度,将改进的GWO算法用来优化ELM模型的输入权值矩阵和隐含层偏置矩阵,并进行了边坡稳定性评价。研究结果表明,与ELM、PSO-ELM和GWO-ELM相比,应用IGWO-ELM进行边坡稳定性评价精度更高,具有一定的工程应用价值和推广价值。