固体火箭发动机尾焰中颗粒速度的粒子轨迹法测量①

相恒升,程 博,张成飞,乔文生,徐海涛

(1.清华大学 能源与动力工程系及燃烧能源中心,北京 100084; 2.内蒙航天动力机械测试所,呼和浩特 010010;3.清华大学 航天航空学院及燃烧能源中心,北京 100084)

0 引言

导弹及某些空间飞行器多使用具有特定性能的复合固体推进剂,使用这类推进剂时一般会在其中加入金属或非金属颗粒以提高推进剂的比冲以及抑制震荡燃烧[1-3]。然而,添加金属或非金属颗粒也会带来一些不利影响:推进剂燃烧产生的凝聚相燃烧产物导致发动机出现两相流损失[4-5];金属颗粒也会加重射流对喷管的侵蚀[6-9],如 1993 年美国 Titan IV 运载火箭因为颗粒对喷管的侵蚀在点火后约 100 s发生了爆炸[10]。发动机尾焰中颗粒速度的实测数据可以用来验证固体火箭发动机中两相流的理论分析和数值计算[11],为新一代发动机能量损失模型构建提供数据支撑。因为颗粒惯性正比于粒径的平方,大颗粒的惯性更大,所以大颗粒对于喷管的侵蚀作用也更明显。此外,发动机尾焰流场中存在激波引起的气流速度突变,这种突变对小颗粒和大颗粒的影响也可能完全不同。因此,测量尾焰中大尺寸颗粒的速度对于正确认识发动机尾焰流动具有重要的实际意义。

然而,测量固体火箭发动机尾焰中的颗粒速度存在诸多困难,主要体现在以下几点:(1)流场温度高,固体火箭发动机尾焰中的温度超过2000 K[12-13];(2)尾焰流场速度高[14];(3)尾焰中颗粒浓密[15];(4)火箭发动机尾焰为超音速气流并伴有强烈的温度及压强变化,尾焰流场中气体密度变化较大[16],并且尾焰边缘存在强烈的密度梯度,这导致的折射率变化使得经过尾焰的光线发生复杂的偏转。这些因素给发动机尾焰测量带来了很大困难,目前能够测量的固体火箭发动机内外流场参数比较少,几乎只能测量发动机推力曲线和发动机前端压力随时间变化的曲线[16]。发动机尾焰中颗粒速度测量受制于这些困难[17-18],常见的粒子速度测量技术,如PIV、LDA、LTV等难以应用到真实固体火箭发动机尾焰流场中颗粒速度的测量[19]。PIV虽然可以实现全场颗粒速度测量,但在发动机尾焰中因颗粒数密度高PIV将失效;LDA因为入射激光经过高温尾焰后产生不可控制的偏转而无法形成测量区,导致LDA无法测量;LTV的测量区域每次只能有一个颗粒,同样因为尾焰中颗粒浓密导致该技术失效。此外,发动机尾焰中高温辐射对LTV是强烈的信号噪音,这也将会导致LTV无法测量。

鉴于固体火箭发动机尾焰中颗粒速度测量比较困难,发动机尾焰中颗粒速度测量的相关文献比较少。PAGLIAROLI等[14]利用两个光电探头采集尾焰中颗粒散射信号,通过对两个信号做条件互相关计算得到颗粒通过两个光电探头探测区所用时间,两光电探头探测区间距已知,可求得颗粒速度。BALAKUMAR与ADRIAN[16]利用 PIV 技术测量了喷喉直径为 2.7 mm 的模型固体火箭发动机尾焰流场,流场中最高速度为 630 m/s。SAILE等[17]利用 PIV 技术对一系列不同喷喉直径(喷喉直径分别为 7.75、6.75、5.74 mm)、使用不同配方推进剂及不同燃烧室压力的缩比固体火箭发动机尾焰流场进行了测量,PIV 测量区域约为 30 mm×30 mm,实验发现,即使对如此小尺寸的发动机进行 PIV 尾焰流场测量,对某些工况(推进剂 HTPB1814),PIV 测量仍然会失败,作者将 PIV 测量失败的原因归结为流场中颗粒浓度太高及背景辐射太强。

由于尾焰中大颗粒的辐射强度也远高于小颗粒。本文提出利用大颗粒辐射强这一特点,使用高速相机对火箭发动机尾焰进行较长曝光时间的直接拍摄,获得相机曝光时间内大尺寸颗粒形成的粒子轨迹图像,采用粒子轨迹法[20-21]对尾焰中的大尺寸颗粒的速度进行测量。粒子轨迹法测速的关键是准确识别粒子轨迹长度,为此本文提出了一种一维拟合算法,以获得具有亚像素精度的粒子轨迹长度,并采用合成粒子轨迹图像来检验此算法的精度与计算效率。之后使用本文发展的图像处理程序采用粒子轨迹法对某固体火箭发动机尾焰中大尺寸颗粒的速度进行了全场测量,分析了尾焰中大尺寸颗粒速度特点。

1 测量原理及数据处理

1.1 粒子轨迹法速度测量原理

一般情况下,使用相机对发光颗粒摄像记录时,颗粒在相机成像平面上的像为圆斑。然而当颗粒高速运动时,即使曝光时间很短,颗粒的像在相机成像平面上的位移可能超过相机的最小成像单元(对于数字相机而言即一个像素,pixel)。此时粒子在相机中的像不是圆斑,而是圆斑在成像平面上不断移动形成的拖影,即粒子轨迹,如图1所示。

图1 粒子轨迹法测速原理Fig.1 Principle of particle streak velocimetry(PSV)

设相机成像的空间分辨率为Rs(m/pixel)、曝光时间为Δt(s),粒子轨迹法即为利用数字图像处理技术识别出图像中的独立的粒子轨迹并计算出其长度lp(pixel),因为曝光时间很短,可以假设曝光时间内粒子速度不变,则粒子轨迹为直线,所以粒子速度vp(m/s)可以表示为

(1)

因此,粒子轨迹法特别适合于测量高速运动的粒子速度。对于粒子轨迹法而言,相机的曝光时间可以从相机参数中准确读取,分辨率由成像系统决定,可以在测量之前标定,因此提高粒子轨迹法速度测量精度的关键是提高粒子轨迹长度lp计算精度。

1.2 亚像素精度粒子轨迹长度算法及精度检验

1.2.1 亚像素精度粒子轨迹长度算法

在得到含有粒子轨迹的图像后,首先需要判别出粒子轨迹。对于数字图像而言,这意味着判别出哪些像素属于某个特定的粒子轨迹,即所谓的图像分块(segmentation)。通常实验所得的图像为单色图像,因此判别的依据是粒子轨迹的亮度要高于背景流场,可用的算法包括亮度阈值以及边缘梯度等经过检验的分块算法。之后,需要根据分块得到的粒子轨迹图像来确定粒子轨迹长度。仅根据图像所包含的像素数目,只能得到像素级精度轨迹长度。为进一步实现亚像素级精度,需要借助相关模型,对粒子图像进行拟合。对大多数实际情况而言,粒子的图像主要来自于粒子所发光(或散射光)经成像系统衍射后的光斑[22],此类粒子图像的光强分布近似为高斯分布[23-24],则粒子轨迹的光强分布gs(x′)为[23-24]

(2)

其中,α为灰度值系数;x′为以轨迹灰度权重中心为原点的粒子轨迹坐标;n为沿粒子运动方向的单位矢量;σ为粒子散射光强分布参数;I0为与图像背景亮度有关的常数;G(x)为高斯函数:

(3)

根据式(2)对粒子轨迹图像的光强值进行拟合,可以得到亚像素精度粒子轨迹长度。本文中称此方法(或与之类似的方法,如采用不同的光强分布函数)为二维拟合(2D fit)算法。

二维拟合方法需要一次同时对α、lp、σ、I0及n共6个参数(n含有2个未知量)进行拟合,尤其是方向n的确定与其他参数耦合,通常需要多次迭代求解,计算速度较低。为此,提出了一种新的,同样具有亚像素精度,但计算较为简便的粒子轨迹长度算法。新算法的计算步骤如下:

(1)图像分块,得到单个粒子轨迹(详见1.2节中介绍的粒子轨迹识别程序)。

(2)得到每个粒子轨迹所在的直线方程。如果记粒子轨迹的直线方程为

y=kx+b

(4)

则此步目的是得到参数k与b,该参数组合通过对每个粒子轨迹采用带亮度值权重的最小二乘法进行直线拟合得到。为此,定义拟合误差函数Eerror为

(5)

式中wi为该粒子轨迹图像中像素亮度值。

根据最小二乘法可以求得式(4)中的k与b的值分别为

b=Sy-kSx

(6)

其中,

(7)

式(7)中的求和是针对这个粒子轨迹图像所含的所有像素。

(3)由于尾焰中粒子速度相对于轴线方向偏离很小,图像上粒子轨迹基本都为水平方向,因此可以沿竖直方向对轨迹图像降维,即计算粒子轨迹每列像素的亮度值之和I1D(x),其中x为列位置,如图2所示。

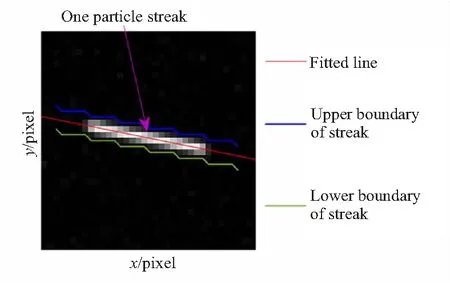
图2 亚像素精度轨迹长度一维拟合算法示意图Fig.2 Schematic diagram of sub-pixel accuracy particle streak length of 1D fitting algorithm

(4)对一维亮度函数I1D(x)进行拟合,得到粒子轨迹长度。将式(2)给出的粒子轨迹图像模型沿竖直方向积分可得一维亮度函数的模型函数:

(8)

其中,c1D、a1D、I0为常数;x0为粒子轨迹起点在x轴上的坐标;lp_x为粒子轨迹在x轴方向上的投影长度;erf(x)为误差函数,定义为

(9)

利用式(8)对I1D(x)进行拟合可得x0及lp_x。

(5)根据式(4),确定粒子轨迹长度lp为

(10)

如果需要,可以更近一步确定粒子轨迹的起点坐标(x0,kx0+b)以及终点坐标(x0+lp_x,k(x0+lp_x)+b)。将该方法被称为一维拟合(1D fit)算法。相比于原二维拟合算法,此方法需拟合5个参数c1D、a1D、x0、lp_x及I0,虽然看起来仅减少了1个拟合参数,但是剩余5个参数间耦合程度低,拟合收敛快。为更进一步节省计算时间,对I1D(x)拟合时可以将式(8)中的误差函数erf(x)用指数函数来近似,即用式(11)来代替式(8)。

(11)

将I1D(x)进行归一化后,使用式(8)与式(11)对某个颗粒轨迹的I1D进行拟合,结果如图3所示。从图3中可以发现式(8)与式(11)都可以很好地对I1D进行拟合。但采用式(11)进行拟合的优点是拟合算法更为简洁,无需计算误差函数erf(x),进一步减少计算量。

图3 两种形式拟合结果Fig.3 Fitting results of two equations

1.2.2 含有模拟粒子轨迹的合成图像的生成

为分析上述两种粒子轨迹长度算法(二维及一维拟合算法)的精度及计算效率,生成了各个参数已知的模拟粒子轨迹的计算合成图像(synthetic image),利用合成图像来检验上述算法。为生成模拟粒子轨迹图像,考虑一个自身发光或散射光的粒子在相机成像面对应的光强分布函数P(x,y)为

P(x,y)=f(x-xc,y-yc)

(12)

式中 (xc,yc)为粒子中心在相机成像平面的坐标。

理想情况下,球形颗粒在成像平面的光强分布函数P(x,y)为艾瑞斑(Airy disk),即

(13)

其中,A为系数;J1(r)为第一类贝塞尔函数;r为成像面上任意一点到粒子中心的距离:

(14)

对于实际成像系统,粒子散射光经过光学系统中一系列光学器件后其在像平面的光强分布近似为二维高斯函数[25],即

(15)

通常可以假设σx=σy=σ。

假设在相机曝光时间Δt内粒子以速度vxi+vyj(i与j是单位方向矢量)做匀速直线运动,则将光强分布对相机曝光时间Δt及像素区域积分后得到图像上任意像素(x1,y1)处的灰度值I(x1,y1)为

(16)

式中β为与成像系统有关的能量-灰度值转换系数。

在实际测量过程中,采集到的图像不可避免地会含有由于背景杂光引起的图像噪音。为此在生成的粒子轨迹模拟图像上添加了强度为γnoise的高斯白噪音,即图像上每一像素的实际亮度值为

(17)

式中 floor为取整函数;γnoise为代表噪音强度的参数;N(0,1)为服从均值为0,方差为1的高斯分布的随机变量;H代表图像位深,H=12。

计算生成的合成图像大小为1280 pixel × 384 pixel,每幅图像中有20个模拟粒子轨迹,轨迹的初始位置在图像中随机分布。为检验粒子轨迹拟合算法在不同工况下的精度,改变了模拟粒子轨迹的参数,包括:轨迹宽度σ、粒子轨迹长度lp、噪音强度γnoise,以及粒子轨迹方向Γ=vy/vx。各参数取值见表1。

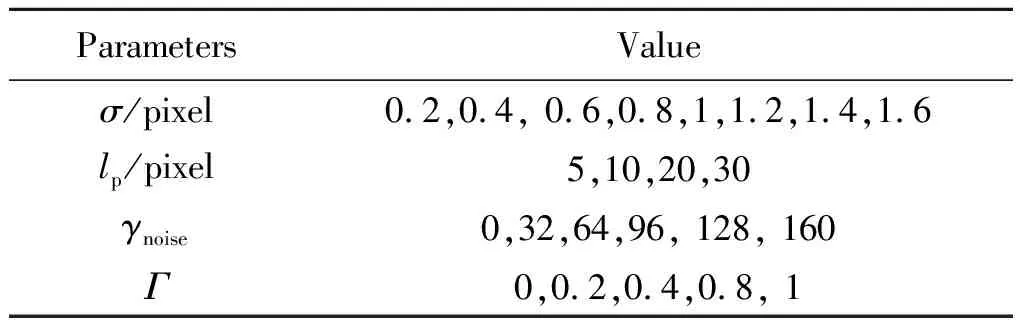
表1 模拟粒子轨迹图像参数Table 1 Parameters of the generated particle streaks

对应于表1中每种参数组合,生成了4000幅图像,即每种模拟工况下有80 000条模拟粒子轨迹。同时,为检验光强分布函数的影响,在每种模拟工况下,分别生成了光强分布为艾瑞斑与高斯分布的粒子轨迹。为保证可比性,假设在给定工况下无论粒子图像光强为何种分布,其所含辐射能量相同。由此易得在对应工况下高斯分布的参数σ与艾瑞斑参数A之间满足以下关系:

Aσ≈2

(18)

1.2.3 亚像素精度粒子轨迹长度算法精度

将拟合得到的粒子轨迹长度与合成图像时输入的模拟参数进行比较,可以得到拟合算法的粒子轨迹长度计算误差。结果表明,任意给定工况下,二维与一维拟合算法得到的粒子轨迹误差均值都为零。为定量评价误差的散布并避免极少数离群值的影响,定义粒子轨迹长度误差散布Δlp为[24, 26]

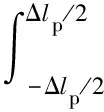
(19)

式中φ(x)为粒子轨迹长度误差的概率密度分布;Δlp为拟合得到的粒子轨迹长度80%的概率在真值附近[-Δlp/2,Δlp/2]的区间内。

不同工况下统计得到的误差散布Δlp如图4所示。

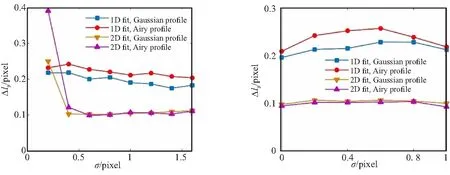
(a)γnoise=64,Γ=0.2,lp=20 pixel (b)γnoise=64,σ=0.6 pixel,lp=20 pixel

(c)γnoise=64,σ=0.6 pixel,Γ=0.2 (d)σ=0.6 pixel,Γ=0.2,lp=20 pixel图4 不同工况下算法精度Fig.4 Algorithm accuracy for different conditions

从图4(a)可以发现,对于大多数测试的粒子轨迹宽度,二维拟合算法精度要高于一维拟合精度,这是符合预期的。然而,对于一维拟合算法,随着图像宽度增加拟合精度略有提高,对于二维拟合算法,随着粒子轨迹宽度增加拟合精度略有降低。

尤为特别的是,当粒子轨迹宽度σ<0.4 pixel时,不论是粒子图像光强分布是高斯分布还是艾瑞斑分布,一维拟合算法精度都比二维拟合的精度高。这是因为当σ<0.4 pixel时(算例中σ=0.2 pixel)散射能量在垂直于粒子运动方向上集中在一个窄于一个像素的宽度内,由于图像是以像素为单位离散化的,因此会出现沿粒子运动方向,同一个粒子轨迹在不同位置的光强分布在一个或两个像素的情况,而相关像素的亮度值会剧烈变化,这导致二维拟合算法精度降低。对于一维拟合算法,由于将粒子轨迹所涉及像素的亮度在水平方向(接近粒子运动方向)加和,相当于将粒子图像所含的能量在垂直于运动方向进行了积分,这消除了粒子图像在垂直于运动方向分布于几个像素的影响,所以一维拟合精度几乎不受影响,故当粒子轨迹宽度较小时,一维拟合算法的精度高于二维拟合算法精度。

此外,粒子图像的光强分布形式对一维拟合算法精度有一定影响:在相同粒子轨迹宽度下,一维拟合算法对粒子光强分布为高斯分布的轨迹长度计算精度略高于光强分布为艾瑞斑时的计算精度。这应该是由于拟合所用的算法,即式(8)或其近似式(11),是基于高斯光强分布导出的。二维拟合算法的精度则对粒子图像的光强分布不敏感,对于高斯分布和艾瑞斑分布得到的结果几乎一样。这是由于虽然二维拟合时也采用了粒子光强分布为高斯分布的假设,但是二维拟合时更多利用到图像的空间分布信息。从图4(b)～(d)可以发现,这一规律对其他参数变化时也同样成立,因此后文中不再赘述。值得指出的是,对于实际的光学成像系统,粒子图像的光强分布更接近于高斯分布,因此采用式(8)或式(11)进行拟合是合理的。

图4(b)表明,粒子运动方向无论对一维拟合算法还是二维拟合算法的精度都只有非常微弱的影响。

粒子轨迹长度对算法精度的影响体现在图4(c)中:一维和二维拟合算法的精度都先随着粒子轨迹长度的增加而增加,但当粒子轨迹长度大于大约20 pixel 后,轨迹长度进一步增加对计算精度就不再有影响,无论是采用一维还是二维拟合都是如此。这个结果对于实际实验测量具有重要的指导意义,可用于调整相机曝光时间以获得最佳的粒子轨迹长度。因为如果曝光时间过长形成过长的粒子轨迹的话,出现粒子轨迹交叉的可能性也增加,这会给图像处理带来额外的困难。实际上,图4(c)的结果表明,如果实际测量时粒子过浓,为避免粒子轨迹交叉,可以考虑通过缩短曝光时间将粒子轨迹长度降至10 pixel左右,这只带来轨迹长度测量精度的略微降低。

图4(d)给出了图像噪音水平对轨迹长度测量精度的影响:两种算法的误差散布都随着图像噪音水平增大而几乎线性增大。注意图中横轴的噪音强度为背景高斯噪音的标准差(standard deviation),对于生成的12-bit合成图像,噪音强度为128(即7-bit)已是非常强烈的背景噪声了。即便是这种情况下,两种拟合算法的精度依然是亚像素级。实际情况下,通过对原始图像进行去噪滤波,可以进一步降低背景噪音的影响。

通过以上分析发现,通常情况下,二维拟合算法的精度都略优于一维拟合算法,但只要粒子轨迹长度不过短,如不低于20 pixel,一维拟合算法计算得到单个粒子轨迹长度的相对误差即使在背景噪音很强烈的情况下也不超过±2%。尤其值得指出的是,这是指单个粒子轨迹长度的测量误差,对于统计量,如粒子的平均速度,因为算法的无偏性,其误差更小。

除了分析不同工况下两种算法的精度,还比较了两种方法计算轨迹长度所用时间,统计而言,对同一条粒子轨迹,二维拟合算法所用时间约是一维拟合算法的8倍。综合考虑算法精度和算法计算效率,在后续实验测量中采用一维拟合算法进行粒子轨迹长度计算。

1.3 固体火箭发动机尾焰中颗粒速度测量

利用前文介绍的粒子轨迹法,对一真实固体火箭发动机尾焰中颗粒的速度进行了实验测量。在本小节中,对实验装置布置和所用计算程序进行简要介绍。具体实验结果及讨论则在第2节中详细叙述。

1.3.1 实验装置

固体火箭发动机尾焰中较大的颗粒其亮度通常比背景亮度高,因此,实验时采用对尾焰直接摄影的方法,无需设置额外的照明光源,如图5所示。

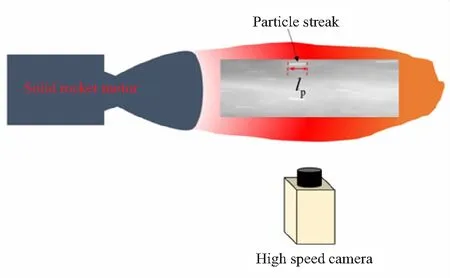
图5 固体火箭发动机尾焰中颗粒速度测量原理示意图Fig.5 Schematic diagram of particle velocity measurement in solid rocket motor

实验时,采用高速相机正对地面热试车中的固体火箭发动机尾焰区拍摄。本文中使用的高速相机型号为Phantom 710L单色相机,镜头焦距105 mm,图像幅面设置为1280 pixel×384 pixel。在实验开始前先标定得到的成像系统空间分辨率Rs=0.37 mm/pixel,标定时采用高速相机拍摄表面加工有规则圆斑阵列的标定板,对拍摄得到的图像处理后得到标定图像中两圆斑的图像间距(单位为像素),则圆斑间物理间距除以对应图像间距即为空间分辨率Rs,经估算标定误差不超过1%。高速相机距离发动机尾焰大约1.5 m。通过对尾焰中粒子速度的预估,结合标定得到的成像系统空间分辨率,设置高速相机曝光时间Δt为9.41 μs,使得图像上粒子轨迹长度大约为25 pixel。相机拍摄帧速为15 000 fps,接近该幅面下相机所能支持的最高拍摄速度。高速相机的拍摄开始时刻由外部触发信号控制,该外部触发信号可以是火箭发动机的点火信号或者由实验者设置的其他信号。

1.3.2 发动机尾焰图像中粒子轨迹识别

利用高速相机拍摄得到发动机尾焰图像后,需要识别出尾焰图像中的粒子轨迹。由于尾焰中存在细小的颗粒云团,这使得尾焰图像背景噪音较大,粒子轨迹识别程序需要从背景噪音中分辨出单个的粒子轨迹。性能良好的粒子轨迹识别程序是进行尾焰中颗粒速度测量的重要步骤。本文用MATLAB语言编写了对数字图像的粒子轨迹识别程序,其主要流程如图6所示。

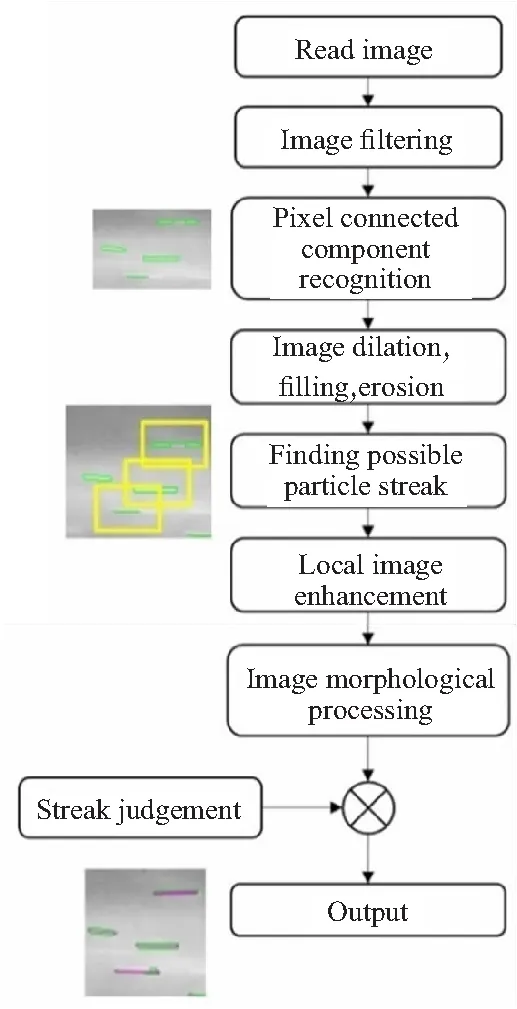
图6 图像中粒子轨迹识别主要过程Fig.6 Main process of particle streak recognition in image

在读入图像后首先对图像去噪,本文中使用均值滤波去噪音。图像去噪后利用图像灰度值梯度阈值进行粒子轨迹边缘识别得到二值图(binary image),找到二值图中的8邻域连通区,并去掉小的连通区,因为这些小的区域对应的是图像中残余噪声。之后对通过筛选的二值图像进行图像膨胀(dilation),图像膨胀用的卷积核为3×3。图像膨胀的目的是进行图像填充,以补充轨迹中间灰度梯度较小而未能被梯度阈值法识别部分,但图像膨胀也使得粒子轨迹图像向四周扩展,因此再用3×3的卷积核对图像进行腐蚀(erosion),以恢复粒子轨迹的大小[27]。

经过上述操作后可找到疑似粒子轨迹,之后以疑似粒子轨迹为中心,划分较小的粒子轨迹检测区,进行第二次粒子轨迹识别。对这些小的粒子轨迹检测区利用局部直方图法进行局部图像增强[28],对增强后的检测区再进行图像膨胀、腐蚀、边缘检测等一系列处理,其中边缘检测使用Sobel算法。局部图像增强一方面可以避免将一个颗粒轨迹误识别为多个轨迹,另一方面可以提高颗粒轨迹起始点位置识别精度。此处得到的轨迹起始点位置作为亚像素精度轨迹长度算法拟合的初值,较高精度的拟合初值可以减少拟合计算所用时间。

上述处理后,图像中的单个噪点不会影响轨迹识别结果,但亮度变化剧烈的区域,如较亮的颗粒云团边缘仍可能被错误识别为粒子轨迹。为此引入粒子轨迹的判别条件以去除误识别的轨迹。粒子轨迹判别条件包括:(1)颗粒的轨迹应该是直线状;(2)单幅图像上粒子轨迹长度(即在给定的曝光时间内颗粒飞行的距离)不可能超过某一上限(该上限可以通过对颗粒速度最大值的估计来确定);(3)颗粒速度矢量指向不应违反物理规律,如速度矢量应该远离中心线,而非指向中心线。利用此判别准则得到最终粒子轨迹,记录粒子轨迹长度、端点位置、出现时刻等,用于后续颗粒速度统计分析。

经过以上图像处理过程,得到了图像中代表单个粒子轨迹图像的一组连续的像素,对此应用前文介绍的一维拟合算法得到具有亚像素精度的粒子轨迹长度。

2 结果与讨论

在前文介绍的对某固体火箭发动机测试过程的现场测量中,共得到25 910幅图像。对其利用本文所介绍的粒子识别程序对图像中的粒子轨迹进行识别,共识别出粒子轨迹约400 000个。图7(a)所示为某时刻的该固体火箭发动机尾焰图像及识别出的尾焰中粒子轨迹,图中黄色框表示本文中粒子识别程序处理的图像范围,紫色箭头从程序识别出的粒子轨迹起点指向粒子轨迹终点,图7(b)为粒子轨迹局部放大图,图中粒子轨迹宽度约为3 pixel,其他粒子轨迹图像多与之相似。考虑粒子成像系统的放大比、光圈大小以及衍射效应,根据文献[29]可以估计粒子直径约为100～200 μm。

识别单个粒子轨迹,并利用前文介绍的一维拟合算法对粒子轨迹长度进行计算,根据式(1)得到粒子瞬时速度。图8中给出了在拍摄时间段内,距离喷管82、228、430 mm处粒子轴向平均速度随时间的变化。该平均速度为在相应位置处每300帧图像(对应的时间为 0.02 s)中所有粒子速度的平均值。如前所述,利用粒子轨迹法计算颗粒速度时,对于颗粒轨迹长度平均值,粒子轨迹长度算法是无偏的。实验结果表明,在拍摄时间段内三个不同位置处的颗粒平均速度随时间没有明显变化。因此接下来对得到的粒子速度在整个拍摄时间段内平均,以计算尾焰流场内不同位置处颗粒的平均速度。

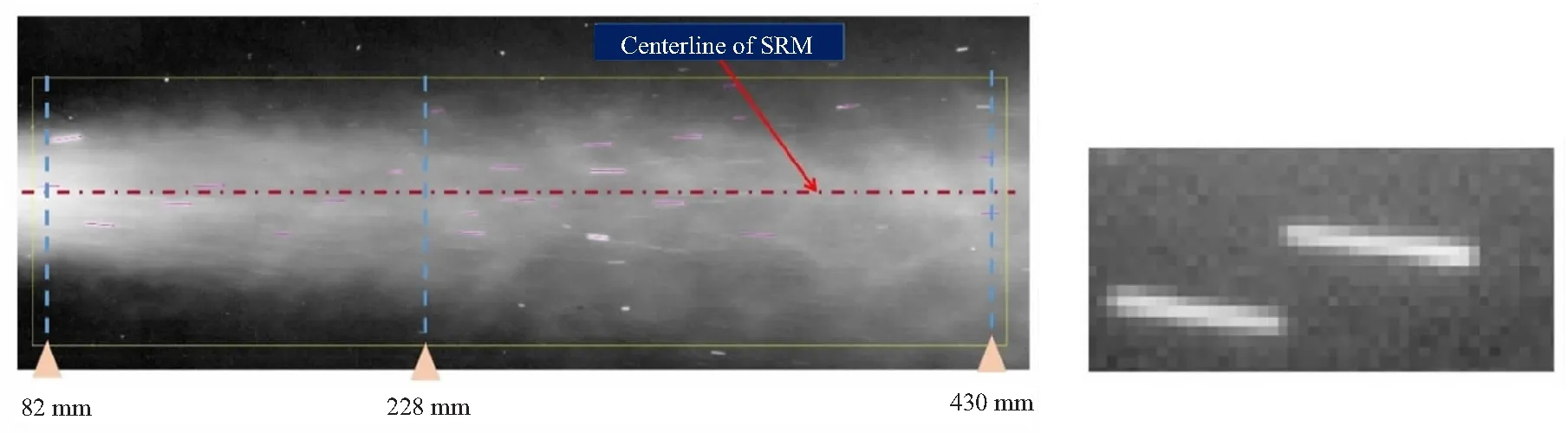
(a)Recognition results of particle streaks in SRM plume for one image (b)Enlarged view of particle streaks图7 尾焰流场及粒子轨迹局部放大图Fig.7 Image of plume field and enlarged view of particle streaks

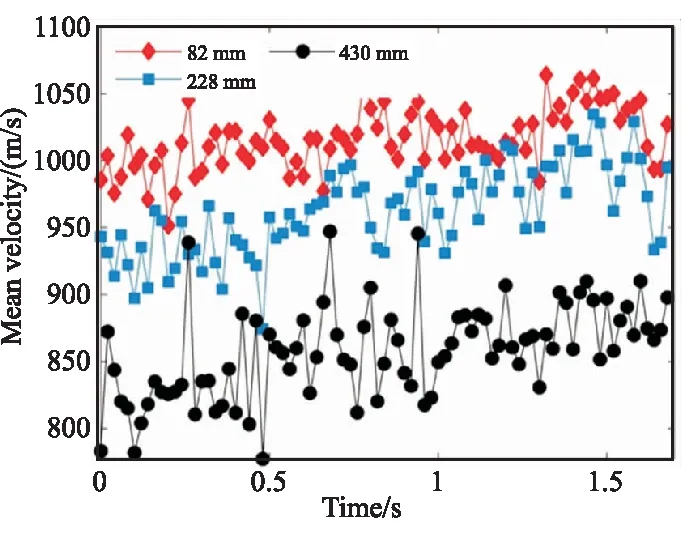
图8 尾焰中3个不同位置处颗粒平均速度随时间变化关系Fig.8 Mean particles velocityin three different locations varies with time

图9所示为尾焰不同位置处颗粒轴向平均速度。从图9可以看出尾焰中的粒子速度在靠近喷管出口处最大,超过1000 m/s,随着距喷口距离的增加尾焰中的粒子速度降低,但粒子速度随着距离衰减特性与气相湍流射流的速度衰减特性不同:大尺寸粒子速度衰减弱于气相湍流射流的速度衰减,这是因为大粒子的斯托克数较大造成的。

图9 平均颗粒轴向速度随距离喷口位置的变化Fig.9 Mean particles axial velocity varies with distance from the nozzle

被测发动机尾焰为超音速气流,根据发动机设计参数仿真计算表明尾焰中存在马赫盘。为观察是否有大尺寸颗粒穿过激波后发生速度突变,图10中给出了二维流动平面内粒子速度幅值分布的等值线图(图中左下角处白色区域是因为在该处没有拍摄到粒子轨迹,故该处没有粒子速度数据)。

图10 全流场中颗粒平均速度分布Fig.10 Mean particles velocity distribution in full plume field

与前面轴向平均速度类似,从图10中可以发现:靠近喷管轴线位置处粒子速度最高,随着远离轴线,粒子速度降低。因为稳态射流流场中激波位置是固定的,如果粒子速度受到流场中激波明显影响的话,从该图中应该可以观察到在空间中某些位置出现粒子速度剧烈变化的区域。然而图中并不存在类似区域,表明尾焰中激波对于观察到的大尺寸粒子的速度没有显著影响。

3 结论

本文采用合成图像对粒子轨迹测速法中的粒子轨迹长度拟合算法进行了仿真分析,并开发了完整的粒子轨迹测速法程序,对某固体火箭发动机尾焰中大尺寸颗粒速度进行了实验研究,得到以下结论:

(1)模拟颗粒轨迹计算结果表明,本文提出的一维拟合粒子轨迹亚像素精度长度算法计算效率高,单个粒子轨迹长度计算的不确定性都在亚像素精度。为减小单个粒子轨迹长度的相对误差,最有效的方法是使得实验图像中粒子轨迹的长度约为20 pixel,至少不短于10 pixel。此外,拟合算法得到的粒子轨迹长度平均值是无偏的。

(2)该发动机尾焰流场中颗粒速度测量误差约为3%。粒子轨迹法可以实现尾焰流场中大尺寸颗粒速度测量,该技术为尾焰中大尺寸颗粒的速度测量提供了新的思路。

(3)测量结果表明,固体火箭发动机尾焰中的大尺寸颗粒速度随着距喷管中心距离增加而减小,也随距喷管出口的轴向距离增加而衰减,但是衰减速度小于气相湍流射流中的速度衰减。结果中未观察到尾焰中激波对大尺寸颗粒速度产生影响。

致谢：感谢基础科研项(JCKY2019204B020)的支持。