基于梯度有限元法的HTPB推进剂药柱结构完整性分析①
周东谟,王 辉,惠步青,吴晗旭,陈 航
(1.中北大学 机电工程学院,太原 030051;2.内蒙古动力机械研究所,呼和浩特 010010; 3.中国人民解放军 陆军步兵学院石家庄校区,石家庄 050020)
0 引言
推进剂药柱作为固体火箭发动机的主要结构件和承力件,其结构完整性是决定发动机可靠工作与贮存寿命的关键因素[1-2]。固体火箭发动机药柱在全寿命周期内要承受温度、振动、冲击、飞行加速度和点火增压等载荷的作用[3-5]。载荷的长期作用使药柱内部结构发生复杂的物理化学变化,影响其力学性能与本构特性,最终导致药柱力学性能的空间分布不均匀,即同一药柱的不同部位其力学性能存在差异。传统的基于推进剂力学性能均匀性假设的药柱结构完整性评估方法不能准确反映这一差异,因此开展考虑推进剂力学性能非均匀性的药柱结构完整性评估具有重要意义[6-8]。
考虑药柱力学性能的空间分布不均匀性时,推进剂材料力学性能参数为空间坐标的函数,其参数求解的基本方程通常是变系数的,数学上很难求出解析解[9-11]。近年来,研究者发展了多种解决材料力学性能非均匀性的数值方法,如细观元法[12-13]、扩展多尺度有限元法[14-17]、光滑有限元法[18-19]、分层单元有限元法[20-21]、等参梯度有限元法[22-25],这为力学性能非均匀的材料构件分析提供了有效途径。当材料的力学性能在空间上呈梯度变化时,采用这些数值方法大多需要构造与坐标相关的单元本构矩阵,对于构型复杂的结构零部件,存在单元本构矩阵构造繁琐,有限元计算工作量大的问题。
贴壁浇注式药柱在固化降温结束后,长期处于非均匀定应变作用状态,定应变的拉伸作用会使HTPB粘合剂高分子链取向并重新排列且在受力方向上取向增多,在一定程度上会提高推进剂的延伸率[26]。同时,定应变也可能造成HTPB推进剂基体与颗粒界面的损伤从而降低其延伸率[27]。这主要与推进剂的具体组分及定应变载荷大小相关。本文以此为背景,构建HTPB推进剂药柱力学性能非均匀特征,采用一种简便快捷的梯度有限元法开展推进剂药柱结构完整性评估,研究推进剂力学性能非均匀性对药柱结构完整性的影响,研究结果有助于进一步提升发动机药柱结构完整性评估的准确性,同时研究方法可推广到其他复合固体推进剂药柱结构完整性评估中。
1 基于梯度有限元法的药柱结构完整性评估方法
基于梯度有限元法的推进剂药柱结构完整性评估方法,其本质是通过指定材料属性变化函数的药柱结构完整性有限元分析方法。该方法能充分考虑推进剂材料性能空间分布不均匀性对药柱结构完整性的影响,且在保证计算精度的前提下,单元数量、自由度数及计算工作量均较低,保留了传统有限元法对求解问题普遍适应性与程序统一性的特点,对复杂几何构形和各种物理问题具有很强的适应性。
基于梯度有限元法的推进剂药柱结构完整性评估方法实现流程为:首先,采用零载荷下推进剂本构模型及物性参数对药柱承受的初始载荷进行分析,确定其初始载荷场,获取求解单元各节点的载荷数据;其次,结合构建的考虑载荷影响的推进剂本构模型及物性参数模型,赋予各节点材料本构参数及物性参数,建立推进剂药柱力学性能的空间分布场;最后,基于有限元法开展推进剂药柱在工作载荷下的力学响应分析,并结合推进剂失效判据,开展其结构完整性评估。具体流程如图1所示。

图1 药柱结构完整性评估流程Fig.1 Evaluation process of grain structural integrity
2 本构模型
2.1 应力-应变曲线
研究显示,在定应变载荷作用下,HTPB推进剂单轴拉伸本构特性存在两种典型特征。
Ⅰ型:在线弹性段,不同定应变作用下HTPB推进剂应力-应变曲线基本重合;在应力平台段,不同定应变作用下HTPB推进剂应力-应变曲线基本平行,即定应变对HTPB推进剂的模量基本没有影响,但定应变会引起界面的微损伤,降低推进剂的损伤应变阈值[33]。图2(a)为55 ℃、3%、6%和9%定应变下贮存296 d后的HTPB推进剂应力-应变曲线,具体参见文献[26]。
Ⅱ型:在线弹性段与应力平台段,不同定应变作用下HTPB推进剂应力-应变曲线均无重合,定应变越大,对推进剂的损伤越严重,在一定范围内会导致推进剂模量的降低,并且降低其最大延伸率和损伤应变阈值[27],据此,本文基于文献[27]的试验研究结果构建不同定应变作用下推进剂材料的应力-应变曲线,如图2(b)所示。

(a)Type I HTPB propellant
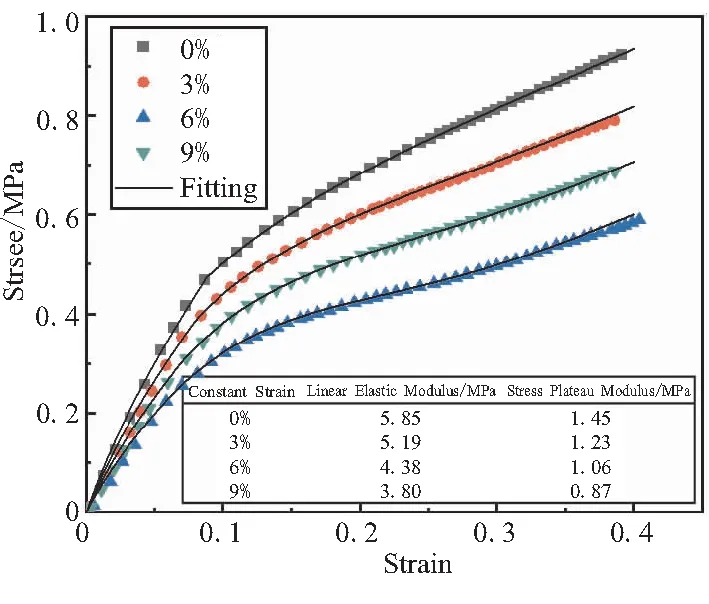
(b)Type II HTPB propellant图2 HTPB推进剂应力-应变曲线Fig.2 Stress-strain curves of HTPB propellants
2.2 本构模型及参数标定
本文采用含损伤的非线性ZWT本构模型,其本构关系为
(1)
fe(ε)=σm[1-exp(-αε)]
(2)

对图2中两型推进剂应力-应变曲线进行拟合分析,分别以3%、6%和9%定应变下的推进剂单轴拉伸曲线为基础,对式(1)~式(3)中的本构模型参数拟合分析,获得含定应变的本构模型参数如表1所示。根据文献[26]-[27]的研究结果,图2中两型推进剂最大延伸率εm随定应变变化关系如表2所示。

表1 推进剂本构模型参数Table 1 Parameters of propellant constitutive model

表2 推进剂最大延伸率随定应变变化关系Table 2 Variation of maximum elongation ofpropellant with constant strain
2.3 有限元实现
在进行三维有限元计算时,ZWT非线性本构模型一维形式不能直接带入ABAQUS软件中进行计算,需将一维本构模型离散至三维形式,获得本构模型在有限元软件中应力更新方程及雅可比矩阵。在外力作用下,通常将一点的应力-应变分解为偏张量和球张量两部分[28-30]。
σij=Sij+δ0σ0
(4)
εij=eij+δ0ε0
(5)
式中δ0为克罗内克符号;Sij和eij分别为应力偏张量和应变偏张量;σ0和ε0分别为应力球张量和应变球张量。
由于应变球张量为体积应变的1/3,故应力偏张量和应力球张量可以表示为
Sij=2Geij
(6)
(7)
式中εv为体积应变;G=E/2(1+ν)为剪切模量;K=E/3(1-2ν)为体积模量;ν为泊松比。
不考虑推进剂材料损伤时,将式(1)中的本构模型分为非线性和粘弹性两部分,将推进剂材料视为各向同性的,基于唯象法可获得非线性部分的弹性模量:
(8)
其中,σeq为等效应力,εeq为等效应变,将其带入非线性部分整理后可得非线性部分的三维形式:
(9)
根据非线性ZWT本构模型各部分的物理意义,同理可得粘弹性项的三维形式:
(10)
将损伤变量视为各向同性,即损伤变量是关于等效应变的函数[31-32],在三维应力状态下,损伤变量可以表示为
(11)
综合式(9)~式(11),可得含损伤的非线性粘弹性本构模型的三维形式:
(12)
在获得本构模型的三维形式后,根据其增量关系获得本构模型的各部分的应力增量以及雅可比矩阵,实现有限元计算所需要的应力更新。由式(9)可知,非线性部分的应力增量关系可以表示为
(13)
式中λ为拉梅常数,λ=ν/[(1+ν)(1-2ν)]。
推导粘弹性部分应力增量关系时,将粘弹性部分又分为剪切应力和体积应力部分两部分进行推导。因此,在 时刻粘弹性部分的剪切应力增量关系为
(14)
令其中:
(15)

(16)
同理可得体积应力增量:
(17)

结合式(16)、式(17)可获得粘弹性部分的应力增量:
(18)
综合式(13)、式(18)可得不考虑损伤时的非线性ZWT本构模型增量形式:
(19)
将损伤变量对时间的导数定义为动态损伤演化率,且当Δt很小时,将dD近似为ΔD,损伤变量的增量关系可以表示为
(20)
结合式(19)、式(20)得含损伤的ZWT非线性本构模型的增量形式:
(21)
雅可比矩阵通常表示为应力增量对应变增量的偏导,当考虑推进剂材料损伤时,将损伤变量视为标量形式,故可以得到考虑损伤的雅可比矩阵:
(22)
其中,
(23)
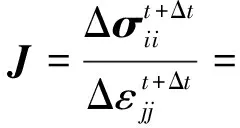
(24)
(25)
2.4 数值模拟验证
基于2.3节推导的本构模型三维扩展形式,利用ABAQUS软件的二次开发功能,编制UMAT子程序,数值模拟定应变作用后推进剂方坯试样的单轴拉伸试验,以验证上述推导方法和UMAT子程序编写的正确性。选取图2中3%定应变试验数据作为验证对象,取单轴拉伸试样中间截面中心点作为参考点,获得试样在拉伸过程的应力-应变仿真曲线,与试验应力-应变曲线进行对比,结果如图3所示。由图3可见,数值仿真结果和试验结果吻合较好,这表明二次开发的UMAT子程序能有效模拟推进剂应力-应变响应。

图3 定应变下的单轴拉伸试验结果与仿真结果对比Fig.3 Comparison between simulation results and uniaxialtensile test results under constant strain
3 药柱结构完整性评估
3.1 有限元建模
本文中采用3段式翼柱型贴壁浇注式固体发动机,由壳体、绝热层、药柱三部分构成,在发动机前端紧挨药柱与壳体部分的绝热层中设置人工脱粘层。取1/20实体发动机进行三维建模,采用结构化六面体网格,壳体单元类型为C3D8,由于绝热层和药柱的泊松比高于0.495,故采用防止沙漏效应的C3D8H杂交单元,单元共计24 768个单元,29 508个节点,如图4所示。

图4 发动机有限元网格模型Fig.4 Mesh division of solid rocket motor
3.1.1 材料参数
本文采用的两型推进剂均为HTPB/AP/Al三组元复合固体推进剂,配方略有不同。为准确识别推进剂力学性能的非均匀性对药柱结构完整性的影响,两型HTPB推进剂的密度、泊松比、线膨胀系数、热传导率,以及壳体、绝热层材料参数均取值一致,如表3所示。
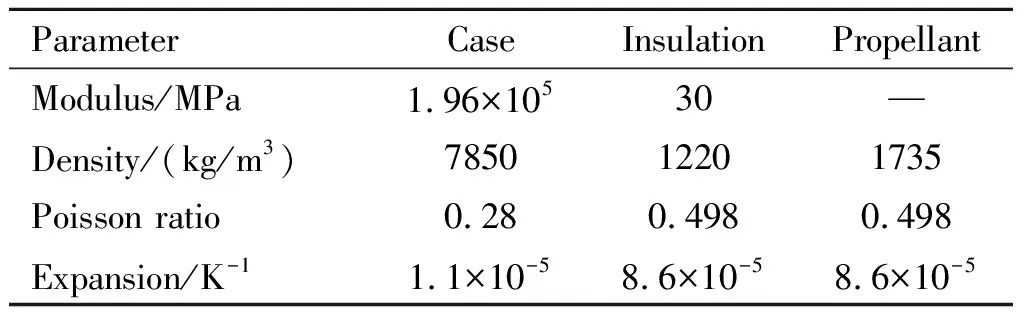
表3 发动机其他部件材料参数[33]Table 3 Material parameters of SRM parts[33]
3.1.2 边界条件及计算工况
有限元模型边界条件:
(1)壳体-绝热层-推进剂界面均采用Tie接触;
(2)壳体外表面采用固定约束,对称面设置对称边界条件。
计算工况:
(1)Step-1,固化降温。固体火箭发动机由固化温度50 ℃降至常温20 ℃,其中零应力温度为58 ℃。
(2)Step-2,点火增压。常温下点火过程中假定药柱内孔压力在0.345 s内由0 MPa增加到10 MPa,由于点火建压过程时间较短,点火压力可看成是线性增长过程。
3.2 固化降温载荷分析
两型推进剂材料采用零应变下各自的初始模量,基于ABAQUS有限元软件对其药柱在固化降温工况下的力学响应进行数值分析,结果如图5、图6所示。

(a)Equivalent stress contour of grain(MPa)

(b)Equivalent strain contour of grain图5 I型推进剂药柱固化降温后的力学响应Fig.5 Mechanical response of Type I propellantgrain under curing and cooling load

(a)Equivalent stress contour of grain(MPa)

(b)Equivalent strain contour of grain图6 Ⅱ型推进剂药柱固化降温后的力学响应Fig.6 Mechanical response of Type Ⅱ propellantgrain under curing and cooling load
由图5、图6可知,在固化降温载荷下,两型推进剂药柱的应力/应变呈现不均匀分布,在药柱内孔中部、人工脱粘层处、前后端翼槽处等关键部位的承载较大,Ⅰ型推进剂药柱的最大固化应力约为0.29 MPa,最大固化定应变约为0.072 4;Ⅱ型推进剂药柱的最大固化应力约为0.35 MPa,最大固化定应变约为0.072 3。
3.3 药柱力学性能空间分布
为进一步分析HTPB推进剂药柱力学性能的空间分布特性,在获得药柱固化定应变场后,读取药柱求解单元各节点的等效应变数据,利用FORTRAN语言编制推进剂力学性能参数与定应变关系的UMAT子程序,然后赋予药柱模型各节点材料力学性能参数,最终获得HTPB推进剂药柱力学性能参数的空间分布场,如图7~图10所示。
定应变对Ⅰ型推进剂的模量基本没有影响,因此药柱内部推进剂线弹性段及应力平台段的模量分布均匀,且与常规不考虑推进剂力学性能非均匀时相同,分别为5.51 MPa与1.67 MPa,如图7所示。但对于Ⅱ型推进剂,定应变能降低线弹性阶段和应力平台段的模量,由于固化定应变的差异,药柱内部推进剂线弹性阶段和应力平台段的模量呈空间分布状态,药柱中的推进剂线弹性阶段模量于4.17~5.84 MPa之间分布,应力平台段模量于0.98~1.44 MPa之间分布,相对常规不考虑推进剂力学性能非均匀时的5.85 MPa与1.45 MPa,药柱推进剂在线弹性阶段与应力平台段的最低模量分别降低了28.7%与32.4%,模量与固化定应变的分布呈负相关,如图8所示。
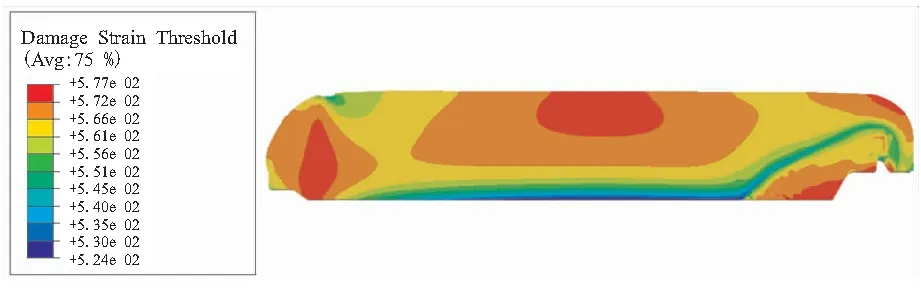
定应变能够降低Ⅰ、Ⅱ型推进剂药柱的损伤应变阈值,致使药柱内部损伤应变阈值呈现空间不均匀分布,Ⅰ型推进剂药柱的损伤应变阈值在0.052 4~0.057 7之间分布,最小损伤应变阈值相对于不考虑推进剂力学性能非均匀时的0.06降低了12.7%;Ⅱ型推进剂药柱的损伤应变阈值在0.065 8~0.088 1之间分布,最小损伤应变阈值相对于不考虑推进剂力学性能非均匀时的0.09降低了26.9%;两型推进剂药柱的损伤应变阈值均与固化定应变的分布呈负相关,如图9所示。
定应变能提升Ⅰ型推进剂的最大延伸率,致使Ⅰ型推进剂药柱最大延伸率在0.557~0.768之间内呈现不均匀分布,最大延伸率与固化定应变呈正相关,相对于不考虑推进剂力学性能非均匀时的0.56,药柱在关键部位的应变承载能力提升了37.1%;由于定应变能降低Ⅱ型推进剂的最大延伸率,致使Ⅱ型推进剂药柱最大延伸率在0.461~0.578之间内呈现不均匀分布,最大延伸率与固化定应变呈负相关,相对于不考虑推进剂力学性能非均匀时的0.58,药柱在关键部位的应变承载能力下降了20.5%,如图10所示。

(a)Modulus of linear elastic segment

(b)Modulus of stress platform segment图7 Ⅰ型推进剂药柱模量分布云图(MPa)Fig.7 Modulus distribution of Type I propellant grain
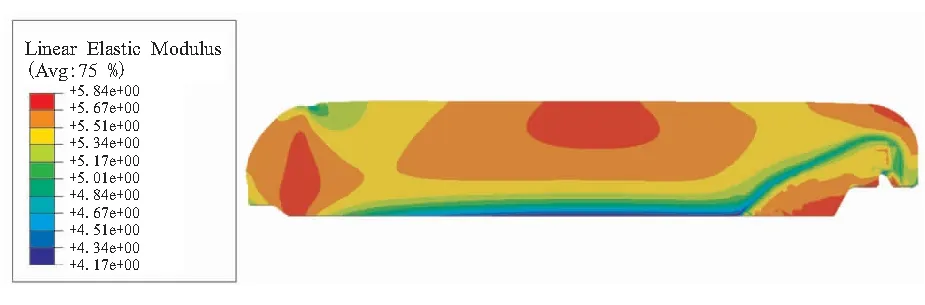
(a)Modulus of linear elastic segment

(b)Modulus of stress platform segment图8 Ⅱ型推进剂药柱模量分布云图(MPa)Fig.8 Modulus distribution of Type Ⅱ propellant grain
(a)Type I propellant grain

(b)Type II propellant grain图9 两型推进剂药柱损伤应变阈值分布云图Fig.9 Damage strain threshold distribution of grains

(a)Type I propellant grain

(b)Type II propellant grain图10 两型推进剂药柱最大延伸率分布云图Fig.10 Maximum elongation distribution of grains
由此可见,在考虑固化定应变对推进剂力学性能的影响时,固化定应变的作用会导致推进剂药柱模量、损伤应变阈值、最大延伸率等力学参数的空间不均匀分布,最终会引起药柱在外载荷作用下的力学响应及承载能力的改变。因此在开展推进剂药柱结构完整性评估时,应充分考虑推进剂药柱力学性能的不均匀性。
3.4 药柱结构完整性分析
3.4.1 药柱力学响应分析
在点火增压工况下,药柱力学响应如图11~图14所示。考虑推进剂力学性能非均匀与否时,Ⅰ型推进剂药柱和Ⅱ型推进剂药柱的最大等效应力和等效应变均出现在药柱内孔中部。考虑推进剂力学性能非均匀性影响时,Ⅰ型推进剂药柱最大等效应力相较于不考虑时由0.80 MPa下降到0.78 MPa,下降幅度约为2.5%;最大等效应变由0.233提高到0.239,提升幅度约为2.6%。虽然固化定应变对Ⅰ型推进剂的模量几乎没有影响,但其损伤应变阈值随固化定应变的增大而减小,因此考虑推进剂力学性能非均匀性时,在点火增压工况下推进剂提前进入损伤状态,等效降低其模量,导致药柱应力响应降低,应变响应提高。
考虑推进剂力学性能非均匀性影响时,Ⅱ型推进剂药柱最大等效应力相对于不考虑时由0.87 MPa下降到0.74 MPa,下降幅度约为14.9%;最大等效应变由0.263提高到0.299,提升幅度约为13.7%,显然,这是由于固化定应变降低Ⅱ型推进剂模量所致。为了进一步研究推进剂力学性能非均匀性对点火增压工况下药柱力学响应的影响,选取如图15所示的3条路径进行分析。

(a)Considering the heterogeneity of propellant mechanical properties

(b)No considering the heterogeneity of propellant mechanical properties图11 I型推进剂药柱等效应力云图(MPa)Fig.11 Equivalent stress contours of Type I propellant grain

(a)Considering the heterogeneity of propellant mechanical properties

(b)No considering the heterogeneity of propellant mechanical properties图12 I型推进剂药柱等效应变云图Fig.12 Equivalent strain contours of Type I propellant grain

(a)Considering the heterogeneity of propellant mechanical properties
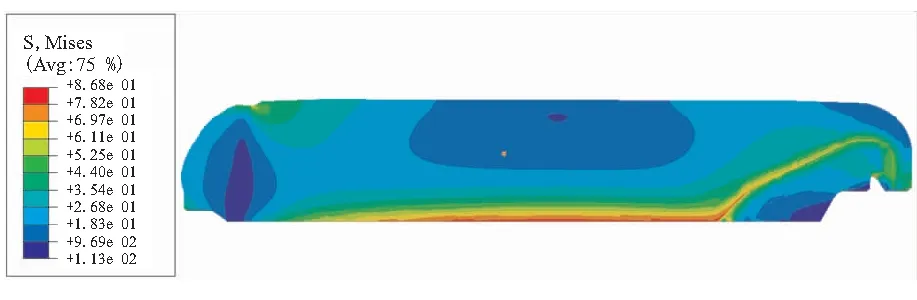
(b)No considering the heterogeneity of propellant mechanical properties图13 Ⅱ型推进剂药柱等效应力云图(MPa)Fig.13 Equivalent stress contours of Type Ⅱ propellant grain

(a)Considering the heterogeneity of propellant mechanical properties

(b)No considering the heterogeneity of propellant mechanical properties图14 Ⅱ型推进剂药柱等效应变云图Fig.14 Equivalent strain contours of Type Ⅱ propellant grain

图15 分析路径选择Fig.15 Analysis path selection
图16为药柱等效应力沿路径1~3的变化曲线。图17为药柱等效应变沿路径1~3的变化曲线。
由图16可知,两型推进剂药柱在考虑推进剂力学性能非均匀性与否时,在路径1上等效应力几乎没有差异;考虑推进剂力学性能非均匀性时,两型推进剂药柱应力响应的差异主要出现在圆柱段内孔中部。在考虑推进剂力学性能非均匀性影响时,Ⅰ型推进剂药柱内孔中部的最大等效应力相较于不考虑时下降幅度约为2.5%;Ⅱ型推进剂药柱的最大等效应力相较于不考虑时下降幅度约为14.9%。
由图17可知,两型推进剂药柱在考虑推进剂力学性能非均匀性与否时,在路径1上等效应变计算结果几乎没有差异,但在药柱内孔中部,考虑推进剂力学性能非均匀性影响时,Ⅰ型推进剂药柱最大等效应变相较于不考虑时提升幅度约为2.6%;Ⅱ型推进剂药柱的最大等效应变提升幅度约为13.7%。

(a)Type Ⅰ propellant grain (b)Type Ⅱ propellant grain图16 药柱等效应力沿路径1~3变化图Fig.16 Equivalent stress varies along the Path 1~3

(a)Type I propellant grain (b)Type II propellant grain图17 药柱等效应变沿路径1~3变化图Fig.17 Equivalent strain varies along the Path 1~3
综上所述,推进剂力学性能分布不均匀性对药柱在点火增压下的力学响应有较大的影响。模量与损伤应变阈值的非均匀分布是影响应力-应变响应的重要参数。局部区域的损伤应变阈值降低缩短了推进剂应力-应变曲线中模量较高的线弹性阶段,等效降低了推进剂的模量,因此导致药柱应力响应降低,应变响应增大。
3.4.2 药柱损伤评估
为分析推进剂力学性能非均匀性对药柱损伤特性的影响,定义损伤系数ω为药柱等效应变与损伤应变阈值之比,即ω=εeq/εth。当ω≥1时,药柱出现损伤;当ω<1时,药柱未出现损伤。图18为药柱损伤系数ω沿路径1~3上的变化曲线图。
由图18可见,在点火增压载荷下,考虑推进剂力学性能非均匀性与否时,两型推进剂药柱在路径1上的损伤系数几乎没有差异,且除人工脱粘层根部和药柱后端位置外,损伤系数均小于1,即未出现明显损伤;但在药柱内孔中部,考虑推进剂力学性能非均匀性时,两型推进剂药柱的损伤系数均高于不考虑推进剂力学性能非均匀性时的损伤系数。
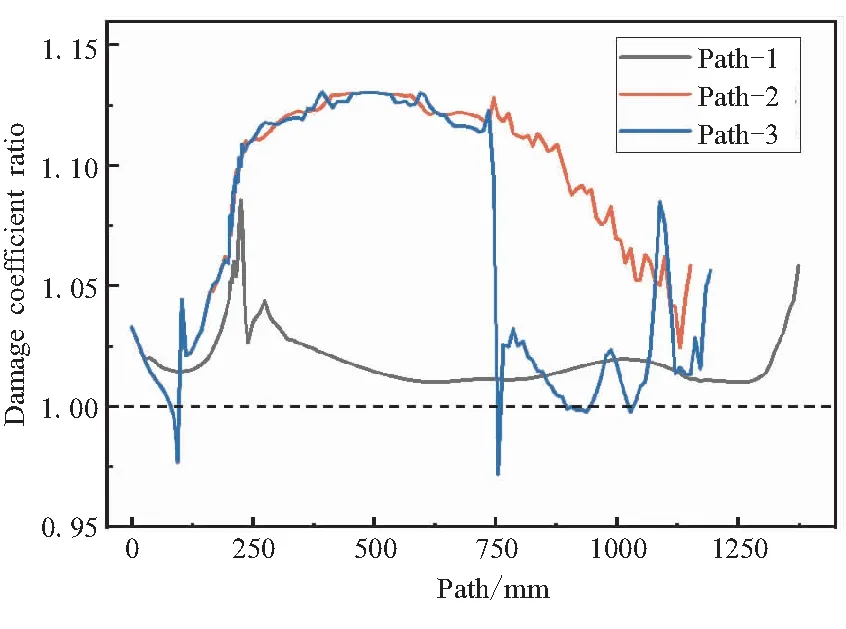
定义ηω为考虑推进剂力学性能非均匀性与否时损伤系数的比值,不同路径上的ηω值如图19所示。由图19可见,两型推进剂药柱在路径1上的ηω略大于1。但在药柱内孔中部,Ⅰ型推进剂药柱的ηω为1.13左右,Ⅱ型推进剂药柱的ηω为1.52左右。这是由于药柱在内孔中部的固化定应变较大,一方面两型推进剂的损伤应变阈值均随固化定应变的增大而减小;另一方面,对于Ⅱ型推进剂,其模量随固化定应变的增大而降低,从而使药柱内孔中部在点火增压载荷下的应变响应增大。两方面的原因使得两型推进剂的ηω大于1,且Ⅱ型推进剂药柱损伤系数的增幅明显大于Ⅰ型推进剂药柱。

(a)Type I propellant grain

(b)Type II propellant grain图18 损伤系数随路径1~3的变化规律Fig.18 Damage coefficient varies along the Path 1~3
(a)Type I propellant grain

(b)Type II propellant grain图19 损伤系数比随路径1~3的变化规律Fig.19 Damage coefficient ratio varies along the Path 1~3
3.4.3 药柱结构完整性评估
采用基于Von Mises应变准则的单一安全系数评估法对两种类型推进剂药柱在点火增压作用下的结构完整性进行评估,其表达式为
(26)
式中SF为药柱安全系数;[ε]为许用应变。
药柱泊松比为0.495~0.498,其等效应变与推进剂单轴拉伸时的延伸率近似相等,故而采用推进剂的单轴拉伸最大延伸率作为其许用应变[33]。
图20、图21分别为Ⅰ型和Ⅱ型推进剂药柱在点火增压完成时的安全系数云图。

(a)Considering the heterogeneity of propellant mechanical properties

(b)No considering the heterogeneity of propellant mechanical properties图20 Ⅰ型推进剂安全系数云图Fig.20 Safety factor contours of Type I propellant grain

(a)Considering the heterogeneity of propellant mechanical properties

(b)No considering the heterogeneity of propellant mechanical properties图21 Ⅱ型推进剂安全系数云图Fig.21 Safety factor contours of Type Ⅱ propellant grain
由图20、图21可知,药柱危险点均位于药柱内孔中部,考虑推进剂力学性能非均匀性时Ⅰ型推进剂药柱安全系数为3.14,不考虑时安全系数为2.32,前者相较后者提升幅度为35.34%;考虑推进剂力学性能非均匀性时Ⅱ型推进剂药柱安全系数为1.48,不考虑时安全系数为2.13,前者相较后者下降幅度为30.52%。由此可见,药柱力学性能的非均匀分布对其结构完整性有较大的影响。
药柱的安全系数直接受两方面因素的影响,一是药柱在点火增压载荷下的最大等效应变,二是推进剂的最大延伸率。采用因素分析法计算以上两因素对药柱安全系数的影响度,计算结果如表4所示。

表4 两型推进剂药柱安全系数影响因素分析Table 4 Analysis of influence factors on safetyfactor of two propellant grain
由表4可见,考虑推进剂力学性能非均匀性时,最大等效应变对Ⅰ型推进剂药柱的安全系数的影响度为-10.15%,对Ⅱ型推进剂药柱的安全系数的影响度为31.63%;最大延伸率对Ⅰ型推进剂药柱的安全系数的影响度为110.15%,对Ⅱ型推进剂药柱的安全系数的影响度为68.37%。由此可见,考虑推进剂力学性能非均匀性时的两型推进剂药柱安全系数变化主要由固化定应变引起的推进剂最大延伸率变化决定。
4 结论
针对推进剂药柱力学性能空间分布不均匀性问题,采用基于梯度有限元法的推进剂药柱结构完整性评估方法,基于HTPB推进剂在定应变载荷作用下的两类典型本构响应特性构建药柱力学性能非均匀场,据此分析药柱在点火增压载荷下的结构完整性,结论如下:
(1)模量与损伤应变阈值的非均匀分布是影响HTPB推进剂药柱力学响应的两个重要参数。损伤应变阈值随定应变的增大而减小,使得推进剂药柱在点火增压载荷下提前进入损伤状态,等效降低了推进剂的模量,因此导致两型推进剂药柱的应力响应降低,应变响应增大。
损伤应变阈值的降低缩短了推进剂应力-应变曲线中模量较高的线弹性阶段,等效降低了推进剂的模量,因此导致药柱应力响应降低,应变响应增大。
(2)相对常规结构完整性评估方法,考虑药柱力学性能非均匀性时,Ⅰ型推进剂药柱安全系数由2.32上升到3.14,上升幅度约为35.34%;Ⅱ型推进剂药柱安全系数由2.13下降到1.48,下降幅度为30.52%。药柱力学性能的非均匀分布对其结构完整性有较大的影响。
(3)考虑推进剂力学性能非均匀性时,药柱安全系数变化主要由推进剂最大延伸率变化决定。如最大延伸率对Ⅰ型推进剂药柱的安全系数的影响度为110.15%,对Ⅱ型推进剂药柱的安全系数的影响度为68.37%。

