沥青混合料探地雷达图像正演模拟与扩散研究

袁国庆,汤 文,吕悦晶,胡 菲

(1.武汉科技大学汽车与交通工程学院,湖北 武汉 430065)(2.武汉城建建设工程有限公司,湖北 武汉 430065)

近几十年,探地雷达(ground penetrating radar,GPR)作为一种效率高、样本大、检测快的无损检测仪器,虽然已被越来越多地应用于道路检测工程中,但仍存在缺乏异常图像客观评判标准、检测资料具有多解性和主观经验性的问题[1-2]。针对以上问题,笔者通过参与探地雷达检测项目,并研究了相关理论知识,利用基于时域有限差分算法的gprMax软件和扩散方程,对沥青混合料的探地雷达图像进行正演模拟,对探地雷达发射的电磁波扩散进行分析,获得了新电磁指标扩散率D和损耗σ,该指标可以用作表征沥青混凝土道路结构完整性的参数,并有助于建立探地雷达无损检测图像评判标准。

对比常规钻芯取样道路检测方法,本研究具有无损伤、效率高、检测能力更强、检测深度更深等优点[3-4]。同时,通过探地雷达无损检测,节约了物料成本,省时省力更精确[5-6]。在研究过程中,笔者试验了不同的观测值:相对介电常数、传播速度、衰减(振幅对数的斜率系数,能量衰减)、到达时间、直达波或反射波的峰值,此类数值参数均无法表征混凝土相关特性[7]。在研究一维到三维的扩散方程文献过程中,已经考虑了声波、电磁波和弹性波的近似扩散,研究的目的是可以在混凝土中模拟GPR波的扩散[8-9]。混凝土中存在大量成分、尺寸和形状各异的因素,波能受混凝土中散射的影响而在时间和空间上分散,因此信号由相干和不相干两部分组成[10]。

抵抗空间平均的相干部分是在有效介质中传播的波,表明介质的均质形式[11]。信号的不相干部分传播路径较为曲折,因此在一个波长尺度上显示了微结构的复杂性[12-13]。信号的不相干部分,在研究中被称为“尾波”[14]。相关文献中已使用超声波来检测混凝土中的损伤,但较少有研究电磁波的[15-17]。因此本文对电磁波在混凝土中的扩散进行了分析,在建立数值模型后,使用扩散方程的解析解对电磁波进行分析。通过分析获得的参数扩散率D和损耗σ的变化规律,可以作为电磁波参数建模的函数。

1 原理和方法

笔者首先使用gprMax进行二维建模工作,用软件基于时域有限差分算法(finite difference time domain,FDTD)模拟电磁波传播[18]。基于麦克斯韦方程组数值解的FDTD方法是离散空间和时间连续性的方法。因此,空间和时间的离散化步骤起着非常重要的作用,离散化的数值越小,FDTD模型越接近问题的真实情形。因计算机的存储量、处理速度有限,导致离散化步骤的值也是有限的。FDTD模型代表了实际问题的离散,且大小有限。离散化FDTD网格的构建块是以Yeane命名的Yee元胞,Yeane是FDTD方法的开创者[18],三维Yee元胞如图1所示。Yee元胞作为三维Yee单元的简化,较容易获得二维FDTD单元。通过为电磁场分量的位置分配适当的本构参数,可以在模型中包含复杂形状的目标。

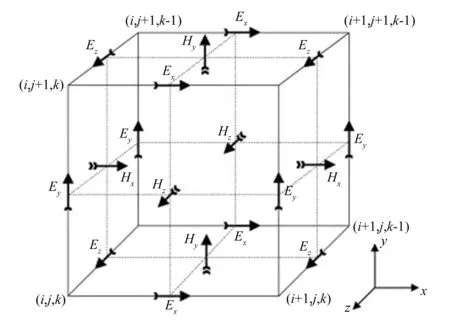
图1 Yee元胞

通过使用应用于每个FDTD单元的麦克斯韦卷积方程的离散版本,可以在时域中直接获得数值解。由于这些方程在空间和时间上均是离散的,因此可以用迭代的方式获得解。在每次迭代中,电磁场都会在FDTD网格中前进(传播),并且每次迭代都对应于一个经过的模拟时间Δt。因此,通过指定迭代次数,可以指示FDTD求解器模拟给定时间窗口的字段。

使用类似FDTD的显式数值直接在时域中获得解决方案,时间离散化步骤Δt的值与空间离散化Δx、Δy和Δz的值不能彼此独立地分配。以Courant、Freidrichs和Lewy首字母命名的稳定性条件称为CFL条件[18],该条件的表达式为:

式中:t为时间参数,由Δx、Δy和Δz的值限定;c为光速。通过设定Δz→∞,二维情况下的稳定性条件较容易获得。

2 正演模拟

2.1 gprMax和建模参数

使用gprMax进行二维正演模拟建模,图2显示了执行代码的模型几何形状。模型尺寸如下:x方向从左到右共计50 cm,y方向从下到上共计20 cm,包含5 cm自由空间(空气)与15 cm混凝土(由沥青混合料组成:沥青和骨料)。z方向垂直于x和y方向。完美匹配层(PML)以默认配置显示(10个单元的空间离散化dx=dy=dz=0.002 m)。电磁(EM)源和接收器采用面对面的“传输”配置,其中源信号是电激励(赫兹偶极子),由在z方向极化的电流密度表示。因此,激励电磁波形与此激励相关。电磁源和接收器之间的距离固定为15 cm,扫描步长为5 mm,从左到右共计84次A扫描。

图2 沥青混凝土的gprMax 2D模型

对2组碎石集料进行建模:1)半径为5～20 mm的细集料;2)半径为20～40 mm的粗集料。这些粗细集料随机分布在模型中,每种尺寸的骨料数量用图3和图4中的累计百分比表示,集料的密度为2 600 kg/m3。细集料的相应体积分数为0.31,粗集料的相应体积分数为0.42。

图4 粗集料的累计质量百分比

此外,电磁源信号的3个频率分别为1.5、2.6和4.0 GHz;不同种类材料的介电常数均不相同,参见《常见物质介电常数表》[17],集料和沥青之间的相对介电常数根据材料种类不同分别为εa=5、εm=7,εa=5、εm=13和εa=7、εm=13。在测试时,集料和沥青的电导率被认为是恒定的,为0.02 S·m-1。集料和沥青的相对磁导率和磁损耗均是恒定的,分别为1和0 Ω/m。

2.2 电磁波扩散

本文中沥青混凝土道路无损检测采用的是探地雷达仪器,该仪器是通过自身的发射天线向地下探测物发射高频电磁波,电磁波在地下介质中传播时遇到存在电性差异的分界面会发生反射,然后通过接收天线来接收反射回地面的电磁波,根据接收到的电磁波的波形、振幅强度和时间的变化等特征推断地下介质的空间位置、结构、形态和埋藏深度等。混凝土样品中电磁波的扩散可通过以下扩散方程建模[19]:

E0δ(y)δ(t)

(1)

式中:D为扩散率,是材料微观结构的特征,取决于集料的密度、几何形状和平均间距[20],m2/s;E(y,t)为位置y和时间t处的能量,J;∂t为时间t处的偏微分,s;σ为损耗,对于弹性波,它表明了介质的黏弹性,与用于混凝土的沥青的性质有关,s-1;E0为时间t=0时源处的初始能量,J;δ(y)为y向电场场强,V/m;δ(t)为电场场强损耗,V/m。对于电磁波,σ与电磁损耗(介电常数的虚部)有关。δ是Kronecker符号。

公式(1)的解为:

(2)

式中:C0为初始能量,ys为源与接收器之间的距离,Dt为扩散率。

在本文中,公式(2)将用于拟合通过gprMax获得的GPR信号。步骤如下:首先计算每个A扫描(总共84次);然后计算相干信号,该信号是所有A扫描的平均值,从每个Ascan中减去该相干信号,就可获得每个Ascan信号的不相干部分(尾波)。从所有Ascan计算出平均能量,通过矩阵求逆,计算出该能量的自然对数,并与扩散方程的解析解拟合,推导扩散率D和损耗σ[21]。拟合的精度用归一化均方根偏差(NRMSD)表示,使用gprMax的最大值减去最小值进行归一化[22]。

3 数值分析

首个Ascan的不相干信号如图5所示,用于在x方向上极化的磁场,在4 GHz时细集料的相对介电常数为Δεa=7、Δεm=13。

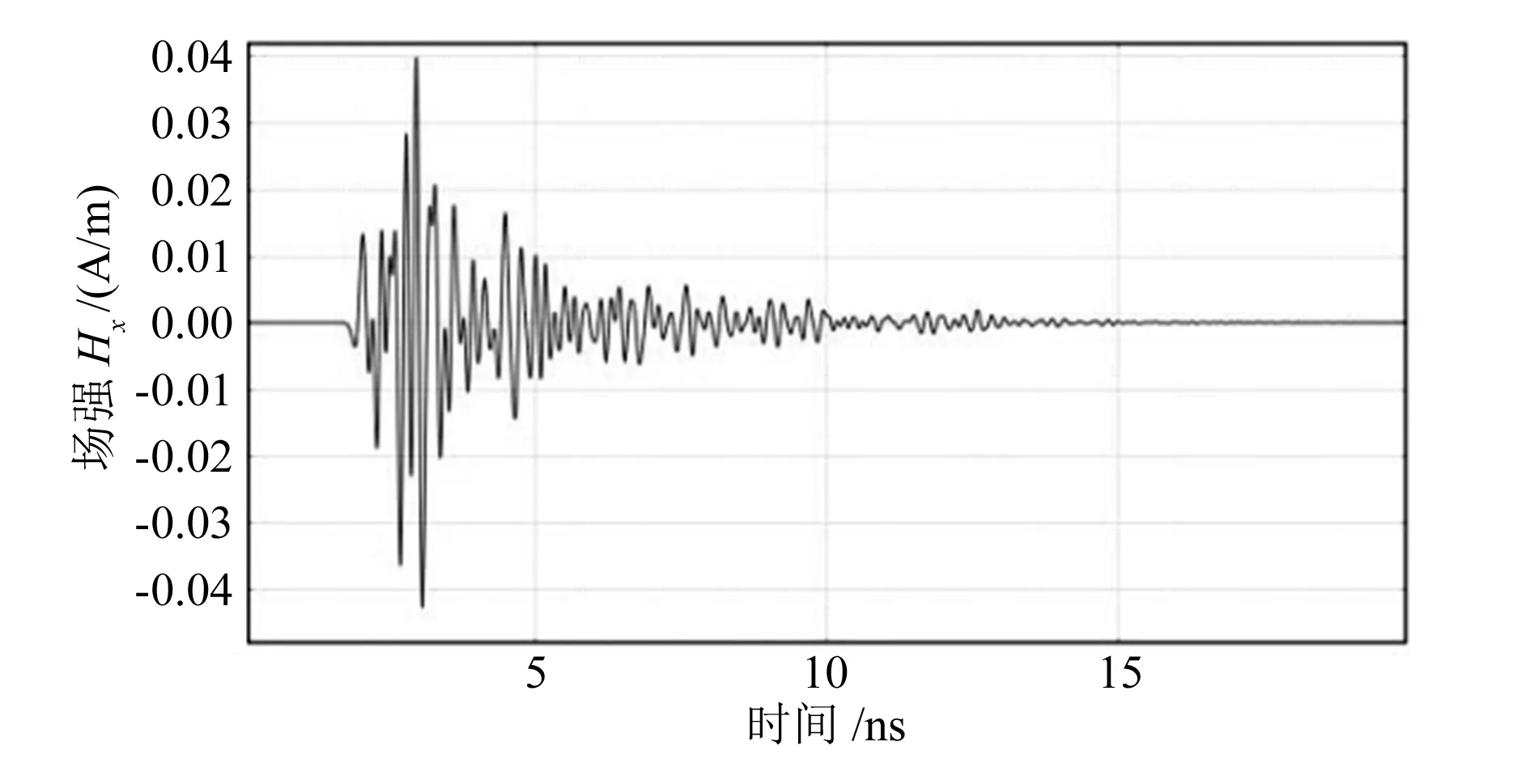
图5 在第一个Ascan处沿x方向极化的磁场的不相干部分

根据前文描述的过程,从所有扫描中计算出能量的平均值,并用公式(2)进行拟合,如图6所示。D=7.06E+07 m2/s和σ=7.63E+08 s-1是从细集料的拟合中得出的,在4 GHz时的相对介电常数为Δεa=7、Δεm=13。

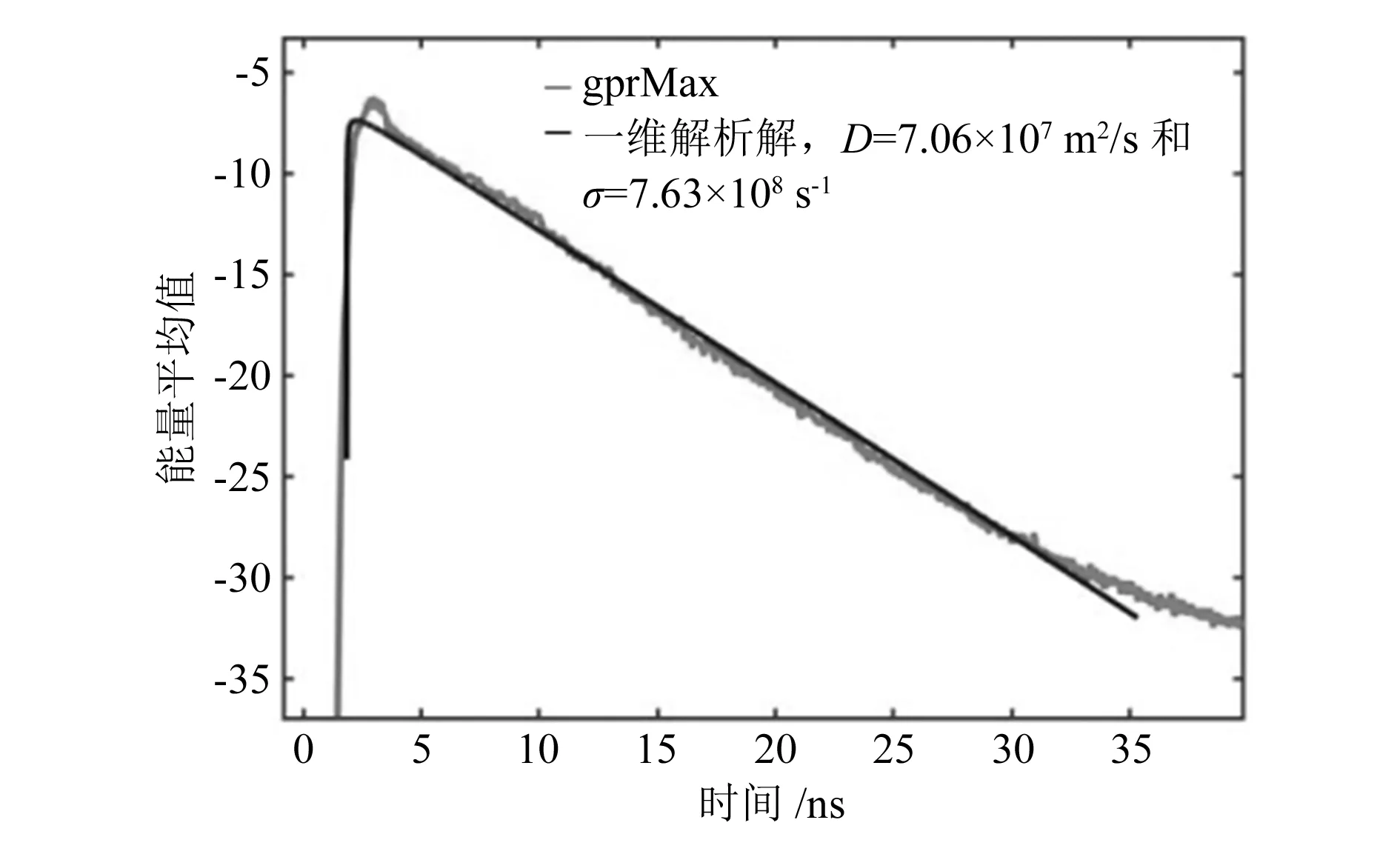
图6 用gprMax给出的解拟合扩散方程的解析解

对所研究的参数重复上述过程,获得NRMSD范围为1.6%～4.2%的D值和σ值。

图7展示的是从粗、细集料获得的D值的比较,其中Δεa=7、Δεm=13。在频率为1.5 GHz时,粗集料的D值高于细集料;在频率为2.6 GHz和4.0 GHz时,细集料的D值高于粗集料。用相对介电常数和波长的综合作用可以解释这一观察结果。实际上,当相对介电常数为5、频率为1.5GHz时,计算出的波长为9.0 cm;当频率增加到2.6 GHz和4.0 GHz时,波长分别减小到5.2 cm和3.4 cm。当相对介电常数为13,频率为1.5、2.6和4.0 GHz时,波长分别为5.5、3.2和2.1 cm。扩散率D表明所传播能量的路径越曲折,行进长度和扩散率将越高。

图7 从粗、细集料获得的D值比较

图8为在Δεa=7、Δεm=13的情况下,从粗、细集料获得的σ值的比较。结果显示,粗集料的σ值随频率的变化均大于细集料。损耗σ与电磁衰减(介电常数的虚部)有关,在后续的工作中,可研究其随集料和沥青电导率的变化规律。

图8 相对介电常数Δεa=7、Δεm=13的σ值比较

图9所示为考虑3种相对介电常数的D值的比较情况。结果表明,当相对介电常数为Δεa=5、Δεm=7时,D值随着频率升高而降低。在其他相对介电常数时,D值基本无影响。此外,以1.5 GHz的频率计算相对介电常数分别为7和13所对应的混凝土中电磁波的传播速度,相对介电常数为7比相对介电常数为13对应的混凝土中电磁波的传播速度提高了1.3倍。同理,在频率为1.5 GHz时,扩散率D在相对介电常数Δεa=5、Δεm=7对应的混凝土中电磁波的扩散率比Δεa=5、Δεm=13对应的混凝土中电磁波的扩散率提高了20倍。在考虑相对介电常数对比的情况下,D的灵敏度在1.5 GHz时比通常电磁波传播速度提高了20倍。

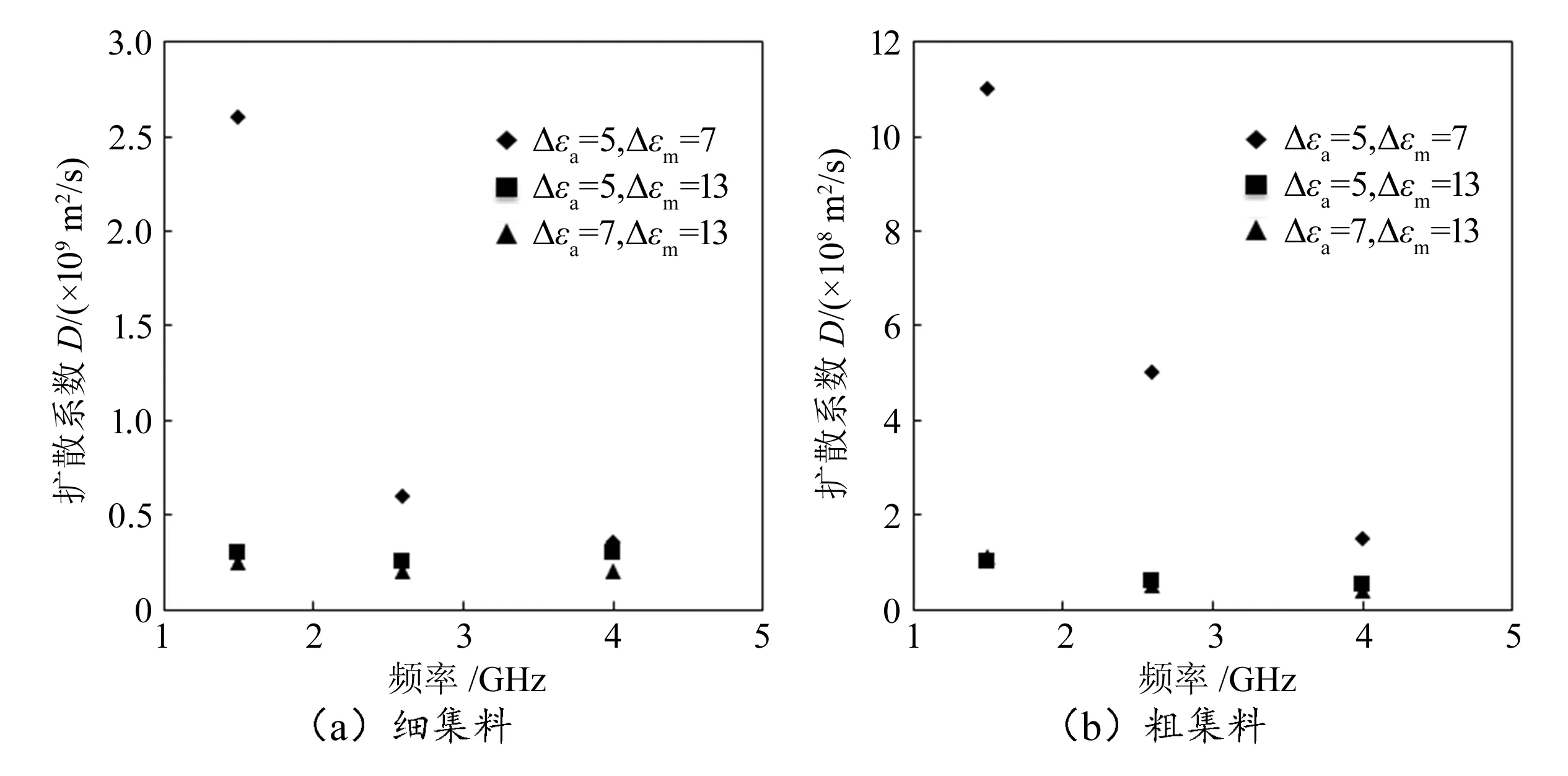
图9 3种介电常数的D值比较

图10所示为粗、细集料在3种相对介电常数时的σ值比较情况。结果显示,无论粗、细集料,在相对介电常数分别为Δεa=5、Δεm=13和Δεa=7、Δεm=13时,σ值随频率的降低而降低。相对介电常数为Δεa=5、Δεm=7时,σ值没有明显变化。

图10 3种介电常数的σ值比较

在频率为2.6 GHz时,相同条件下,相对介电常数分别为Δεa=5、Δεm=7和Δεa=5、Δεm=13时,前者比后者电磁传播速度提高了1.3倍,σ增加了6倍。

4 结束语

由文中描述可知:1)沥青混合料探地雷达图像正演模拟具有可行性。2)损耗σ和扩散率D可以作为表征混凝土结构完整性的新指标。理想情况下,该参数分别比常用的电磁传播速度敏感6～20倍。3)损耗σ和扩散率D可以通过电磁波在混凝土中的多次扩散进行建模而获得。D和σ对测量频率、集料大小以及集料与沥青之间的相对介电常数比较敏感。多数情况下,D和σ随频率升高而降低。

未来笔者将会重点考虑电导率、磁导率以及沥青混合料的三维建模工作,并计划通过实验测量,将这些研究应用到工程实际中。