基于机器学习的风力发电变桨系统自适应容错控制方法

郑小春,李 明,黄志星,王明辉,邱建培

(华电福新发展有限公司福清分公司,福建 福州 350300)

为保证风电机组本身的安全,提高风力发电能力,降低发电成本,需优化风力发电变桨系统,即在提高发电功率的同时,进行容错控制,避免功率越过安全线的现象[1]。

文献[2]通过干扰输入与输出的系统参数,设计了一种基于二元参数估计的故障诊断系统,并对系统中的容错控制进行自适应估计,但该容错控制系统没有将系统错误传递到传感器中,导致参数输入的步骤存在缺陷。文献[3]将风力发电机组变桨系统中的力学特性作为容错控制的检测端口,并通过该端口进行故障的容错对比,得到了安全、稳定的容错控制方法,然而这种方法难以计算不断变化的系统参数,仅能作为一种事后检验容错系统的机制,而不能作为一种实时计算和调整的容错控制方法。文献[4]通过滤波器的残差与加速度系统中的信号建立了一个自动保护装置,同时进行了容错控制,该装置能够实现容错控制的自适应,但是需要多个传感器共同工作,整个系统的运行十分不稳定。文献[5]针对双馈式风电机组存在的故障,提出模型参考自适应的鲁棒容错控制方法,在执行器不同健康情况下较好地完成了跟踪任务,但控制过程中存在无法计算时间常数比值的问题。文献[6]针对具有随机非线性和不确定性的网络化控制系统,引入自适应事件触发通讯机制,给出自适应事件触发通讯机制与鲁棒容错控制器的协同设计方法,控制性能良好,但向量函数的误差计算过程不明确。文献[7]建立级联式无刷双馈发电机的数学模型,通过矩阵分离,避免时变系统复杂的极点配置问题,提高级联式无刷双馈风力发电系统的可靠性,但是风力发电系统的真实控制效率较差。

以往的研究中,由于自适应学习过程存在容错元参数与网络拓扑选择困难的问题,将其应用于容错控制方法中,容易陷入上述众多困境,即引发误差计算错误、不能自动容错的问题,而在机器学习的自适应滤波算法中,引入模糊逻辑,构建容错控制自适应逼近模型,即可高效完成风力发电变桨系统的自适应容错控制方法设计。

1 风力发电变桨系统容错控制方法

1.1 计算控制器跟踪误差

在设计风力发电变桨系统的容错控制方法之前,需要计算该控制器的跟踪误差。设控制器的状态方程为:

(1)

式中:xn为状态趋近于0的节点,n=1,2,3,4;Tx(h)为控制器在反向操作过程中所需要的时间;Ty为控制器在正向操作过程中需要的时间;μc,μb分别为风力发电变桨控制器的正向跟踪误差系数、反向跟踪误差系数;Hu为控制器的误差变量[5]。通过式(1),可得跟踪误差的导数计算公式:

(2)

式中:f1、f2、f3、f4为坐标值导数系数,α1、α2、α3、α4均为约束条件下控制器误差变量参数。将增益参数λy作为控制器跟踪误差的上界,减损参数λx作为控制器跟踪误差的下界,通过对称矩阵的计算,得到未知函数的输入节点逼近。为了简化计算过程,定义一个向量矩阵Xu:

(3)

式中:Xu为功率计算过程向量矩阵,Xi为第i个风力发电机组功率,Hu为第u个虚拟控制器的跟踪误差矩阵,θx为误差系数[6-8],n为补偿系数个数。通过式(1)～(3)可得控制器的跟踪误差。

1.2 基于机器学习的容错算法

将控制滤波作为放射器,计算风力发电变桨系统控制过程的补偿误差:

(4)

式中:λn(x)为系统控制器的补偿误差,n=1,2,3,4;Xn(d)为系统控制器的跟踪误差,n=1,2,3,4;gmd(z)为控制器设定的初始信号,m=2,3,4[9]。通过初始信号,求得输出信号与补偿信号的模型结构,设置输出信号频率阈值函数:

(5)

式中:λn(x+1)表示当补偿误差的定义域较以往更大时,第n个系统误差的补偿系数;Xn(d-1)表示当跟踪误差较以往更小时,第n个系统的跟踪系数;Vyn为机器学习的正向轨道中第n个参考值的个数。设置补偿信号的频率阈值函数:

(6)

式中:λn(x-1)表示当补偿误差的定义域较以往更小时,第n个系统误差的补偿系数;Xn(d)表示与以往相同的跟踪误差系数;Vxn为机器学习的反向轨道中第n个参考值的个数。

假设容错算法得到的数据是一个常数,则可以定义风力发电系统的真实控制率为:

(7)

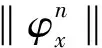
1.3 建立风力发电变桨系统容错控制自适应逼近模型

考虑风力发电变桨系统的动态性,将其视作一个四阶动态系统,当系统的状态为零时,将式(8)代入状态方程即式(1)中,计算其容错逼近值。

(8)

式中:hi为定位后的故障节点偏离参数。通过以上模糊逼近逻辑,进行基向量函数的误差计算,在此过程中,需要保证以下条件成立:

(9)

式中:g(x)、f(y)分别为基向量函数与权向量函数的逼近误差,μi为光滑函数中的参数特征。将式(9)作为判定依据,可以得到风力发电变桨系统容错控制自适应逼近模型,如图1所示。

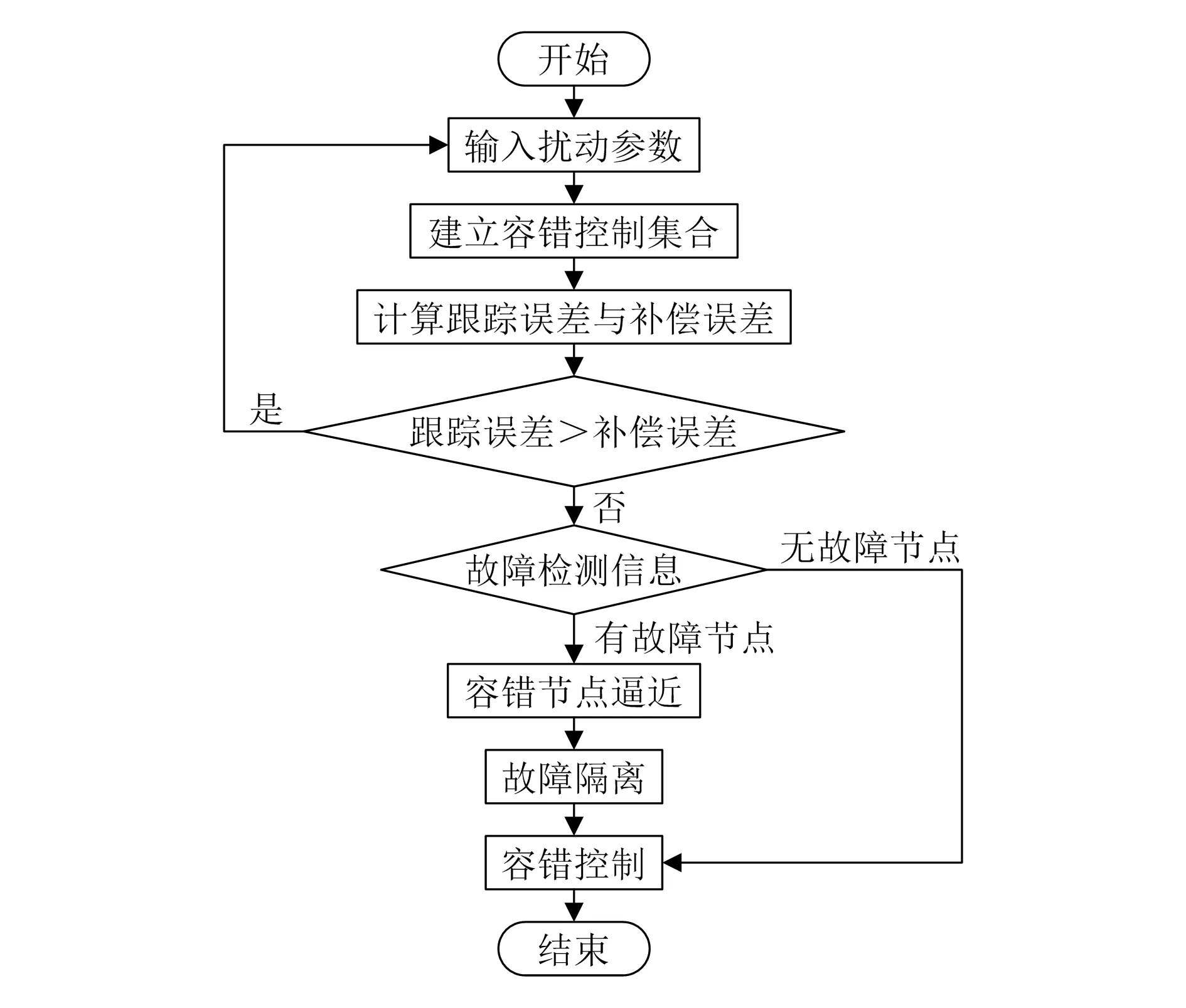
图1 容错控制自适应逼近模型

由图可知,输入扰动参数的根本目的在于计算出适当的跟踪误差与补偿误差,通过建立容错集合的方法,将集合中的两个误差进行对比,然后设置故障信息检测周期,通过式(8)和式(9)得到容错节点逼近的数据结构,进而实现风力发电变桨系统容错控制自适应逼近模型的构建。

2 数值研究

2.1 实验准备

为验证本文设计的自适应容错控制方法的可行性与优越性,将该方法与常规的3种方法即文献[2]方法、文献[3]方法和文献[4]方法进行对比。

分析功率的变化趋势,获取容错控制数据,设定3个机组,作为自适应容错控制实验的初始参数,以360 s为一个机组功率变化周期。其中,机组A包括两个功率峰值阶段与一个功率均衡阶段,机组B包括两个功率峰值阶段和两个功率均衡阶段,机组C包括一个功率峰值阶段与一个十分漫长的功率均衡阶段。假设风力发电变桨系统在运行过程中的信号统一为:

(10)

式中:ω为定义域参量,k为工况调节系数。

在该系统中,信号发射周期可以表示为:

TΔx=0.035 4Kf

(11)

式中:TΔx为所有机组x的平均发射周期,Kf为系统状态的初始值。多次调试后,通过公式(3)计算出风力发电机组在时间流逝下的功率变化。

2.2 不同机组系统容错效果测试

将文中设计的自适应容错控制方法作为实验组,将文献[2]方法、文献[3]方法和文献[4]方法作为3个对照组,以功率变化作为依据,分别计算不同方法在3个机组中的容错效果,如图2所示。

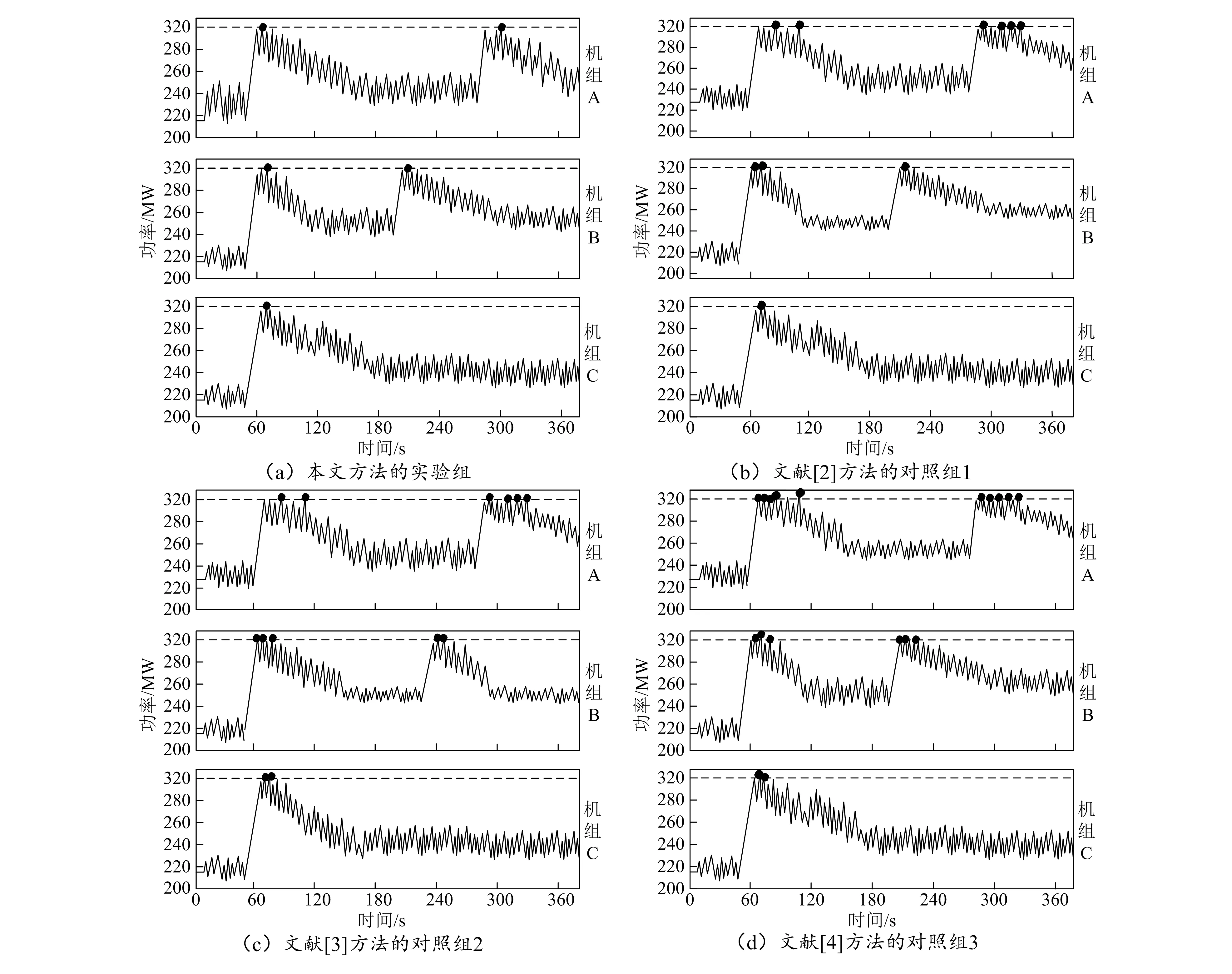
图2 不同机组下系统容错效果

图2中,功率随着时间变化,先上升至临界值,

然后降到合适的范围。4种方法均没有完全将功率控制在临界值以下,将超出临界值的部分在图中全部用实心的圆圈标出。

由图2可知,实验组在机组A的实验中有2次(1+1)超出了临界值,在机组B中有2次(1+1)超出了临界值,在机组C中有1次超出了临界值。

为了保证实验结果的准确性,将以上实验全部重复15次,并取15次实验中功率峰值超过320 MW的次数作为本次实验的最终结果。功率超出临界值次数的计算结果见表1。

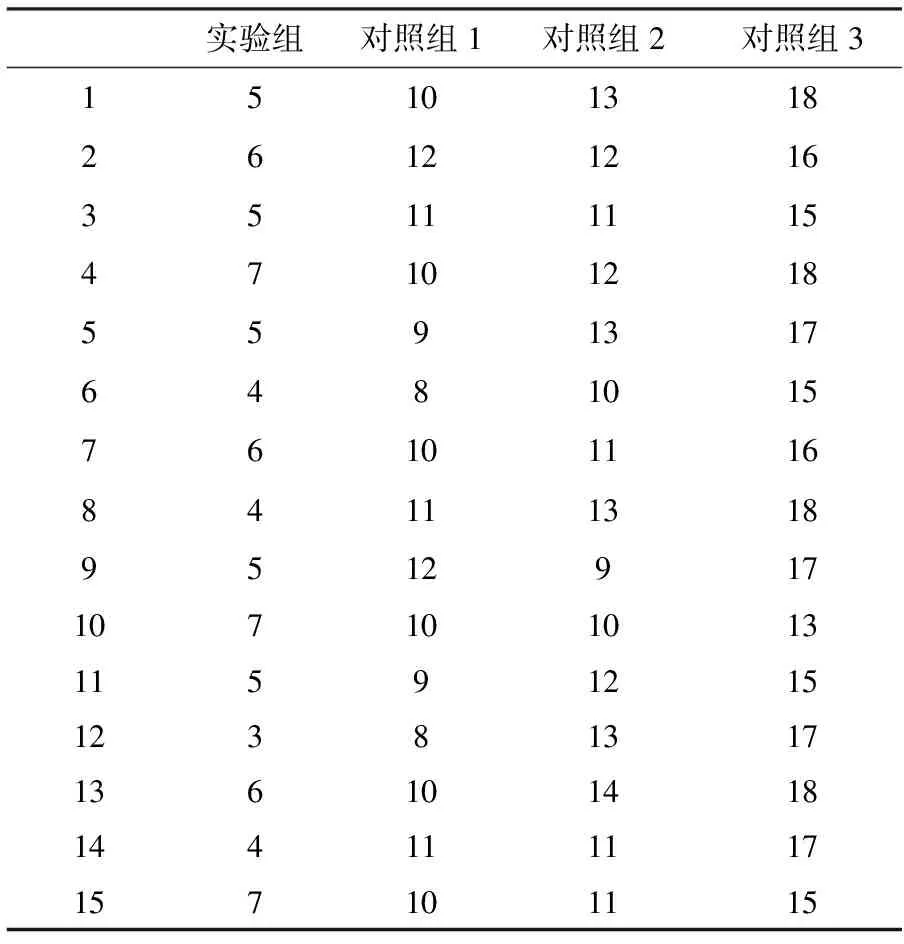
表1 功率超出临界值次数

由15组测试结果可知,实验组功率超出临界值的总次数为74,对照组1功率超出临界值的总次数为141次,对照组2为162次,对照组3为227次,说明应用本文方法后,风力发电变桨系统功率控制过程的鲁棒性较高。

3 结束语

为解决容错控制中跟踪误差与补偿误差计算失误的情况,本文采用机器学习的方法,建立控制模型,得到了准确度更高的模型,避免了系统重构过程中出现灵活性失稳的现象,及时推动了系统的实时分配,保证了期望目标的实现,这种方法具备极大的现实意义,为以后其他相关研究奠定了基础。