基于MOGA的焊接机器人龙门架结构优化研究
潘春玲
(潍坊科技学院智能制造学院,山东 潍坊 262700)
随着人工智能和自动化技术的普及,焊接机器人被广泛应用于航天航空、汽车制造等领域。目前,具有代表性的焊接机器人有加拿大设计的MWR-100/350E焊接机器人、德国亚琛工业大学研发的柔性铰链连接磁性驱动轮焊接机器人以及中国中铁建设集团与清华大学联合设计的轨道式焊接机器人等,其中我国设计的焊接机器人可灵活、自主地进行焊接。然而,由于焊接任务和焊接对象的不同,现有的焊接机器人在焊接质量和焊接效率方面仍有提升空间,因此许多学者对焊接机器人工艺参数进行了优化,如王林等[1]将热弹塑性有限元法和固有应变法相结合对焊接工艺进行优化,最大程度减小了焊后变形量;梁超等[2]结合神经网络和遗传算法对铝合金激光摆动焊接工艺参数进行优化,提高了焊接效率;李冉等[3]以低碳钢板材V型坡口对接平焊为研究对象,在建立有限元模型的基础上,采用遗传算法对模型进行最优求解,提高了V型坡口对接平焊的焊接效率。上述研究表明,对焊接机器人工艺参数进行优化可提高焊接质量和焊接效率,但焊接质量不仅与焊接工艺参数有关,也与焊接机器人结构有很大关系。为此,本文以焊接机器人龙门架结构为研究对象,提出一种基于多目标遗传算法(multi objective genetic algorithm,MOGA)的焊接机器人龙门架结构优化方法,并对该方法的可行性进行验证。
1 焊接机器人龙门架结构有限元分析
结合焊接机器人龙门架结构特点,基于SolidWorks软件构建龙门架有限元模型,如图1所示[4]。本文构建的焊接机器人龙门架的材料密度为7.85×103kg/m3,弹性模量为2.1×1011Pa,泊松比为0.3,屈服强度为235 MPa,采用平面壳体单元Shell181模拟,将有限元模型划分为57 862个节点、185 454个单元。
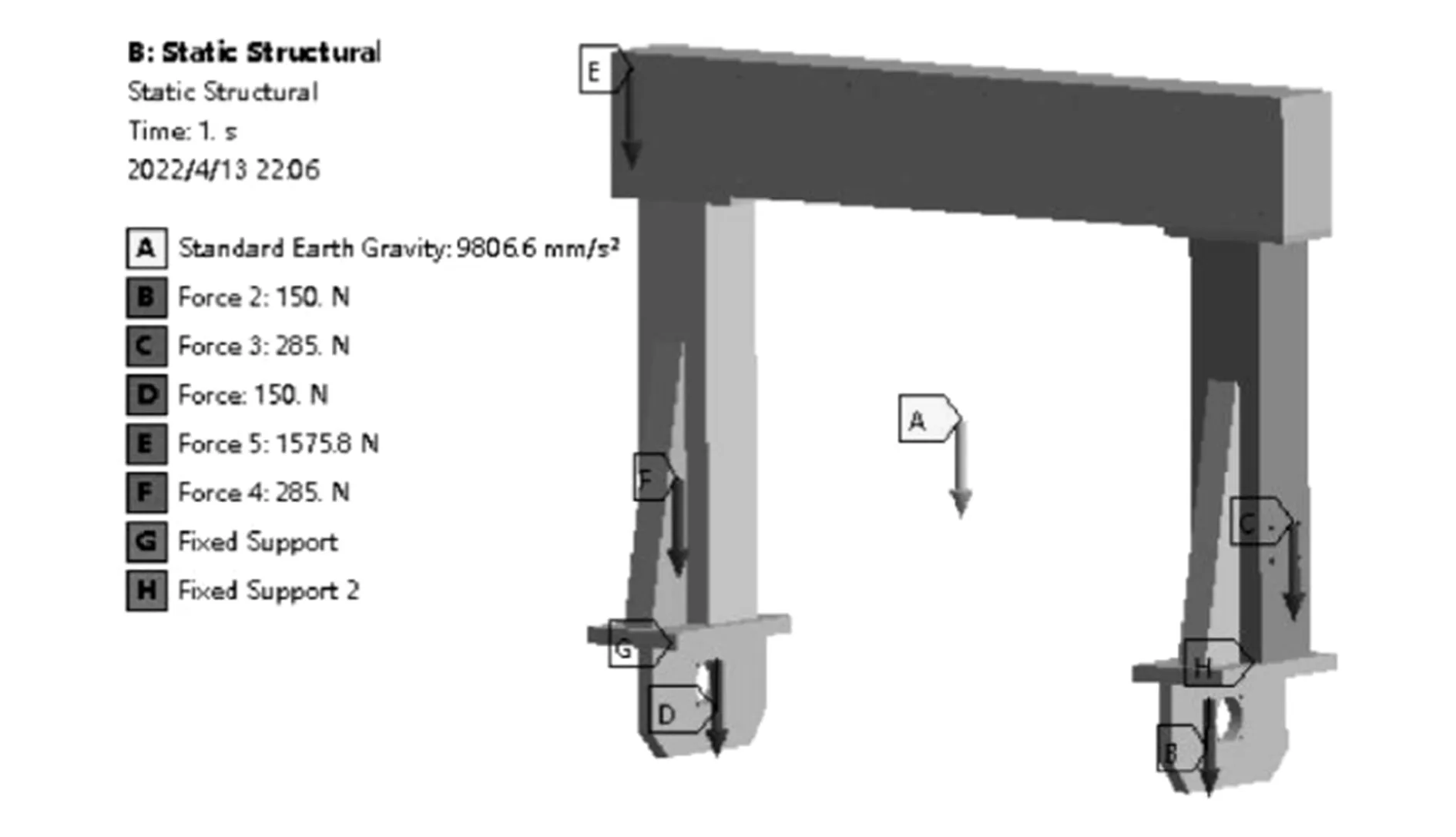
图1 焊接机器人龙门架有限元模型
考虑到直接对焊接机器人龙门架有限元模型进行优化会耗费大量的时间成本,为提高优化效率,结合焊接机器人龙门架结构非线性特点,采用Kriging模型构建焊接机器人龙门架结构近似模型。Kriging近似模型采用相关函数的方式对输入与输出变量进行表示,具体数学表达式为[5]:
Y(P)=yT(P)·β+Z(P)
(1)
式中:Y(P)和yT(P)分别为近似模型和全局模拟的回归计算模型,β和Z(P)分别为回归系数和分布误差。
2 焊接机器人龙门架结构优化
基于上述Kriging近似模型,为实现龙门架结构优化,首先确定龙门架结构待优化的设计变量,然后确定优化目标函数,最后选用合适的优化算法进行求解。
2.1 龙门架结构变量
焊接机器人龙门架由3个部分组成,分别为横梁、左/右立柱、立柱基座。为更好地分析龙门架结构与各组成部分的关系,选用横梁板材厚度(P1)、左/右立柱板材厚度(P2/P3)、立柱连接板厚度(P4)、底座板厚度(P5)、电机连接板厚度(P6)作为设计变量进行优化。龙门架结构横梁和立柱的横截面及变量参数位置标注如图2所示[6]。
2.2 龙门架结构优化目标函数构建
焊接机器人龙门架结构优化的目的是使龙门架结构总体质量最轻,因此以龙门架结构总质量P7作为优化目标,以P1~P6作为输入变量。同时考虑到最大静变形量(P8)、最大等效应力(P9)、1阶模态频率(P10)是决定龙门架结构性能的重要指标[7],因此以P8~P10为约束条件。结合以上分析,得到焊接机器人龙门架架构优化的目标函数如式(2)所示。
(2)
式中:fmax、σ、s分别为焊接机器人龙门结构最大静变形量、最大等效应力、隔振频率,本文取值于参考文献[8],设置为1.47 mm、236.67 MPa、47.14 Hz;PL、PU分别为设计变量下限和上限值。
2.3 龙门架结构优化目标函数求解
2.3.1MOGA
MOGA是以遗传算法(genetic algorithm,GA)为基础,采用Pareto最优个体对种群中所有个体进行排序,并根据排序结果使排名靠前的Pareto最优个体拥有更多机会遗传到下一代的一种多目标优化算法[9]。MOGA中Pareto排序就是对所有Pareto个体分配相同的复制概率,具体排序过程为:向当前种群中非支配个体分配次序为1,并从竞争者中将其移除,任何其他个体所分配的次序数等于支配该个体的数量加1[10-11]。如图3所示,首先根据个体次序对种群进行排序,当次序相同时,随机选取顺序;然后从最优个体到最差个体顺序根据线性或非线性差值的结果分配适应值,次序相同的个体适应值相同;最后,当种群中所有个体均分配到次序时,结束Pareto排序。
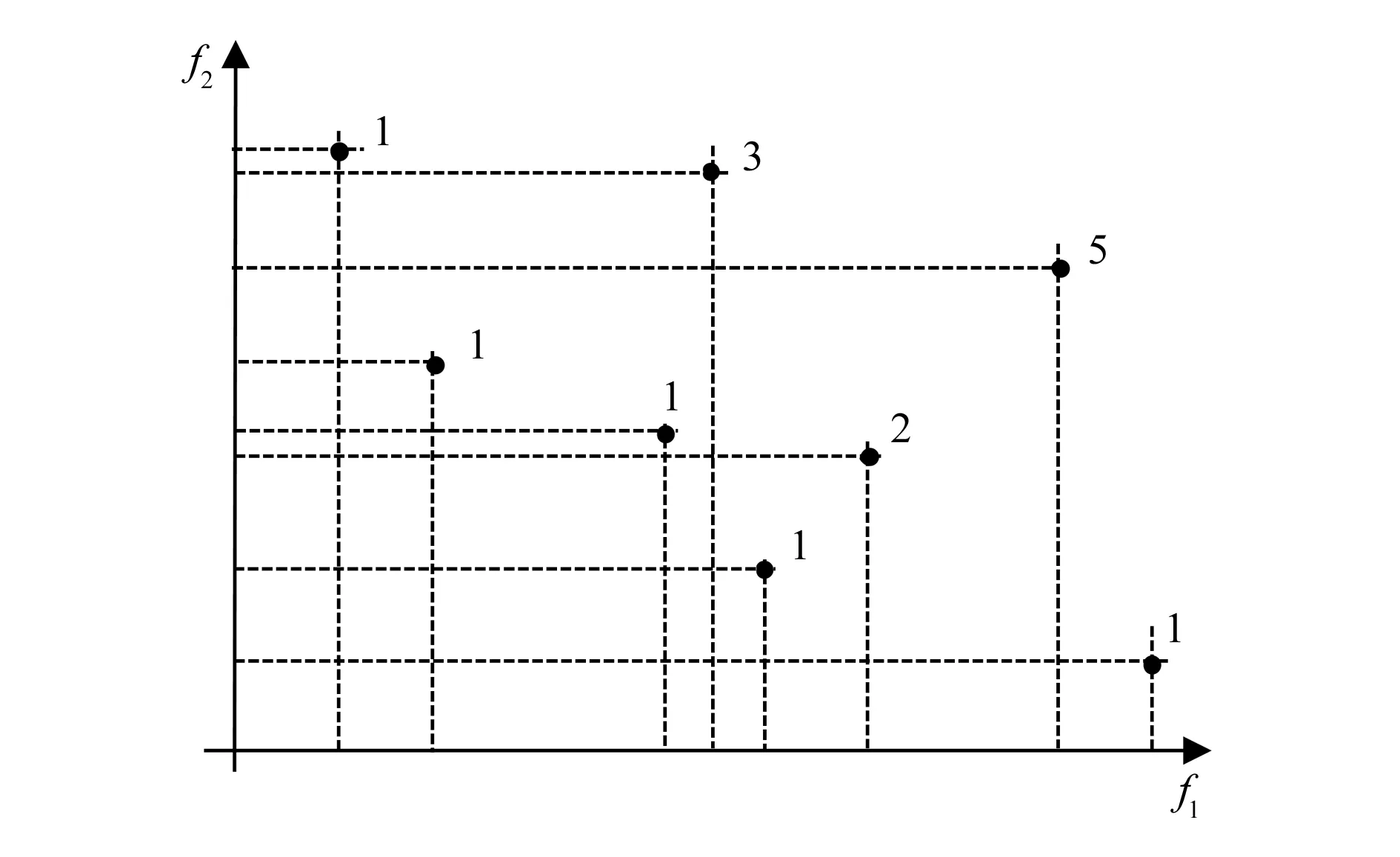
图3 Pareto排序方法
2.3.2龙门架结构优化求解流程
在构建龙门架结构有限元模型与Kriging近似模型、确定龙门架结构优化设计变量与目标函数的基础上,运用MOGA进行优化求解,步骤如图4所示。
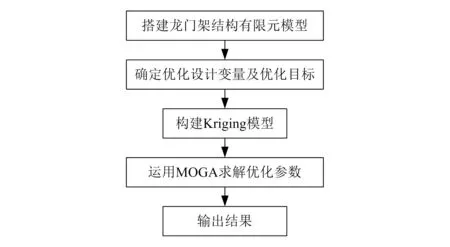
图4 焊接机器人龙门架结构参数求解流程
3 仿真分析
3.1 仿真环境搭建
本次仿真采用SolidWorks三维建模软件搭建焊接机器人龙门架结构有限元模型,运用ANSYS软件进行分析。系统配置为Intel 酷睿i7-9750H CPU 2.6 GHz,16 GB内存,Windows10操作系统。
3.2 数据来源及预处理
本次仿真数据为由拉丁超立方采样方法获得的焊接机器人龙门架三维模型结构数据[12]。焊接机器人龙门架结构参数P1~P6为输入变量,P7~P10为响应值。自定义样本和随机生成器种子数量分别设置为100和10,通过拉丁超立方采样方法获得P1~P10样本数据,见表1。
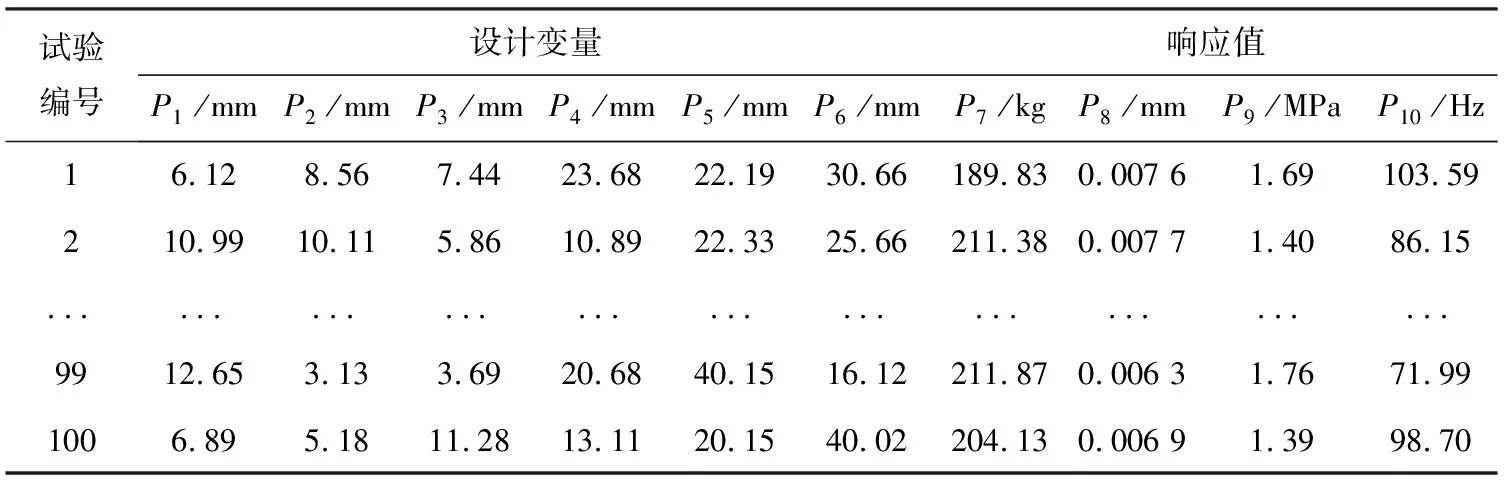
表1 P1~P10样本数据示例
3.3 参数设置
为了获得更好的实验效果,将MOGA初始样本点数量和参与迭代的样本点数量均设置为300,最大迭代次数设置为20,最大允许帕累托百分比和收敛稳定性分别设置为70%和2%[10]。
3.4 结果与分析
3.4.1Kriging近似模型精度验证
Kriging焊接机器人龙门架结构近似模型的精度直接影响焊接机器人龙门架结构优化目标的实现。图5为所构建的Kriging焊接机器人龙门架结构近似模型。由图5可知,构建的焊接机器人龙门架结构Kriging近似模型响应面轮廓边界明显,接近实际模型,说明所构建的Kriging近似模型具有一定的精度,可用于后续对焊接机器人龙门结构的优化分析。
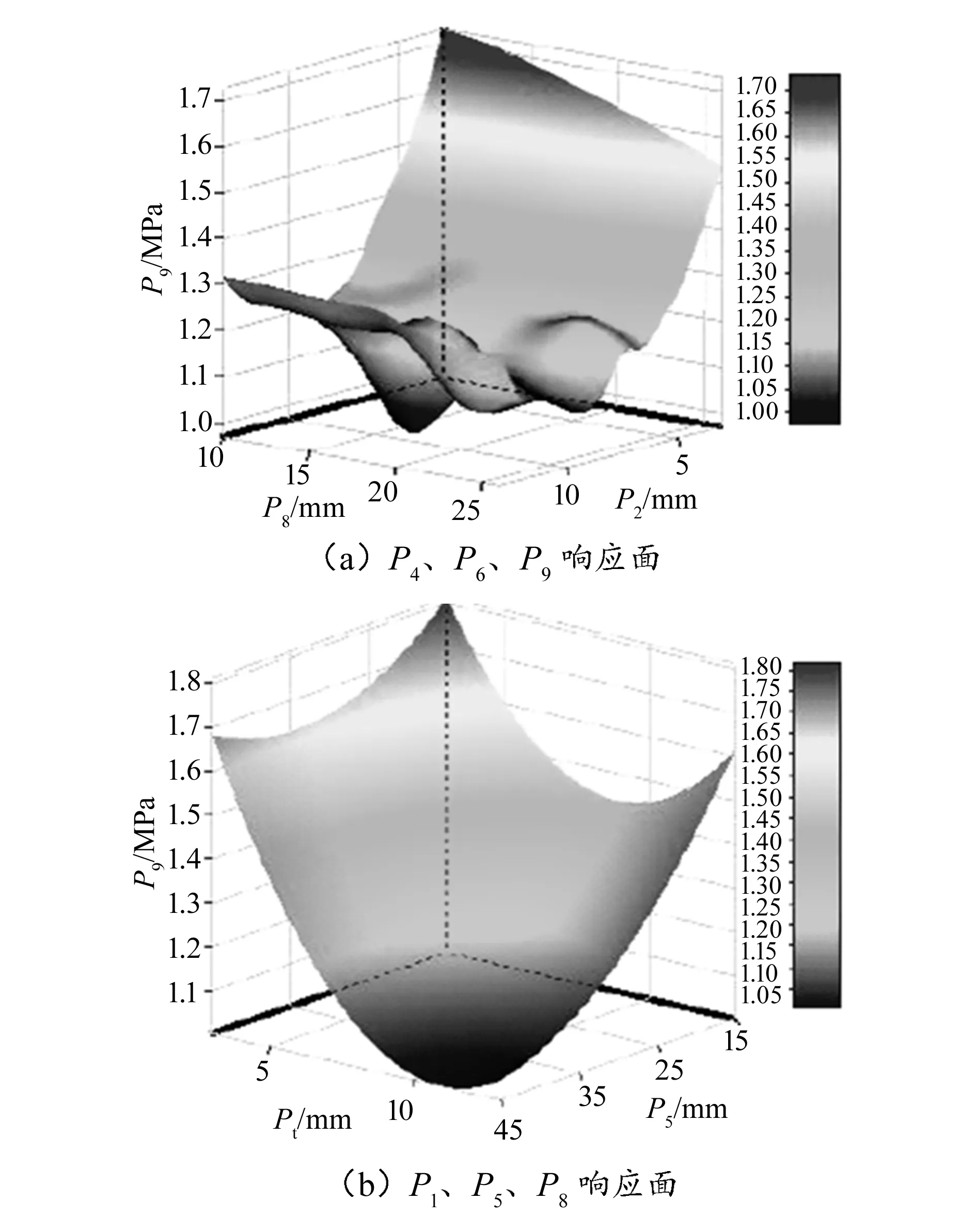
图5 Kriging近似模型
为定量分析所构建的焊接机器人龙门架Kriging近似模型的精度,实验选用可决系数R2、相对均方根误差(root mean square error,RMSE)和相对最大绝对误差(relative maximum absolute error,RMAE)来评估模型的拟合精度,结果见表2。由表2可知,所构建的焊接机器人龙门架Kriging近似模型参数P7~P10的R2值均为1,相对均方根误差和相对最大绝对误差均为0,说明Kriging近似模型具有优异的拟合精度。
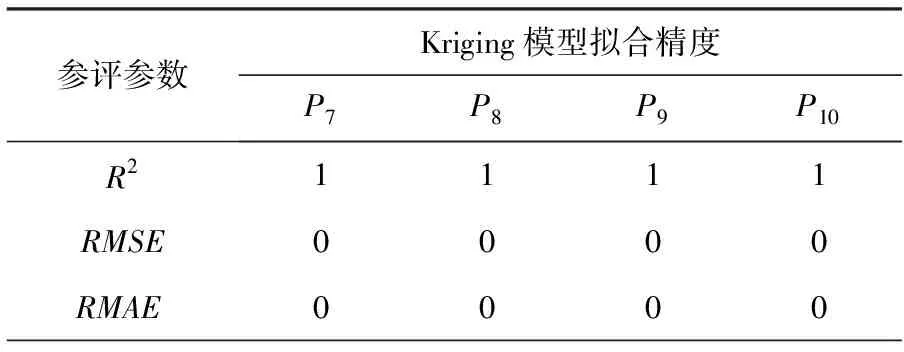
表2 Kriging近似模型拟合精度
3.4.2Kriging近似模型优化效果验证
在Python软件Optimization模块中求解式(2),可获得实验设计的Kriging近似模型优化的Pareto解集分布图,其中一组解集分布如图6所示,图中深色点和浅色点分别表示优化数值低和优化数值高的解集。由图可知,深色点解集的数量明显高于浅色点解集的数量,且分布范围更广,证明通过Kriging近似模型进行焊接机器人龙门架参数优化可取得较好的效果。
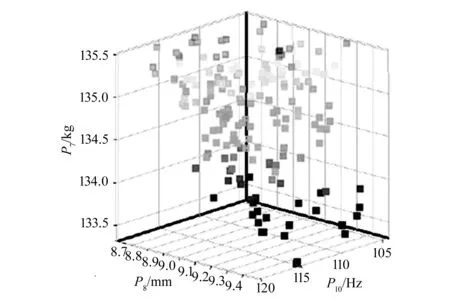
图6 Kriging近似模型优化的Pareto解集分布
为进一步分析Kriging近似模型的优化效果,对比了采用MOGA算法求解所得近似模型和非参数回归(NPR)近似模型对焊接机器人龙门架结构的优化效果,结果如图7所示。由图可知,相较于NPR近似模型,Kriging近似模型优化的焊接机器人龙门架结构,优化后得到的焊接机器人龙门架结构总质量明显更小,因此采用Kriging近似模型优化焊接机器人龙门架结构效果更好。
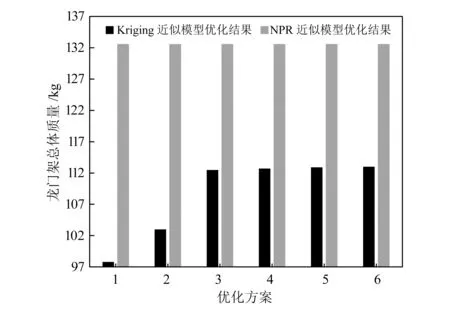
图7 不同近似模型总体质量优化结果
3.4.3优化后焊接机器人龙门架结构特性分析
1)静态特性分析。
为验证Kriging近似模型优化的焊接机器人龙门架结构的合理性,通过实验分析优化后焊接机器人龙门架结构的静态特性。表3为优化前、后焊接机器人龙门架的尺寸、质量和静态特性。由表可知,采用所提方法优化后的焊接机器人龙门架结构静变形量和最大等效应力分别增加了104.22%和102.11%,为0.014 5 mm和2.87 MPa,但仍远小于材料许用值;总体质量减少了45.88%,为111.23 kg。由此说明,采用所提方法对焊接机器人龙门架结构的优化效果明显。
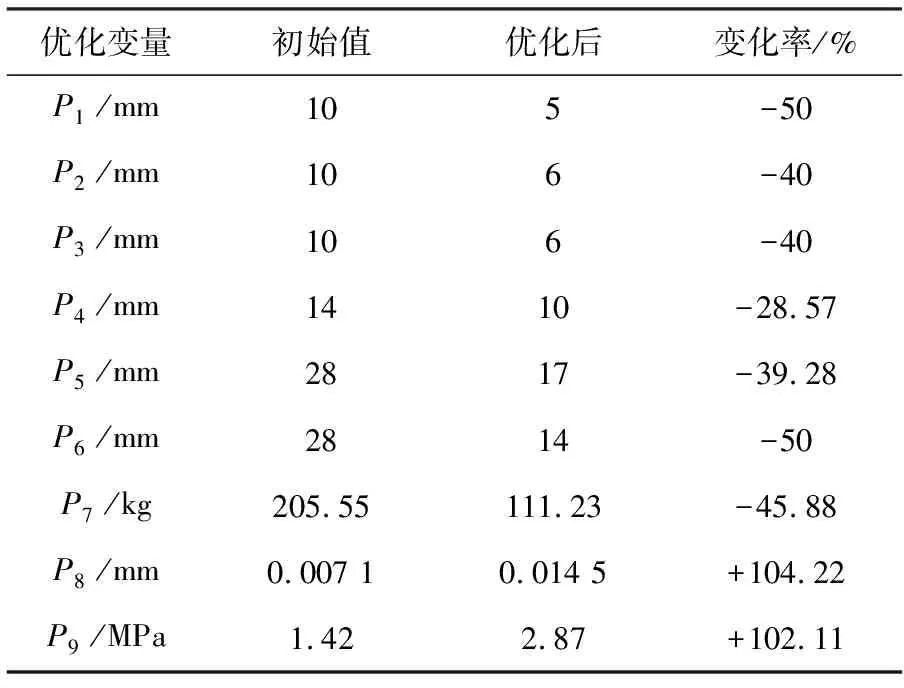
表3 焊接机器人龙门架结构优化前、后静态特性对比
2)动态特性分析。
考虑到焊接机器人运动过程中所受外部激励载荷较小,因此为分析优化后的焊接机器人龙门架动态特性,实验选取焊接机器人龙门架结构前6阶模态进行分析。表4为采用所提方法优化前、后焊接机器人龙门架结构前6阶模态频率对比。由表可知,优化后的焊接机器人龙门架第1、2、3、5阶模态频率比优化前增加,第4、6阶模态频率比优化前降低,但整体变化率较小,小于20%;最大变形量均有所增加,但变化量相对较小。由此说明,采用基于MOGA求解得到的Kriging近似模型优化的焊接机器人龙门架结构具有良好的动态力学性能。
4 结束语
本文所提的基于MOGA算法的焊接机器人龙门架结构优化方法,通过构建焊接机器人龙门架Kriging近似模型,并以焊接机器人龙门架结构质量为优化目标,可在满足焊接机器人龙门架结构静态特性和动态特性的前提下,实现焊接机器人龙门架结构优化,从而减小龙门架结构质量。相较于优化前,采用所提方法优化后的龙门架结构质量减小了45.88%,为111.23 kg,具有良好的优化效果,可实现焊接机器人龙门架结构的轻量化设计。

