基于SWDAE-SVC的矿用齿轮箱自监督故障诊断方法

李 鑫

(中国矿业大学机电工程学院,江苏 徐州 221116)

矿用齿轮箱作为一种高效的动力传递部件,被广泛应用于采煤机、掘进机、提升机等矿用机械设备中。然而,矿用齿轮箱常服役于重载、潮湿、高粉尘、强冲击等极端恶劣的工况下,内部零件容易发生各种故障,轻则导致非计划性停机,降低采矿的生产效率,重则引发重大的安全事故,造成财产损失和人员伤亡[1]。因此,开展矿用齿轮箱故障诊断研究对于保障矿用机械设备的可靠性与安全性具有重要意义[2]。

近年来,随着人工智能、物联网、大数据技术的迅猛发展,基于数据驱动的智能故障诊断方法受到了越来越多研究人员的关注[3-4]。于红梅[5]将深度自编码网络与模糊推理相结合,构建了一种端对端的矿用齿轮箱故障诊断方法。宋立杰等[6]提出了一种基于鲁棒最近邻超圆盘的齿轮箱智能故障诊断方法。Shi等[7]提出了一种双向卷积长短时记忆网络模型,并将其应用于齿轮箱故障诊断。Li等[8]构建了一种基于图稀疏随机向量函数链接网络的齿轮箱故障识别方法。王辉等[9]设计了一种多尺度注意力深度强化学习网络,并将其成功应用于多工况下齿轮箱故障诊断。

然而,上述基于数据驱动的齿轮箱故障诊断方法仍存在以下两个问题:1)采用监督学习的方式进行建模,这就要求训练样本需准确标注。然而,样本标注是一项费时费力的工作,且难免会出现人为误差,造成样本误标注。2)模型的噪声鲁棒性较差。由于矿用齿轮箱工作环境极为恶劣,持续受到复杂噪声干扰,因此会降低模型的诊断效果。针对上述问题,本文提出了一种基于栈式小波降噪自编码器(stacked wavelet denoising auto-encoder,SWDAE)和支持向量聚类(support vector clustering,SVC)的自监督故障诊断方法,并通过实验验证了所提方法的有效性及优越性。

1 栈式小波降噪自编码器

自编码器是一种经典的无监督学习模型,主要由输入层、隐藏层和输出层三部分组成,其中输入层和隐藏层构成编码器,隐藏层和输出层构成解码器。自编码器通过编码和解码运算重构输入数据,并以重构误差作为模型的优化目标,自主挖掘数据中的隐藏特征。

给定输入样本x,x∈Rd,通过非线性映射函数fθ(x)将其编码到m维隐藏层,隐藏层特征h为:

h=fθ(x)=δ1(W1x+b1)

(1)

式中:结构参数θ={W1,b1},W1和b1分别为输入层与隐藏层间的权重矩阵和偏置,δ1(·)为编码器的非线性激活函数。

随后,通过非线性映射函数gκ(h)将隐藏层特征h进行解码重构,获得输出特征y:

y=gκ(h)=δ2(W2h+b2)

(2)

式中:结构参数κ={W2,b2},W2和b2分别为隐藏层与输出层间的权重矩阵和偏置,δ2(·)为解码器的非线性激活函数。

(3)

为了提高自编码器的鲁棒性,Vincent等[10]提出了降噪自编码器(denoising auto-encoder,DAE),通过随机“污染”部分输入数据,并对其进行编码和解码运算以获得“纯净”的重构数据,从而提取更具有鲁棒性的隐藏特征。DAE通常采用Sigmoid、Tanh、Rule等激活函数实现特征的非线性映射,然而上述激活函数对非线性、非平稳及噪声干扰数据的感知能力有限。因此,本文将Morlet小波映射函数引入DAE以构建小波降噪自编码器(wavelet denoising auto-encoder,WDAE)模型。

对于训练样本x,WDAE隐藏层的第j个输出hj可表示为:

(4)

式中:ψ(·)为Morlet小波映射函数,xk为x的第k维,Wjk为第j个输入单元与第k个隐藏单元间的权重系数,aj为激活函数的伸缩参数,cj为激活函数的平移参数。对于实数t,Morlet小波映射函数可具体表述为:

ψ(t)=cos(5t)exp(-t2/2)

(5)

通过改变伸缩参数aj和平移参数cj,小波激活函数可感知不同分辨率下的数据细节,因而对复杂非平稳信号及强噪声干扰信号具有更强的鲁棒性。

如图1所示,可采用与SDAE相同的网络结构,将多个WDAE进行层层堆叠,以进一步构建SWDAE模型,其中前一个WDAE模型的输出作为当前WDAE模型的输入。SWDAE的训练过程分为前向学习和反向微调两个阶段:首先逐层学习每个WDAE模型结构参数,然后采用反向传播算法对整个模型结构进行微调。SWDAE能够以无监督的方式学习矿用齿轮箱监测数据的深层敏感故障特征,并具有优异的噪声鲁棒性能。

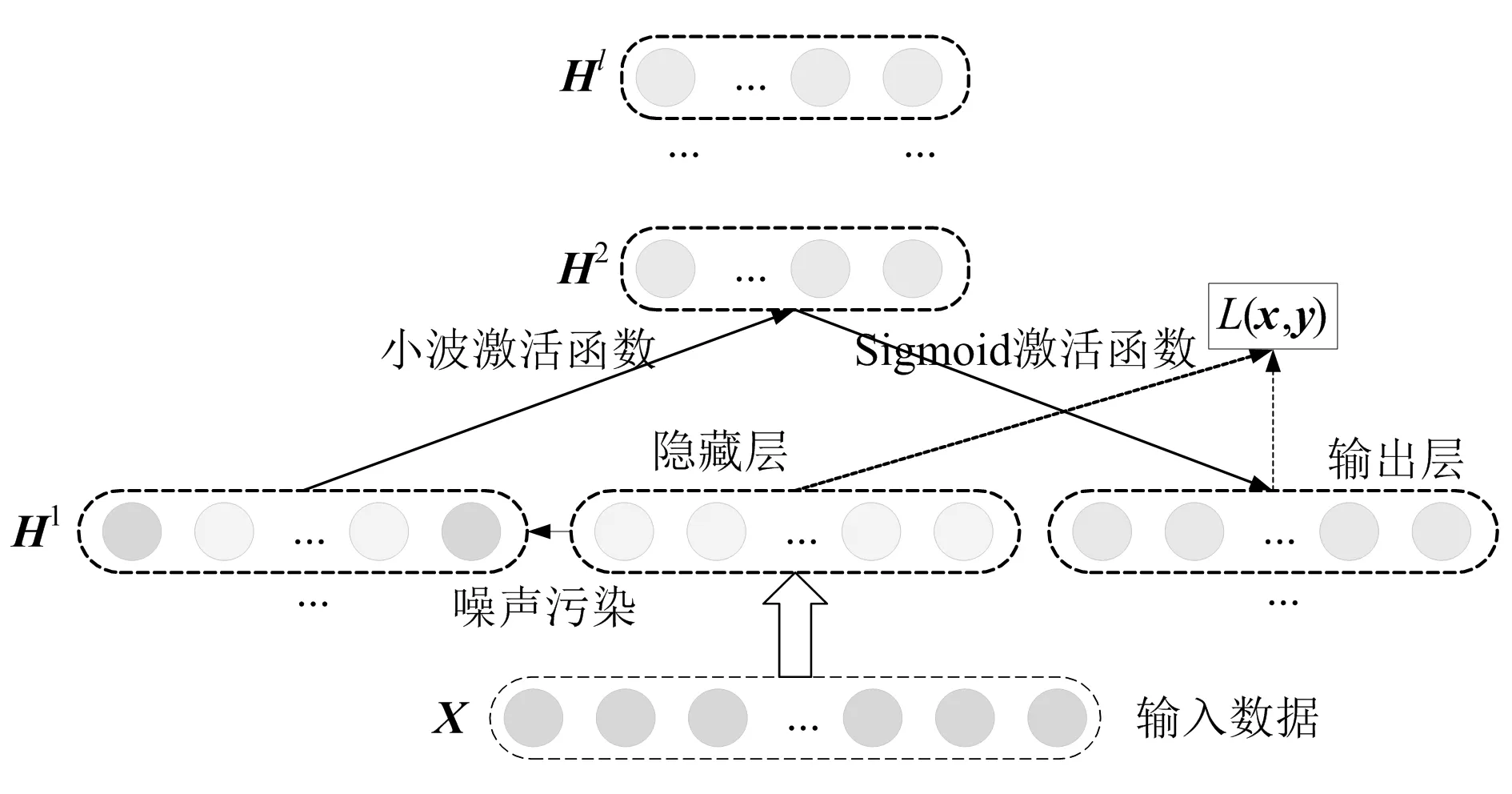
图1 SWDAE的模型结构

2 支持向量聚类模型

(6)

式中:R和o分别为超球体的半径和中心,C为惩罚系数,ζi为松弛因子,φ(·)为核函数,n为训练样本个数。由于高斯核函数具有良好的泛化性和普适性,因而本文选用该核函数以提高模型对非线性数据的处理能力。

可通过Lagrangian乘子法将式(6)改写成下式:

(7)

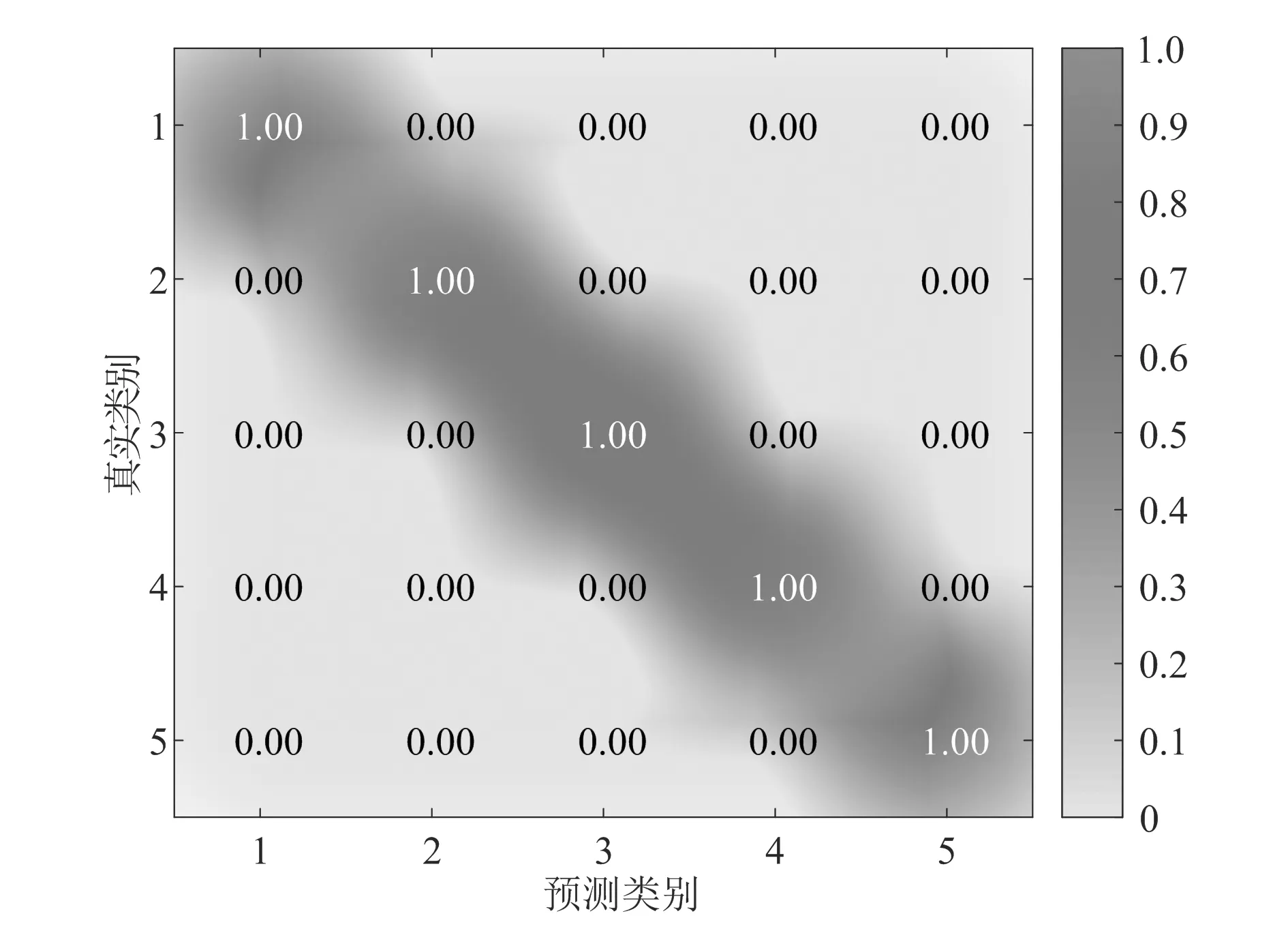
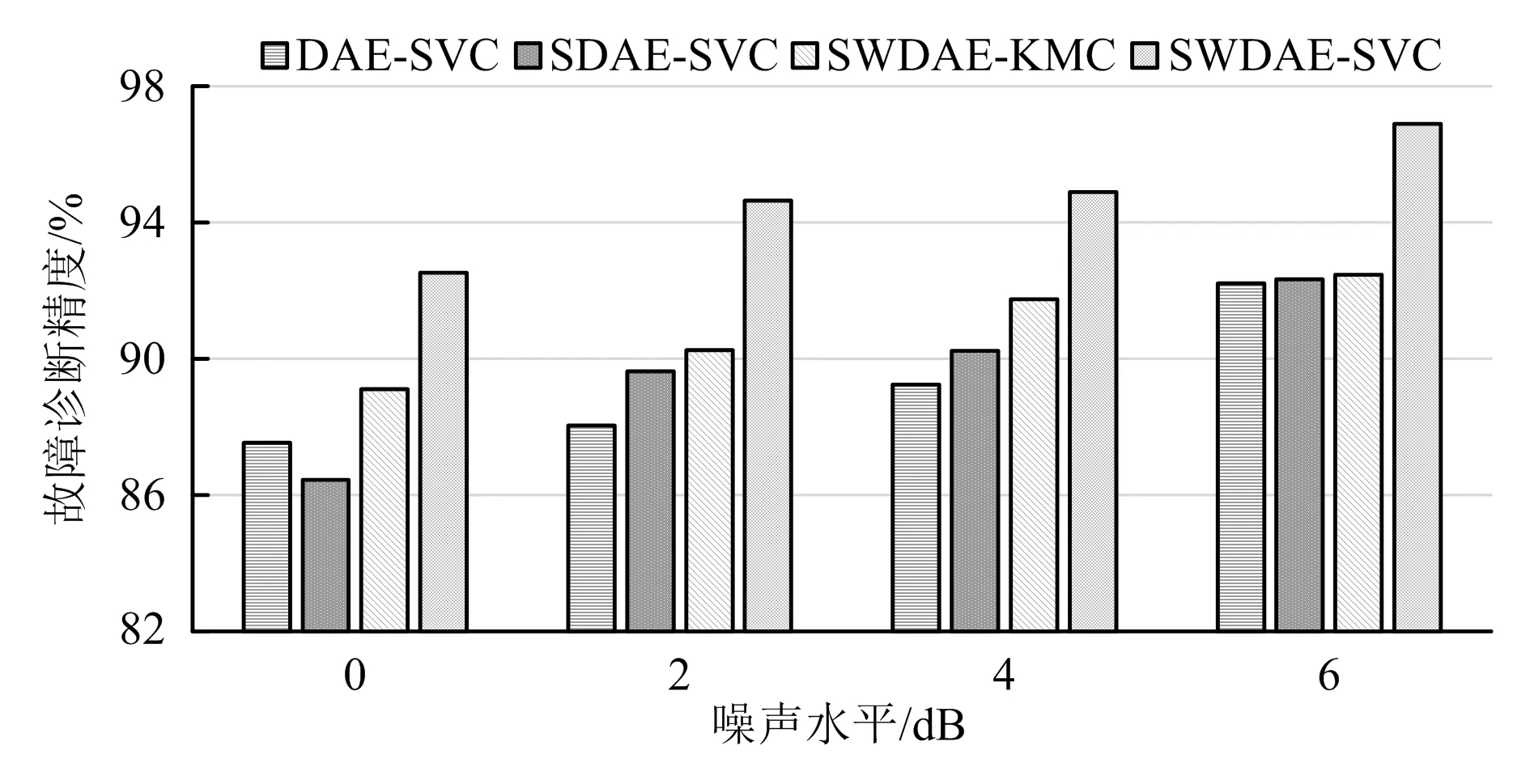
式中:β、βi、βj为Lagrangian乘子。根据KKT条件(Karush-Kuhn-Tucker conditions)可知,当0<βi

3 所提方法的具体流程

综上所述,本文提出了一种基于SWDAE-SVC的矿用齿轮箱自监督故障诊断方法,其中SWDAE用于自主学习振动数据中蕴含的深层故障特征,SVC以无监督学习的方式实现故障类别的精准识别。所提方法的具体流程如下:

1)采集矿用齿轮箱不同运行状态下的振动监测数据。

2)将采集到的振动数据随机划分为训练样本集和测试样本集。

3)采用训练样本集构建SWDAE模型以自主挖掘数据中的深层故障特征,小波映射函数的引入提高了模型的噪声鲁棒性。

4)利用SWDAE学习到的故障特征构建SVC模型,以无监督的方式构建故障特征与故障类别间的映射关系。

5)利用测试样本集验证所提SWDAE-SVC方法的有效性。

4 实验验证与分析

为了验证所提方法的有效性,选用文献[13]所提供的齿轮箱故障公开数据集进行实验分析,具体实验装置如图2所示。在本实验中,总共考虑5种齿轮箱状态,包含正常健康状态、缺齿故障、缺块故障、齿面磨损及齿根裂纹。在信号采集过程中,制动控制器的电压为2 V,输入转速为1 800 r/min。为体现所提SWDAE-SVC方法的有效性,将其与DAE-SVC、SDAE-SVC及SWDAE-KMC(KMC表示K-means聚类模型)方法进行对比分析。

图2 齿轮箱实验台

每种健康状态包含1 000个样本,分别随机挑选100、300、500及600个样本作为训练样本,剩余样本用于模型测试。每种训练样本下各模型重复运行10次,具体诊断结果见表1。从表1中可以看出,所提SWDAE-SVC方法在每种样本情况下都取得了最高的故障诊断精度,表明了该方法的优越性。DAE-SVC在所有模型中的故障诊断表现最差,这说明浅层模型(DAE)的特征学习能力要弱于深度学习模型(SWDAE和SDAE),只能学习到较为简单的故障特征。由于SWDAE采用小波激活函数进行非线性特征映射,对复杂的非平稳信号具有更强的适应性,因而SWDAE-SVC的故障诊断性能要优于SDAE-SVC。此外,对比SDAE-SVC和SWDAE-KMC的故障诊断结果,可发现SVC的无监督故障分类性能要强于KMC。图3为SWDAE-SVC在训练样本为600时的最高故障诊断精度。从图3可知,SWDAE-SVC将所有的样本都准确分类,故障诊断精度高达100%。

表1 不同训练样本下各模型的诊断精度 %

图3 SWDAE-SVC的最高故障诊断精度

此外,在原始数据中加入信噪比(SNR)为0 dB、2 dB、4 dB及6 dB的高斯白噪声,以验证所提方法的噪声鲁棒性。信噪比的计算公式为:

SNR=10lg(Ps/Pn)

(8)

式中:Ps为信号功率,Pn为噪声功率。图4展示了各模型在不同噪声水平下的故障诊断精度。从图4可以看出,所提SDAE-SVC方法在各噪声水平下都取得了最高的故障诊断精度,这说明所提方法具有良好的噪声鲁棒性。在0 dB、2 dB、4 dB及6 dB噪声水平下,SWDAE-SVC方法的故障诊断比SDAE-SVC方法高3.42%、4.40%、3.15%和4.43%,表明小波激活函数能有效提高SWDAE的抗噪声干扰能力。

图4 不同噪声水平下各模型的故障诊断精度

5 结论

本文提出了一种基于SWDAE-SVC的矿用齿轮箱自监督故障诊断方法,旨在解决传统故障诊断方法极度依赖样本标签及噪声鲁棒性差等问题,得到的主要结论如下:

1)SWDAE采用小波激活函数进行非线性映射,极大提高了模型对复杂非平稳信号及噪声污染数据的适用性,能够自主学习蕴藏在振动监测数据中的深层次敏感故障特征。

2)SVC可以在无样本标签下以自监督学习的方式构建故障特征与故障类别间的非线性映射关系,其分类性能要优于常用的KMC方法。

3)所提SWDAE-SVC能够实现矿用齿轮箱故障的精准识别,并具有良好的噪声鲁棒性。