视觉辅助的激光振镜加工畸变校正及精度分析

朱铁爽,张承瑞+

(1. 山东大学 机械工程学院,山东 济南 250061;2.山东大学 高效洁净机械制造教育部重点实验室,山东 济南 250061)

0 引言

激光加工是利用高能激光束聚焦于待加工区域,在工件表面留下印记或使材料熔化、气化而被去除的特种加工技术。激光加工具有能量密度高、热变形区域小、无机械加工应力、加工工具损耗率小、可加工高硬脆材料、加工过程噪声小且不使用切削液、易于集成自动化控制等优势,是一种高效安全、绿色环保的加工方式,广泛应用于航空航天、汽车船舶、数码电子等高端制造领域。激光振镜技术是利用两个相互垂直布置的振镜电机在小范围内快速偏转,带动末端反射镜偏转而改变光路,使激光聚焦点在大范围加工平面内快速定位的技术。振镜惯量小、重复定位精度高,对于提升激光加工的效率和质量效果明显,是近些年激光加工领域的热门研究方向[1-2]。激光振镜加工典型的应用场景有激光摆动焊接[3]、激光快速标刻、激光清洗、激光表面处理等。

在现有振镜控制系统中,为了减小逻辑运算量并提高实时性,一般采用简化的控制策略代替复杂的坐标—转角映射关系,从而产生非线性误差。这种误差在靠近加工平面中心的区域并不明显,但在加工平面边缘区域会显著增大,直接影响激光加工的定位精度和加工质量。赵中民等[4]根据误差来源将振镜系统固有误差归纳为测距误差、角度误差和枕形误差,分别采用多次测量取均值、建立补偿曲面和动态改变扫描范围的方法对应解决各误差,效果明显,然而该方法对3种误差分别进行消除,期流程冗杂,效率较低,不适于工业化应用;郭飞等[5]采用硬件电路校正振镜加工畸变,该系统结构紧凑且实时稳定,然而硬件方案算力低,不利于复杂校正算法的实现,且系统成本高、柔性差。一般的工业应用通过软件算法对振镜加工误差进行后处理补偿,通常采用公式法计算补偿量或建立补偿表进行插补[6-7],图形畸变校正效果明显,满足标刻等一般激光加工要求,然而该类方案的畸变量多采用人工测量或用平移台辅助测量,其精度差、效率低;TU等[8]从振镜模型参数视觉标定的角度出发,对振镜偏转角进行软件估算补偿,将系统定位误差控制在0.5 mm左右,提升了抗噪性,然而该模型精度还需提高;CHEN等[9]、LE等[10]、BESSMELTSEV等[11]学者引入机器视觉方案,通过识别等距网格的角点坐标计算得到畸变量,进一步提升了校正精度,然而角点检测算法对激光质量、标刻工艺、相机静态性能等要求较高,其算法稳定性、鲁棒性较差,适用范围有限。

针对以上问题,本文提出一种优化的视觉辅助的激光振镜加工系统畸变校正方案,可高效、精确、稳定地消除图形轨迹误差。本文通过分析畸变产生的原因建立畸变数学模型,采用“螺旋式填充圆”标刻配合“最小包络圆”视觉检测算法获得特征点坐标,并计算得到平面两个维度的畸变量,然后分别用二次曲线拟合和点阵线性插补算法进行单因素多水平畸变校正实验,对比分析校正效果,得到最优参数。

1 畸变模型的构建

1.1 产生原因

激光振镜加工的畸变来源于系统误差和偶然误差两方面。系统误差包括采用简化的控制策略导致的方法误差、机械机构和光学结构的加工误差与装配误差,以及振镜偏转过程中的定位误差等;偶然误差包括由环境温度的变化、机械振动、供电电源电压波动等因素造成的误差。其中,采用简化控制策略导致的方法误差远大于其他误差,在振镜畸变中占主要部分,其他误差对振镜畸变的影响较小,归为非方法误差。对方法误差分析如下:

激光振镜系统在二维平面内的定位主要由振镜电机驱动的相互垂直布置的X轴反射镜和Y轴反射镜完成。激光光束分别经过具有特定机械偏转角的两轴反射镜后产生两倍的光学偏转角来改变光路,最后由F-theta平场镜聚焦于工作平面特定点,如图1所示。

通过光学几何模型计算得到两轴振镜偏转角和理论位置坐标之间的映射关系[12]:

(1)

(2)

式中:(x,y)为理论位置坐标;(α,β)为X轴和Y轴对应的振镜电机的偏转角度;f为F-theta平场镜的焦距。可见(x,y)和(α,β)之间存在复杂的非线性关系,而且从(α,β)到(x,y)的反映射几乎找不到精确的解析解。因此在实际应用中,式(1)和式(2)通常用如下简化的线性关系代替[13]:

(3)

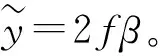
(4)

振镜加工的图形畸变由沿X方向的枕形畸变和沿Y方向的桶形畸变叠加而成,距离平面中心越远,误差越大,如图2所示。

1.2 畸变模型

设X方向和Y方向的方法误差分别为Δx和Δy,

(5)

(6)

设X方向和Y方向的非方法误差分别为δx和δy,且δx远小于Δx,δy远小于Δy,则总误差Dx和Dy分别为:

Dx=Δx+δx;

(7)

Dy=Δy+δy。

(8)

综合式(1)～式(8),得到描述振镜加工图形畸变的数学模型表达式:

(9)

2 校正算法设计与优化

2.1 校正补偿算法

激光振镜加工的轨迹图形畸变校正采用离线处理和在线补偿方式。校正流程如图4所示,主要分为4个步骤:①加工标定图案;②测量获得特征点坐标;③形成误差特征描述或校正参数描述;④执行软件控制内核补偿算法。校正补偿算法有曲线拟合补偿和线性插补补偿,下面设计这两种算法并用畸变数学模型进行仿真校正。

曲线拟合法是公式驱动的补偿方法,其所需标定点数少,操作效率高但补偿精度低。该算法需要获得加工平面内9个特征点的位置坐标,如图5a所示,然后以中心点和4个坐标轴线点为基准,计算出4个象限特征点的坐标误差,并由经验拟合公式(10)和(11)计算出两个分量4个象限的8个补偿系数k1～k4和k′1～k′4,根据目标点所在象限调用相应补偿公式对点坐标进行校正。结合畸变理论模型(9)对高次曲线拟合补偿算法进行仿真,仿真结果如图5b所示,可见在标定特征点附近畸变校正效果较好,在远离标定特征点区域则校正效果有限。

(10)

(11)

线性插补法是数据驱动的补偿方法,其采用n×n个标定点(n=3,5,7,…),n的取值越大校正精度越高,校正所需的操作时间越长。以n=5为例,如图6a所示,在加工平面范围内等距定位25个特征点坐标,通过与坐标轴上的对应投射点做差计算出各个特征点的坐标误差,分别建立X方向和Y方向的误差表,判断目标点所在网格位置(如图7),根据网格插值公式(12)和(13)[7]计算得到目标点的坐标误差,并补偿到振镜命令位置坐标,从而完成校正。结合畸变理论模型(9),对n=5时的线性插补拟合补偿算法进行仿真,仿真结果如图6b所示,可见畸变基本消除,且效果优于曲线拟合法。

(12)

(13)

2.2 特征点识别算法优化

对于激光振镜标刻后的特征点坐标,通常采用人工测量或配合两轴移动台目测定位的方式获得,精度和效率较低;本文采用机器视觉识别的方式代替人工测量,在解决精度问题的同时可以大幅提高校正效率。校正过程中的识别问题不是单一的视觉识别问题,它还包括标刻图案设计、标刻材料选择、激光标刻工艺、相机设备选型、图像预处理等贯穿整个流程的其他问题,最终目标是在保证校正精度和效率的同时,提高系统的稳定性和鲁棒性。

对于标定图案的设计和特征点识别,本文拟定3种方案:①非填充圆阵列+霍夫圆变换[14-16],如图8a所示;②等距网格+亚像素角点检测[9-11],如图8b所示;③螺旋式填充圆阵列+最小包络圆检测,如图8c所示。方案①和方案②采用单线条标刻,由于振镜存在加减速过程,在激光加工起始和终止时刻易造成过烧和烧穿现象,使特征信息丢失,影响视觉识别,如图8d和图8e所示。方案①在畸变较大处标刻的理想圆实际呈椭圆状,霍夫变换算法会识别出多个干扰圆,无法确定实际圆心,如图8f所示。在方案②中,直线标刻过程中激光功率和轨迹波动会干扰角点检测算法,从而产生误判,如图8g所示。方案③采用螺旋式填充圆标刻,螺旋线轨迹设计如图9所示,轨迹间距设置等于线条宽度,以填满圆形区域,螺旋线填充与传统平行线填充相比,轨迹和速度连贯无突变,由加减速造成的缺陷在整个加工图形中占比很小(如图8h),在圆心处可能存在过烧,然而因为包络圆算法考虑连通区域的外部边界,所以圆心处的缺陷不影响视觉识别。综上所述,方案③的算法识别稳定性和抗干扰能力最优。

本文选用激光标定黑底相纸作为基底材料,用激光标刻的方式在其表面加工出标定图案,最后选用已经过标定和校正的高分辨率单色相机正对拍摄取图。本文实验均以振镜内部单位作为长度度量,根据振镜控制协议XY2-100[17],单个振镜的位置精度为16位,范围为-32 768～+32 767。标定特征检测算法流程如图10所示,主要步骤包括:①输入参数和图像;②图像预处理;③查找最小包络圆;④剪枝优化集合;⑤重复执行以上步骤,直到集合大小等于特征点数n×n;⑥点排序;⑦求单应矩阵[10]并进行透视变换;⑧构建误差表并应用补偿算法。

3 校正实验

3.1 实验平台

本文校正实验所用的振镜加工头为PSH14二维扫描头,激光源选用IPG 100W脉冲光纤激光器,参数如表1所示;振镜头支撑采用大理石三轴移动平台,可在XYZ3个方向调整振镜位置,整体结构如图11所示;视觉相机选用迈德威视MV-GE500M-T型号的CMOS相机,有效像素为500万,图像分辨率为2 592×1 944,无辅助光源,如图12所示;控制器为自研系统,其基于工业个人计算机(Industrial Personal Computer,IPC)和Windows操作系统开发,可以并行处理实时任务和非实时任务[18]。

表1 振镜头和激光器参数

续表1

3.2 实验步骤

本文实验变量为畸变校正补偿方法(参数),实验过程中控制其他实验变量不变,横向对比不同方法(参数)的校正精度,以分析校正效果并得出最优参数。实验变量分别取以下值:曲线拟合、3×3线性插补、5×5线性插补、7×7线性插补、9×9线性插补、11×11线性插补。实验步骤如下:

(1)标定特征图案设计 设计了5种圆阵列图案如图13b所示,分别进行离线仿真加工预览。

(2)标定特征图案加工 在相纸上实际加工设计的标定图案,加工工艺为线速度105unit/s、加速度107unit/s、激光功率10%、脉冲频率100 kHz、跳转延时50 ms(适配RS232通信速率)。加工结果如图13a所示。

(3)特征点识别与误差计算 通过机器视觉的方法自动识别和定位各特征点,计算理论点和实际点位置差异,如图13c所示,并构建误差表。该振镜桶形误差远大于枕形误差,桶形误差分布如图13d所示,与1.2节建立的模型一致。

(4)误差补偿及效果验证 依据误差表对振镜指令位置进行补偿校正,校正后加工图案的畸变与未校正相比明显减小,如图14a所示(以11×11标准点阵为例)。

3.3 校正效果与精度分析

建立校正效果评价机制,采用误差测量标准点阵对校正后的振镜系统进行标定,获得11×11标定点精度。图14所示分别为未校正和6次校正实验后的标准测量点阵,以及X向和Y方向校正后的误差分布,分析可得以下规律:

(1)方法误差与非方法误差同时存在且相互叠加,其中方法误差占主导。

(2)方法误差为非线性分布,在远离中心点的方向上误差逐渐增加且增加趋势逐渐变大。

(3)校正前误差越大,校正误差消除率越高,校正效果越明显。

每组实验重复5次取平均值,对X方向和Y方向误差作矢量和,以校正前后最大误差和平均误差为评价变量做误差统计图,如图15所示。最大误差由校正前的1 411.12下降到校正后的最小193.58,平均误差由校正前的259.03下降到校正后的最小36.49,误差去除率为86%。本实验校正范围为50 000×50 000,因此校正后的平均相对精度最优达到7×10-4。分析补偿算法(参数)对校正效果的影响,可得以下规律:

(1)最大误差与平均误差的变化趋势大致相同。

(2)校正特征点数n×n设置得越多,校正后的误差越小。

(3)n>5时增加校正特征点数对校正精度的提高效果有限。

4 结束语

本文以激光振镜加工系统为研究对象,提出一种视觉辅助的畸变校正和精度分析方法。通过分析振镜加工的误差来源,建立了畸变数学模型,并仿真验证了消除曲线拟合算法和线性插补算法误差的效果;提出一种机器视觉代替人工测量获取振镜系统误差特征描述的方法,以螺旋式填充圆标刻配合最小包络圆检测提取标定特征点坐标信息;为检测校正后的振镜加工精度,建立了误差标准测量点阵,以获得X和Y两个方向在加工幅面范围内的误差分布。

实验验证表明,本文方法可以去除86%的图形畸变,校正后的平均相对精度可达7×10-4,校正效果明显;同时,缩短了测量时间,提高了畸变校正的效率、稳定性和鲁棒性。今后将以此为基础优化和完善激光振镜加工校正和控制系统。