新型负泊松比梯度结构缓冲性能

朱冬梅 ，鲁光阳，杜瑶，赵诚

（北京科技大学 机械工程学院，北京 100083）

负泊松比结构会在受到冲击载荷时向受冲击部位附近收缩，使受冲击部分结构密度增大，这与传统的正泊松比蜂窝结构的表现不同.因此，负泊松比结构能在变形过程中吸收更多冲击产生的能量，从而更加有效地抵抗冲击载荷的影响，现阶段关于负泊松比蜂窝结构的研究较多，一些学者们通过改变胞元结构形成新型负泊松比结构，如以最初的内凹六边形结构为基础提出了手性、星形、菱形、方形网格、折叠V 字结构、正弦结构、混合蜂窝结构等负泊松比结构.另有部分学者通过改进传统内凹六边形结构形成新型结构，如马瑞君等［1］基于已有的内凹六边形蜂窝和Miura折纸单元，提出了一种改进型内凹六边形蜂窝结构；Li 等［2］将正弦形肋与负泊松比内凹六边形蜂窝结构相结合，采用有限元方法研究结构的能量吸收能力；Hou等［3］改进了二维多层次内凹蜂窝结构.

在对负泊松比结构缓冲性能的研究中，学者们主要是通过分析改进负泊松比结构在受到冲击载荷时的变形模式和能量吸收能力两方面去研究，如张新春等［4］通过有限元模拟内凹六边形蜂窝结构的面内冲击行为，分析了内凹角度对结构冲击变形和能量吸收能力的影响.Liu 等［5］用Abaqus/Explicit 模拟了内凹蜂窝结构的平面内动态破碎过程，研究了内凹蜂窝结构的冲击动态响应和吸能性能，并与传统正六边形蜂窝结构的动态冲击响应和吸能进行对比.卢子兴等［6］通过ANSYS/LS-DYNA 软件做了一些关于内凹六边形蜂窝结构的数值仿真模拟，研究了负泊松比蜂窝在不同冲击速度下的变形模式和能量吸收等动力学响应特性.数值模拟结果表明，在动态冲击下，负泊松比行为的产生机制与静态加载下一致.

梯度结构是梯度改变结构的某一参数，从而使结构的性能发生改变的一类新型结构.与均匀的结构相比，具有梯度变化的结构能够在降低初始力峰值、增强抗冲击性能和能量吸收能力等方面发挥较大的优势.梯度结构引起了越来越多的国内外专家和学者们的注意，Xiao 等［7-8］和任毅如等［9］基于不同的厚度提出了梯度蜂窝结构，通过在准静态速度下压溃蜂窝结构，研究了梯度金属塑性蜂窝材料的平台应力和吸能能力，结果表明在准静态速度下的压溃实验预期结果符合参考结果，梯度蜂窝结构能够有效地提升结构的抗冲击能力.刘颖等［10-11］、张新春等［12］基于功能梯度理论，根据胞元几何尺寸调节密度分布，改善结构的吸能能力.吴鹤翔等［13］在密度排布一致的基础上，研究了梯度大小对结构抗冲击性能的影响.Ajdari 等［14］采用有限元方法研究了规则、不规则和密度梯度结构在动态载荷和准静态压缩作用下的力学性能、变形模式以及蜂窝结构整体的能量吸收和抗冲击性能.Yu 等［15］通过变化胞元壁厚以及单胞尺寸来研究四边形梯度结构的力学性能，结果表明在准静态载荷作用下，梯度结构的抗压以及抗冲击性能均比均匀蜂窝结构更优.张新春等［16］通过改变不同填充段胞元微结构，提出了一种多段填充复合蜂窝结构模型，采用有限元方法研究了不同恒定冲击速度下各段结构排布和相对密度对复合蜂窝材料宏观变形模式、动态平台应力、冲击载荷一致性和能量吸收效率的影响.Li 等［17］通过有限元模拟和实验的方法研究了沿横向呈逐层梯度变化的多层蜂窝结构的抗冲击性能.Zhang 等［18］利用有限元分析研究了不同冲击速度下壁厚密度梯度的六边形蜂窝的面内冲击变形和能量吸收.

本文提出一种新型负泊松比结构，利用有限元计算结合实验的方法来探究不同的结构参数梯度排列方式对负泊松比结构抗冲击性能的影响.通过改善传统结构的几何构型来提高结构缓冲吸能性能，为后续探索结构缓冲设计提供一些思路.

1 新型负泊松比结构计算模型

1.1 胞元几何模型

本文以独角仙甲虫作为仿生目标，结构受甲虫鞘翅结构启发，覆盖甲虫身体背面的微观结构，是与外界接触的第一道屏障，可以起到抵抗外界冲击，保护甲虫躯体等作用.独角仙前翅内部芯层结构如图1所示，从图中可以看出，芯层结构为蜂窝结构，且胞元之间连接有小柱.

图1 甲虫鞘翅内部微观结构Fig.1 Internal microstructure of beetle coleoptera

结合甲虫鞘翅微观结构和负泊松比结构提出一种新型负泊松比胞元结构，如图2 所示.结构初始参数设置参考文献［19］.主要几何参数包括圆孔孔距L、倾斜角度θ、胞元高度h、圆形角点直径d以及腰杆长度b.新型负泊松比胞元结构初始参数值设定如表1所示.设定胞元结构壁厚为2 mm.

表1 胞元结构参数Tab.1 Structural parameters of the new negative Poisson’s ratio cell

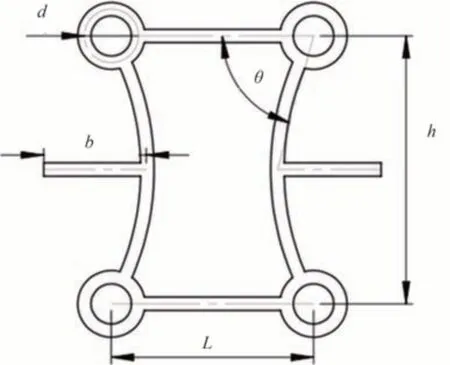
图2 新型负泊松比胞元结构Fig.2 New negative Poisson’s ratio cell structure

1.2 有限元计算模型

建立新型负泊松比结构以及内凹六边形结构的有限元模型并计算比较两种结构的缓冲吸能特性.图3（a）为内凹六边形负泊松比结构（Rchs）有限元模型，图3（b）为新型负泊松比结构（NnPrs）有限元模型.两模型结构的总体高度、宽度、胞元数量、壁厚等均保持一致.

图3 有限元模型Fig 3 Finite element model

模型结构材料选用金属Al，材料力学性能参数如表2所示.

表2 材料力学性能参数Tab.2 Material mechanical property parameters

使用Abaqus 有限元软件进行仿真，结构网格采用C3D8R 实体单元进行划分，同时对冲击过程中的接触均定义为通用接触，设置摩擦系数为0.1.冲击板与结构上表面设置为面与面接触.边界条件的设置为：为防止结构模型在冲击过程中产生倾斜，结构底端完全固定并限制结构模型Z方向的自由度.设置冲击板为刚体，限制其除Y方向位移以外的5个方向的自由度，观察结构在冲击载荷下的变形情况以及缓冲吸能特性.

1.3 缓冲吸能特性评价指标

结构的抗冲击效果可以通过观察结构的初始峰值力来判断，结构在承受冲击载荷发生变形时，初始阶段会产生一个较大的峰值力，从结构抗冲击方面考虑，为了更好地降低对被保护对象的冲击损伤，起到更好的防护作用，要求碰撞初始力峰值尽可能小［20］.结构的吸能效果可以通过比吸能（SEA）进行衡量，它表示单位质量结构所吸收的能量，SEA 越高表明单位质量结构的吸能特性越好，SEA=E/M，其中，M为结构的总质量，E为结构在动态压缩过程中所吸收的总能量，可表示为：

式中：h为结构达到密实化阶段前的有效变形量.

1.4 仿真结果分析

内凹六边形负泊松比结构（Rchs）和新型负泊松比结构（NnPrs）在30 m/s 的冲击速度下的力-位移曲线如图4（a）所示.两种结构的能量吸收情况对比如图4（b）所示.

图4 Rchs和NnPrs结构仿真结果对比Fig.4 Comparison of simulation results between Rchs and NnPrs

可以看出新型负泊松比结构相较于内凹六边形结构的初始峰值力降低了28%，表明新型负泊松比结构有更好的抗冲击性能.观察图4（b）对比曲线，相比而言新型负泊松比结构模型保持良好的能量吸收特性，直到结构变形进入密实化阶段，在压缩后程进入密实化阶段前新型负泊松比结构吸能能力提高35%.

对比两种结构的计算结果，发现新型负泊松比结构在提高抗冲击性能以及能量吸收能力方面都有明显的优势.

2 新型负泊松比梯度结构模型

整体结构为横向排布6个胞元、纵向6个胞元的类蜂窝结构，定义初始非梯度结构模型编号为H，各梯度结构模型编号为C.以胞元角度为梯度变换参数，在保证结构总体高度及除胞元角度外其他参数不发生变化的前提下，将梯度排列方式分为4 种：沿受力方向对称梯度排列，如图5 所示，设计结构参数由上下两端向中间递变，并考虑正梯度以及负梯度的情况，其中正梯度排列指胞元角度两端小的情况，如图5（a）C1 结构所示，负梯度排列指胞元角度两端大的情况，如图5（b）C2 结构所示，沿受力方向分层梯变排列，如图6 所示，通过改变每层胞元的角度来构成，同样考虑正梯度排列方式，如图6（a）C3 结构所示，负梯度排列方式如图6（b）C4结构所示.

图5 对称梯度排列结构Fig.5 Symmetrical gradient arrangement structure

图6 分层递变梯度排列结构Fig.6 Hierarchical gradient arrangement structure

3 缓冲吸能性能对比

C1和C2在30 m/s冲击速度下的变形情况如图7所示.随着冲击刚性板的持续压缩，C1 会在冲击端及固定端同时发生变形，其中冲击端变形较为混乱，固定端会呈现较为规则的“Λ”形，而后结构逐渐压缩进入密实化阶段；C2 则不同，变形会相对集中在冲击端，混乱变形部分和“Λ”形部分的连接相对紧密，固定端变形相对较小，随着冲击的不断持续，变形逐渐向下延伸至发生密实.

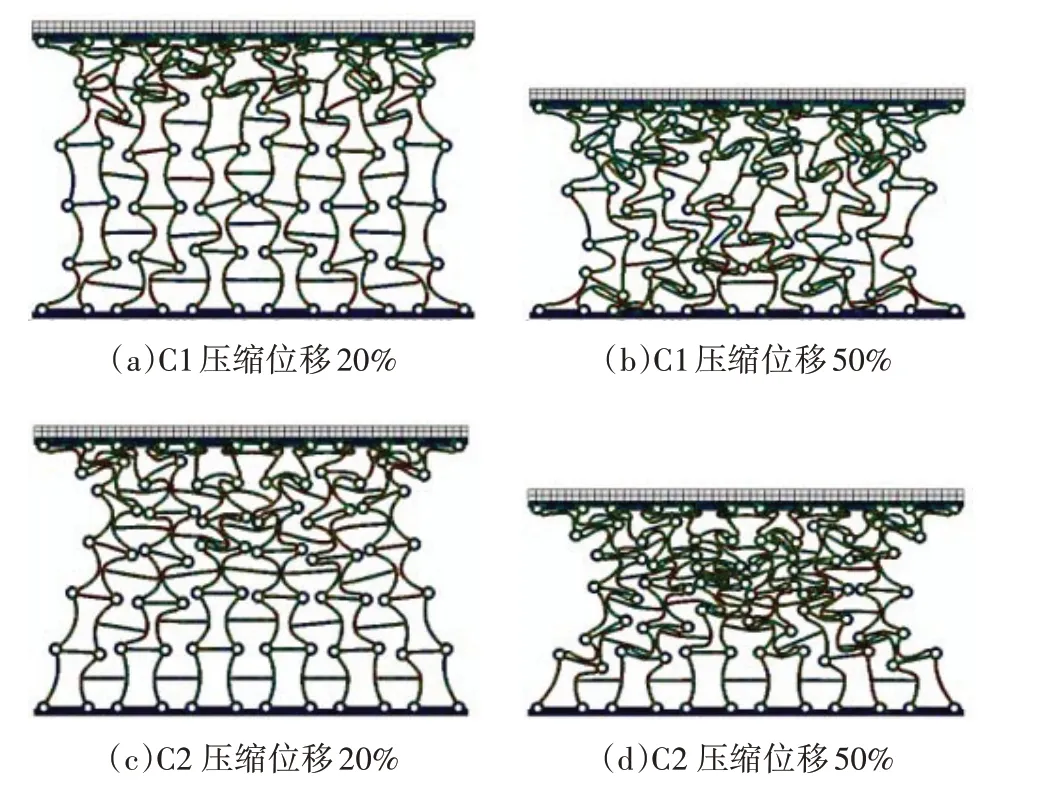
图7 C1、C2结构变形Fig.7 C1 and C2 structure deformation

C1、C2结构性能对比曲线如图8所示，由图8（a）可知，两种梯度变换结构相较于初始结构的抗冲击效果均有一定的改善.从图8（b）比吸能对比曲线中可以看出与均匀结构相比，C1 的能量吸收能力相对较差，C2 的能量吸收能力也与均匀结构的差距不大，由此看出C1、C2 两种梯度变换形式并不能提高结构的能量吸收能力.

图8 C1、C2结构性能对比Fig.8 C1 and C2 structural performance comparison

C3 和C4 在压缩过程中的变形情况如图9 所示.两结构的冲击变形存在较大差别，在冲击初始阶段，C3 的变形集中在冲击端，在结构中间层会产生不明显的“X”形变形，随着冲击过程的持续，这种变形模式由冲击端向固定端拓展；C4 在压缩过程中整体会呈现较为规范的“X”形变形，直到最后发生密实.

图9 C3、C4结构变形Fig.9 C3 and C4 structural deformation

通过观察4 种梯度结构的变形模式可以发现结构在被压缩时，均有明显的收缩现象，因此结构确实有明显的负泊松比效应.

图10 为C3、C4 与均匀结构的力-位移曲线和能量吸收-位移曲线对比图.从图10（a）中可以看出，两种梯度变换结构都可以在一定程度上降低结构在受到冲击时的初始峰值力，C4 的抗冲击效果更好，但C4 在能量吸收能力上的表现相对较差.相比之下，C3 的能量吸收能力更强，这与C3 的变形模式对应.由图9（a）和9（b）可知，C3 压缩变形首先在冲击端发生，然后向固定端扩展，即引入梯度之后会延缓强度较大层的变形，因此尽管在开始压缩的一段范围内梯度模型相对于均匀模型吸收的能量相同，但随着压缩过程的不断进行，C3模型的吸能能力得到了进一步的强化.

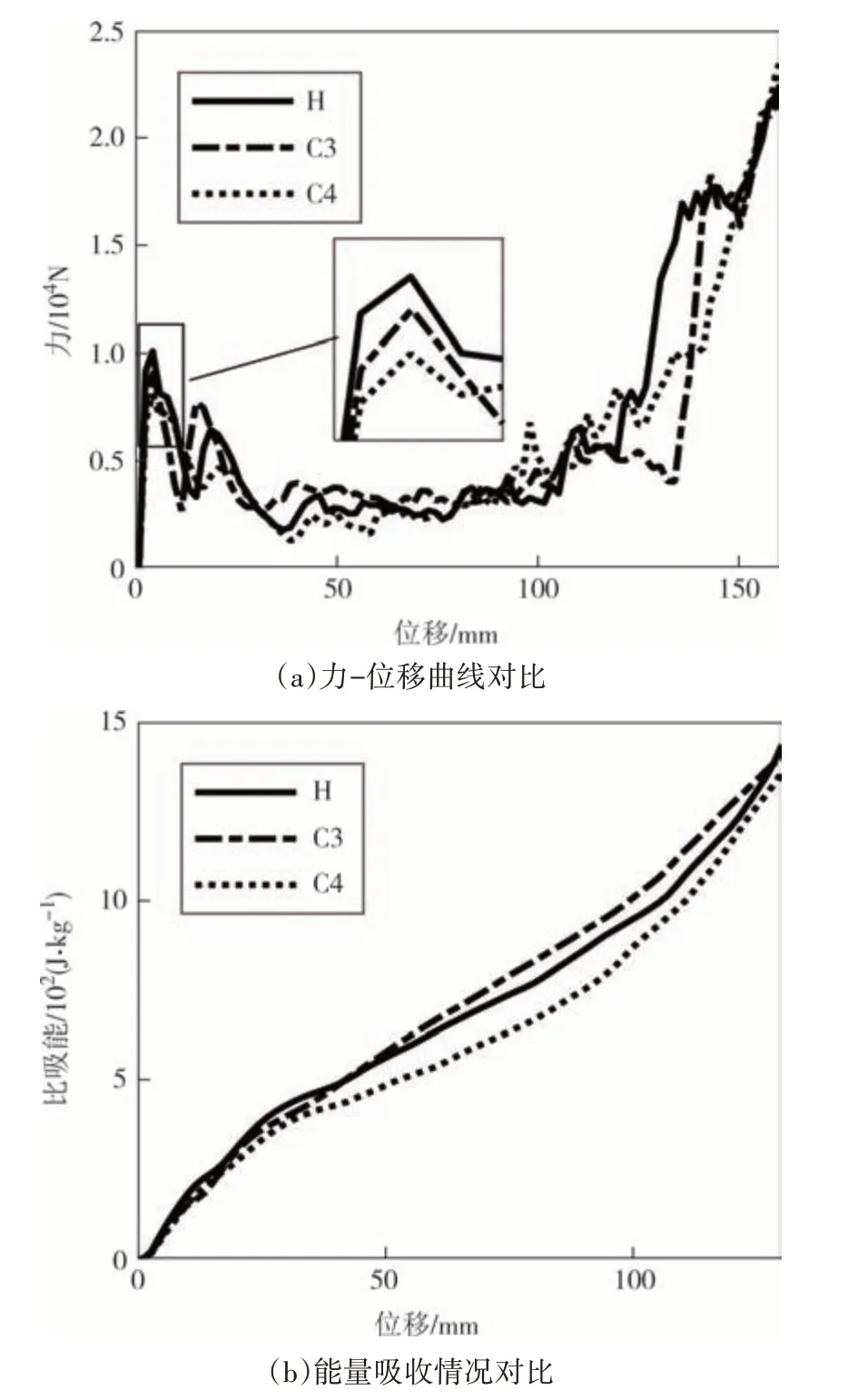
图10 C3、C4结构性能对比Fig.10 C3 and C4 structural performance comparison

综上分析，4种梯度变化方式均可提高结构的抗冲击性能，C3 梯度排列可以强化结构的能量吸收能力.

4 结构缓冲性能实验验证

为了分别对比新型负泊松比结构和梯度结构的抗冲击性能和能量吸收性能，对结构进行压缩实验测试.选用均匀结构和C3 结构进行实验样件3D 打印，考虑实验的成本和加工难度，将原始结构等比例缩小后使用不锈钢基体材料进行打印.

将实验件放在微控电子万能实验机上进行实验，以准静态压缩评价缓冲吸能特性［6］，设定压头速度为60 mm/min；压缩过程持续至结构进入密实化阶段为止，通过计算机输出实验过程的力-位移曲线，并记录结构在压缩过程中的变形情况.

4.1 均匀结构准静态压缩实验

实验件安装状态如图11 所示.压头置于实验件顶端平面，控制压头向下压缩.

图11 实验件安装状态Fig.11 Installation status of test piece

记录实验过程中结构的变形情况，并与仿真模拟的结构变形对比，如图12所示.

图12 均匀结构实验变形模式与仿真对比Fig.12 Experimental and simulation comparison of compression deformation mode of homogeneous structure

可以看出，实验过程中结构变形与仿真模拟的结构变形情况大体一致.主要表现为在整个冲击过程中，结构整体出现明显“/”形变形直至完全压溃.

在采集系统中提取结构的实验数据，并与相同工况下仿真数据对比分析，绘制结构力-位移曲线和比吸能-位移曲线，如图13所示.

图13 均匀结构实验性能与仿真对比Fig.13 Comparison of experimental and simulation results of the homogeneous structure

数据对比显示结构实验与仿真的初始峰值力误差为6.2%；观察结构的能量吸收情况对比图，可以看出，实验与仿真表现的能量吸收能力随压缩位移变化的趋势一致，从而验证仿真模型的正确性.

4.2 C3结构准静态压缩实验

将C3 实验件以同样的方式放置在实验机上，实现实验件的冲击测试，记录结构在冲击过程中的变形模式，并与仿真模型变形对比，如图14所示.

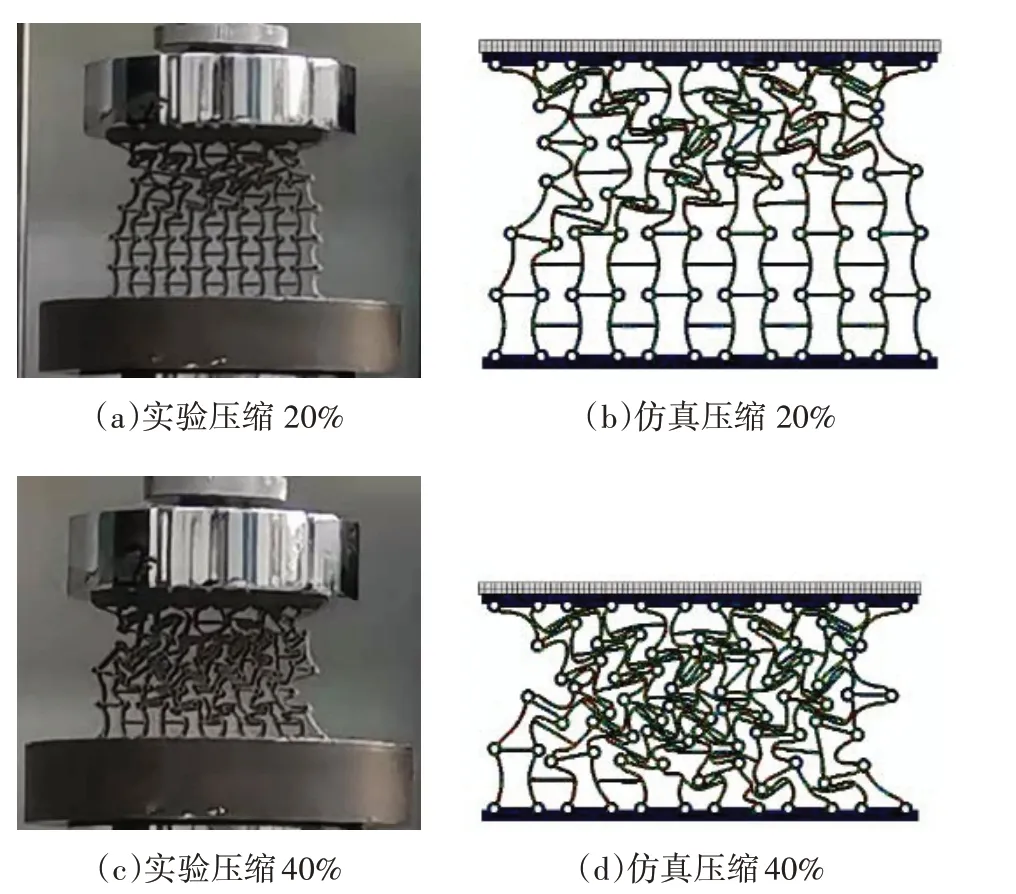
图14 C3结构实验变形模式与仿真对比Fig.14 Experimental and simulation comparison of compression deformation mode of C3 structure

从图14 中可以看出，结构实验的变形情况与仿真过程中的变形情况一致.在初始的较小变形范围内，结构会在靠近冲击端的部分出现一个“V”形的变形带，随着冲击过程的持续，变形由冲击端向固定端拓展，结构内部整体变形更加明显.

同样提取结构的实验数据，并与相同工况下仿真数据对比分析.图15（a）和15（b）为梯度结构实验和仿真计算的力-位移和比吸能-位移曲线对比图，实验与仿真的初始峰值力误差为6.4%；实验与仿真模拟的能量吸收结果表现整体一致，但在结构进入密实化阶段前的差距相对较大，主要是由于在3D 打印金属粉末成型结构材料性能方面存在一定差异.

图15 C3结构实验性能与仿真对比Fig.15 Experimental and simulation comparison of structural performance comparison of C3 Structure

4.3 实验结果分析

对比新型负泊松比均匀结构和梯度结构的实验数据，进行力-位移曲线对比和比吸能-位移曲线对比，如图16所示.

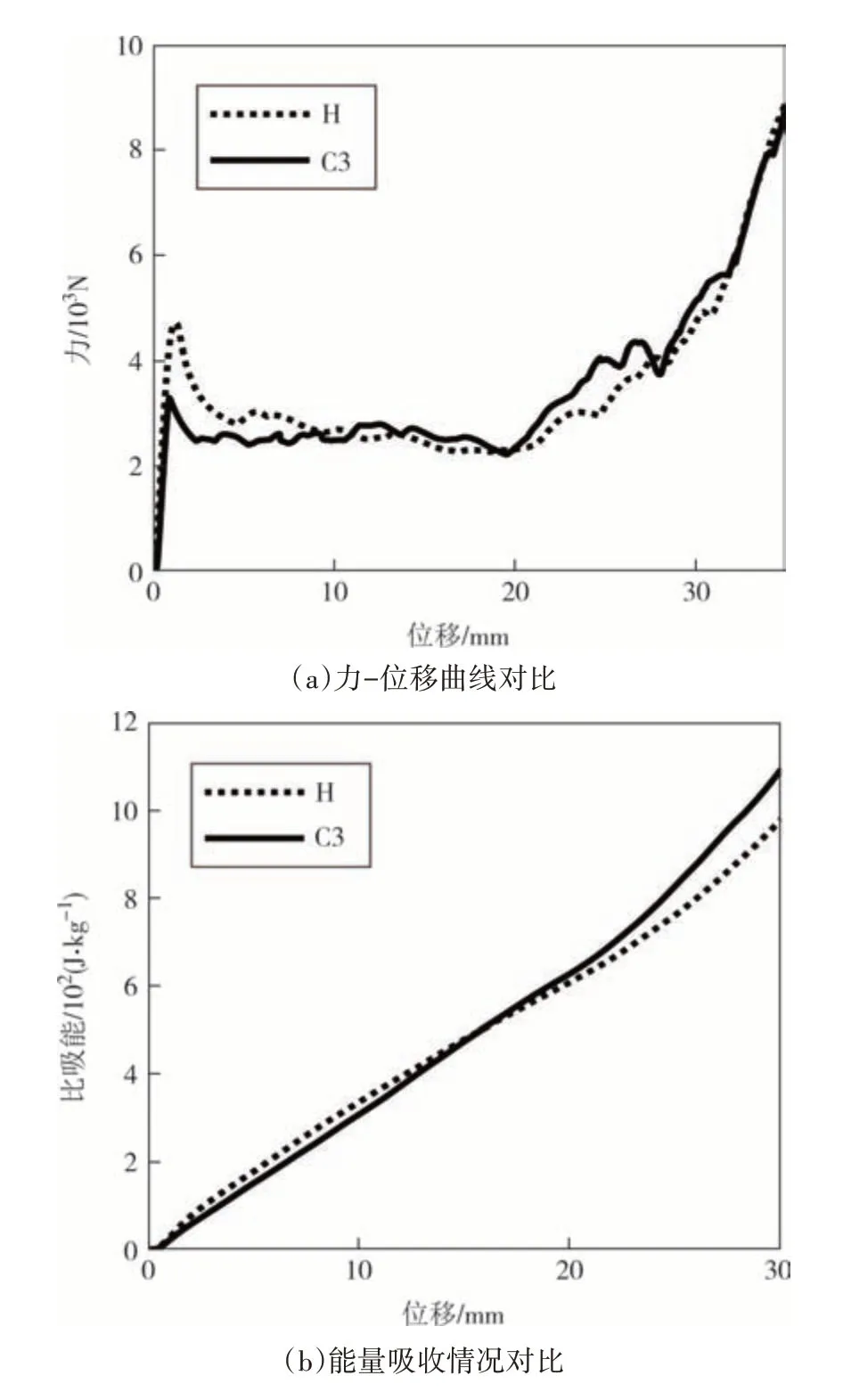
图16 均匀结构与C3结构实验性能对比Fig.16 Comparison of experimental performance between homogeneous structure and C3 structure

由图16 可以看出，梯度结构可以在一定程度上降低冲击时受到的初始峰值力，在结构未进入密实化阶段之前，梯度结构的能量吸收性能会略好于均匀结构，这与仿真对比角度梯度结构（C3）与均匀结构性能时的结论相同.

5 结论

本文主要以构建的新型负泊松比结构为基础，首先与内凹六边形结构对比，研究表明新型负泊松比结构具有良好的缓冲吸能特性；其次对比在冲击载荷下不同梯度排列方式的变化对结构抗冲击性能以及能量吸收特性的影响，阐述了新型负泊松比结构和梯度变换结构的性能差异.主要结论如下：

1）新型负泊松比结构相较于内凹六边形结构在提高结构的抗冲击性能和能量吸收能力方面都有着明显的优势.

2）文中设计的4 种梯度结构在压缩过程中变形模式均有明显不同.C1 结构会在冲击端及固定端同时发生变形，C2 结构的变形则相对集中在冲击端，冲击端混乱部分和“Λ”形部分的连接紧密，固定端变形相对较小；C3 的冲击端变形同样混乱，但在结构中间层会产生不明显的“X”形变形，而C4 在压缩过程中整体会呈现形状较为规范的“X”形变形，直到最后发生密实.

3）4 种梯度排列方式均可强化结构的抗冲击能力，C4 的抗冲击效果最好；但在能量吸收性能方面的表现则各不相同，相较于均匀结构而言，C1 的能量吸收能力相对较差，C2与C4的能量吸收能力也与均匀结构的差距不大，C3的能量吸收能力最强.

4）选用新型负泊松比结构和C3 梯度结构进行准静态冲击实验，并与仿真计算结果比较，对比显示，两结构实验与仿真的初始峰值力误差均在6%左右，能量吸收能力趋于一致.