基于调制比跟踪的三电平变换器VSVPWM 策略研究
李伟 ,王辉 ,刘斯嘉
(1.湖南大学 机械与运载工程学院,湖南 长沙 410082;2.湖南大学 电气与信息工程学院,湖南 长沙 410082)
相对于两电平电压源型变换器,二极管钳位型三电平(Neutral Point Clamped Three-Level,3L-NPC)变换器具有较低的输出电压谐波含量、开关管电压应力与电磁干扰等优点,已经被广泛应用于新能源发电、有源电力滤波器、高压直流输电、电机驱动等中高压、大功率场合[1-2].
交流侧电压的总谐波畸变率(Total Harmonic Distortion,THD)是衡量3L-NPC变换器性能优劣的重要指标,它与调制策略的关系密切[3-6].3L-NPC 变换器调制策略主要有载波调制和空间矢量调制(Space Vector Pulse Width Modulation,SVPWM)两种,国内外众多研究者对这两种调制策略进行了广泛、深入的研究[6-10].文献[7]对载波调制、SVPWM策略之间的关系及其统一理论进行了研究,发现相比于载波调制策略,SVPWM 策略的电压利用率提高了15%.但是,SVPWM策略无法根据调制比的变化实时控制交流侧电压谐波与钳位电容电压.虚拟空间矢量调制(Virtual Space Vector Pulse Width Modulation,VSVPWM)策略是解决这些问题的有效方法[8-9].
有很多文献对VSVPWM 策略进行了深入研究[10-15].文献[10-11]通过构建包含优化因子的最近三虚拟空间矢量模型合成参考电压矢量,并根据中点电压实时反馈较好地实现了钳位电容电压平衡与交流侧电压谐波控制,但是方法复杂,计算量大.文献[12]通过重新定义虚拟矢量,能够使共模电压减小一半,但是所提VSVPWM 策略的电压谐波控制能力弱.文献[13]对增大开关损耗、交流侧电压谐波畸变率的窄脉冲进行了研究,并通过对开关矢量作用时序进行优化调整,在不影响空间矢量合成的前提下避免了绝大部分的窄脉冲.文献[14-15]对采用VSVPWM 策略的3L-NPC 变换器钳位电容电压、线电压谐波等进行了优化,但是都没有考虑虚拟矢量幅值、调制比与线电压谐波之间的关系.总之,传统VSVPWM 策略中,由于参考矢量经过的小三角形区域太多导致该策略在减小开关损耗、抑制交流侧电压畸变率方面存在较大的局限性.
针对采用VSVPWM 策略的3L-NPC 变换器交流侧电压谐波抑制难题,本文设计了一种基于调制比跟踪的高效VSVPWM 策略.首先分析了传统VSVPWM 策略中小三角形区域划分方法的不足;然后详细设计了基于调制比跟踪的VSVPWM 策略,分析了该策略抑制交流侧线电压谐波的机理及该策略与传统VSVPWM 策略之间的关系.所设计的改进VSVPWM策略简单、有效,且在虚拟中矢量幅值与传统中矢量幅值的比值等于调制比时线电压总谐波畸变率取得的最小值.最后,在基于Matlab/Simulink 的仿真实验平台上对本文所设计的VSVPWM 策略进行了验证.
1 3L-NPC拓扑与传统SVPWM 策略
1.1 3L-NPC变换器拓扑结构
典型3L-NPC 变换器的拓扑结构如图1 所示.该变换器由三个单相二极管钳位型三电平变换器桥臂(a、b、c)并联组成,S1a~S4a、S1b~S4b、S1c~S4c为全控型开关,D1~D6为钳位二极管;交流侧连接三相对称交流,R、L分别为电阻、电感;直流端由两个钳位电容C1、C2串联组成.

图1 3L-NPC变换器拓扑结构Fig.1 Topology of 3L-NPC converters
1.2 传统SVPWM 策略
定义每相的开关函数Si(i=a、b、c),P、O、N 为开关函数状态,当Si=P时,S1i、S2i开通,S3i、S4i关段;当Si=O时,S2i、S3i开通,S1i、S4i关段;当Si=N时,S3i、S4i开通,S1i、S2i关段,Si的表达式如式(1)所示.
显然,每相的Si有三种取值,表示每相桥臂具有三种开关状态,因此,三相桥臂具有27 种开关状态,分别对应27 种基本电压矢量,包括3 个零矢量、6 个负小矢量、6 个正小矢量、6 个中矢量、6 个大矢量,如表1 所示.SVPWM 策略的空间矢量图与这27 个电压矢量在该矢量图中的关系如图2所示.

表1 SVPWM 的基本电压矢量Tab.1 Basic voltage vectors of SVPWM

图2 3L-NPC空间电压矢量及其电压矢量图Fig.2 Voltage vectors and voltage vector diagram of SVPWM strategy in 3L-NPC converter
定义调制比m为:
式中:Uref为交流侧a、b、c三相相电压幅值;Uα为三相交流电压转换为αβ两相后在α轴的电压分.
在SVPWM 策略的电压矢量图中,一般将基本电压矢量图分成6个扇区,每个扇区分成6个小三角形区域,如图2 所示[6-7].这种方法虽然简单,但是无法灵活地选择基本矢量,无法灵活地控制钳位电容电压与三相交流侧电压谐波.因此,一些能够灵活地调节交流侧电压谐波、并能更好地控制钳位中点电压的算法得到了广泛关注,如VSVPWM策略[8-9].
1.3 传统VSVPWM 策略
VSVPWM 策略的基本思想是用小矢量和中矢量合成虚拟矢量,并构造新的虚拟空间矢量图;然后在新构造的虚拟空间矢量图中确定合成参考矢量的基本虚拟矢量,并计算各基本虚拟矢量的作用时间;最后确定各基本矢量的作用时间与作用顺序.
VSVPWM 策略中大扇区的划分方法与传统SVPWM 策略相同;小三角形区域的划分方法与传统SVPWM 策略不同,如图3 所示.VSVPWM 中每个扇区被分成5个小三角形区域.

图3 3L-NPC中传统VSVPWM的空间矢量图Fig.3 Voltage vector diagram of conventional VSVPWM strategy in 3L-NPC converter
传统VSVPWM 策略中,大矢量不变,A扇区的虚拟小矢量和虚拟中矢量的表达式为:
式中:V1p、V2p为正小矢量;V1n、V2n为负小矢量;V7为中矢量;VV1、VV2为虚拟小矢量;VV7为虚拟中矢量.
由图3(b)与式(2)可知,基本虚拟矢量能够增加各小三角形区域中合成参考电压矢量的基本电压矢量数,从而增加钳位电容电压控制能力.
在传统VSVPWM 策略中,虚拟中矢量幅值与调制比之间的关系影响参考矢量经过的小三角形区域,进而影响基本矢量的选择,如图4 所示.当0.5 <时,小三角形分布如图4(a)所示,V经过扇区A 的路径为A1→A2→A1.当<m< 2/3 时,小三角形分布如图4(b)所示,V经过扇区A 的路径为A3→A2→A4.当m=2/3时,小三角形分布如图4(c)所示,V经过扇区A 的路径为A3→A4.同理,当m> 2/3时,V经过扇区A 的路径为A3→A5→A4.显然,当m=2/3时,V经过的小三角形区域最少,因此基本电压矢量变化次数最少,电压波形的畸变率最小.但是,当m≠ 2/3时,无法得到最小的交流侧电压谐波,即传统VSVPWM 策略无法随着调制比的变化优化交流侧电压谐波.

图4 传统VSVPWM策略中不同m时A扇区小三角形的划分方法Fig.4 Division method of triangular regions of sector A with different m in conventional VSVPWM strategy
2 基于调制比跟踪的VSVPWM 策略
针对传统VSVPWM 策略的问题,本文提出了一种基于调制比跟踪的VSVPWM 策略,该策略能够显著减小交流侧电压谐波.在该策略中,6 个大扇区的划分方法与SVPWM 和传统VSVPWM 策略一致.大扇区中小三角形区域的划分方法如图5(a)、5(b)、5(c)所示,当时,V落在小三角形区域A1,如图5(a)所示,此时q不随m的变化而变化;当时,V落在小三角形区域A2~A5,当q取两种不同值q1、q2时,得到如图5(b)、5(c)所示的A 扇区小三角形划分.在所提出的VSVPWM 策略中,图6 为V在A 扇区的运动情况,由图6 可知,当m=q时,V经过扇区A的路径为A3→A4,显然此时V在A 扇区经过的小三角形区域最少,电压谐波最小.

图5 基于调制比跟踪的VSVPWM策略中A扇区小三角形划分方法Fig.5 Division method of triangular regions of sector A in proposed VSVPWM strategy

图6 A扇区中m、q之间的关系Fig.6 Relationship between m and q in sector A
在基于调制比跟踪的VSVPWM 策略中,虚拟大矢量不变;虚拟小矢量由正、负小矢量合成;虚拟中矢量由正、负小矢量和中矢量合成.虚拟小矢量和虚拟中矢量的表达式如式(3)所示.
式中:p为正小矢量在虚拟小矢量中的比重;r为正、负小矢量合成的矢量在虚拟中矢量中的比重;s为中矢量在虚拟中矢量中的比重,q=r+s.
由式(3)可知,正、负小矢量幅值大小可变,虚拟中矢量幅值大小可变,中矢量在虚拟中矢量中的比重可变.
此外,在所提出的VSVPWM 策略中,A扇区不同小三角形区域的基本电压矢量如表2 所示,依此类推,可以得到其他扇区对应的基本电压矢量.

表2 A扇区不同三角形区域的基本电压矢量Tab.2 Basic voltage vectors of Sector A
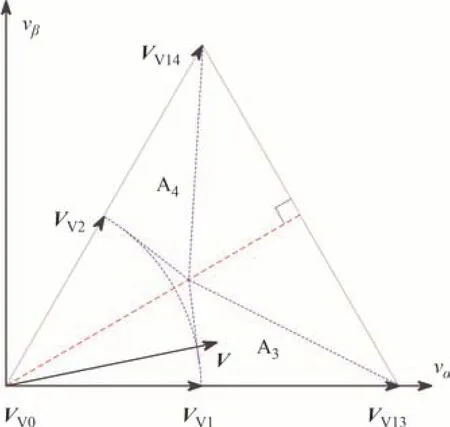
图7 计算小三角形位置的A扇区Fig.7 Sector A to calculate small triangle regions
采用与式(4)类似的方法可以得到A4小三角形区域的位置计算公式如表3所示.

表3 A扇区各小三角形区域位置的判断方法Tab.3 Method to decide triangle regions of sector A
本文所提出的VSVPWM 策略采用最近三矢量法合成参考电压矢量,然后根据伏秒平衡原理计算各基本电压矢量的作用时间.例如,图8 中,当参考矢量V落在小三角形区域A3时,令VV1、VV7、VV13作用一段时间产生的矢量在αβ坐标轴上的投影与V在αβ坐标轴上的投影分别相等,即可得到式(5).

图8 计算参考矢量作用时间的A扇区Fig.8 Sector A to calculate vector action time
式中:T1为电压矢量VV1的作用时间;T7为电压矢量VV7的作用时间;T13为电压矢量VV13的作用时间;Ts是开关周期.由式(5)得到T1、T7、T13分别与Ts的比值的计算公式如式(6)所示.
同理,当参考电压矢量V落在A 扇区其他小三角形区域时,采用相同的方法可以得到各基本矢量的作用时间与开关周期的比值如表4所示.

表4 A扇区各小三角形区域中三个基本电压矢量的作用时间Tab.4 Vector action time of each small triangle region of sector A
本文采用九段法确定基于调制比跟踪的VSVPWM策略中各基本电压矢量的作用顺序.表5 为参考电压矢量落在扇区A 不同小三角形区域时,在一个周期内,各基本电压矢量的作用顺序.由表5 可知,采用基于调制比跟踪的VSVPWM 策略时,每个小三角形区域中的电压矢量包含所有的基本电压矢量,且所有电压矢量的作用顺序遵循相邻两个开关状态之间只有一相的状态发生变化,并且只在P和O或O和N之间变化的开关规则.

表5 A扇区各小三角形区域中电压矢量作用顺序Tab.5 Voltage vector action sequence of each small triangle region of sector A
图9 为参考矢量在A3小三角形区域时,S1a-S2a、S1b-S2b、S1c-S2c的PWM 信号.由于S1a、S3a互补导通,S2a、S4a互补导通,所以通过求反,由S1a、S2a开关信号可以直接得出S3a、S4a开关信号;同理,可以得出S3b、S4b,S3c、S4c的开关信号.由图9 可知,在一个开关周期内,各开关对应的PWM 脉冲沿Ts/2 轴对称,且最多分别开通/关断一次,非常容易由微控制器(如单片机、数字信号处理器等)实现.开关矢量在其他扇区、其他小三角形区域时,具有相同的特性.综上所述,从工程角度看,本项目所提出的调制策略具有较强的实用性 .
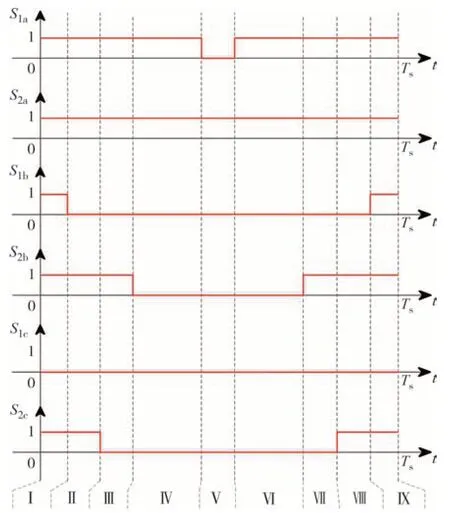
图9 S1a-S2a、S1b-S2b、S1c-S2c的PWM脉冲Fig.9 PWM pulse of S1a-S2a、S1b-S2b、S1c-S2c
此外,由所设计的基于调制比跟踪的VSVPWM策略可知,该方法只需计算三个小三角形区域的作用时间与开关矢量作用顺序,因此简单,能够大幅减小调制算法的计算量.
3 中点电压平衡
在3L-NPC变换器中,钳位电容电压不平衡是由于流入和流出钳位中点的不平衡电流造成的.当采用SVPWM 策略时,大矢量和零矢量引起的中点电流为零,中矢量和小矢量引起的中点电流可为正也可为负.图1 中,定义流出中点为io1一致电流方向、流入中点为io1非一致电流方向,得到中矢量和正、负小矢量及其开关状态对应的中点电流信息如表6所示.由表可知,每对正、负小矢量引起的中点电流方向相反;中矢量引起的中点电流方向取决于负载电流的方向.
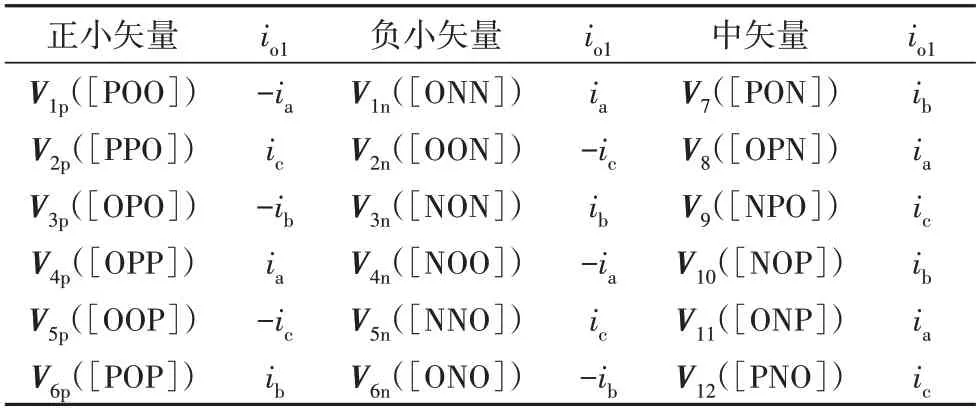
表6 中、小矢量产生的中点电流Tab.6 Midpoint currents of medium and small vectors
在所提出的调制策略中,矢量作用产生的钳位电容电压差与中点电流满足如下关系式:
式中:ΔVo1为两个钳位电容电压差值的变化量;C是单个钳位电容的电容值.
由式(7)可知,采用所提出的VSVPWM 策略,当矢量V落在任意扇区、任意小三角形区域时,ΔVo1在一个周期内的变化量计算公式如下:
式中:Tus、Tls、Tm分别为正、负小矢量,中矢量在一个周期内的作用时间;ius、ils、im分别为正、负小矢量,中矢量单独作用时,中点电流在一个周期内的值.
在三相交流电平衡工况时,发电机输出三相交流电流满足如下关系:
根据式(8)、式(9),得到V落在A、B 扇区的不同小三角形区域时调制策略产生的钳位电容电压差,分别如表7、表8 所示.其中,Tx_Ay、Tx_By分别为A、B 扇区,y 小三角形区域中,基本三矢量中矢量x的作用时间,其中,x可以取1、2、3.

表7 A扇区时的Δ(ΔVo1)Tab.7 Δ(ΔVo1)in sector A

表8 B扇区时的Δ(ΔVo1)Tab.8 Δ(ΔVo1)in sector B
为了使中点电压平衡,本文令第n次采样得到的钳位电容电压差Δuc(n)与第n+1 次VSVPWM 策略产生的Δ(ΔVo1)(n+1)满足如下关系:
采用本项目所提出的基于调制比跟踪的VSVPWM 策略时,q=m,所以,根据式(10)、表7 与三相电流即可确定参数p、r、s的值.此外,为了避免窄脉冲,p取值小于0.8 且大于0.2,r、s的取值小于0.8q且大于0.2q,其他扇区中参数p、r、s的计算方法与此类似.
传 统VSVPWM 中,s=r,由表7可知,此时在A2~A4区域,虚拟中矢量对钳位电容电压没有影响,因此传统VSVPWM 策略的钳位中点电压平衡能力差.在本文所提出的VSVPWM 策略中,s≠r,因此具有更强的矢量调节能力以及中点电压平衡能力.
由表8 可知,B 扇区中,中点电压与s、r无关,表明当V落在B 扇区时,改变s、r无法改变钳位电容电压差,只能通过调节p调节中点电压.因此,相比于A扇区,参考矢量在B 扇区时的中点电压调节能力相对较弱;同理D、F 扇区的中点电压调节能力弱于C、E扇区.
因为扇区A、C、E 具有相似的性质,所以通过扇区A的坐标平移变换可以直接得到C、E扇区中p、s、r的计算方法.同理,在B、D、F 扇区,通过扇区B 的坐标平移变换可以直接得到D、F 扇区中p、s、r的计算方法.
4 仿真实验验证
为了证明本文所提出的基于调制比跟踪的3LNPC 变换器VSVPWM 策略的正确性和有效性,本文搭建了基于Matlab/Simulink 的3L-NPC 变换器仿真模型,并进行了仿真实验,仿真参数见表9.

表9 3L-NPC变换器Matlab/Simulink参数Tab.9 Parameters of 3L-NPC converter in Matlab/Simulink
图10为m=0.9时,小三角形区域与时间的关系,表明参考矢量只在小三角形区域3、4之间交替变化.

图10 m=0.9时的小三角形区域Fig.10 Small triangle region when m=0.9
图11(a)为采用传统VSVPWM 调制策略时,线电压的THD 图,此时线电压的THD 为43.18%.图11(b)、图11(c)为采用本文所提出的基于调制比跟踪的VSVPWM 策略时,线电压的THD 图.图11(b)中,m=q=0.9、THD 为36.64%;图11(c)中,m=0.9,q=0.99THD,为39.49%.显然,采用本文所提出的基于调制比跟踪的VSVPWM 策略可以显著降低线电压的THD值.

图11 3L-NPC线电压THD图Fig.11 THD of line voltage in 3L-NPC
m不变时,采用本文所提出的基于调制比跟踪的VSVPWM策略产生的线电压THD与q之间的关系如图12 所示,其中,m=0.9.由图12 可知,当m确定,q变化时,线电压THD 存在一个最小值点,当q取0.9约等于m时,得到最小的线电压THD.图13 为3LNPC 变换器最小线电压谐波对应的q与m之间的关系,由图13 可知,当m=q时,取得最小线电压谐波.显然,仿真结果证明本文所设计的基于调制比跟踪的VSVPWM策略是正确有效的.

图12 q取不同值时的线电压THDFig.12 THD of line voltage when different q is implemented
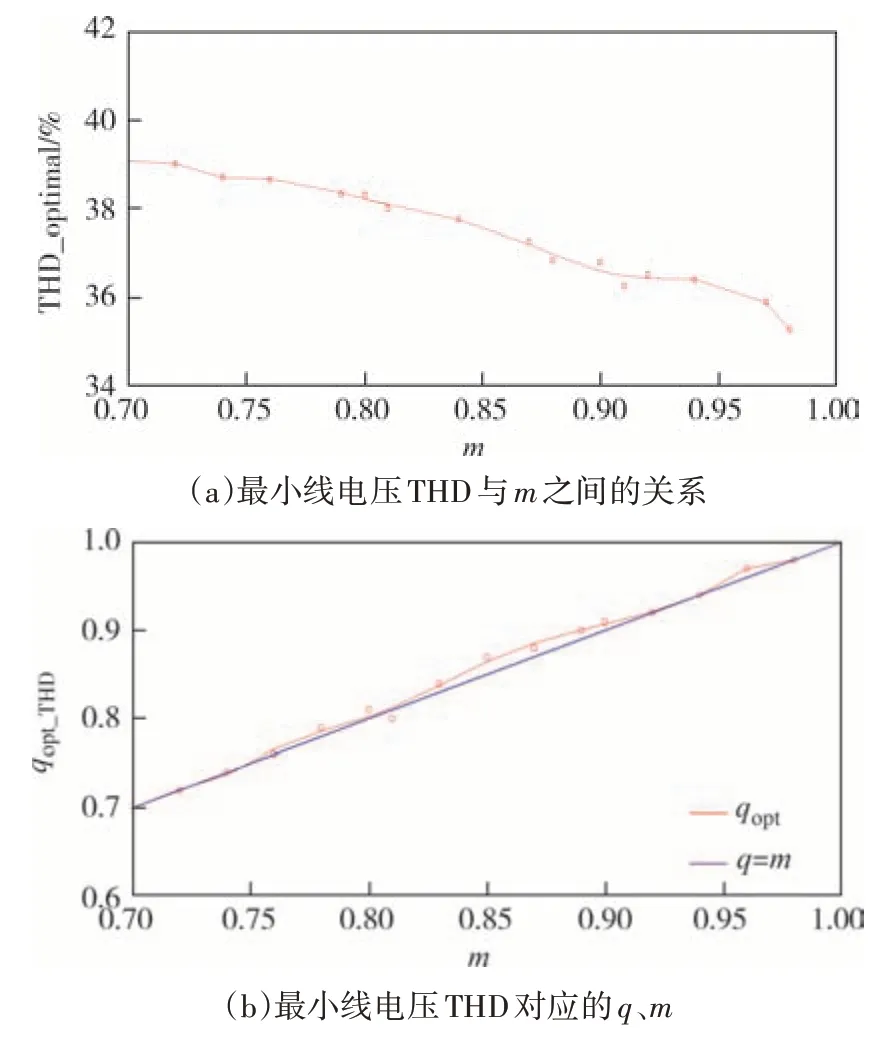
图13 最小线电压THD与m、q之间的关系Fig.13 Relationship between minimum THD of line voltage and m,
图14、图15为3L-NPC 变换器相电压、线电压波形图,其中m=q=0.9;图16 为m=0.57时的线电压波形.由图14~图16 可知,仿真实验得到的电压、电流波形与理论分析一致.
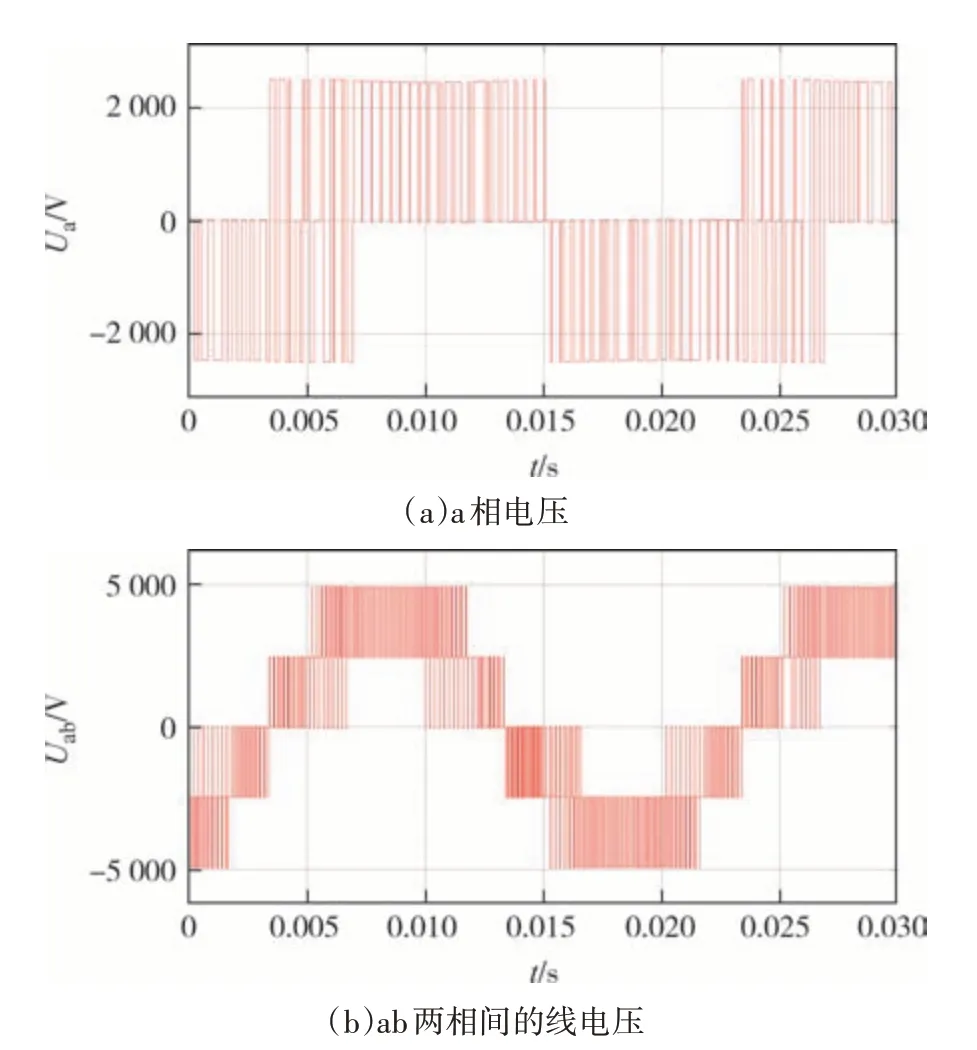
图14 m= q=0.9时的相电压、线电压Fig.14 Phase voltage and line voltage when m= q=0.9

图15 m= q=0.9时的三相相电流、线电压Fig.15 Phase currents and line voltages when m= q=0.9
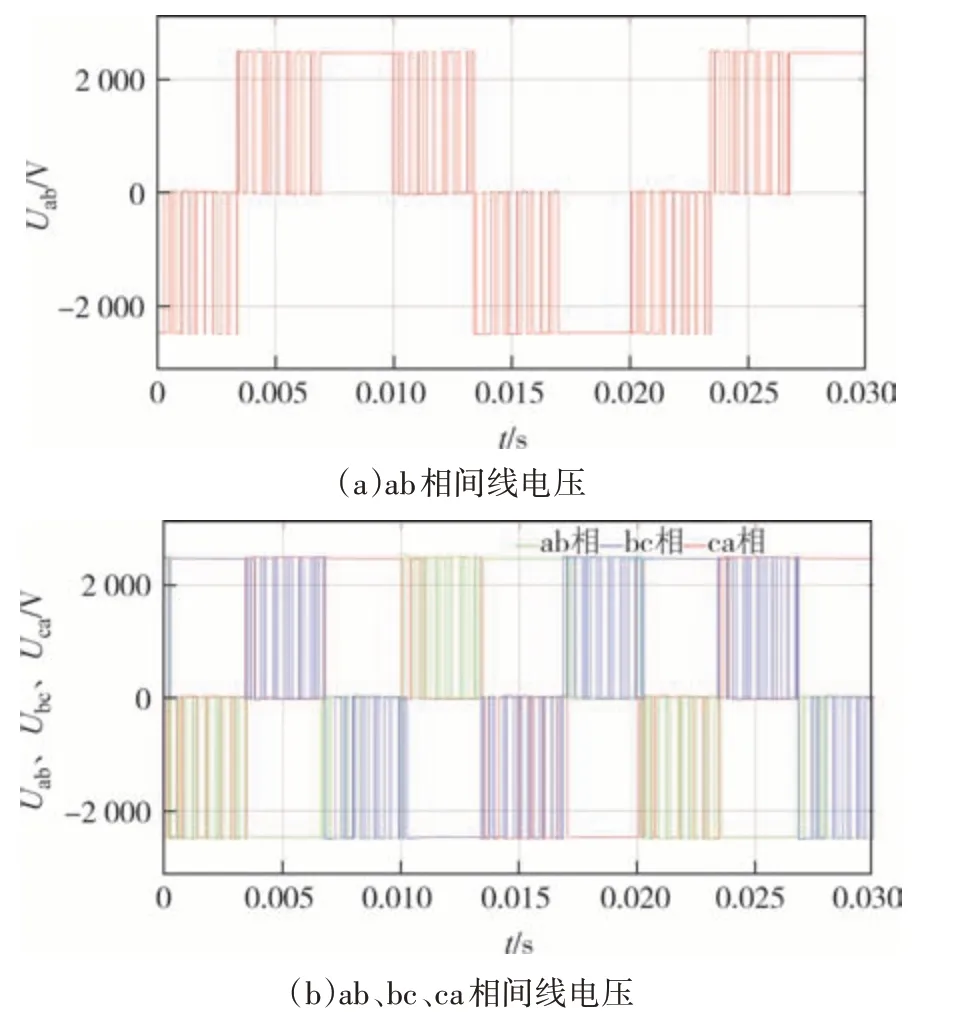
图16 m = 0.57时的线电压Fig.16 Line voltages when m = 0.57
图17 为采用本文所提出的基于调制比跟踪的VSVPWM 策略,且q=m=0.9 时,不同扇区对应的钳位电容电压波形.由图可知,B、D、F 扇区对应的钳位电容电压差较大,表明这些扇区的中点电压调节能力较弱,与本文理论分析结论一致,且中点电压波动幅度=15/5 000=0.3%,在常规工程要求范围之内.

图17 钳位电容电压与扇区Fig.17 Voltages of the clamped capacitors and sectors
图18 为采用本文所提出的基于调制比跟踪的VSVPWM 策略,且q=m=0.9 时,参考矢量在A3区域时,S1a~S4a在一个周期内的PWM 脉冲.由图可知,这些PWM 脉冲与本文的理论分析结论一致,表明本文所提出的VSVPWM 策略容易在单片机、数字信号处理器等硬件平台上实现.
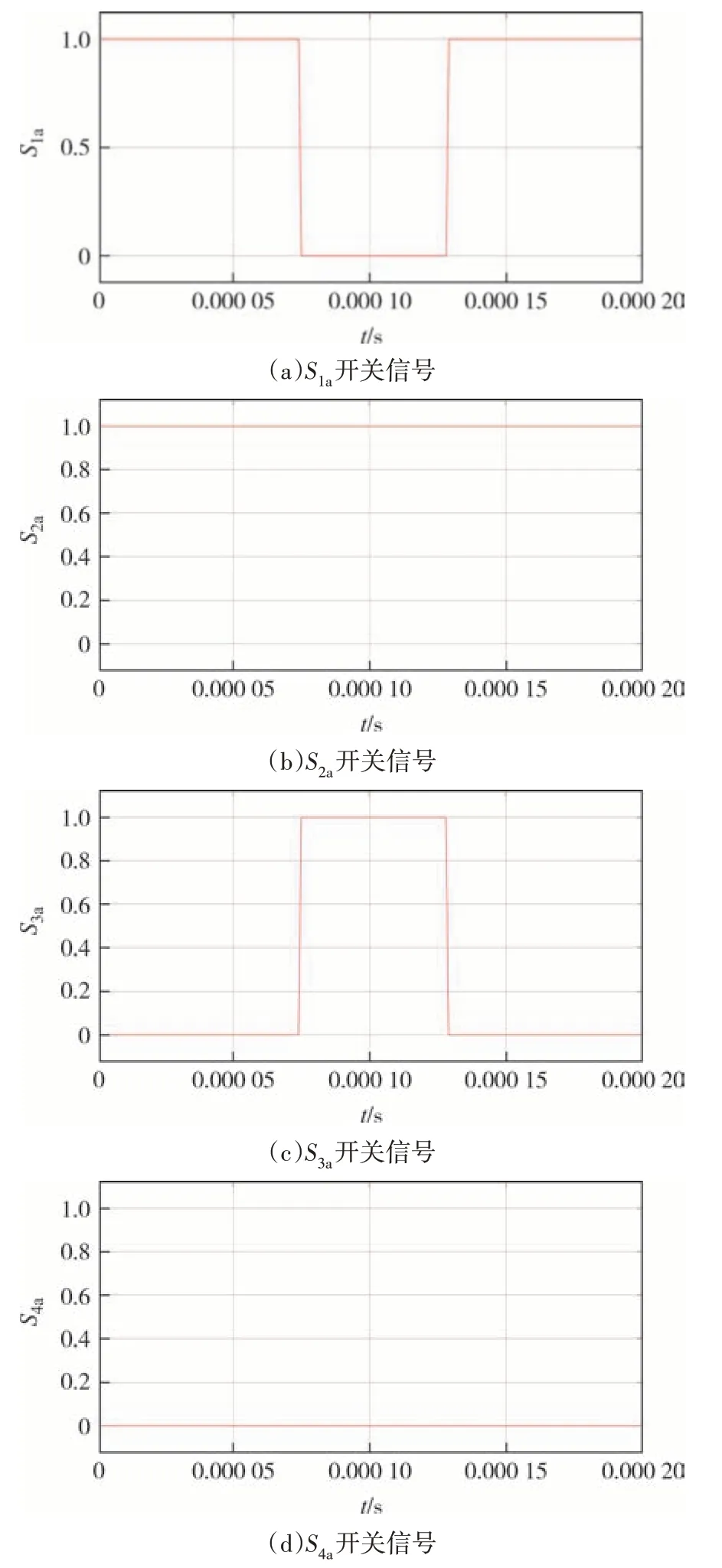
图18 S1a~S4a在一个周期内的PWM脉冲Fig.18 PWM pulse of S1a~S4a in a cycle
5 结论
本文针对采用传统VSVPWM 策略的三相3LNPC 变换器交流侧线电压谐波污染严重的问题,提出了一种基于调制比跟踪的VSVPWM 策略;通过分析调制比与虚拟中矢量之间的关系,提出了一种优化线电压谐波的方法;并在Matlab/Simulink 仿真平台上对该方法进行了仿真实验验证.理论分析和仿真实验结果表明,相比于传统SVPWM 与VSVPWM策略,所提出的VSVPWM 策略简单、有效;当虚拟中矢量幅值与传统中矢量幅值的比值等于调制比时,线电压总谐波畸变率取得最小值;所提出的调制策略能够有效地控制中点电压.

