基于智能优化算法的新能源AVC策略研究

朱子义 王 悦 吴火蓉 尹朝娜

（海南电网有限责任公司信息通信分公司，海南 海口 570000）

随着技术发展，关于新能源AVC 策略的研究逐渐增多。周文俊等[1]研究了考虑风电场调控裕度的风火打捆直流外送系统无功电压紧急控制策略。王耀翔等[2]研究了考虑风电机组无功潜力的风电场无功电压控制策略。柴赟等[3]研究了考虑调压裕度的风电场无功电压控制策略。郜建良等[4]研究了特高压电网无功电压控制策略迭代求解方法。高波等[5]研究了基于改进粒子群算法的电网系统无功电压控制。白迪等[6]研究了基于可控等效阻抗的能量路由器无功电压控制策略。李德鑫等[7]研究了基于自适应模型预测算法的光伏并网逆变器无功电压控制策略。李小菊等[8]研究了动态无功电压控制对频率振荡的影响及附加阻尼控制。鲍金雨等[9]研究了基于模型预测控制的风电场无功电压协调控制策略。这些研究表明，智能优化算法在新能源AVC 策略中具有潜力，可以提高系统的稳定性和鲁棒性。

1 模型构建

1.1 设计思路

该文的设计思路是基于智能优化算法，以全网网损最小化为目标函数，建立新能源自动无功控制（AVC）策略。通过优化目标函数和满足约束条件来实现电力系统经济运行和优化的目标。该设计思路包括以下4 个要素：1） 构建目标函数。选择全网网损最小化作为目标函数。该目标函数综合考虑了电力系统中节点之间的电导、电纳和相角差，通过优化使全网的网损最小化。最小化网损可以提高系统的能源利用效率，降低潮流损耗，从而实现电力系统经济运行的目标。2） 设置约束条件。为了满足电力系统的物理约束和运行要求，需要设置一系列约束条件。这些约束条件包括有功功率的平衡、无功功率的平衡、节点电压的限制以及发电机无功功率的上/下限。设置约束条件可以确保系统的稳定性和安全性，避免出现电压偏离过大、潮流超载等问题。3） 选择智能优化算法。该文将采用先进的智能优化算法求解全网网损最小化问题。常见的智能优化算法包括遗传算法、粒子群算法以及模拟退火算法等。这些算法具有全局搜索和适应性调整的特点，可以有效地搜索最优解。选择合适的智能优化算法可以提高AVC策略的优化效果和计算效率。4） 参数设置和算法调优。当应用智能优化算法时，需要合理设置算法的参数并对算法进行调优。参数设置的合理性和算法的调优将直接影响算法的搜索能力和收敛性。通过调整和优化算法参数可以进一步提高AVC 策略的性能和效果。

综上所述，该文的设计思路是基于智能优化算法，以全网网损最小化为目标函数，建立新能源AVC 策略。通过优化目标函数和满足约束条件可以实现电力系统经济运行和优化的目标。进一步的研究将涉及参数设置和算法调优，以验证该策略在实际电力系统中的有效性和可行性。

1.2 参数设置

首先，假设节点的电压如公式（1）所示。

式中：V为电压幅值；θ为电压相角。

根据复数表示的功率P如公式（2）所示。

式中：I*为电流的共轭复数。

电流如公式（3）所示。

式中：I为电流幅值；δ为电流相角。

根据欧姆定律，电流和电压之间的复数关系如公式（4）所示。

式中：Z为节点的阻抗。

将复数表示的电压和电流代入功率公式，得到公式（5）。

根据指数形式的欧拉公式，将复数形式转换为三角形式，得到公式（6）。

将公式（1）和公式（3）代入公式（6），得到公式（7）。

将公式（1）和公式（3）为实部和虚部的形式，如公式（8）所示。

式中：G为电导，G=Icos（θ-δ）；B为电纳，B=Isin（θ-δ）。

通过类似的推导，可以得到无功功率Q，如公式（9）所示。

1.3 构建目标函数

将目标函数设置为全网网损PLOSS，如公式（10）所示（模型寻求该目标函数的最小化）。

式中：Vi和Vj分别为i和j（j∈i为与节点i相连的所有节点）2 个节点的电压；Nb为支路数量；Gij、Bij和δij分别为i和j节点之间的电导、电纳和相角差。

模型寻求该目标函数的最小化。

通过优化目标函数可以确定发电机机端电压的调整方向，使全网的网损最小化。这种无功控制策略可以在高压输电网络中提高运行效率。与此同时，模型包括相应约束条件。

其中，有功功率Pi如公式（11）所示。

无功功率Qi如公式（12）所示。

电压限制如公式（13）所示。

式中：Vimin、Vimax分别为节点i的电压下限、上限。

发电机无功的上、下限如公式（14）所示。

式中：QGi为节点i对应的发电机无功功率；QGmin、QGmax分别为节点i的发电机无功功率下限、上限。

2 模型分析

2.1 算法介绍

退火算法是一种基于模拟退火过程的优化算法，模拟了固体退火过程中的原子热运动行为。它广泛应用于求解组合优化问题和全局优化问题。

退火算法的基本思想是通过逐步降低系统温度来逃离局部最优解，以期望找到更优的解。退火算法中最关键的部分是如何接受或拒绝新解的过程。Metropolis 准则根据新解的目标函数差值和当前温度来计算接受概率，如公式（15）所示。

式中：P（s→s′）为接受概率；ΔE为目标函数差值；T为当前温度。

通过不断降低温度，退火算法可以逐渐降低接受差解的概率，从而在搜索过程中逐步趋向全局最优解。

2.2 设置目标函数

首先，导入模型的目标函数。忽略节点间差异性，将公式（10）转化为简明的电导、电纳和相角差间关联，如公式（16）所示。

公式（16）表示节点电导G对应的相角δ经过反余弦函数转化。在电力系统中，电导可以度量电流随电压的变化率，而相角表示电流与电压之间的相位差。因此，x1可以理解为节点电导对应的相角的一种度量，它可以反应电导对电压相位的影响。

其转换如公式（17）所示。

公式（17）表示节点电纳B对应的相角δ经过反正弦函数转化。电纳可以度量电压随电流的变化率，而相角表示电流与电压之间的相位差。因此，x2可以理解为节点电纳对应的相角的一种度量，它可以反应电纳对电压相位的影响。

因此，目标函数如公式（18）所示。

式中：y为目标函数，表征电网的网损情况；cosx1、sinx2分别为节点电导、电纳对应的相角在三角函数中的值，这反映了它们对电压相位的调节能力和方向。

该变换可以将电导和电纳的影响以更清晰、更直观的方式体现出来，从而更好地理解电力系统中相角与有功无功功率之间的关系。

将该目标函数导入MATLAB 进行可视化处理，如图1所示。

图1 目标函数随x1 与x2 波动

在该模型中，x1与x2的分布情况共同构成了底部平面，灰度与高度则共同表征目标函数y值的波动情况。其中，目标函数表现为不连续的波峰分散分布，波谷联系而形成显著落差。因此，模型的目标函数曲面可以勾勒其总体特征，设置目标函数求取最小值，再设置参数。

2.3 参数设置

设置系统的初始化参数：1） 初始解。x0=[0.5，0.5]。初始解是算法开始搜索的起点，这里设置为[0.5，0.5]，即变量x的初始值为0.5。初始解应该位于问题解空间的合理范围内，以增加找到最优解的可能性。2） 初始温度。T0=100 ℃。初始温度是模拟退火算法的起始温度，可以控制接受差解的概率。较高的初始温度可以增加算法在搜索空间中跳出局部最优解的可能性。3） 结束温度。Tf=10-6℃。结束温度是模拟退火算法的终止条件之一，当温度降至结束温度以下时，算法终止。较低的结束温度可以提高算法的搜索精度，但是也可能导致算法过早陷入局部最优解。4） 退火率。alpha=0.90，退火率是控制温度下降速度的因子。alpha的取值通常为0.80～0.99，较小的退火率可以降低温度下降的速度，提高算法在搜索空间中的探索能力。

设置参数的目的是在算法执行过程中平衡全局搜索和局部搜索的能力。合理选择初始解和初始温度可以帮助算法在搜索空间中广泛探索。结束温度和退火率可以控制算法的搜索精度和搜索速度，从而在可接受的时间内找到较优解（需要根据具体问题的特点和要求进行参数调优，以达到更好的优化效果）。

3 结果分析

导出模型分析结果，如图2 所示。可视化结果通过等值线图展示了优化过程中的初始解和最优解的变化。由图2 可知，初始解位于等值线的高处，在（0.5，0.5）位置出发，而最优解则位于等值线的低处，即波谷中心。这说明退火算法的优化过程可以通过降低温度来逐渐逃离局部最优解，最终找到全局最优解。模型最终获得最优解，此时x1=17.2873、x2=3.1403，对应的y值为-2（y值已达到最低值），结果证明退火算法在解决组合优化问题和全局优化问题中的有效性。也说明了模型设置了合适的算法参数，包括初始解、初始温度、结束温度和退火率等。与此同时，模型也验证了设计思路的合理性。通过优化目标函数，模型降低了电力系统的潮流损耗，提高了能源的利用效率。通过调节节点电导和电纳对应的相角，其新能源AVC 策略可以提高对电压相位进行调节、优化方向的能力，以确保网损达到最小化。

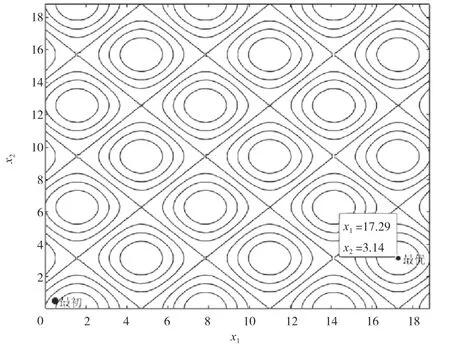
图2 最初解与最优解

新能源的大规模接入给电力系统带来了更大的不确定性和复杂性。AVC 策略需要考虑电力系统的稳定性和可靠性。智能优化算法可以有效地处理复杂的约束条件和优化目标，帮助找到最优的控制策略，提高电力系统的稳定性和可靠性。现有新能源AVC 策略的设计目的是通过优化全网网损最小化的目标函数来降低电力系统的潮流损耗、提高能源的利用效率。智能优化算法（例如退火算法）可以帮助寻找全局最优解，实现电力系统经济运行的目标。通过优化电力系统的运行状态可以降低能源成本、提高供电质量，并最大程度地满足用户需求。

4 结语

该文通过基于智能优化算法的新能源AVC 策略的设计思路和模型分析，成功地建立了优化模型并得到最优解。作为一种全局优化算法，退火算法在新能源AVC 策略中展现了其强大的搜索和优化能力。通过优化全网网损最小化的目标函数并满足约束条件，降低了电力系统的潮流损耗，提高了能源的利用效率。未来可以进一步改进和扩展退火算法，以适应更复杂和多样化的电力系统需求。同时，可以结合其他智能优化算法和控制策略，进一步提高系统的性能和稳定性。