基于多目标遗传算法的服装柔性车间装配线平衡优化
朱 毅 朱玉杰
(东北林业大学,黑龙江 哈尔滨 150000)
随着消费者对服装产品个性化、多样化需求的不断增加,服装企业必须快速响应市场变化,提供个性化定制服务,以满足消费者的需求。与传统的大批量生产相比,个性化定制趋向于小批量多品种(SBMV)生产模式,要求在服装生产中充分发挥工艺柔性和设备柔性。由于采用SBMV 生产模式,因此悬挂式装配线在换装过程中面临装配线平衡(ALB)问题和机器分配问题。ALB 涉及的工艺路线优化问题是预生产排程的核心问题,属于柔性车间排程问题[1]。通过优化装配线工艺分配和机器分配方案可以最大限度地提高整条装配线的效率和柔性。
针对服装装配线的平衡优化问题,该文提出一种多目标遗传算法(MOGA),以实现装配线排序效率最大化和机器调整路径最小化的目标[2]。通过服装车间的生产实例验证MOGA 配制方案的有效性,MOGA 既可以实现流水线平衡的常规优化目标,又可以满足小批量多品种生产模式下快速换装对机器调整路径最小化的优化要求。MOGA 为企业设计实际生产线的人机调度方案提供参考。
1 数学模型
单件流服装装配线规划问题属于多工艺路线柔性车间排程问题,可以描述为每个工件有多条工艺路线。每个工件包括n道工序,这些工序必须依次经过m个工位才能完成服装缝制任务。
考虑工位数量和机器数量的限制,单件服装车间装配线问题的约束条件如公式(1)~公式(6)所示。
式中:n为工件总数;m为加工站总数;p为总目标;yj为工作站是否使用(j为0 表示未使用,j为1 表示已使用);mji为机器类型i是否可用于工作站加工(j为0 表示不可用,j为1 表示可用);xijk为在工作站第k次操作的处理时间。
公式(1)表示每个工作站最多包括2 种机器,公式(2)表示1 个工作站同时只能加工1 个工件,公式(3)表示一项操作最多只能部分加工1 次,公式(4)表示1 个工序只能在1 个工作站的1 台机器上加工,公式(5)表示每个作业的所有操作都必须完成,公式(6)表示处理时间总是非负的。
在生产过程中,流水线指标可以评价流水线的平衡状态,判断计划能否保证准时交货。以多目标算法求解FCALBP为目标,采用装配线平衡率最大化和换装过程中机器调整路径最小化的优化目标建立数学模型,如公式(7)~公式(9)所示。
式中:E为装配线的整体效率;Eej为每个工位的生产效率;m为加工站总数;Tj为j站的工作时间;Tbs为计划中总处理时间最长的站的处理时间。
第二个优化目标是找到最小的机器调整路径。在小批量多品种服装生产模式下,为了实现快速换装生产,流水线需要能够快速、有效地切换生产工艺。采用目标函数计算装配线上所有机器的调整距离总和R,如公式(10)所示。
式中:Sk为装配线上机器的调整路径;S'k为同一机器在新装配线机器布局方案中的位置;Sk'为在新的流水线机器布局方案中需要补充或移除的机器移动路径长度。
2 多目标遗传算法
2.1 编码和种群初始化
2.1.1 编码方法
当采用遗传算法研究传统生产线平衡问题时,通常使用二进制编码进行编码和解码。在FCALBP(局部二值模式)中,使用二进制编码可能会破坏服装工序之间的优先级关系,从而导致解的不可行。而面向对象的编码方法可以将该问题的可行方案表示为染色体,并使子染色体继承父染色体的特征。因此,MOGA 采用路径表示法对布料工序进行编码,生成工序染色体。工艺染色体的长度等于1 件服装的工艺总数,每个工序基因携带相关的工序信息,例如后续工序、标准工时和机器型号等。MOGA 包括2 个染色体群,即工序染色体和计划染色体。2 个种群中的染色体数量始终相同,并且它们之间建立了一对一的映射关系。工序染色体种群考虑工序之间的约束关系,并采用遗传算法进行操作,例如选择、交叉和变异等[3]。时间表染色体种群由过程染色体种群通过过程分配机制产生,可以计算MOGA 的适应度值并将其反馈到过程染色体选择阶段。
工序分配机制根据工序染色体考虑工位数量和每个工位单个工件的可分配作业时间进行相应的工序分配。如果瓶颈工时始终存在于同一个工位,就会导致挂线拥塞。在分配过程中,一些工序被批量分割,以便在2 个不同工位进行周期性加工,从而优化装配线的瓶颈工位。在应用工序分配机制后,将生成与工序染色体唯一对应的计划染色体,该染色体包括每个工位的工序和分割工序信息,可以进一步解码,以获得包括工序和机器分配信息的调度计划。
2.1.2 种群初始化
服装流程图的结构与有向无环图相同,所有服装工序的调度与有向无环图的遍历具有共同特征:所有顶点都会出现且只出现1 次(加工的唯一性)。如果存在从顶点一到顶点二的路径,那么在排序中,顶点一必须在顶点二的前面(工序约束)。1 个顶点可以指向多个顶点,也可以被多个顶点指向(处理的灵活性)。
MOGA 利用随机拓扑排序进行群体初始化。拓扑排序确保在不违反服装工艺约束的情况下对服装工艺进行排序并生成工艺染色体。该文在拓扑排序过程中引入随机算子,保证初始种群在整个可行解空间内生成,从而提高MOGA 的全局搜索能力。具体步骤如下:1) 定义约束关系。根据工艺流程和工艺信息定义顺序约束。2) 生成流程依赖图。根据所有流程的顺序约束进行排列,构建有向无环图(DAG)。图中的每个节点代表1 个流程,边代表流程之间的依赖关系。3) 拓扑排序。采用随机拓扑排序算法对流程依赖图中的节点进行排序。选择1 个入度indegree(指有向图中某点作为图中边的终点的次数之和)为0 的节点作为起点,开始遍历相邻节点。当访问1 个节点时,如果其indegree为0,就根据随机算子决定是否在结果列表中添加1 个元素。如果是,就删除其指向的所有边;否则,继续遍历其他节点。重复步骤三,直到访问完所有节点。4) 生成过程染色体群。节点列表即为过程染色体,根据种群大小初始化种群[4]。

表1 工艺信息
MOGA 中编程染色体的生成步骤如下:1) 工序定位。除第一个工序外,当其他工序被视为待分配工序时,先确定所有工序分配的工位。工序被定位在最后一个工作站并进行进站判断。2) 进站判断。在工序分配机制中,进站判断包括机器类型判断和工站工作时间判断。当站内机型数为0 或1时,直接测量工作时间[5]。如果工作时间满足要求,那么工序可以进入工位,同时更新工位机器类型和工作时间。如果工作时间不符合要求,那么进入步骤三。当站内机器数量为2 台时,判断待处理工序对应的机器与当前站内机器是否一致,以便进行工作时间判断。如果不一致,就进入下一站执行步骤二。3) 批量工序分配。当工作时间不满足要求时,根据公式(1)中描述的约束条件进行分批。根据剩余工作时间与当前工序时间的比例确定分割比例,取值接近1/n或(n-1)/n,如公式(11)所示。4) 重复步骤一~步骤三,直到过程染色体上的所有过程基因都进入过程基因组。
式中:Tj为工位的实际生产速度;T'j为已进站工序的总工作时间;Ti为可分割工序的加工时间(分批加工将整批工件中的第i道工序在2 个工位之间按一定比例周期性地分配加工);Rp为单个工件工序不能分到2 个工位加工[6]。
2.2 选择操作
在整个MOGA 迭代过程中,将规划染色体的联合适配值作为染色体的评估标准。装配线的有效适配值和机器调整路径的适配值被赋予不同的权重。对机器调整路径最小化的结果进行归一化处理,以生成机器调整路径的适配值。
最佳人员配置计划包括在保持装配线原有机器布局的情况下实现高效生产的目标[7]。然而,在实际应用中,为了提高装配线的更换效率,可能需要调整某些机器。机器调整路径采用最大/最小归一化方法进行处理,将路径特征的范围控制在0~1。
在多目标遗传算法的迭代过程中,采用精英保留策略保留性能优越的个体,以加速算法收敛并提高解的质量。具体来说,在每代种群中,将适配度前40%的染色体作为当前种群的精英群体,为下一代产生后代。
此外,从解集中选择染色体也是提高搜索性能的重要方法,根据装配线效率和机器调整路径等其他标准,从解集中选择2 个子集,每个子集占种群总数的10%,并与前一个精英组组合成新一代后代。这样的操作可以综合考虑多个标准,有助于找到更好的解决方案。
2.3 改进交叉和变异操作
2.3.1 交叉操作
交叉操作在遗传算法中起关键作用。服装工艺之间的约束关系非常复杂,直接进行交叉操作会破坏子染色体工艺基因之间的约束关系。该文采用约束调整方法对交叉操作进行改进,保证子染色体的有效性。前端点g1和后端点g2交叉基因段的前端点和后端点是随机产生的。端点前的子串和端点后的子串g1和端点后的子串g2保留2 个亲本过程染色体(P1,P2)。g1和g2之间的交叉基因段被交换,基因段中的相同基因保留原来的交换顺序。在验证约束关系后,根据后续程序的基因位置将差异基因插入适当的位置。
满足约束关系的父染色体(P1,P2)如图1 所示。在两点交叉操作中,断点g1和g2先被选中。交换中间子串中的相同过程3、4、6 和7 并保留各自父本中的基因顺序进行交叉。P1子串中的差分基因为8,其子代的插入点在过程基因7~基因9。子串中的差异基因为P2子串中的差异基因为2,其子代的插入点在过程基因1~基因3。目前有2 个可选点,随机选择可选点进行插入操作,交集最终产生子代S1和S2。

图1 流程有向无环图
2.3.2 变异操作
在遗传算法中,通过变异操作对染色体基因进行扰动,以保证跳出局部最优解的能力。该文通过改进两点交换法来实现变异操作。在父染色体上随机选取2 个点,将这2 个位置上的基因与子代进行交换。变异操作还利用约束调整方法对不可行解中变异基因的位置进行调整,以保证子染色体的有效性。根据图2 的过程路线生成父染色体,并进行两点交换变异操作,如图3 所示。
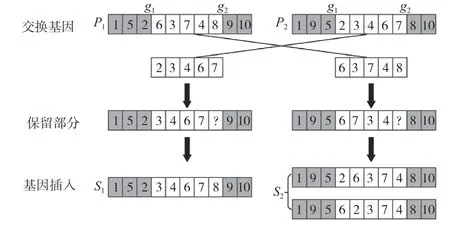
图2 两点交叉示意图

图3 两点交换示意图
3 试验和计算结果
该文以成都某服装公司的工装衬衫生产订单为例。该衬衫包括64 道基本工序,根据衣片的部位可划分为5 个服装模块。工序约束条件如图4 所示。每道工序的相关工序涉及平车、刀车、电脑平车以及四线叠加车等机型。人工操作不需要额外的车站空间,因此不包括在车站机器类型数量的计算中。工序相关信息见表1(工艺编号与图4 的工艺路线图对应)。

图4 衬衫工艺路线图
该案例中的工装衬衫流水线方案以服装车间的人工方案为基础。根据交货要求,日产量为200 件衬衫。工人每天的操作时间为9 h,示例节拍为2.70 min,单件衬衫缝制标准工时为41.49 min,理论上最少工位数为16 个。在悬挂式流水线编排方案生成程序中,设定种群规模为50,那么拓扑排序选择概率为0.5,交叉概率为0.6,变异概率为0.05,工位生产节拍为2.7,最大迭代次数为200 次。
根据不同的流水线工艺分配方法,各工位的加工时间和机型数量见表2。在人工分配方案中,瓶颈工位的加工时间为3.66 min。流水线装配效率为70.93%,包括3 种类型机器的工位比例为43.75%。与人工分配方案相比,MOGA 算法和GA 算法对工位处理时间的控制更严格,并且会限制机器的使用数量。传统GA 对装配线配置的效率为85.05%,瓶颈工位加工时间为2.71 min,与人工分配方案相比,装配线效率大约提高了15%,服装生产线的工位数量通常为16 个、18个、20 个和22 个。由于工位机型数量的限制,因此MOGA和GA 的工位数量有所增加,最终方案的18 个工位仍为正常规模。

表2 工艺站编译方案
MOGA 的联合适配值迭代曲线如图5 所示。在生产过程中,瓶颈工序时间始终存在于同一工位,会造成挂线拥堵。为了改善瓶颈工位,在编程中进行工序入库操作,将部分工序分批入库。相应的工序定期分配到2 个固定工位进行缝制操作,瓶颈工位不会固定在同一位置。在整个缝制阶段,流水线的效率将在一定范围内波动。与传统遗传算法相比,MOGA 进一步提高了流水线效率(与传统遗传算法相比,流水线效率从85.05%升至88.33%),MOGA 在方案编译的染色体生成阶段集成了工序批量拆分机制,进一步提高了装配线效率,MOGA 和GA 的装配线效率迭代曲线如图6 所示。

图5 联合适配性曲线

图6 效率曲线
机器调整路径的迭代曲线如图7 所示。观察迭代过程中的变化曲线可以发现,尽管存在一定的不稳定性,但是机器调整路径可以收敛。传统遗传算法的流水线效率收敛于最优值,但是相应的机器调整路径波动幅度大。在MOGA 中,机器调整路径被赋予权重并进行优化。MOGA 将机器调整路径最小化作为优化目标之一。虽然在迭代过程中因流水线效率的优化会产生一定的波动,但是可以实现总体收敛。在该案例中,MOGA 的最终机器调整路径长度为123 m。

图7 机器调整路径曲线
4 结语
该文针对服装柔性车间小批量多品种生产模式下的排产问题提出了一种解决方案。该方案基于实际生产的约束条件建立了流水线效率最大化和机器调整路径最小化的数学模型。此外,该文通过改进传统遗传算法的种群初始化、交叉和变异过程,开发了多目标遗传算法(MOGA)。基于MOGA 的排产方法利用实际企业订单进行经验验证。结果表明,MOGA 能够优化服装悬挂线的加工顺序,同时满足服装生产中灵活性和设备约束的要求。值得注意的是,与多种服装场景下的人工排布方法相比,MOGA 具有更高的流水线编排效率(超过10%)。MOGA 将机器调整路径作为优化目标之一,以确保迭代过程中的最小值收敛。因此,最终的生产方案能够加快新订单的流水线机器调整速度,减少停机时间,从而满足小批量多品种生产模式的需求。相关结果证明了基于MOGA 的方法通过设计多目标和多优先级组合优化算法来帮助企业实现精益生产目标方面的潜力。
在MOGA 求解过程中,各种参数(包括适配值权重、交叉和变异概率)都会对最终解决方案产生影响。为了进一步优化基于人工智能的柔性制造预排程智能决策系统,将重点关注生产过程中的自主学习、适应和参数调整。该文主要设计MOGA 来执行服装装配线的预调度任务。然而,实际生产过程会受实时限制,例如工人缺勤或机器故障,这就需要对工作流分配进行即时调整。因此,在未来的研究中,需要研究服装作业车间的实时调度,以充分处理突发事件。

