复杂载荷下动态拉杆力测试方法研究

李盼菲，周琦，刘勇，谢双林

（郑州机电工程研究所，河南郑州，450015）

0 引言

拉杆用于支撑重机械的大梁或者前臂，其作用十分重要，拉杆的强度以及安全系数是设备安全性能的重要保障。由于拉杆的强度不足而导致的断裂事故屡见不鲜，因此拉杆的安全系数已经成为重机械安全性能的首要指标。研究拉杆强度的计算方法和测试技术，从理论和实践两方面同时着手来对拉杆强度进行研究，具有十分重要的意义[1]。通过应力应变测试以及力的动态测试结果，可以在一定程度上判断矢稳的大致位置和状态，从而有针对性的进行结构优化设计，来达到提高强度的目的[2]。目前，工程应用上使用压力传感器、多向或单向应变片等来进行应力测量，但是，应力应变的测量通常是在施工现场进行的，拉杆的受力并不是规则和均匀的，其同时受到多种复杂的载荷耦合作用，导致测试十分困难。因此，我们要得到高质量的数据，达到较高的测试准确度，同时能够避开这些复杂载荷带来的测试难度大的问题，需要对测试方法进行进一步的探索和研究。

本试验工况中，某系统使用拉杆进行复杂作用力的传递，期间拉杆随着结构动作上下运动，且运动不在一条直线上，拉杆上承受拉力和压力不规则交替循环。为了测量此拉杆轴向受力情况和弹性变形，判断其是否屈服，需要对其同时进行轴向拉压力和应变测量。由于工作状态的安装空间限制，测量传感器不能安装在杆两端，且重量不能太大，以免干扰拉杆受力情况，因此普通的力传感器不能够满足此试验测试要求。张红星[3]使用应变计埋填法，将应变片埋入螺栓孔中，通过粘合剂进行应变的传递，有效地解决了复杂工况下传感器安装困难的问题；桂永旺等[4]在同一锚杆上使用多种方法测试，指出在复杂受力时应采用多面粘贴应变计的方法进行测试；苏桥等[5]通过电阻应变计和力传感器两种方法对转向横拉杆的受力情况进行测试，来计算最大齿条力，并得出结论，此两种方法用于测力均比较合理。在动态测量环境中，郑韬等[6]的试验证明，应变式力传感器对于高速拉伸载荷震荡有明显改善，因此，本试验使用应变片构造惠斯通电桥来测试拉杆受力情况。

1 测量原理

本试验拉杆是一个一次超静定结构，需要找出变形协调条件，其变形协调条件又不同于一般的固定支座，而是一个拉杆的弹性变形支座位移，并且在安装之后是倾斜的，并不垂直，所以需要先将倾斜力分解，这种不与受力杆件垂直的超静定结构的支座位移并不为零，也就是变形协调条件的变形综合并不为0，因此其不是一般意义的一次超静定结构的力法正则方程。而我们的计算采用解除拉杆约束，代之以力表示，后拉杆的弹性变形量也就是后拉点支座变形的总和[7]。根据本试验件的力学模型，除了自重载荷外，其余的外载荷并非同时作用在拉杆上，也就是说，其作用的位置和作用的方向、时间也有一定的偏差，那么我们计算的时候，分别计算其载荷情况进行线性叠加即可。另外，由于倾斜的拉杆力对其形心产生的附加弯矩不可忽略，我们曾经比较过考虑此弯矩和忽略此弯矩的计算结果，发现差别比较大，所以计算时，虽然比较麻烦，但是我们依然将其考虑在内[8]。在正式试验加载复杂载荷的时候，我们通过贴在拉杆表面的应变片来将轴向应变记录下来，并转化为电阻变化量，利用采集装备再将其转化为电压的变化量，通过信号的调理和放大来进行采集处理，能够最大程度的提高信噪比，获取有用信号。

应变表达式为：

式中：ε 为微应变，Δl 为弹性形变量，l 为杆总长。

在实际测量中，应变量是极其微小的，由应变引起的电阻的变化量也是非常小的，但是电压的变化却较为明显。在工作过程中，拉杆受到拉压力时，其表面的轴向应该是单向应力，但是横向也存在应变，其应变量与轴向应变量有一定的关系，我们把它们之间的比例成为泊松比，用μ 来表示。这个横向应变并不是我们想要测量的，因此，我们需要采取一定的方式将其抵消掉。一般情况下，构建惠斯通电桥，将其横向应变的两个桥臂作为相对桥臂可以抵消。如图1 所示。

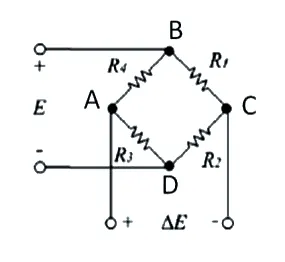
图1 惠斯通电桥

图1 中，四个桥臂电阻分别为R1、R2、R3、R4，我们在BD 两端给全桥电路供电，供电激励电压为E，同时在AC 两端测量全桥电路的输出电压ΔE。本试验应变片采用T 型贴法，相对桥臂的两个应变片R1、R3 敏感栅与拉力方向平行，即轴向，R2和R4 的敏感栅方向与拉力方向垂直，可以消除偏载误差和温度带来的误差[9～11]，如图2 所示。

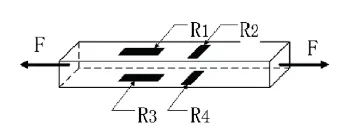
图2 应变片粘贴示意图

图2 中，R1、R3 应变片的敏感方向为轴向，主要用来测量拉杆的轴向应变，是本实验中的工作应变 片。R2、R4 的 敏感方向为横向，与轴向垂直，主要用来补偿和抵消横向应变产生的影响，因此，其为补偿应变。图中F 表示拉杆的轴向受力。其轴向受力是复杂的、动态的多种载荷叠加的结果。在试验中，由轴向作用力F 产生的应变片R1、R3 的应变量为εF，同时考虑到应变片受到温度变化而产生的感应应变量εt，则各个桥臂产生的应变量为：

式中：μ 为拉杆材料的泊松比。

图1 中，在BD 处加激励电压E，AC 点输出电桥电压ΔE。电阻R1、R2、R3、R4 为桥臂电阻，则电桥输出电压表达式为：

本试验中使用四个相同应变片搭建电桥，应变片型号为KFGS-1-120-D17-11L1M2S，应变公式为式(5)。其应变电阻均为120Ω，即R1=R2=R3=R4。应变系数相同，均为2.06，即式(5)中，四个桥臂的K 值相等。

将式(2)(3)(5)带入式(4)中，可得：

通过输出电压ΔE 的变化可以得到轴向作用力F 产生的应变为：

在拉杆的屈服强度内，轴向应变量εF与轴向拉力F 成正比关系，根据式(7)可知，拉杆所承受的拉力与电桥输出ΔE 成正比关系，即：

因此需要对测量系统进行标定得到式(8)中K 与b 值，即可通过桥路输出电压测量拉杆所承受的轴向拉力。

2 系统标定

对前面构建的系统进行标定，首先，根据图中示意将轴向应变片和横向应变片粘贴在拉杆表面，将应变片的线路按照电路图构建全桥电路，在材料机上对拉杆进行标定。我们规定当拉杆受到压缩力时，输出为负，收到拉伸力时，输出为正。

在BD 两端加载电桥电压E 为2.5V，在AC 两端测量桥路输出。将拉杆竖直挂起，标定之前，已经有重力等作用力加载到拉杆上，此时电桥已经有电压输出。在加力之前，将测量系统进行清零处理，即设定b 值为0。因为试验时并没有初始拉力，但采集系统仍具有微小的电压输出，此电压受到环境温度影响并不固定，需要在实验前进行清零操作，即设定b 值为0。

在拉杆上加载拉力，稳定之后记录电桥的输出，通过最小二乘拟合算法，算出K 值。得到测量数据与施加力的关系曲线如图3 所示。

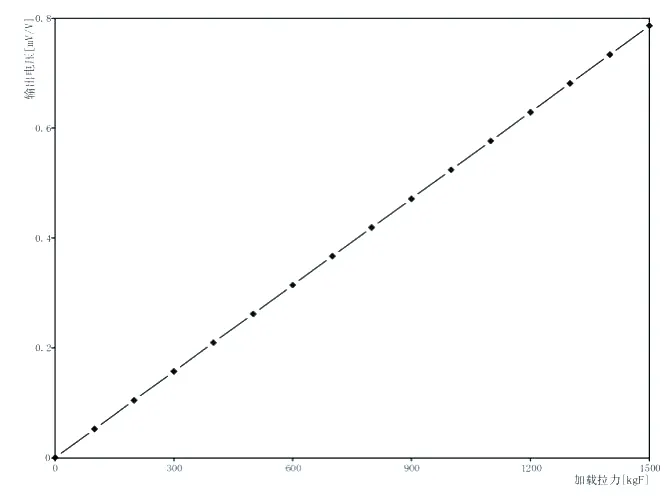
图3 标定数据

根据最小二乘拟合算法，得到k 值为1907.145kgF/mV/V。将标定后的拉杆安装在试验样机上，检查其他参数设置，使之满足试验要求。

3 试验数据分析

为了测试电桥测量方法的稳定性和可靠性，试验时同时在拉杆上测量应变。测量设备使用DEWETRON 公司的DEWE-50-PCI，搭载STG 程控模块进行测试，测量精度高达0.05%。试验进行四次，每次试验开始时对设备进行电压清零操作，即不保留初值。数据如图4 所示。图中曲线S1 为应变曲线，单位为微应变（με），F 为通过惠斯通电桥测出的拉力曲线，单位为公斤力（kgF）。

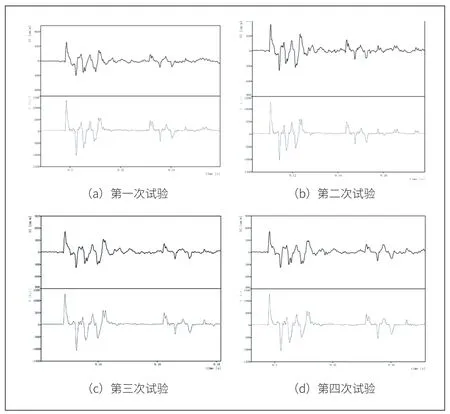
图4 试验测试数据

从上述试验结果可以看出，四次的机构动作基本相同，先是机构拉伸动作，紧接着开始压缩，在拉伸受力和压缩受力之间震荡几次后恢复原状。在此过程中，由于拉力与应力的测量手段相同，因此其频率响应基本相同，从图中可以看出，测量频率范围能够满足机构动作测量需求。四组试验数据中，应变曲线与拉力曲线的幅值基本一致，证明本试验通过应变片组成惠斯通电桥测力的方案可行[12]，同时，也验证了文中式(7)与式(8)的理论正确性。试验中，综合采集设备、标定设备、应变片粘贴误差等，计算出其扩展不确定度为2.24%（k=2）。四次重复试验，曲线一致性良好，且与本结构件的试验状况和预示值基本吻合，证明本次测试数据可信度高，本方案用于工程测试中比较可靠。但是本实验方法也有一定的不足之处，在测量时将拉杆等效为二力杆，而在实际试验中，结构发生平面外变形时，撑杆是弯曲的，应该等效成梁进行计算。

4 结语

由于计算系数时的拟合算法比较复杂，文章省去了其推导和计算的过程，直接给出了计算结果。即便如此，计算和测量过程依然十分复杂。本文利用了先进的设备和计算软件，最终计算出了在实战状态下的应力应变值和拉杆动态受力值，即为各工作状态下的拉杆力大小，由此来验算拉杆的屈服状况。

由以上分析可以知道，本文所采取的使用应变片直接粘贴于结构件表面组成惠斯通电桥测量拉压力的方法，具有很强的可操作性，不会改变拉杆的原始结构及受力状态，并且测量结果精准可靠，能够满足工程应用，对于结构件的后续安装和使用提供了强有力的数据支撑。

本试验方法试验成本低，安装简单，数据可靠性高，测试结果合理，拉压力的测量与拉杆的应变变化规律基本一致，并且有效避开了拉压力传感器安装困难的问题，在大多数复杂载荷、复杂环境的拉压力测试环境中具有极大的优势。