爆破施工对紧邻既有隧道影响的研究
李新翰 LI Xin-han
(江门市安恒爆破工程有限公司,江门 529000)
0 引言
随着人们生活水平普遍提高,车辆保有量也在逐年提高,原有的公路、隧道等基础设施很难满足日益增长的交通运输量需要,更多的改建、扩建、新建工程在全国各地铺展开来。由于地形和环境条件的限制,在实际中,经常出现新建工程与原有隧道临近和上下穿插交错的情况。由于新建工程临近既有隧道,将引发一系列的安全问题,总地来说可归纳为以下两方面[1-3]:①新建隧道的开挖引起岩体应力重分布;②钻爆法相对于其他方法,在开挖成本和施工进度方面依然具有一定的优势,是目前隧道施工的主流方法,其产生的振动等危害效应对既有隧道造成的影响。
国内众多学者也对爆破施工对紧邻的既有隧道影响展开了研究:刘唐利等在研究地铁隧道爆破施工时对紧邻既有隧道的影响时,用ANSYS/LS-DYNA 建立简化后的炮孔模型,计算结果显示,与实测结构吻合度较高[4];康海波等运用LS-DYNA 对隧道内爆轰产物的传播距离、传播规律、超压衰减做了一系列的研究[5];蔡路军等研究上穿公路隧道爆破对下方供水隧道的影响时,分析了爆破作业时产生的应力和振动情况[6]。
1 工程概况
新建隧道分别位于既有隧道左右侧,净距为18.15~25.48m 不等,为单洞四车道隧道,隧道左线长472m,其中进口明洞长10m;出口明洞长10m;隧道右线长346m,其中进口明洞长20m,出口明洞长20m。新建隧道进、出口均为已废弃采石场,坡形陡峭,山体坡角约75°-90°,燕山期花岗岩出露,岩性以Ⅲ级围岩为主,进、出口位置经开采后形成陡坎。新建隧道与既有隧道位置关系如图1 所示。

图1 新建隧道环境图
在爆破施工中,根据所处岩层的围岩性质不同所采用施工方法分别有:二台阶法(上下台阶法)、三台阶法、单侧壁导坑法(CD 法)、双侧壁导坑法。考虑到在施工条件固定的情况下,影响爆破振动主要取决于最大单段起爆药量。由于新建隧道与既有隧道的距离过近,工程靠近既有隧道一侧采用机械开挖,仅远离既有隧道一侧采用爆破开挖,采用电子雷管起爆,每段雷管之间的延时在20-30ms 之间,其中最大单段药量为单侧壁导坑法中左上部隧道的辅助孔起爆,其炮孔布置图如图2 所示,起爆参数见表1。
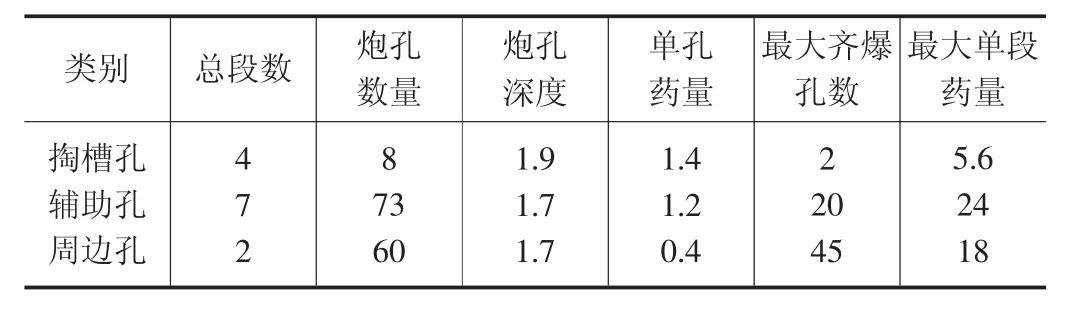
表1 爆破参数汇总表
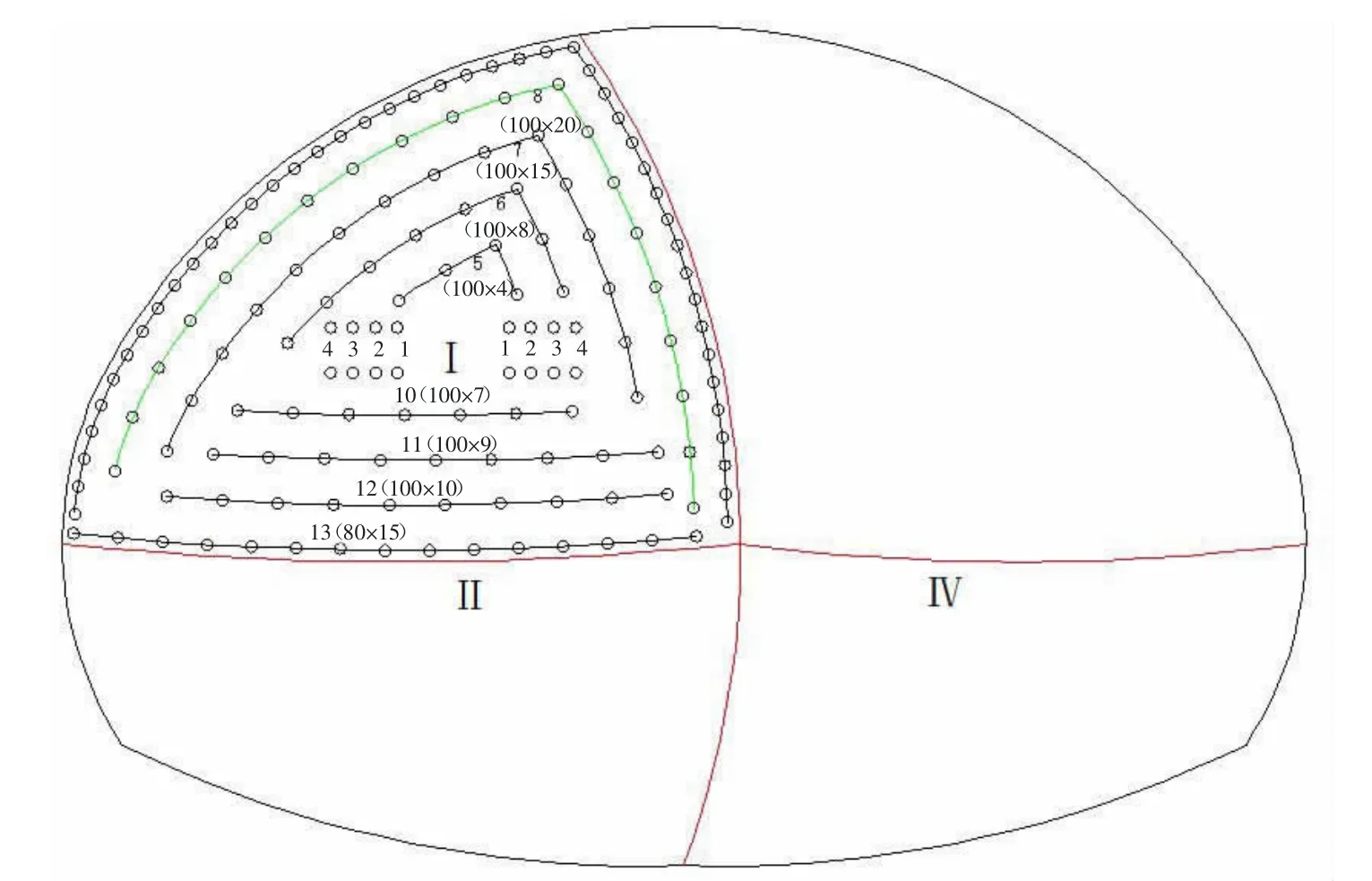
图2 单侧壁导坑法炮孔布置图(部分)
2 爆破振动监测
为确保既有隧道在爆破施工下的安全,在新建隧道左线爆破施工时,进行了数次爆破振动监测。在既有隧道左线布置爆破振动监测点,测点共布置5 个,测点1 位于与新建隧道掘进掌子面平齐的既有隧道左侧,其余测点在既有隧道中沿掘进掌子面前进方向每隔5m 布置一个。其中x 方向为垂直于隧道走向的水平方向,y 方向为平行于隧道走向方向,z 方向为垂直于隧道走向的竖直方向。测点布置示意图如图3 所示。
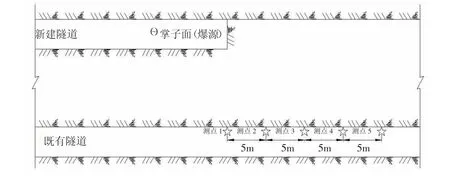
图3 爆破振动监测点布置示意图
由于新建隧道和既有隧道之间的距离是变化的,取新建隧道掘进至与既有隧道最近处,爆破施工时所测爆破振动如表2 所示。两隧道净距最近处为18.15m,隧道施工仅远离既有隧道侧采用爆破开挖,爆源中心与检测点的实际距离约为35m,其余监测点爆心距根据几何关系分别如表2 所示。
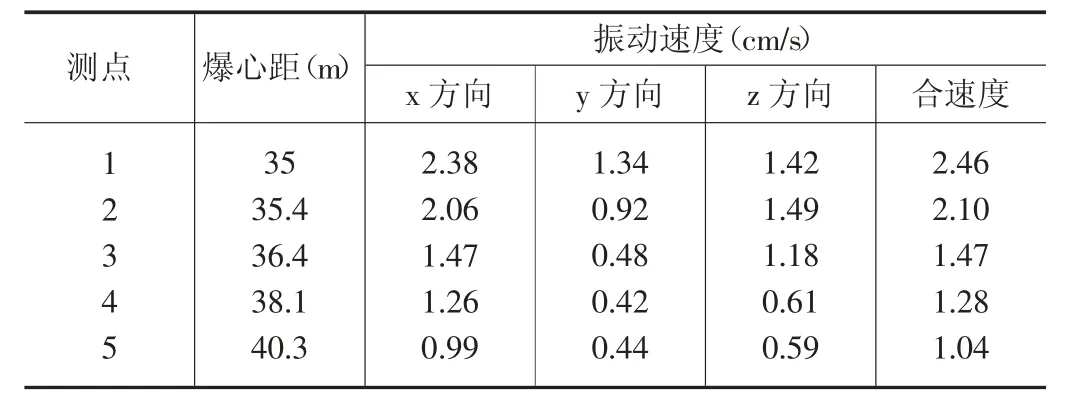
表2 爆破测振结果数据表
从表中所测数据可以得出,振速总体随着爆心距的增加呈减少趋势,从各个方向的分速度来看,垂直于隧道走向的水平方向振速最大(x 分量),垂直于隧道走向竖直方向振速次之(z 分量),沿隧道走向方向的水平方向振速最小(y 分量)。其中,测点1 实测合速度波形曲线如图4 所示。
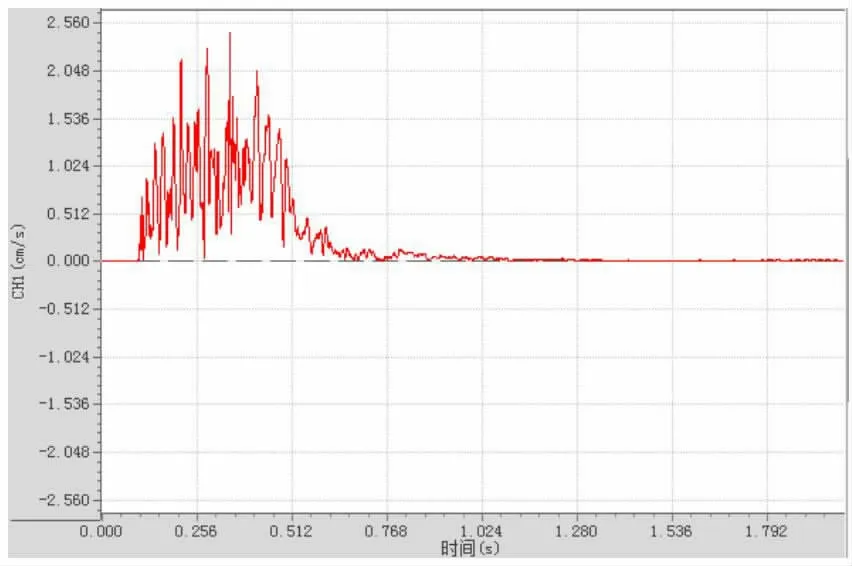
图4 测点1 合速度波形
3 数值模型建立和计算
以新建隧道现状为依据,建立1∶1 比例模型,考虑到和右线相比,新建隧道左线与既有隧道的距离更近,因此在研究时,以左线隧道的爆破施工为研究对象。由于隧道爆破断面布孔较多,为减少建模工作量,可将模型进行简化:将同段起爆的炮孔用一个等效炮孔替代,替换后的炮孔直径和炮孔位置采用以下方法确定:
将同一段起爆的药包简化为一个起爆药包,替换后的等效药包直径由式(1)计算[4]。
式中:D 为等效炮孔直径;n 为每一段的炮孔个数;d为实际炮孔直径;c 为常数,取0.621。
等效药包的位置采用理论力学合力矩确定[7],即根据隧道断面上各个炮孔的中心坐标,由式(2)求出所有炮孔的重心坐标,再用重心坐标建立等效几何模型。
根据以上理论可将爆破模型进行简化,实际施工中最大单段药量炮孔布置和简化后的模型示意图分别如图5所示。
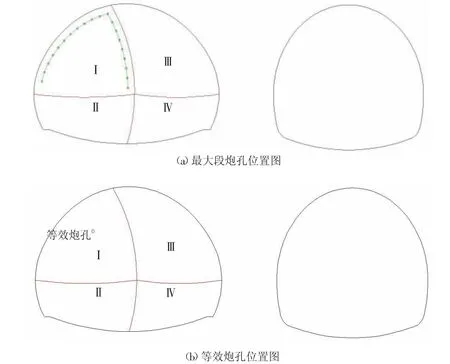
图5 炮孔简化示意图
根据简化后的模型,采用ANSYS/LS-DYNA 进行建模,单位制为kg-m-s。目前,应用ANSYS/LS-DYNA 进行爆破模拟,存在4 种主流的爆破荷载施加方法[8],其中采用荷载曲线模拟爆破荷载建模简单,求解速度快。荷载曲线采用国际主流的爆破荷载数值模型,其曲线表达式如式(3)[9]:
其中,P0为峰值应力,根据式(1)计算的等效炮孔直径取100mm,峰值应力参考文献[10],取P0=4500MPa;t 为自变量;t0为加载时间,取,α、β为常数,且β/α=1.5。加载曲线如图6 所示。
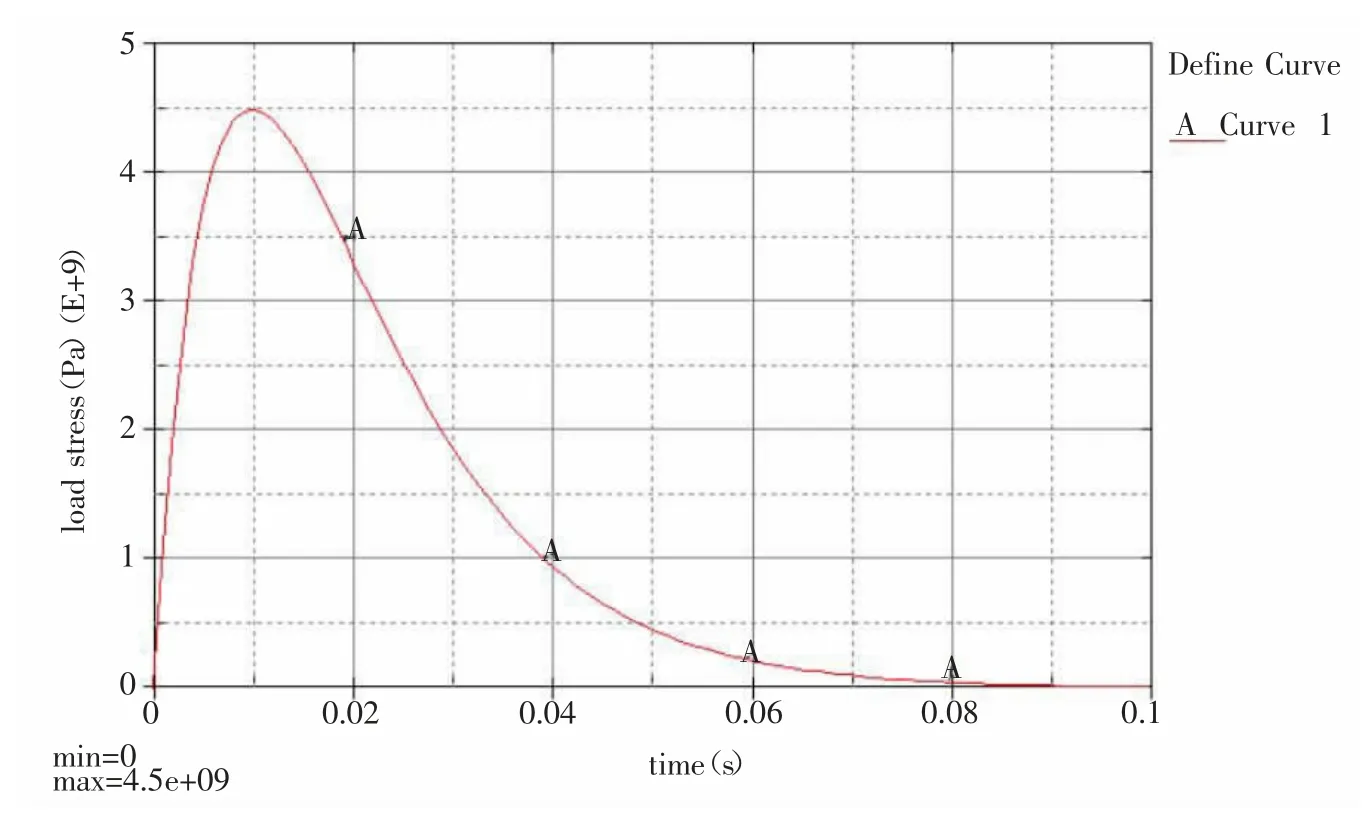
图6 爆破荷载加载时程曲线
既有隧道与新建隧道之间的岩体用关键字*MAT_JOHNSON_HOLMQUIST_CONCRETE 进行描述。为模拟炸药在无限介质中的爆炸,对除炮孔自由面以外的其他模型表面施加无反射边界条件,建模效果如图7 所示。
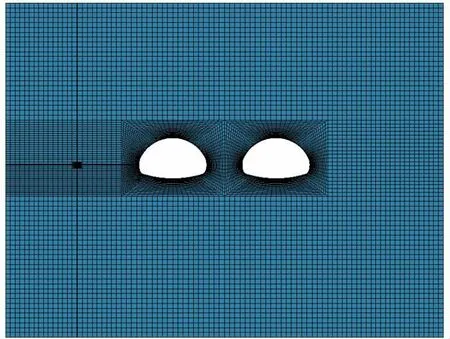
图7 建模效果图
4 模拟结果
分析计算结果时,在既有隧道左洞迎爆源一侧墙脚处与掘进掌子面齐平位置,沿掘进方向每隔5m 设置1 个监测点,共设置5 个,以监测相应位置在爆破作用下的振动速度。
在ls-prepost 中提取计算后各监测点的x、y、z 方向的振动速度(矢量)以及合速度(标量)情况,振动波形图如图8 所示。
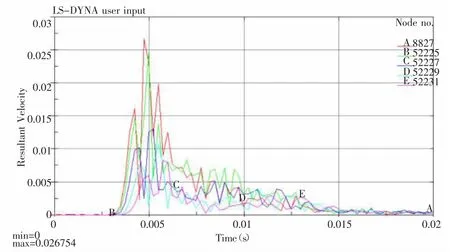
图8 各监测点振动波形图
从模拟结果来看,各个方向的振动速度随着爆心距的增加呈减小趋势。其中x 方向(垂直于隧道走向水平方向)振动速度最大,y 方向(垂直于隧道走向竖直方向)次之,z方向(平行于隧道走向水平方向)最小;各个监测点合速度的测振结果和模拟结果如表3 所示。
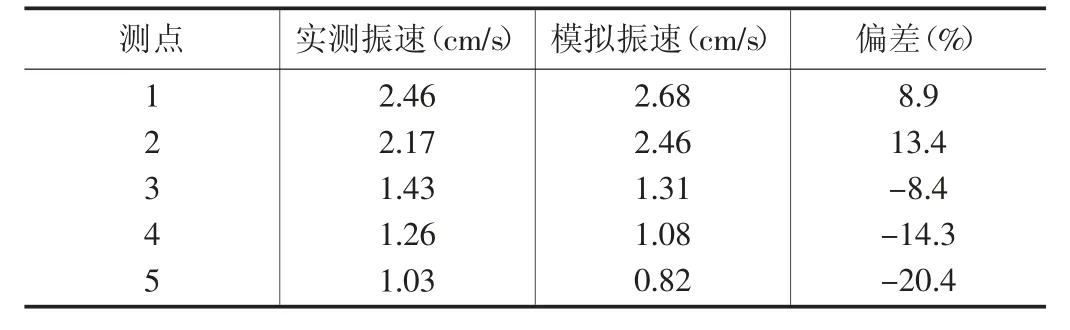
表3 实测和模拟振速对比表
从表3 中数据可以看出,数值模拟与实测结果吻合度较高,除测点5 外,其余测点的偏差均不超过15%,模拟的可信度较高。
5 安全性分析
对于既有隧道爆破振动控制标准,不同文件给出的标准值有着较大的差异。《爆破安全规程》中对既有交通隧洞的爆破振动安全允许标准最低为10cm/s;《铁路工程爆破振动安全技术规程》对隧道爆破振动安全允许值最低为5cm/s;袁良远等在研究中给出国内净距小于30m 的类似隧道爆破振动控制的标准值[11],其控制标准值根据隧道净距和建成年份的不同分别为5-10cm/s 不等,其中建成年份较久的隧道(建成于20 世纪70 年代),净距为20m 时,振动控制标准为6.0cm/s。考虑到既有隧道的现状,该爆破工程中既有隧道的爆破振动安全允许值确定为6cm/s。
由于评价爆破振动有害效应时以相互垂直的三个振动分量中的最大值和其对应的频率为评价指标。从测量结果来看,爆破振动速度最大的分量为垂直隧道走向的水平方向(x 轴方向),最大值为2.38cm/s,爆破振动波的频率一般集中在10~50Hz 区间。从模拟结果来看,在爆破最大单段药量为24kg 时,爆破振动对既有隧道的影响在安全允许范围内。
6 结论
①从各个方向的振动速度来看,垂直于隧道走向的水平方向振速最大,竖直方向次之,沿隧道走向的水平方向振动速度最小。②与既有隧道净距为18.15~25.48m时,在紧邻隧道一侧采用机械开挖,远离一侧采用爆破开挖,最大单响药量24kg的情况下,爆破作业产生的振动对既有隧道的影响在允许的标准以内,爆破作业安全。③用合力矩理论将多炮孔简化为一个等效炮孔,使用等效炮孔在ANSYS/LSDYNA 中建模研究爆破振动,该方法与实测数据对比,总体吻合度较高,较为可靠。

