奖惩机制下的闭环供应链决策与协调研究

黄彦丽 HUANG Yan-li；米力阳 MI Li-yang

（宁夏理工学院理学与化学工程学院，石嘴山 753000）

0 引言

近年来，为缓解资源短缺，减轻环境承载压力，回收再制造逐渐成为发展循环经济、绿色经济的重要组成部分，越来越多的供应链企业开始实施闭环供应链运营管理，国内外学者也从不同的角度对闭环供应链进行了卓有成效的研究，如Ma 等[1]在考虑政府补贴策略下研究双渠道闭环供应链定价决策问题，黄彦丽等[2]从纵向持股的角度探讨了回收再制造供应链的决策与协调，研究表明投资持股有助于提高废旧产品回收率和实现供应链帕累托改进。

针对供应链“双重边际效应”问题，国内外学者以供应链系统利润最大化为原则设计协调契约，如成本分担契约、收益共享契约和两部定价契约等，有学者将讨价还价的思想引入供应链的协调当中，如陈金龙等[3]在信息不对称下，运用Rubinstein 轮流出价博弈思想研究了第三方金融服务商与银行、企业之间利率定价问题。尽管讨价还价思想被广泛运用于实际问题的议价当中，但通过Rubinstein 轮流出价研究供应链协调问题的文献还相对较少。

基于此，本文在考虑奖惩机制下，针对单个制造商和单个零售商组成的回收再制造供应链决策与协调问题，分别构建分散决策和集中决策模型，并运用讨价还价的思想，设计Rubinstein 轮流出价协调策略，探析回收奖惩机制和贴现因子对供应链决策的影响，为供应链企业谈判和议价提供理论指导。

1 问题描述与基本假设

考虑由单个供应商和单个制造商组成的闭环供应链，供应商一方面用原材料生产零部件，另一方面通过设立回收站对废旧产品回收处理后作为原材料再利用。下游制造商采购此零部件用于生产终端产品。研究的具体假设如下：

①假设市场需求是线性的，即q=ξ-αp+e，式中ξ 为市场潜在需求量，α 为价格敏感系数，p 为零售价格，e 表示协同创新促使产品性能提升所带来的市场需求量的增加量。考虑协同创新固定投入为M＝e2/2，则供应商的创新投入为Cs（e）=λe2/2，制造商的创新投入为Cm（e）=（1-λ）e2/2，这里下标s 代表供应商，m 代表制造商，λ 表示供应商在协同创新中所承担的创新成本比例。

②供应商废旧产品回收成本由回收费用和回收材料处理成本两部分组成，用原材料生产零部件的单位成本为cs，用回收处理材料生产零部件的单位成本为cs0，废旧产品单位回收价为b，废旧产品回收率为θ，则回收费用为bθq[4]。回收材料处理成本主要包括废旧产品分解处理成本、人工成本，该部分成本为kθ2[5]，k 为回收规模参数。因此，废旧产品回收成本C（θ）=kθ2+bθq，其中k＞0，0＜θ＜1，cs-cs0-b＞0。

③除零部件的批发价w 外，制造商生产每件产成品的其他加工成本为cm，有p-w-cm＞0。

④为了鼓励废旧产品的回收再利用，政府执行废旧产品回收率奖惩干预政策，并设定了基准回收率θ0，当回收率大于θ0时，政府对供应商给予奖励，当回收率小于θ0时，政府对供应商的消极回收进行惩罚，则供应商的总奖惩额度为φ（θ-θ0），其中φ 为奖惩力度。

2 模型建立与均衡分析

2.1 分散决策模型（D）

在分散决策下，供应商和制造商的利润分别为

命题1：在分散决策下，当k＞kD时，闭环供应链决策均衡结果为：

供应商、制造商和供应链系统利润为：

结论1：回收率、需求量和制造商利润不受基准回收率的影响，但均与奖惩力度正相关。供应商利润与基准回收率和奖惩力度密切相关，当时，，当时，。

结论1 表明，奖惩机制有助于提高回收率，促进废旧产品循环再利用，从而提升环境效益，但作为废旧产品回收方，供应商利润与基准回收率负相关，与奖惩力度的相关性受基准回收率的影响。因此，基准回收率和奖惩力度的设置不仅要起到回收激励作用，同时还要保证供应商能从中受益。

2.2 集中决策模型（S）

在集中决策过程中，供应商和制造商通过合作共同决策，相当于一个整体，追求供应链整体利润最大化，于是供应链整体利润为

由于kS＞kD，所以在k＞kS时，有由此对比分散决策与集中决策下的均衡结果可得结论2。

结论2：当k＞kS时，有并且合理的回收率区间可设置为。

结论2 说明集中决策下废旧产品回收率、市场需求量以及供应链系统总利润更高，意味着集中决策的协同效应更为显著。显然，将基准回收率设置在两种决策下的回收率之间，这样不会使供应商失去完成回收目标的信心，而且有利于激发双方合作的意愿。

2.3 Rubinstein 轮流出价协调策略（R）

参考Rubinstein[6]无限期轮流出价博弈理论，将双方无限期讨价还价博弈转化为三阶段博弈，令τsi表示供应商在第i 个阶段所获得的溢出收益比例（i=1，2，3），令τmi表示制造商在第i 个阶段所获得的溢出收益比例（i=1，2，3），则，具体过程如图1 所示。

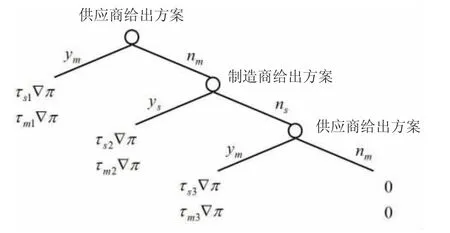
图1 供应商与制造商三阶段讨价还价博弈树

图1中，ym与nm分别表示制造商接受与拒绝供应商给出的分配方案，ys与ns分别表示供应商接受与拒绝制造商给出的分配方案，τsi和τmi分别表示博弈第i 阶段一方接受另一方给出的方案时各自分配的溢出收益。下面分析讨论具体的博弈过程。

第一阶段：供应商给出溢出收益分配方案（τs1，τm1），若制造商接受该方案，博弈结束，否则博弈进入第二阶段。

第二阶段：制造商给出溢出收益分配方案（τs2，τm2），若供应商接受该方案，博弈结束，否则博弈进入第三阶段。

第三阶段：由供应商第二次给出溢出收益分配方案（τs3，τm3），若制造商拒绝该方案，意味着双方均不能获得溢出收益，因此制造商一定会接受该方案。

根据逆向归纳法的思想，首先当博弈进入第三阶段，供应商给出的溢出收益分配方案为（τs3，τm3），然后考虑第二阶段，制造商给出分配方案（τs2，τm2），若使供应商接受，则供应商获得的溢出收益需高于第三阶段中分配的溢出收益，即τs2≥δsτs3，制造商出于自身利润最大化的目的，会给供应商分配最小的份额，于是τs2=δsτs3，由此第二阶段的最优溢出收益分配方案为（δsτs3，1-δsτs3）。最后考虑第一阶段，供应商给出分配方案（τs1，τm1），若使制造商接受，则制造商获得的溢出收益需高于第二阶段中分配的溢出收益，即τm1≥δm（1-δsτs3），供应商同样出于自身利润最大化的目的，会给制造商分配最小的份额，于是τml=δm（1-δsπs3），因此最优溢出收益分配方案为。

由于第三阶段与第一阶段是同一子博弈[6]，所以τs1=τs3，τm1=τm3，故有，求解可得子博弈精炼Nash 均衡解为：

命题3：在Rubinstein 轮流出价协调策略下，供应商、制造商的利润分别为：

结论3 表明，Rubinstein 轮流出价策略能够实现供应链协调，并且双方获取的利润与己方贴现因子正相关，与对方贴现因子负相关。另外，对任意δ∈（0，1），显然有，因而当双方贴现因子相当时，先给出方案的供应商能够获得更多的溢出收益，意味着供应商具有“先动优势”。 这就意味着在实际的讨价还价过程中，先出价的一方利用先动的优势尽可能使自身收益最大化，并且由于通货膨胀风险、潜在机会成本等因素会导致谈判成本增加，双方不可能具有多轮讨价还价的耐心，因而先动一方讨价还价的优势明显。然而，当双方的贴现因子均趋近于1 时，彼此有足够的耐心进行多轮甚至无限期谈判，此时先动优势几乎不存在，最终双方将平分溢出收益。

3 算例模拟分析

本节通过Matlab 进行数值模拟分析，进一步拓展本文结论，各参数取值为：ξ=300，α=5，e=18，cm=20，cs=12，cs0=6，b=4，k=115，λ=0.7。

取θ0=0.5，φ=30 时，贴现因子对双方利润的影响如图2、图3 所示。

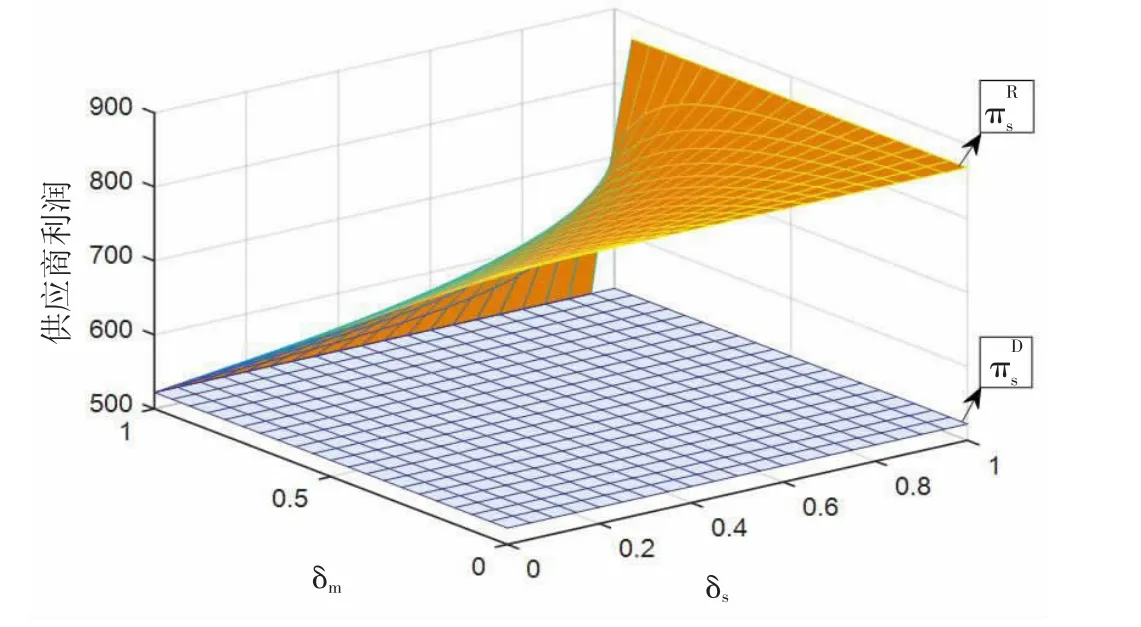
图2 贴现因子δs，δm 对供应商利润的影响

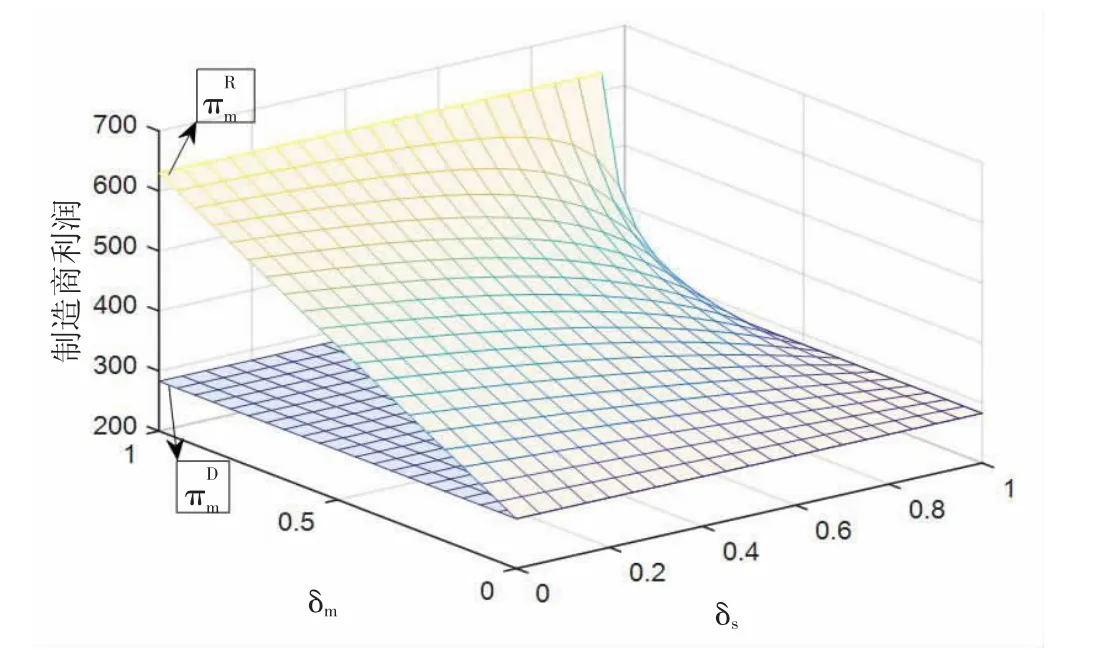
图3 贴现因子δs，δm 对制造商利润的影响

从图2、图3 可见，供应商和制造商利润均高于分散决策时的利润水平，表明Rubinstein 轮流出价协调策略能够实现供应链协调。另外，双方利润与自身贴现因子正相关，与对方贴现因子负相关，这就意味着参与者可以通过提高贴现因子建立谈判优势进而获得更多的利润。

4 结论

本文针对单个供应商和单个制造商组成的回收再制造供应链的决策与协调问题，运用讨价还价的思想，设计Rubinstein 轮流出价协调策略，探讨了回收奖惩机制和贴现因子对双方利润的影响，最后利用数值算例进一步验证和扩展了研究结论。研究表明：当奖惩力度在合理范围内时，奖惩机制对废旧产品回收再制造有正激励作用；Rubinstein 轮流出价协调策略能实现供应链完美协调，但双方获得的利润与自身贴现因子正相关，与对方贴现因子负相关。因此，参与者讨价还价的能力越强，在议价的过程中可以占据优势，就能获得较多的利润。