基于QNM-BP 神经网络边坡稳定性评价研究

向立 XIANG Li；王嘉弋 WANG Jia-yi；徐兴爱 XU Xing-ai

（云南磷化集团海口磷业有限公司，昆明 650000）

0 引言

边坡[1]是人类建设工程中开挖或填筑施工所形成的斜坡，随着工程建设范围的扩大，边坡稳定性成为工程中重要的安全问题。由于边坡失稳导致巨大损失的报道屡见不鲜，据不完全统计[2]，在2011 年至2020 年间我国边坡失稳致灾约7 万起，造成5000 余名人员伤亡，经济损失450 亿元左右。

边坡进行稳定性评价对失稳防治具有重要的现实意义。目前国内外的边坡稳定性评价方法主要有极限平衡法、极限分析法和有限元法。极限平衡方法[3]最先应用于边坡稳定分析中，该方法假定边坡破坏失稳时存在若干条潜在滑动面，把滑动面以上土体分割成若干土条，受力分析并简化假设得出平衡方程，进而评价边坡的稳定性；极限分析法[4]是对假定的滑裂面进行斜条分，建立协调的速度场，根据利用内能消散等于外力做功求解边坡稳定性系数，评价边坡的稳定性；有限元法是一种数值分析方法，分为有限元强度折减法[5]与有限元极限平衡法[6]，该方法通过计算机进行数值模拟评价边坡的稳定性。这些方法做了很多贡献，但边坡稳定性评价普遍存在有不连续、非线性和很多不确定性等实际因素，这类方法在评价时主观性较强，难以进行精准评价。近些年来，依托于数据的机器学习方法被引入到边坡稳定性评价中[7-9]，这类方法客观性强、计算迅速、工程中应用简单。

BP（Back Propagation）神经网络[10]是一种经典的机器学习方法，常用于评价问题。拟牛顿法（Quasi-Newton Method，QNM）是非线性问题的高效优化方法，本文采用QNM 算法优化BP 神经网络模型，建立边坡稳定性评价的QNM-BP 神经网络模型进行研究，并将其应用于工程中检验，得到一种具有应用价值的边坡稳定性评价方法。

1 原理

BP 神经网络是地质灾害评价问题中的常用方法。相关边坡稳定性评价的BP 神经网络研究[11-15]对其介绍较为成熟，本节重点介绍拟牛顿法（QNM）的计算过程[16]。

给定初始点x0∈Rn和β∈（0，1），σ∈（0，1），h>0，r≥0，选取B0=I（单位矩阵），置k=0。 搜索方向dk见下式：

如果dk=0，则停。

计算αk=βmk 使得mk是满足下式的最小非负整数m：

令zk=xk+αkdk。如果||F（zk）||=0，则停。计算：

最后一步按BFGS 校正公式计算Bk+1：

其中，

重复搜索方向所在的部分。

2 模型应用

2.1 样本库收集与展示

边坡稳定性的评价是一个多因素非线性问题，影响边坡稳定性的指标众多，指标的选取需要考虑边坡自身的物理力学性质、用于分析的地应力场以及用于监测的边坡参数。本文选取容重（kN·m-3）、粘聚力（kPa）、内摩擦角（°）、边坡角（°）、边坡高度（m）和孔隙压力比6 个指标作为边坡稳定性的评价指标，将边坡的稳定性评价结果分为失稳与稳定，分别记为等级1 和2。通过查阅文献[17-19]，本文收集了77 组边坡实例数据，用于后续的建模与研究，部分样本展示于表1。

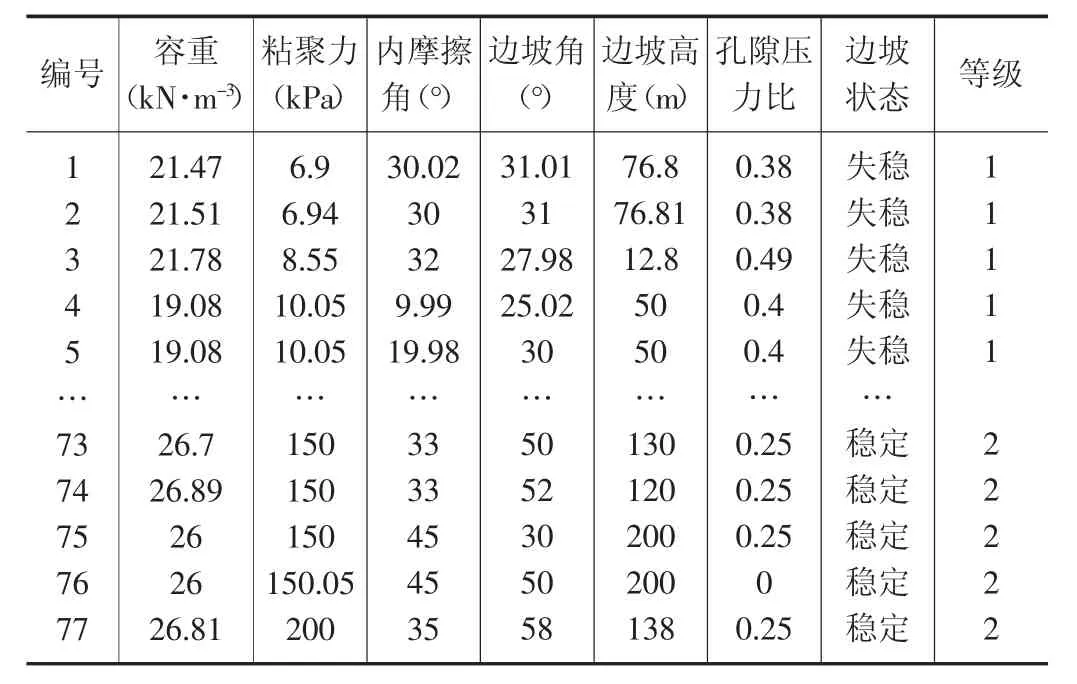
表1 部分边坡样本数据

2.2 模型搭建

BP 神经网络[12]分为输入层、隐含层和输出层，其中输入层为边坡稳定性评价指标，输出层为等级，隐含层设置为两层，网络结构见图1。样本库按7:3 切分为训练集与测试集，在MATLAB 平台上进行模型搭建，归一化采用MATLAB 自带的函数，建立QNM-BP 神经网络模型，并与传统的BP 神经网络模型进行对比研究。

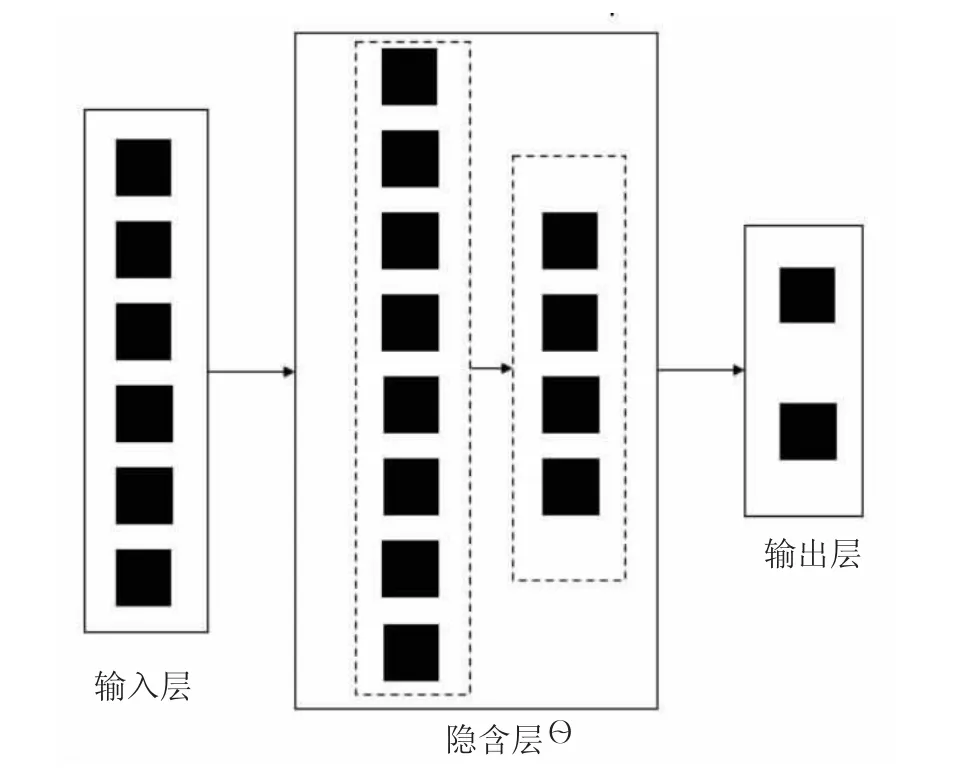
图1 BP 神经网络结构图

3 仿真与分析

3.1 评价结果展示

通过对样本库进行建模仿真，得到最终的评价结果，为了更好地了解本文所建的QNM-BP 神经网络模型的评价效果，对评价结果进行可视化，所有的评价结果以分类误差的形式展示于图2 和图3。

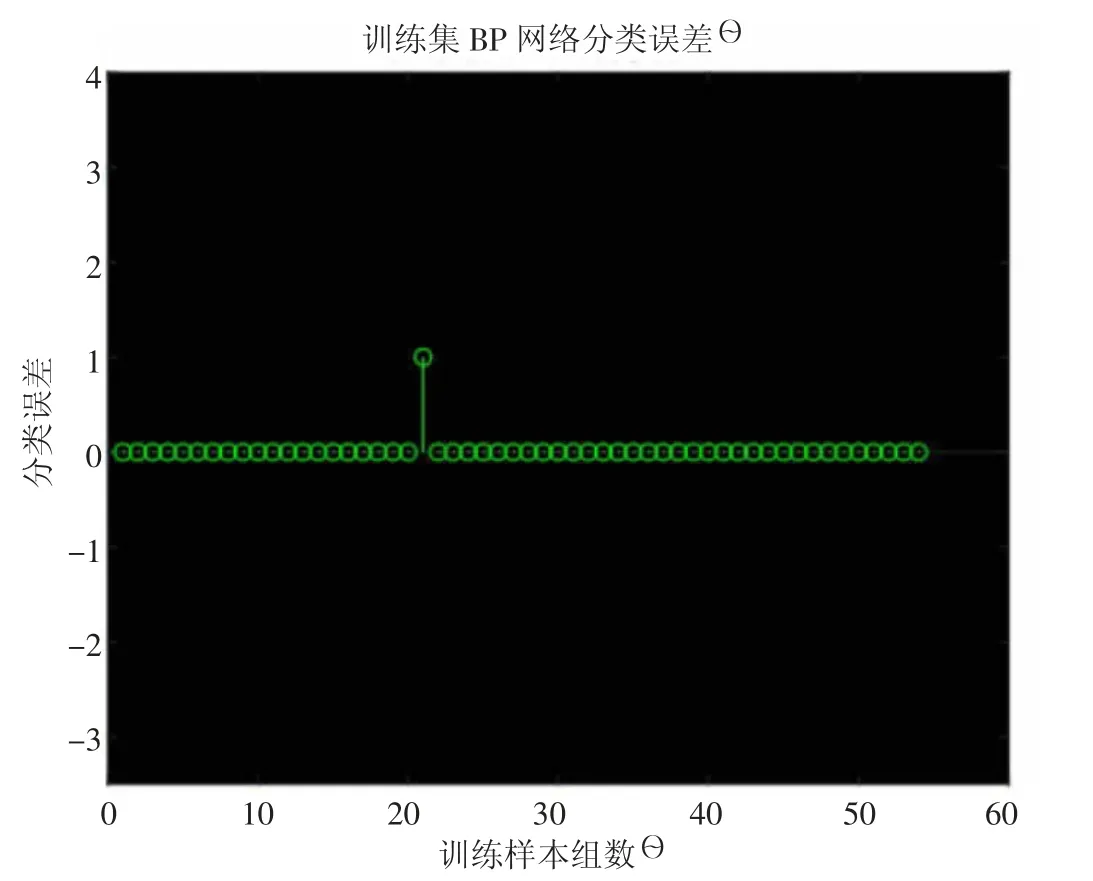
图2 QNM-BP 模型训练集分类误差

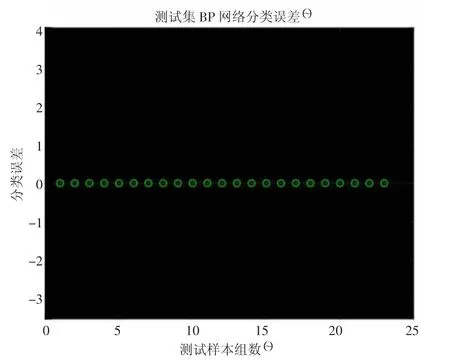
图3 QNM-BP 模型测试集分类误差

由图2 和图3 可知，本文所建边坡稳定性的QNM-BP模型对样本库的评价效果较好，训练集误判1 组案例，测试集的评价结果与实际情况一致，评价准确率达98.70%。

3.2 对比研究与分析

为了检验本文所选拟牛顿算法对边坡稳定性的BP神经网络模型的优化效果，采用同一样本库和相同参数设置建立一标准BP 神经网络模型，采用相同的评价结果展示方式，将评价结果展示于图4 和图5。

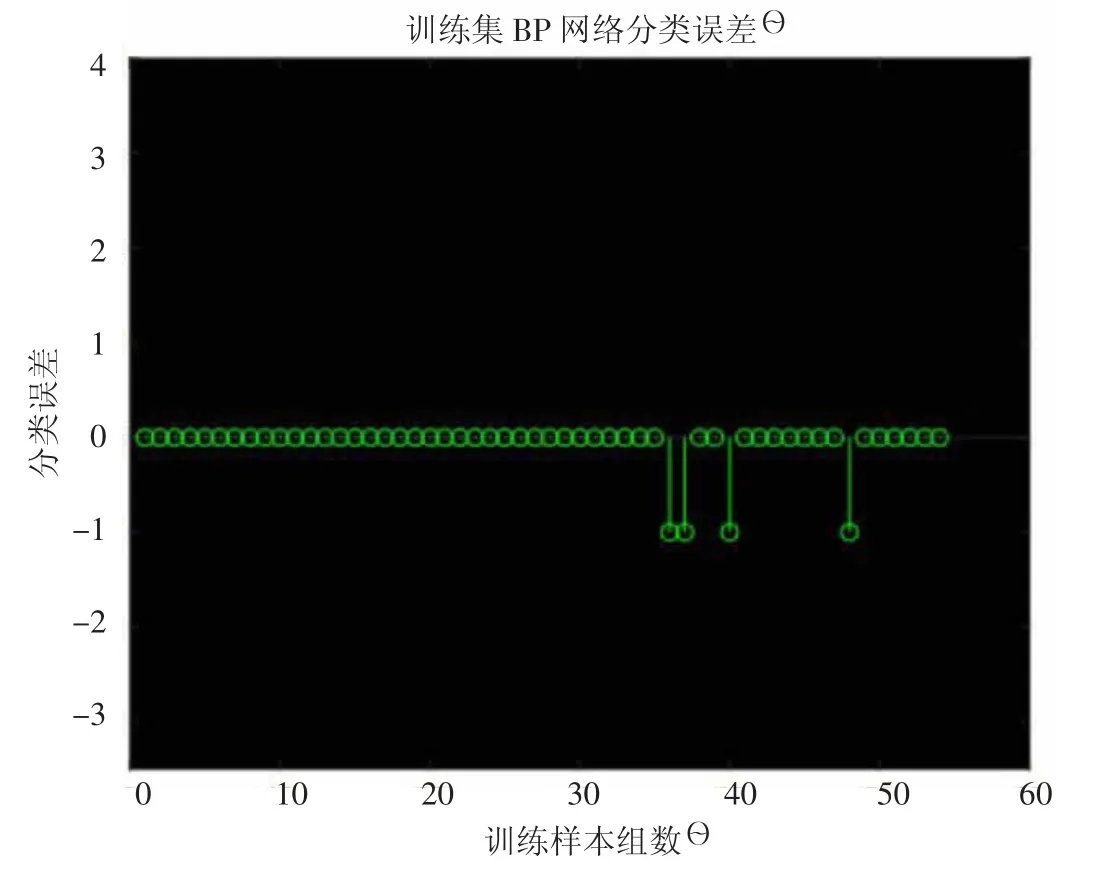
图4 标准BP 模型训练集分类误差

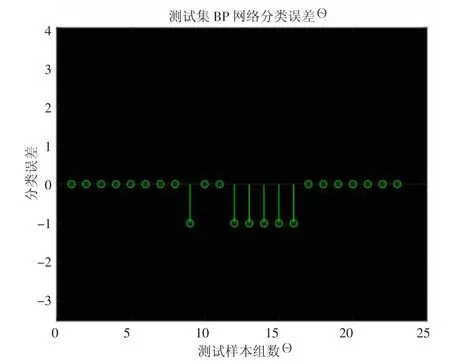
图5 标准BP 模型测试集分类误差

由图4 和图5 可知，标准BP 神经网络的边坡稳定性模型评价结果中，训练集误判4 个，测试集误判6 个，评价准确率为87.07%，远低于本文建立的QNM-BP 模型。

标准BP 神经网络采用梯度下降法进行训练，这种方法梯度的方向难以保证，在仿真的过程中易出现计算量大、迭代过程中易陷入局部最优，从而导致训练效果不佳；而本文选用的拟牛顿法使用负梯度和单独牛顿步寻优，简化了计算梯度，加快了执行速度，从而避免了陷入局部最优。

此外，模型的适用性上二者也有不同，本文选取的拟牛顿算法适用性更强，在非线性问题中表现更佳，这一点与边坡稳定性分析的非线性特征相契合，而不同模型的仿真结果也验证了这一点，本文所建的QNM-BP 神经网络模型评价更为精准。

4 工程应用

夏比公路[20]K85 段边坡位于藏北高原的比如县境内，以黑色板岩为主夹砂岩，石英岩夹火山岩，地层普遍受到了轻微变质。断裂构造以东西向为主，研究区新构造运动活动强烈，自中新世晚期以来新构造运动持续作用。边坡变形体的厚度在15-35m 之间，潜在变形方量约为140 万m3，K85 边坡物理力学参数见表2。

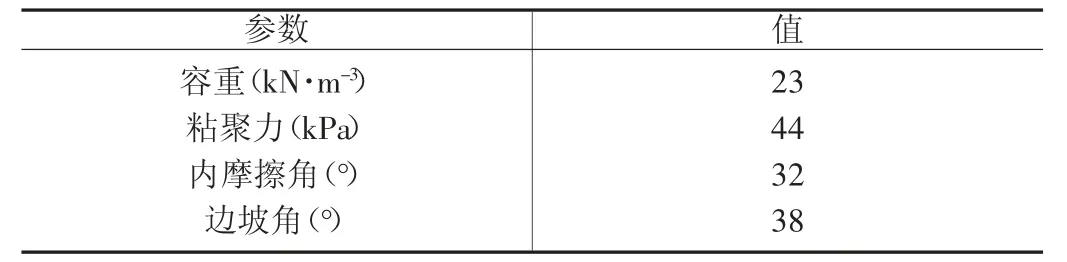
表2 K85 边坡物理力学参数值

将本文所建的QNM-BP 神经网络模型应用于夏比公路K85 段边坡中进行工程实例验证，评价结果见表3。由表3 可知，本文所建模型评价结果与实际情况一致，是一种工程实用性较强的边坡稳定性评价方法。

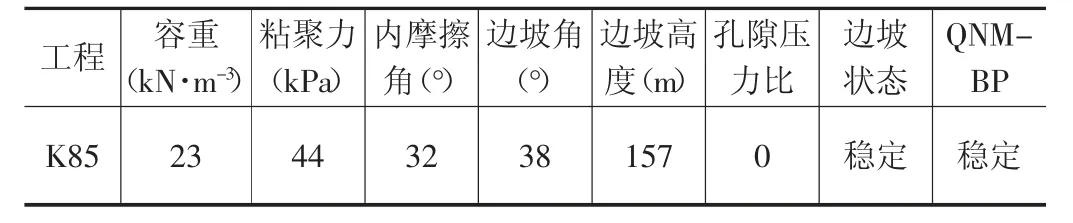
表3 K85 边坡稳定性检验表

5 结论

为了对边坡稳定性进行精准评价，本文引入QNM 算法优化BP 神经网络开展边坡稳定性评价研究，具体结论如下：①广泛查阅文献，建立了一个以容重（kN·m-3）、粘聚力（kPa）、内摩擦角（°）、边坡角（°）、边坡高度（m）和孔隙压力比为边坡稳定性的评价指标，边坡的稳定性情况为评价结果的实例样本库；②应用样本库数据建立边坡稳定性评价的QNM-BP 神经网络模型，模型评价准确率为98.70%，远高于标准BP 神经网络模型（87.07%）；③将建好的QNM-BP 神经网络模型应用于西藏夏比公路K85 段边坡进行检验，评价结果与实际情况一致，是一种精确有效的边坡稳定性评价模型。