声流对单管道周围换热特性的影响

李博轩，廉成龙，郭荣旺，祖梦泽，刘月超,2，姜根山

(1.华北电力大学数理系，河北保定 071003；2.华北电力大学河北省物理学与能源技术重点实验室，河北保定 071003；3.华北电力大学数理学院，北京 102206)

0 引 言

声学是一门学科交叉性很强的科学，声波可以影响物体的传热，对于炉内换热管，声波直接作用于换热管周围，能够使换热管传热强化，提高炉内换热管的传热效率[1]，因此研究声波对换热的影响有着重要的意义。迄今为止，国内外对于声波影响换热有不少的研究，其中何雅玲等对脉动流动强化散热进行了数值分析[2]，杨延锋等建立了声波作用下铜球的外声流特性模型[3]并开展了对声波强化传热实验研究与机理的分析[4]，许伟龙等[5]对铜球进行了声波换热实验，Ha等究了单液滴在振荡流下的燃烧情况[6]，除针对球状及颗粒物体的声波影响换热研究外，Molochnikov等研究了柱状物体的传热情况[7]，姜羽等对单圆柱声波下传热特性进行了数值分析[8]，杨延锋等对换热管外的声流特性进行了数值模拟[9-10]，Bahrani等[11]研究了振动圆柱诱导的稳定旋涡流动现象，Gopinath等[12]对强声场中圆柱的对流换热行为进行了实验研究。

综上，声波能影响物体的换热特性，而对物体的换热起到决定性的作用是声流[9-10]，声能量作用于物体表面的热黏性层，由于损耗形成的漩涡，即声流，通过漩涡的脱落与运动影响物体与介质的热交换情况。Nyborg等建立了声流的基本方程[13]，Lee等对声流进行了仿真研究，在研究声流过程中常采用了极限速度法[14]，Lei等将其优化并用于模型分析[15]。

本文类比炉内换热管，研究单根钢管的声波换热效应，通过不同声波下单管换热的强化因子，来比较不同声波对单管换热的影响。首先，采用COMSOL有限元分析软件进行数值仿真，用压力、速度描述和求解声场，运用频域接口，设定边界以求解亥姆霍兹(Hemlmholtz)方程，得到准确数值解后，导出声压或声压级的分布，以及切向速度的流线分布，与声流理论对比。然后，搭建单管道换热实验平台，设定不同的声压级和频率，监测管道温度的变化，研究声波对管道换热特性的影响并取得实验数据。结合仿真以研究实验现象的产生机理，即声波产生声流，声流直接作用于管道，从而影响管道的换热特性，为声波强化炉内换热管换热提供理论依据。

1 基本原理

1.1 声 流

声流运动属于黏性流体运动，由连续性方程和Navier-Stokes动量方程[15-16]控制：

式中：ρ为流体密度；t为时间；u为流体速度；p为压力；μ为动力黏度系数；μb为切变黏性系数。

根据微扰理论[17-18]，ρ、p以及u的表达式为

为研究声流场，采用极限速度法预测边界流场，建立一个柱状模型并截取xOy二维平面，示意图如图1所示。

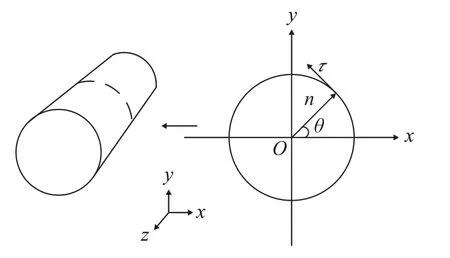
图1 柱状管道及其二维平面示意图Fig.1 Schematic diagram of columar tube and its two-dimensional plane

图1中，左侧为柱状模型，右侧为沿平行xOy平面截取柱状模型的二维平面，逆时针方向为τ的方向，n指向半径向外的方向。

θ在xoy平面中表示为

图1中，τ和n在xoy平面中可以表示为

极限速度取自二维平面的两个切向分量的极限速度，当半径远大于边界层厚度δ时有效[13]，实验中半径R远大于边界层厚度δ，δ的计算公式为

式中：ω为声波的角频率，ω=2πf0，一般在温度20 ℃、大气压强为101.325 kPa的空气中，声波频率为100 Hz，黏性边界层为0.22 mm，则频率为f0时，δ=0.22×10-3×(100f0)1/2。

Lee等根据式(1)中的方程[14]，求得在xOy平面下，极限速度在x轴与y轴的分量方程为

式中：uL为x轴的极限速度分量；vL为y轴的极限速度分量；Re为取实部；u1、v1、w1分别对应x、y、z轴的一阶声流速度分量；u*1以及v*1为u1、v1的复共轭。

v1τ和w1n在定点上的切向与法向一阶声流速度可表示为

式中：下标τ、n为相应方向的分量。

在二维平面下，圆柱外部声流的极限速度只存在切向分量，即：

联立式(6)、(7)中的方程可得到极限速度在圆形管道边界层的分布，便可通过极限速度分布表征声流流场的分布。

1.2 导热微分方程

在柱坐标系下，一维非稳态、无热源的导热微分方程为[19]

式中：ρi为钢管的密度；C为钢管的比热容；λ为钢管的导热系数；r为测量位置与钢管中心的距离；T为钢管的温度；t为时间。已知ρi为7.85 kg·dm-3；比热容C为4.2×103J·kg-1·℃-1；空气的导热系数λf为0.023 W·m-1·℃-1。

相应方程的初始条件应为

式中：T(R,0)为初始时刻钢管表面任意点的温度；Ti为钢管的初始温度。

为求解式(9)，还应代入相应的边界条件：

式中：T(R,t)为t时刻钢管表面的温度；T∞为环境温度；h为钢管表面与环境的对流传热系数。

将初始条件与边界条件代入导热微分方程，可以解得：

通过对式(12)变换，可得：

式中：A为钢管横截面积；V为钢管体积。

由式(13)可得温度T与时间t的关系，将实验数据代入式(13)即可得出对流传热系数h。根据已知条件求解式(14)即可解得努塞尔数：

式中：λf为流体媒质的导热系数；D为钢管直径。

定义强化因子为

式中：Nu为声波作用下的努塞尔数；Nu0为无声波作用下的努塞尔数。

努塞尔数表征钢管的换热效率，为了直观地对比声波对钢管的影响，将努塞尔数代入式(15)，以α表征声波对钢管换热的影响程度。

2 实验平台

图2(a)为实验平台示意图，在封闭腔体一侧开腔，并设置一个扬声器作为声源信号，采用声学软件VA-LAB4控制声波的参数，通过功率放大器连接喇叭(声源)，使声源能够产生声压级的范围为124～136 dB，频率范围为100～2 500 Hz的声波。声压传感器放置于钢管两侧，用于判断声压级大小，以靠近喇叭的一侧探头作为参考声压。测量温度时将热电偶置于钢管中，使热电偶前端贴于管壁上，将热电偶与温度传感器连接，由温度传感器记录数据。通过设定每组的参数(频率、声压级)，分别研究不同声学参数对换热的影响。

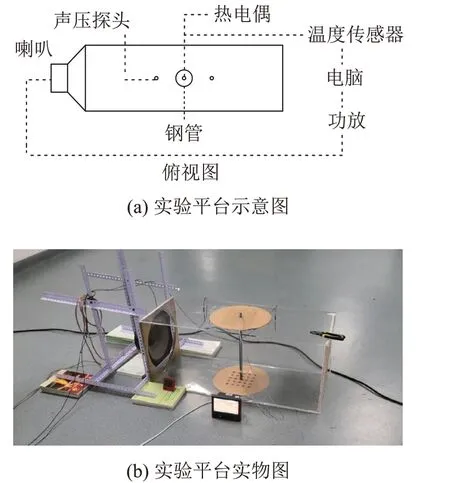
图2 实验平台示意图和实物图Fig.2 Schematic diagram and photo of experimental platform

图2(b)为实验平台实物图，钢管半径为1 cm，腔体长为1.15 m，宽为0.46 m，高为0.46 m，腔体左侧放置为声源，钢管由两块圆形板固定，钢管一头用于放置热电偶，在钢管两侧放置声压级探头，除此之外整体封闭，因此钢管可以近似认为只受声波的影响，腔体正面的显示器即为温度传感器，用以记录温度数据。

3 数值仿真

基于有限元软件COMSOL研究不同频率下的声压级分布情况以及声流分布情况。

3.1 几何模型

仿真模型如图3所示，虚线框表示计算域，D为钢管直径。对照实验平台的换热钢管，钢管直径为2 cm，计算域长为1.15 m，宽为0.46 m，左侧边界设定为压力或速度输入，其余边界为硬壁边界。

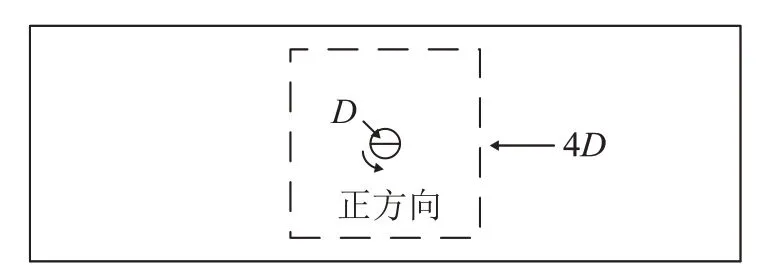
图3 计算声流特性仿真模型Fig.3 Simulation model for calculating acoustic flow characteristics

为得到更加精细的流速分布，将虚线部分设置为局部计算域。整体的网格剖分形式采用物理场控制的极细化类型，并规定速度沿图3圆形旁箭头所指方向为正，建立管壁处的切向速度线图，以研究管壁边界处的速度分布情况。

3.2 计算方法

当柱体的表面曲率半径远大于声学黏性边界层的厚度时，边界层内流涡末端的极限流速可以近似为声边界层外一阶线性声速场的函数，此时对物体周围流场起主要作用的是边界层外的声流，边界层内的声流作为边界层外声流的驱动力，可近似等效为物体表面的一个滑移速度。滑移速度的计算步骤如下：

(1) 选用有限元软件求解方程(3)用于计算一阶声场。计算模型参照图3，左侧边界采用速度激励，其余边界为硬壁边界条件。

(2) 利用流体层流模块求解二阶流场。将柱体的硬壁边界设定为滑移速度边界，滑移速度为通过步骤(1)得到滑移速度vL，其计算公式如式(8)所示。其余边界可设置为硬壁边界。

3.3 仿真结果

声压级的计算公式为

其中：Pref为基准参考声压，空气中取2×10-5Pa，实验中采用的声压级Lsp为130 dB，得到输入压力Pe，进行数值仿真。

管壁上声压级的分布情况如图4所示。由图4可知，频率1 300、1 900 Hz处的声压级明显下降(靠近特征频率)，其余频率处的声压级均在126.99 dB附近上下浮动，说明总体上频率变化对声压级的影响不是特别明显。

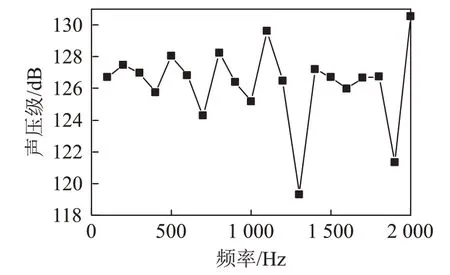
图4 管壁平均声压级随频率变化的仿真结果Fig.4 Simulation results of the variation of mean sound pressure level on tube wall with frequency

研究管道周围的声流分布，左侧边界设定为速度边界，声压级Lsp设为130 dB，计算频率为100、200、400、800 Hz时对应的切向速度分布以及管壁上的切向速度分布，最终得到不同频率下的切向速度分布图。质点振动速度与声压级的关系为

其中：ve为速度的有效振幅，vref=4.83×10-8m·s-1，为参考速度，声压级为130 dB时对应的速度激励ve=0.152 7 m·s-1。根据3.2节的计算方法，获得管道周围的声流切向速度分布，结果如图5所示。声流是声波的二阶非线性效应，其速度不等于声波的质点振动速度。

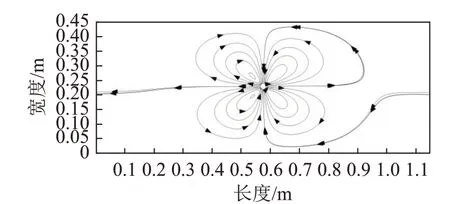
图5 频率为100 Hz的管道周围声流切向速度分布Fig.5 Tangential velocity distribution of acoustic streaming around the tube at the frequency of 100 Hz

以频率为100 Hz时的切向速度分布为全局流线分布的参考，观察图5可知，在声流的作用下，有4个紧贴中心圆形壁的对称涡旋结构，流动方向随位置发生周期性改变。声流效应中声能量通过作用于物体表面形成漩涡，由漩涡带走物体表面的热量以达到影响换热的效果。

图6为管壁上的速度分布图。观察图6可知，在100、200、400和800 Hz频率时，切向速度随位置的分布相似，即频率变化对速度分布的影响较小。图6(a)中，当频率为100 Hz时，最大切向速度达到5.85 mm·s-1，而频率为800 Hz时(图6(d))，最大切向速度仅有0.67 mm·s-1，即频率的变化对最大切向速度有较大影响，随着频率增大，最大切向速度减小。

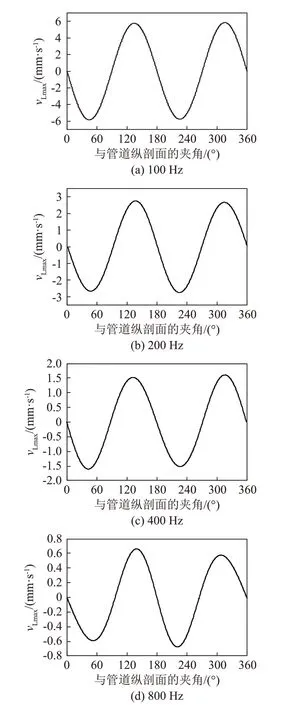
图6 不同频率时管壁上的速度分布Fig.6 Velocity profiles on tube wall at different frequencies

图7为不同频率对应的声流的局部切向速度分布图。由图7可知，不同频率下的涡旋结构无较大差异，即频率变化对声流结构无较大影响，而声波的频率增大，最大切向速度减小。

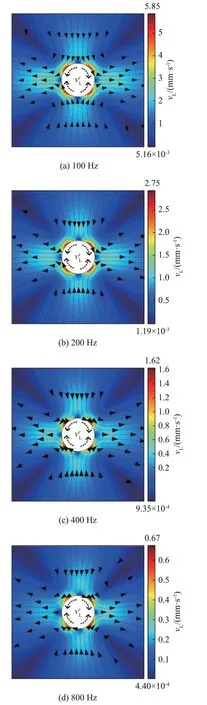
图7 不同频率对应的管道周围声流局部切向速度分布图Fig.7 Local tangential velocity distribution diagrams of acoustic streaming around the tube at different frequencies

Lee等给出声流边界层外部的最大流速与角频率有对应关系[14]：

式中：ω=2πf；f为声波的频率；R为圆柱的半径；ve对应输入的速度激励。仿真中所得最大速度与文献[14]的解析解对应关系如图8所示。

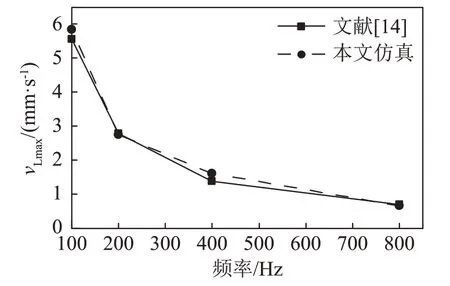
图8 切向最大速度与频率关系的仿真结果与文献[14]的解析解的对比Fig.8 Comparison between the simulated results of tangential maximum velocity versus frequency and the analytical solution in reference [14]

观察图8可知，本文的仿真曲线与文献[14]的理论曲线基本一致，即随着声频率的增大，最大切向速度减小。该结果表明了本文仿真结果的正确性。

4 实验结果与讨论

为研究声流大小对换热特性的影响，在实验中，将钢管加热至70℃左右，考虑温度分布情况，选取59℃～56℃的温度变化区间，设置两组实验。第一组实验控制频率不变，研究不同声压级对单管道换热的影响。第二组控制声压级不变，研究不同频率对单管道换热的影响。

第一组实验中，控制声波频率为100 Hz，对0、124、130和136 dB四种声压级进行研究(根据声压级与声压的换算，每增加6 dB，压力增加一倍，声压级为0 dB即不加声波下的情况)。图9给出温度从59℃下降至56℃过程中，不同声压级情况下钢管随时间变化的降温曲线，观察图9可知，声压级为130 dB和136 dB时钢管的降温速度明显大于对照组和124 dB时的降温速度，而对照组与低声压级的图线基本重合。

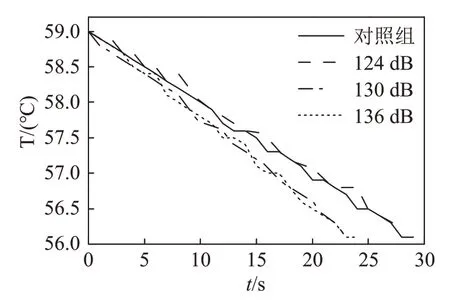
图9 不同声压级下温度随时间变化曲线Fig.9 Variation curves of temperature with time at different sound pressure levels

为更清晰地对比不同声压级对钢管换热效率的影响程度，将数据代入式(15)得到不同声压级下的强化因子α，结果如图10所示。图10中以声压级为0 dB时努塞尔数计算得到的强化因子的结果作为基准值1。观察图10可知，声压级在130 dB和136 dB的情况下，强化因子明显大于基准值1，在声压级为136 dB时，强化因子超出基准值近0.25，而声压级为124 dB时，强化因子为0.982，与基准值相差0.018，即没有太大变化，表明在相同频率下，高声压级的声波对钢管的换热增强效果影响较大，而低声压级的声波影响极小。

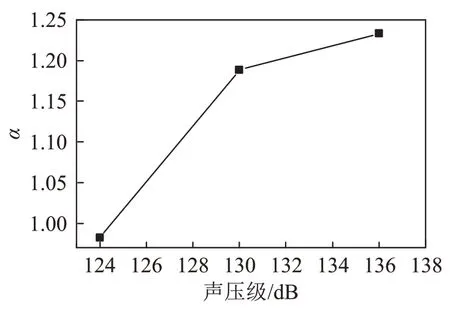
图10 不同声压级下的强化因子Fig.10 Enhancement factors at different sound pressure levels

式(18)中，最大切向速度与速度激励的平方成正比，而速度激励大小与声压级有关，声压级增大，对应的速度激励也增大。结合数值仿真中，切向速度的增加可以起到加强传热的效果，在实验中，增大声压级，即增大最大切向速度，能够加快钢管的换热速率。

在第二组实验中，控制入射声波的声压级为130 dB，声波的频率为100～2 500 Hz，得到强化因子随频率的变化，结果如图11所示。观察图11可知，总体上随着频率的增大，强化因子呈现下降趋势，频率不断增大，强化因子下降的幅度减小。在频率100 Hz声波的作用下，强化因子达到最大，200～600 Hz声波下的强化因子大幅减小，此后强化因子下降的趋势减缓。可见，在130 dB下，低频率声波对钢管换热的影响增强，而随着频率升高，强化因子减小，对钢管换热的影响减弱。

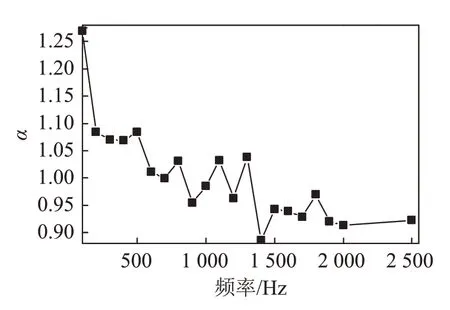
图11 强化因子随频率的变化Fig.11 The variation of enhancement factor with frequency

由仿真结果与理论分析可知，声流作用于物体表面，直接影响物体的换热，声波频率增大时，声流的切向速度减小，涡旋从表面带走热量的速率降低，使得物体降温速度减慢，在实验中表现为钢管的换热速率下降。

5 结 论

本文采用数值仿真和实验相结合的方法，开展管道周围声流对其换热特性的影响研究。由数值仿真和实验结果可知，声波直接作用于物体表面形成声流，其涡流能够带走物体表面的热量，达到加快物体换热的效果。研究表明，声流切向速度越大，涡旋带走物体表面热量的效果越好，而声流的最大切向速度与声波的频率和声压级直接相关，低频率高声压级的声波能够加强单管道的换热效率。

因此，增大声压级或降低频率，可以使声流的最大切向速度增大，从而提高物体的换热效率。管道周围声流对换热特性影响的研究，能够为声波强化炉内换热管换热提供理论依据。