大粗糙度起伏下一维海面声散射建模与分析

周 江，王 斌，王文欢，范 军

(1.上海交通大学，上海 200240；2.海洋智能装备与系统教育部重点实验室，上海 200240)

0 引 言

起伏海面的声散射特性研究在水声通信、主动声呐探测和水声对抗等领域有着广泛的应用[1-5]。对于中远距离的声场传播问题，大入射角甚至掠入射条件下的起伏海面声散射特性一直是研究的重点之一。然而，对于水面目标或水面附近目标如水面舰船、水下航行器等的声呐探测和预警问题，考虑到海面与目标之间复杂的相互作用，需要对起伏海面的声散射进行建模与分析，尤其是小入射角下大粗糙度起伏海面的多次声散射不容忽视。近年来国内外对粗糙海面的声散射发展了多种精确和近似的解析方法，主要有：可以近似计算绝对软边界条件下粗糙海面散射声场的积分方程法[6-7]，其优点是考虑了多次散射和影区的贡献，但因其计算量较大无法应用于工程中；当随机起伏方差和相关长度远小于入射波波长时，适用于低频近似条件的小尺度起伏粗糙面的微扰法[8-10]；当粗糙面平均曲率半径远大于入射波波长、随机起伏方差和相关长度远大于入射波波长时，适用于高频近似条件下的大尺度起伏粗糙面的基尔霍夫近似(Kirchhoff Approximation,KA)方法[11-15]等，其优点是形式简单，但是不能计算小入射角下大粗糙度起伏海面的多次声散射；可以近似计算均方根斜率较小的粗糙面散射声场的小斜率近似法[16-17]。随着计算机技术的快速发展，一系列数值计算方法如有限元方法[18]、边界元方法[19]等也可用于起伏海面声散射计算，但是由于网格划分工作量巨大，仅适用于低频计算。针对KA方法的缺点，研究人员也做出了相应的修正，比如Mc-Cammon等[20-21]利用修正的KA方法计算了绝对软边界条件下正弦表面的散射场，同时也考虑影区、多次散射和表面曲率的影响。Welton[22]将KA方法与菲涅尔(Fresnel)相位近似相结合，研究了几何影区、二阶散射和发射(接收)指向函数对绝对软边界条件下正弦表面散射声场的影响。尽管文献[20-22]已经将海面多次散射引入到KA方法中，但其应用局限于确定性正弦海面声散射情况。Richards等[23]将KA方法与射线理论相结合，根据本征声线计算海面散射声场，但是该方法不适用于焦散区和声影区，难以计算大粗糙度起伏海面的多次散射声场。

本文在传统KA方法的基础上考虑了海面的阴影区和亮区之间的多次散射，推导了大粗糙度起伏海面多次声散射的迭代求解公式，从而提出了一种适用于起伏海面高频散射声场计算的改进KA方法。该方法拓宽了传统KA方法的适用范围，对海面的形式、均方根斜率和起伏高度以及声波的入射角度没有限制。本文以一维余弦和高斯谱海面的有限元结果为标准解，验证了本文方法的准确性和适用性。以一维余弦海面为例，本文分析了不同入射声波频率和角度下海面散射强度的分布情况，并解释了Bragg散射的产生机理。以一维高斯谱海面为例，本文讨论了不同海面均方根高度和相关长度情况下高斯谱海面散射强度的变化规律。

1 改进的Kirchhoff近似方法

针对声波入射到一维起伏海面上的情形，本文采用了如图1所示的声散射模型，海面S起伏高度为z=η(x)，声波入射角和散射角分别为θi和θs，海面水平长度L取决于发射、接收指向性以及距离。利用改进的KA方法求解该模型的中高频散射声场，如图2所示该方法将其声散射分为两部分，(1)入射声波照射海面亮区的直接散射，忽略了海面影区对散射声场的贡献。(2)海面的多次声散射，考虑了海面亮区内某点处的第一次声散射对海面上其他点(包括亮区和影区)的作用，从而引起第二次声散射，同样也引起了其他高阶散射。

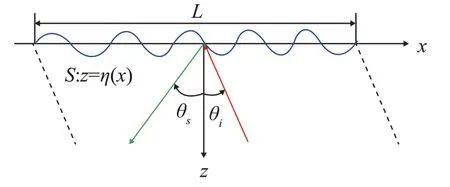
图1 起伏海面声散射几何模型Fig.1 Geometric model of acoustic scattering from undulating sea surface

图2 起伏海面多次声散射机理Fig.2 The mechanism of multiple acoustic scattering from the undulating sea surface

根据惠更斯第二积分公式[24]，可得满足自由边界条件的起伏海面散射声压(略去时间因子e-iωt)为

式中：是单位表面法向量，r2是接收点的位置矢径，rs是起伏海面的位置矢径。为了简化书写形式，将向量表示为rα-rβ≜Rαβ，其模|rα-rβ|≜Rαβ，单位向量RαβRαβ≜，下角标α和β对应不同的位置矢径。格林函数及其法向量可表示为

式中：cosθs=·(rs)，H0(1)和H1(1)分别为第一类零阶和一阶汉克尔函数。文献[25]也指出，海面散射相当于一系列偶极子声源的辐射，此时ptot(rs)是该等效偶极子模型的总声源密度[25]，于是有：

式中：pq，q=1，2，…表示第q阶偶极子声源密度，式(3)可以通过迭代方法进行求解。

考虑到海面的第一次声散射是由入射声波激励的，且海面表面满足自由边界条件，根据Kirchhoff近似可得

式中：入射声压pinc(rs)=H0(1)(kR1s)，r1是发射点矢径；可见性函数γ1(R1s)定义为

考虑海面的第二次声散射，此时海面上再辐射声源是由第一阶偶极子声源激发的，于是有：

式中：rs，r's∈S分别为场点和源点，cosθs'=·(rs')；互可见性函数γ2(Rss')定义为

依次类推，该等效模型的第q(q≥2)阶偶极子声源密度可归纳为

为了对式(1)中的积分进行数值求解，将总长度为L的海面离散成N个单元，则该起伏海面的散射声场近似等于这N个单元各阶散射声场相干叠加之和。以如图3所示的线单元对为例，c(m)和c(n)是它们的几何中心点，其矢径分别为和，A(m)和A(n)是单元上任意点，其矢径分别为和。为了简化书写，将向量表示为其模单位向量上角标(m)和(n)分别对应第m和n个线单元(m≠n)。式(1)可以离散表示为

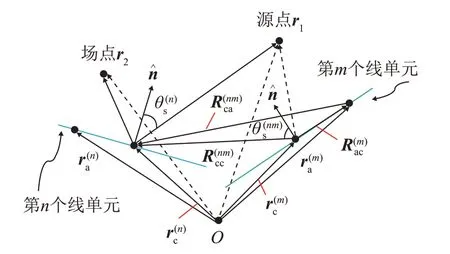
图3 线单元对等效偶极子模型Fig.3 Equivalent dipole models of line element pairs

第n个单元的第q(q≥2)阶偶极子声源密度为

此时，对于式(1)的求解就转化成对N个线单元的积分计算，而线单元的积分式可以进一步转化成与线单元坐标相关的求和解析式。利用一阶泰勒公式进行近似，可以得到：

于是有：

该迭代过程的终止条件为

式中：ε为收敛限定的最小正数阈值。得到起伏海面的单位长度散射强度为

在上述的推导过程中，考虑了海面的影区遮挡和多次声散射效应，故式(9)可应用于中高频率、大粗糙度起伏海面的单、双站声散射计算。而经典的物理声学方法通常假设几何影区对散射声场的贡献可以忽略，故只限于式(9)中q=1时的一阶散射声场计算，式(9)仅讨论了一维情况。将式(9)中二维格林函数改为三维格林函数，即可适用于二维海面的计算，从而更加符合工程实际应用情况。另外，下文中一维海面相关结论均可推广到二维情况。由于本文侧重点在于方法的提出和验证，以及海面一般规律总结，所以对于不同参数下任意形状二维海面的相关散射计算不再赘述。

2 方法验证

起伏海面可以看作是由无数个不同波长、波高和相位的谐波海面叠加形成的。基于两种不同类型的起伏海面模型对本文所提方法进行验证，对于规则的余弦波海面，其波面方程为

式中：-L2≤x≤L2，H、Λ和φ分别为波高、波长和相位。对于随机起伏海面，选择典型的高斯谱描述粗糙海面的结构和能量分布，其一维表达式为[11]

式中：δ为海面的均方根高度，决定了粗糙海面的起伏程度；l为相关长度，它决定了粗糙海面的横向变化频率。再利用蒙特卡洛(Monte Carlo)方法[26]，结合高斯谱进行一维海面几何建模。图4(a)给出了一维余弦海面高度曲线η(x)，其中H=0.4 m，Λ=1 m，φ=π，L=10 m。图4(b)给出了基于高斯谱生成的一维海面高度曲线η(x)，其中δ=0.4 m，l=1 m，L=10 m。

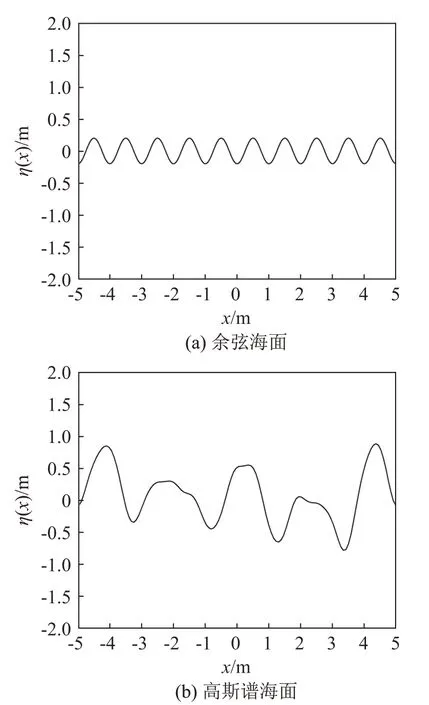
图4 一维余弦和高斯谱海面模型Fig.4 One-dimensional cosine and Gaussian sea surface models

下面分别利用改进的KA方法、KA方法和有限元方法计算如图4所示的两种一维海面模型的散射强度。图5比较了θi=10°和f=10 kHz时三种方法计算的散射强度随散射角变化结果，其中图5(a)为余弦海面模型，图5(b)为高斯谱海面模型。图6比较了θi=10°和θs=10°下的三种方法计算的海面镜向散射强度随频率变化结果，其中图6(a)为余弦海面模型，图6(b)为高斯谱海面模型。

图5 一维海面模型三种方法散射强度随散射角变化计算结果Fig.5 Variations of scattering intensity with scattering angle calculated by three different methods for the two one-dimensional sea surface models

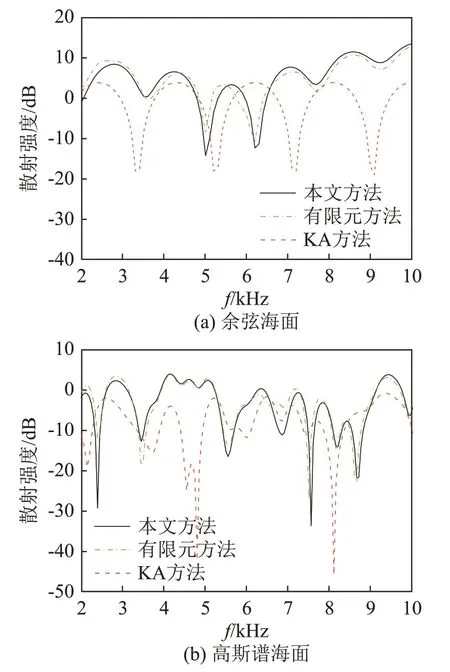
图6 一维海面模型三种方法散射强度随频率变化计算结果Fig.6 Variations of scattering intensity with frequency calculated by three different methods for the two one-dimensional sea surface models

由图5和图6可以看出，对于大倾角的余弦和大粗糙度的随机起伏海面，当入射角和散射角均较小时，传统KA方法的计算结果与有限元结果误差较大，且误差随着频率的增大呈增大趋势，而本文所提出的改进的KA方法很好地解决了传统KA方法存在的问题，其计算结果与有限元结果具有很好的一致性，这为改进的KA方法计算起伏海面声散射的准确性和适用性提供了理论依据。

3 计算结果与分析

3.1 不同入射波发射参数对余弦海面散射强度的影响

为了清晰描述不同参数对海面声散射特性的影响，在以下的计算中均利用改进的KA方法计算式(14)定义的一维余弦海面的分置散射强度。若无特殊说明，海面参数选取H=0.4 mm，Λ=1 m，L=10 m。

图7给出了f=10 kHz下四个典型声波入射角度下海面的总体、一阶和二阶的散射强度对比结果，图7(a)～7(e)分别为θi=0°，30°，45°和60°下的对比，图7(f)是上述4个典型入射角度下总体、一阶和二阶的散射强度的概率分布结果。

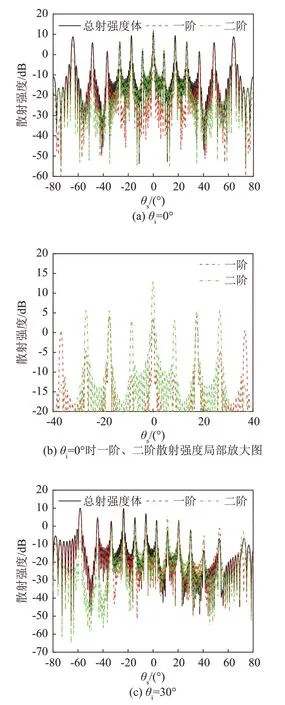
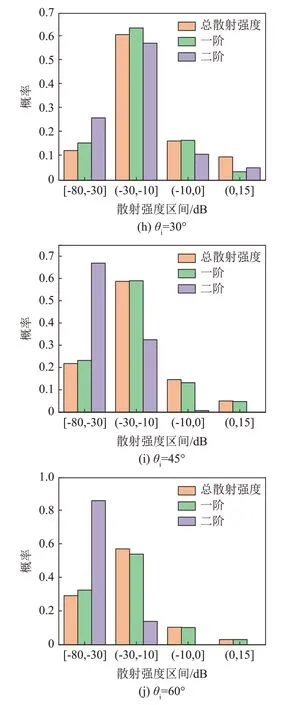
图7 不同入射角下余弦海面的一阶、二阶和总散射强度随散射角的变化及其概率分布Fig.7 Variations of the first order, second order and total scattering intensities with scattering angle and their probability distributions under cosine sea surface and different incidence angles

从图7(a)和7(c)可以看出，对该最大波倾角为72°的余弦海面，当入射角为0°或30°时，在部分散射角度下海面的二阶散射强度比一阶散射强度高出5～15 dB(在θi=0°时补充了放大图)，在散射强度[0，15]dB区间内海面的总散射强度概率要大于一阶散射强度概率，这说明海面的二次散射对总散射声场的贡献不可忽略；当入射角为45°和60°时，只有少数散射角度下海面的二阶散射起作用；而当入射角为60°时，在散射强度[0，15]dB区间内海面的二阶散射强度概率几乎为0，这说明海面的高阶散射贡献可以忽略。进一步分析图7可以看出，当入射角小于45°，且散射角|θs|小于45°时，余弦海面的二阶散射声场对总散射声场的贡献较大，而随着入射角和散射角|θs|的减小，二阶散射的影响是逐渐增大的。这说明在小入射角和小散射角条件下，海面的多次散射效应予以考虑，而且越接近垂直入射，海面的多次散射效应越明显。

为了更清晰地观察声波入射角度对散射强度的影响，图8进一步给出了f=10 kHz下海面散射强度的入射角度-散射角度谱图。图8(a)～8(c)分别对应总体、一阶和二阶的散射强度。图9给出了θi=0°时余弦海面散射强度的频率-散射角度分布图，图9(a)～9(c)分别对应总体、一阶和二阶的散射强度。

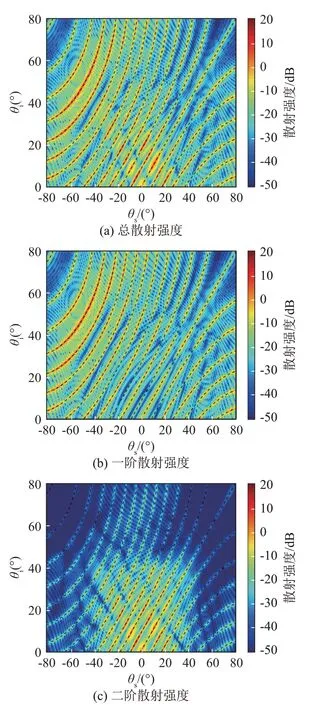
图8 余弦海面散射强度随入射角度和散射角度变化云图Fig.8 Variation nephograms of the first order, second order and total scattering intensities with incidence angle and scattering angle under cosine sea surface

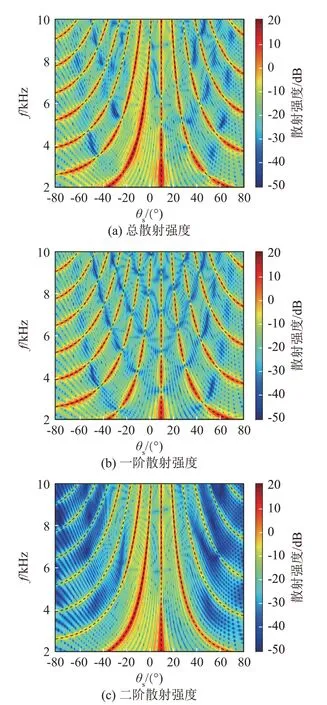
图9 余弦海面散射强度随频率和散射角度变化云图(θi=10°)Fig.9 Variation nephograms of the first order, second order and total scattering intensities with frequency and scattering angle under cosine sea surface and θi=10°

图8(b)和图9(b)中的亮线可以用Bragg散射来解释。Bragg散射的根本原因是海面波浪间散射回波的相干叠加。Bragg散射示意图如图10所示。α和β是相邻的两个波谷，入射声波通过点α的路径长度为A+D，通过点β的路径长度为D+E。只有通过两点α和β的声程差是声波波长λ的整数倍，即满足条件(D-E)-(B-A)=±nλ时，Bragg散射才会发生。根据几何关系：(D-E)=Λsinθs和(B-A)=Λsinθi，Bragg散射的条件[27-28]为

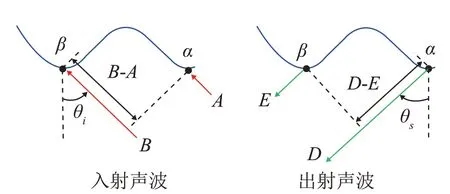
图10 Bragg散射示意图Fig.10 Schematic diagram of Bragg scattering

图8、9中黑色虚线均是根据式(16)画出的Bragg散射线。由图8(b)和图9(b)可以看出，黑色线的位置与亮线吻合得非常好，且亮线的数量随着频率的提高而增多。这说明在中高频段，当声波波长远小于海面波长时，Bragg散射对海面一阶散射声场的影响很大，而且随着频率的提高，Bragg散射效应更加明显。在图8(c)和图9(c)中，另一个发现是，海面的二阶声散射亮线和一阶声散射亮线出现在相同的位置。

3.2 不同海面参数对高斯谱海面散射强度的影响

3.2.1 不同均方根高度下的高斯谱海面散射强度

图11给出了不同波高下海面的散射强度随散射角变化结果，其中θi=10°和f=10 kHz。保持高斯谱海面相关长度不变，改变均方根高度δ=0.4和1.2。随着高斯谱海面均方根高度的增大，海面粗糙度增大，海面二阶散射对总散射声场的贡献越来越大。当声波以10°入射到均方根高度δ=1.2的高斯谱海面时，海面的多次散射无法忽略。在小入射角条件下，海面的均方根高度越大，海面的多次散射效应越明显。

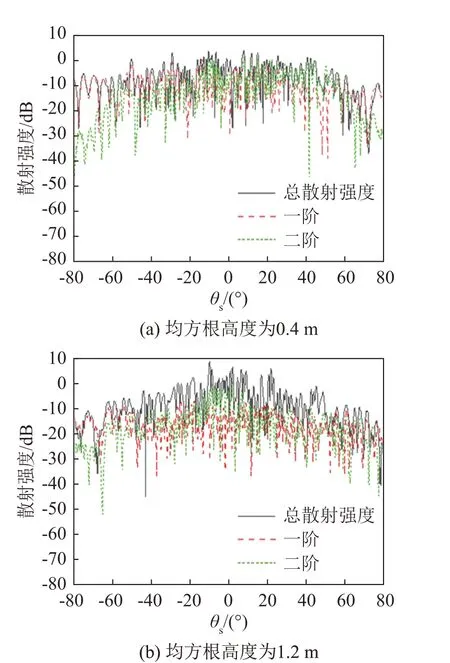
图11 不同海面均方根高度对高斯谱海面散射强度的影响Fig.11 Influence of different root mean square heights of sea surface on the scattering intensity from Gaussian sea surface

3.2.2 不同相关长度下的高斯谱海面散射强度

图12给出了不同波高下海面的散射强度随散射角变化结果，其中θi=10°和f=10 kHz。保持海面均方根高度不变，改变相关长度l分别为0.5和1.5。随着高斯谱海面相关长度的增大，海面二阶散射对总散射声场的贡献越来越小，海面的一阶散射对总散射声场起主要贡献。当声波以10°入射到相关长度l=1.5的高斯谱海面时，海面的多次散射可以忽略。在小入射角条件下，海面的相关长度越小，海面的多次散射效应越明显。

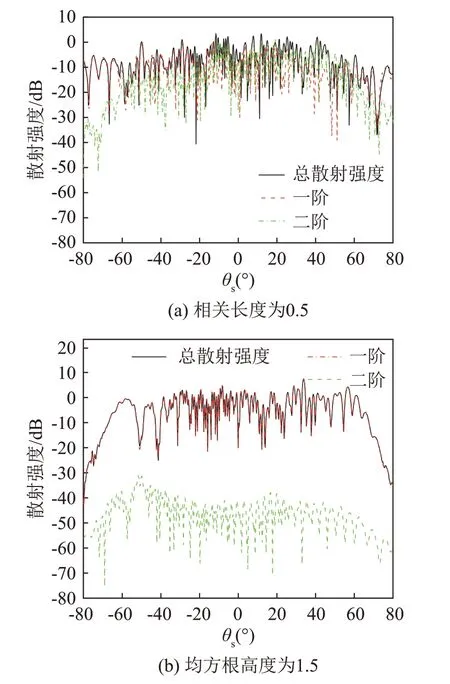
图12 不同海面相关长度对高斯谱海面散射强度的影响Fig.12 Influence of different correlation lengths of sea surface on the scattering intensity from Gaussian sea surface

4 结 论

本文针对起伏海面高频声散射计算问题，提出了一种改进的物理声学方法。与经典KA方法的不同之处在于，这种方法考虑了海面的阴影区和亮区之间的多次声散射，较大地提高了计算精度。本文以一维余弦和一维高斯谱海面为例，该方法与有限元方法计算结果的比较，表明该方法适应于中高频、小入射角下大倾角起伏海面的声散射计算。根据一维余弦海面散射强度的计算结果，分析了不同入射声波角度和频率对海面散射强度的影响规律，解释了Bragg散射的产生机理，同时讨论了不同海面均方根高度和相关长度情况下高斯谱海面散射强度的变化规律。结果表明：

(1) 在小入射角和小散射角条件下，均方根高度较大的高斯起伏海面的多次散射效应要予以考虑。随着入射角的减小和海面均方根高度的增大，海面的多次散射对总散射强度的贡献越来越大；

(2) 在小入射角和小散射角条件下，相关长度较小的高斯起伏海面的多次散射效应要予以考虑。随着入射角的减小和海面相关长度的减小，海面的多次散射对总散射强度的贡献越来越大；

(3) 当声波波长远小于余弦海面波长时，Bragg散射对海面声散射的影响较大。随着余弦海面波长的增大和声波频率的提高，Bragg散射条纹增多，海面的Bragg散射效应更加明显。