两个宽带噪声矢量场模型的空间相关特性

任 超，黄益旺

(1.哈尔滨工程大学，水声技术重点实验室，黑龙江哈尔滨 150001；

2.海洋信息获取与安全工信部重点实验室（哈尔滨工程大学），工业和信息化部，黑龙江哈尔滨 150001；3.哈尔滨工程大学，水声工程学院，黑龙江哈尔滨 150001)

0 引 言

海洋环境噪声通常被视为声呐系统的背景干扰，在设计和应用任何声呐系统时都必须考虑其影响。阵增益是声呐阵列重要的性能参数之一，与环境噪声空间特性密切关联。由于宽带信号所携带的目标信息更多，抗干扰能力更强，更加方便于目标检测识别和参数估计，因此宽带信号在声呐领域受到了广泛的应用。由于各种类型的声呐系统拥有不同的工作频段，对其造成干扰的环境噪声频段也各不相同，而目前大多数的海洋环境噪声模型都是针对窄带噪声而建立的[1-4]，因此研究任意频段噪声场的空间相关性具有实际意义。早期Cron等[5]基于C/S模型利用频域积分来获得带宽内能量分布均匀的宽带噪声空间相关系数，在高频段、高海况、附近无船的情况下，此时风成噪声为主要影响因素，更贴近模型的假设，理论结果与实测结果符合更好。近年来，傅里叶合成技术常被用于计算海洋环境噪声场的时间互相关函数[6-8]，并利用噪声场互相关函数提取声场的多途结构以获取海底分层结构信息。Buckingham[6]认为实际观测到的海洋环境噪声通常是受带宽限制的，利用傅里叶合成技术分析了限带各向同性噪声以及深海表面噪声的互相关函数。Nichols等[9]通过时域建模推导出各向同性噪声场中的时间相关函数，这可直接获得噪声相关性。文献[10-11]从时域入手，建立了水平分层介质中宽频带表面噪声模型，分析了带宽和频谱特性对宽频带噪声空间相关性的影响，实验与仿真结果吻合较好。

对于传统水听器阵列，噪声声压场的相关特性是主要的关注对象。事实上，随着声矢量传感器的发展，仅仅对噪声声压场空间特性进行研究已无法满足当前需求。迄今为止，国内外学者已经对单频均匀各向同性噪声矢量场空间相关特性进行了大量研究[12-15]，对水平分层介质中噪声矢量场的空间相关特性问题也取得了一定成果[16-17]。

为了揭示海洋环境噪声矢量场在不同频段的空间相关性，区别于窄带噪声场的建模方法，本文通过时域声场建模，考虑简谐平面行波场声压与质点振速的关系，得到噪声场的时域声压和质点振速，从而获得任意频带噪声矢量场的空间特性。根据理想限带白噪声的时间自相关函数，本文推导出频带可调的各向同性噪声和表面噪声矢量场竖直方向空间相关系数的解析表达式。

1 噪声矢量场相关特性建模

1.1 模型理论

在均匀无限介质中，假设曲面S(r)上均匀分布着若干个统计特性相同但空间互不相关的面元噪声源，其中r代表曲面上任意一点的空间矢径，表示面元噪声源在曲面上的位置。面积为dS的面元噪声源在与其距离为R的接收点处的声压可表示

式中：ps(t，r)表示r点处的单位面积面元噪声源在单位距离处的声压；G(θ)表示噪声源的指向性函数，θ表示极角，对于各向同性噪声，噪声源无指向性，G(θ)=1；对于表面噪声，噪声源存在指向性，通常令G(θ)=cosmθ。r1、r2表示空间任意两接收点位置，以r1、r2连线的中点作为原点，可得在球坐标系下两接收点处来自曲面S(r)上所有噪声源作用下的声压及质点振速为

式中：u1、u2为方向向量。若y1、y2均可看作是平稳随机过程，则有噪声矢量场时空相关函数：

其中：·为时间平均，τ12表示声波在两个接收点间的传播时延。由于曲面上面元噪声源空间不相关，因此：

δ为狄拉克(Delta)函数，将式(5)代入式(4)中可得：

其中，U=[1u]T[1uT]。

式(6)中，Rs为面元噪声源辐射噪声声压时间自相关函数。由此可知，当已知目标频段内Rs时，可通过对面元噪声源进行面积分获得给定频带噪声矢量场的空间相关系数。接下来，将以此为基础分别讨论宽带各向同性噪声矢量场和表面噪声矢量场的空间相关特性。

1.2 各向同性噪声模型

各向同性噪声模型如图1所示。假设面元噪声源均匀分布于无限大球面上，噪声源指向性函数G(θ)=1，介质均匀。将式(6)的面积分变换到球坐标系下，对方向角积分，对相关函数进行归一化处理，归一化系数取声压的方差。考虑零延时的空间相关特性，为书写简便，将归一化噪声矢量场空间相关函数记为ρ(d)，计算公式为

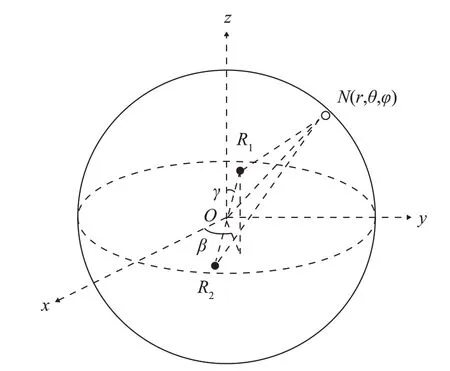
图1 各向同性噪声模型Fig.1 Schematic diagram of isotropic noise model

其中：γ、β表示空间两个接收点连线的极角和方位角，φ为接收点相对于面元噪声源的方位角，ρs(τ)为噪声源辐射声压的归一化时间相关函数。

假设噪声源辐射限带白噪声，并且在频带[ω1，ω2]和[-ω2，-ω1]范围内，其功率谱密度为单位值，则可得到该限带白噪声归一化时间相关函数为

将式(9)代入式(7)中，有：

考虑噪声矢量场竖直方向的相关特性，即令γ=0，此时τ12=dcosθc，则式(10)可简化为

其中：k1=ω1c，k2=ω2c。则可推导出声压与声压、声压与质点振速、质点振速分量间的相关函数分别为

其中：函数Si(x)的表达式为

式(12)～(14)中，ρij中i、j取值分别为1、2、3、4，分别代表声压以及x、y、z方向的质点振速。当k2→k1时，使用洛必达法则，对式(12)～(14)等号右侧取极限，得到的结果即为窄带各向同性噪声矢量场归一化空间相关函数，其结果与文献[14]的结果一致，式(12)也与文献[5]中给出的使用频域积分获得的宽带各向同性噪声空间相关系数表达式一致，可充分证明结果的正确性。式(12)～(14)中的相关函数均为实函数，除上述分量外相关函数矩阵中其余分量的实部恒等于0，表明各向同性噪声矢量场在竖直方向上只有声压与声压之间、相同质点振速分量之间是相关的。

1.3 表面噪声模型

表面噪声模型示意图如图2所示。假设面元噪声源均匀分布于无限大海面上，海水介质均匀。

图2 表面噪声模型示意图Fig.2 Schematic diagram of surface noise model

将式(6)的面积分变换到极坐标系下的方向角积分，考虑零时延的空间相关特性，对相关函数做归一化处理后得到：

式中：归一化常数C的表达式为

噪声源辐射声压的归一化时间相关函数如式(9)所示，则有：

对于噪声矢量场竖直方向的相关特性，当G(θ)=cosθ时，C=π时，式(18)改写为

积分后得到声压与声压、声压与竖直方向质点振速分量、同一方向质点振速分量之间的相关函数，表达分别为

当k2→k1时，对式(20)～(23)取极限得到与文献[15]一致的结果。同样式(20)也与文献[5]中给出的宽带表面噪声空间相关系数表达式一致。

当噪声源指向性G(θ)=cos2θ时，C=π2时，式(18)改写为

积分得到声压与声压、声压与竖直方向质点振速分量、同一方向质点振速分量之间的相关函数为

由上述结果可知，表面噪声矢量场在竖直方向上只有声压与声压、声压与z方向的质点振速、相同质点振速分量之间是相关的。

2 噪声矢量场的空间相关系数

针对各向同性噪声和表面噪声模型，考虑1 000 Hz窄带噪声以及频带为500～1 500 Hz的限带白噪声的空间相关特性。在表面噪声模型中，假设噪声源指向性分别为cosθ和cos2θ。噪声场竖直方向上的空间相关系数可采用上文中的解析表达式计算获得，对于水平方向及其他任意方向，则采用数值积分方法计算相关系数。在水平方向的相关系数的计算中，取β=π6。窄带和宽带各向同性噪声及表面噪声矢量场空间相关系数计算结果分别如图3～5所示。

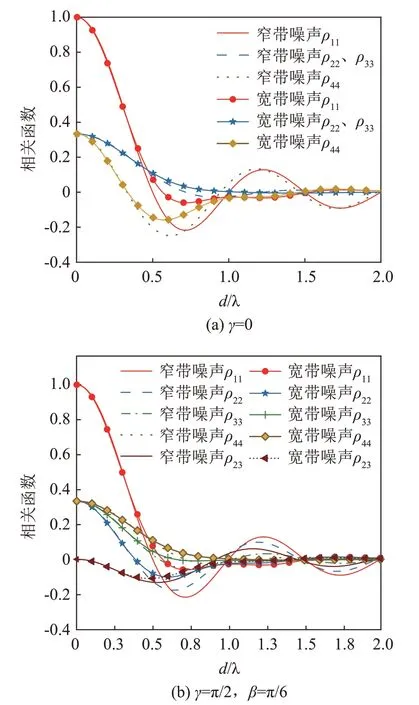
图3 各向同性窄带和宽带噪声矢量场空间相关特性Fig.3 patial correlations of narrow-band and broadband isotropic noise vector fields

2.1 宽带各向同性噪声

从图3中可以看出，对于各向同性噪声场，其声压空间相关系数与空间方向无关，而质点振速分量的自相关和互相关系数与基阵的俯仰角、水平方位角是相关的。当γ=π2时，竖直方向的质点振速分量与水平两个方向的质点振速分量均不相关，而水平两个方向的质点振速是相关的。

对比宽带和窄带各向同性噪声矢量场的空间特性可知，在竖直及水平方向上，两类噪声矢量场的空间相关半径基本相同。相较于窄带噪声，宽带噪声的矢量场空间相关系数的振荡幅度更小；当水听器间距较大时，宽带噪声矢量场空间相关系数起伏更快地趋于平稳。由于宽带噪声矢量场的空间相关函数也可认为是频带内所有频率的窄带噪声矢量场空间相关函数的频率积分[5,11]，其归一化后的相关系数代表了一定带宽内噪声的总体相关性。不同频率的窄带噪声波长不同，其矢量场空间相关函数极大值与极小值的位置也不相同，在进行频率积分时，不同频率的窄带噪声矢量场空间相关函数相互叠加、相互抵消才导致上述现象的发生。

2.2 宽带表面噪声

从图4、5中可以看出，对于表面噪声场，在水平方向上，声压与声压、声压与z方向的质点振速以及相同质点振速分量之间是相关的，且水平两个方向的质点振速也是相关的；声压与声压、声压与z方向的质点振速的相关性仅与俯仰角有关，而质点振速分量以及水平两个方向的质点振速的相关特性与基阵的俯仰角和方位角均有关。

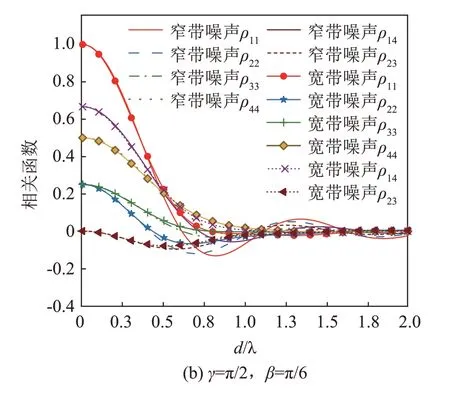
图4 窄带和宽带表面噪声矢量场空间相关特性(G(θ)=cosθ)Fig.4 Spatial correlations of narrow-band and broadband surface noise vector fields when G(θ)=cosθ

图5 窄带和宽带表面噪声矢量场空间相关特性(G(θ)=cos2θ)Fig.5 Spatial correlations of narrow-band and broadband surface noise vector fields when G(θ)=cos2θ

宽带和窄带表面噪声矢量场的空间特性差异与各向同性噪声矢量场基本一致。比较图4(a)、5(a)可以看出，噪声源指向性G(θ)=cos2θ的表面噪声矢量场竖直方向上的空间相关系数的振荡幅度明显大于噪声源指向性G(θ)=cosθ的表面噪声矢量场，空间不同位置声场的相关性差别更大，特别是对于窄带噪声，可知噪声源指向性会对表面噪声矢量场竖直方向空间相关系数产生较为显著的影响。

3 结 论

为了计算宽带海洋环境噪声矢量场空间相关系数，本文针对各向同性噪声和表面噪声模型开展了理论和仿真研究。采用时域建模方法，获得了单个面元噪声源的辐射声场。在统计特性相同的相互独立的噪声源在曲面上均匀分布的假设条件下，得到了宽带各向同性噪声及表面噪声矢量场空间相关系数的积分表示。对于表面噪声，噪声源通常具有cosmθ的垂直指向性，文中分别讨论了m=1和m=2两种情况。对于限带白噪声这种简单情况，文中给出了噪声矢量场竖直方向空间相关函数的解析表达式。对于方位角30°的水平方向，则采用数值积分方法计算噪声矢量场各分量的空间相关系数。两个特殊方向上的计算结果表明，对于各向同性噪声和表面噪声，宽带噪声矢量场各分量的空间相关系数的振荡幅度小于窄带噪声；噪声源指向性对表面噪声矢量场各分量竖直方向上的空间相关特性的影响显著。

本文对比研究了宽带及窄带各向同性噪声及表面噪声矢量场空间相关特性的差异。除此之外，影响实际海洋环境噪声场特性的因素还有海水、海底的声学参数等。本文的研究仅是海洋环境噪声的简单模型。