基于蝠鲼算法的散货货棚空间桁架轻量化设计

熊宏武 孙 文 蔡大鹏 张立朝 肖佩弦

(中国铁建港航局集团有限公司1) 珠海 519000) (武汉理工大学土木工程与建筑学院2) 武汉 430070)

0 引 言

空间桁架结构通过杆件之间传递轴力来抵抗外荷载,是一种能够采用较少材料而获得较大内部空间的结构形式,对桁架结构进行优化设计还可以进一步节省材料、改进设计质量.桁架结构的优化包括构件尺寸优化、结构形状优化及结构拓扑优化.文中将利用智能优化方法对一个792根杆件组成的空间桁架结构进行构件尺寸优化设计.

结构优化设计既通过不断调整方案找到最好的设计,但最优设计需要满足一定的条件,该条件被称为约束,寻找满足最优设计的过程就是结构优化.相较于传统的基于梯度算法寻优的方法,结构智能优化基于群智能搜索算法,具有鲁棒性好、扩展性和广泛的适用性等特点.在不存在集中控制并缺少局部信息和模型的情况下,为解决复杂分布式问题提供了思路,不要求目标问题是连续的凸函数[1].随着结构智能优化学科的发展,大量元启发算法的提出或改进,诸如模拟退火算法[2]、粒子群算法[3]、樽海鞘种群算法[4]、人工鱼群算法[5]、蚁群优化算法[6]等在结构优化设计领域都有大量的应用案例.

蝠鲼觅食算法Zhao等[7]提出的新型仿生群智能搜索算法,该算法模拟了大型海洋生物蝠鲼的觅食过程,蝠鲼通过链式觅食、旋风式觅食和翻筋斗式觅食三种策略捕获海洋中的浮游生物.得益于三种搜索策略,蝠鲼觅食算法可以准确的在复杂解空间中搜索到群体最优解.

文中将蝠鲼觅食算法与IDeath penalty和IDeb rule技术结合应用于钢制散货货棚的空间桁架结构优化中,并对优化前后的结构用钢量进行评估.

1 散货货棚工程概况

1.1 散货货棚空间结构原始设计

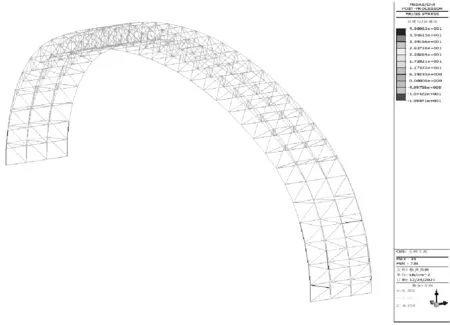
图1为一个792杆的空间桁架的初步结构设计和边界条件.散货货棚由12片类似的钢网架组成,对一个标准单元进行优化,其余钢网架采用相同优化设计.

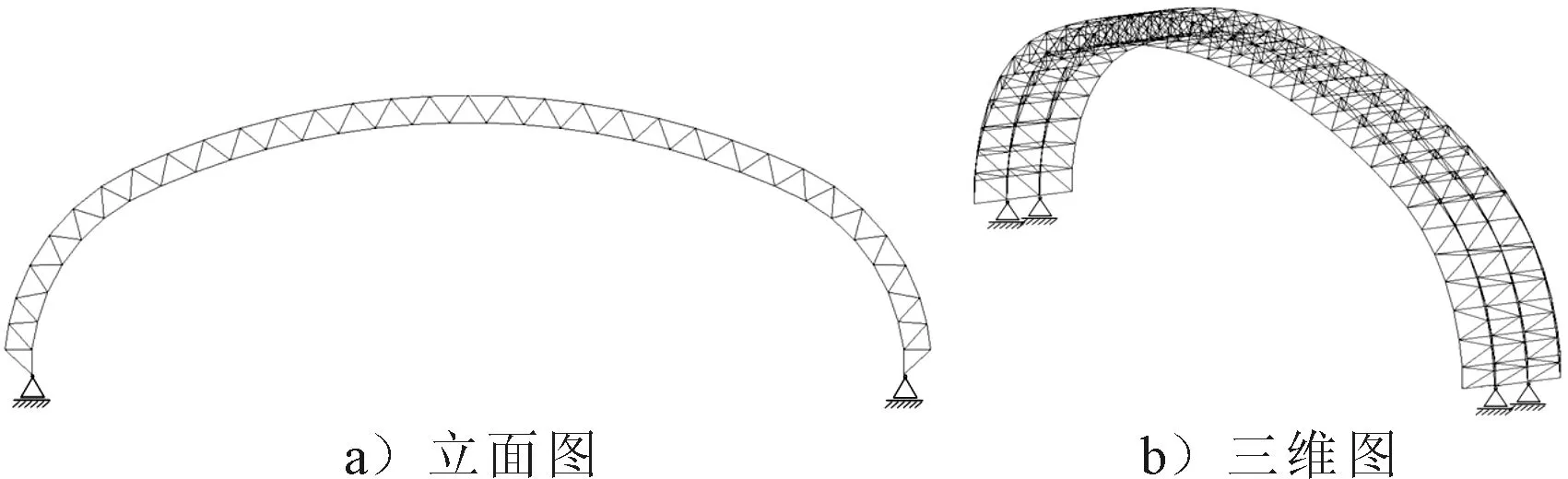
图1 散货货棚立面图和三维图

792根杆件被分为10组类,初始设计截面尺寸见表1,结构的材料采用Q235钢材,原始设计整体用钢量为39 039.9 kg.

表1 初始设计截面尺寸表

施加在桁架上的荷载工况有五种,荷载取值见表2.

表2 荷载工况表

1.2 原始设计结构分析

通过midas Civil建模进行结构分析,原始设计在五种工况组合作用下,桁架单元应力图见图2.

图2 原始设计桁架单元应力图

由图2可知:各个杆件应力均未超过Q235钢材容许应力±160 MPa.在五种工况单独作用下,最大变形发生在风载单独作用时,最大变形为65 mm.

原始设计是根据设计经验拟定的初步设计,并非最优设计,为了得到更为节省材料且受力更合理的结构,采用优化算法对原始设计进行尺寸优化.

2 MRFO算法

2.1 仿生原理

MRFO算法通过对蝠鲼觅食过程中所形成的奇妙而智能的觅食策略进行抽象成数学模型,从而实现仿生搜索过程.算法共有三种策略:

第一种觅食策略是链式觅食,见图3.当多条蝠鲼开始觅食时,它们首尾相连排成一条整齐的队伍.当排在前面蝠鲼遗漏的食物会被后面的蝠鲼抓起.通过相互合作,它们可以将最多的浮游生物吸入鳃中,提高食物捕获率.

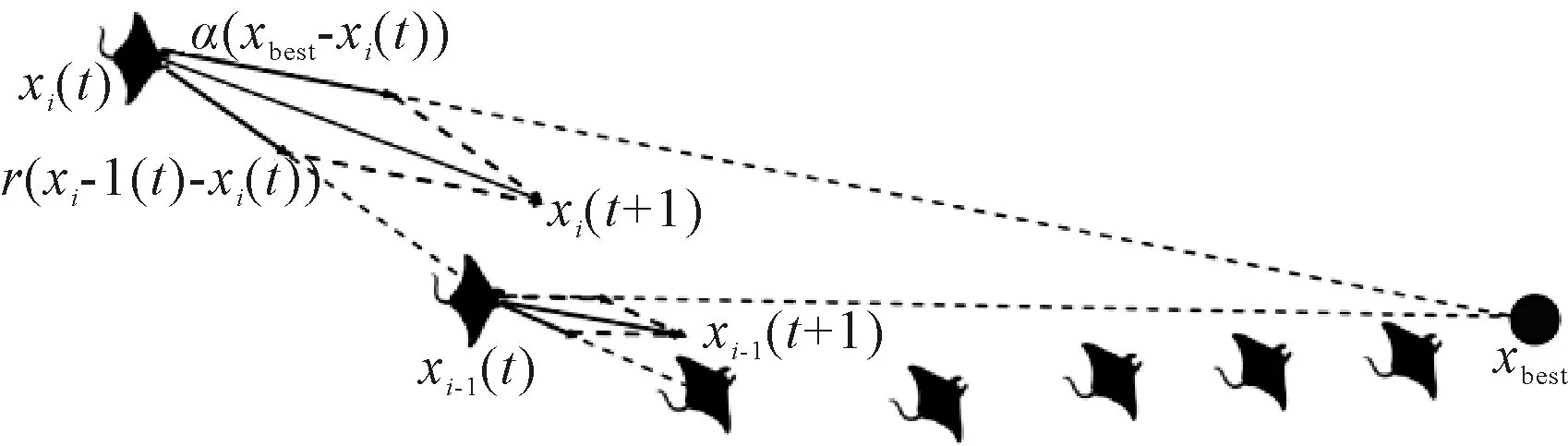
图3 链式觅食示意图

第二种觅食策略是旋风式觅食,见图4.当浮游生物的浓度很高时,几十条蝠鲼聚集在一起.它们的尾部与头部呈螺旋状连接,在旋涡中心形成一个螺旋顶点,过滤后的水向表面移动.这会把浮游生物拉进它们的口中.

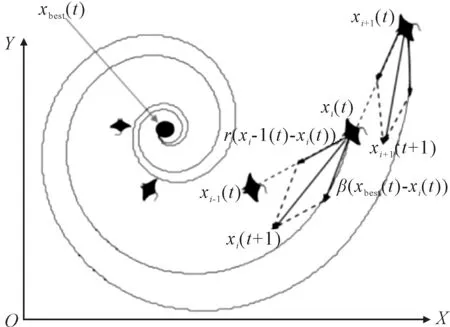
图4 旋风式觅食示意图

图5为最后一种觅食策略是翻筋斗式觅食.当蝠鲼找到食物来源时,它们会做一系列的逆流运动,围绕食物旋转,将其吸引到身边.空翻是一种随机、频繁、局部和周期性的运动,有助于蝠鲼摄入食物.

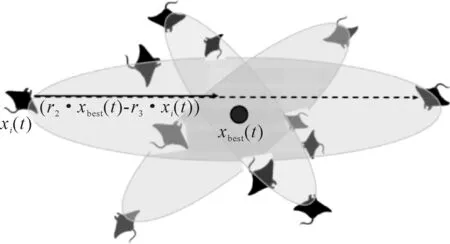
图5 翻筋斗式觅食示意图

前面两种觅食策略可以使蝠鲼不断靠近食物,最后一种策略有助于捕获食物[8],蝠鲼通过交替使用以上三种觅食策略,可以最大程度的捕获最多的食物.

2.2 算法更新公式

第一阶段,随机采用前两种策略进行更新,若认为群体最优既为食物的位置,该阶段则以食物和前一条蝠鲼为目标更新位置.先生成一个随机数r1,当r1>0.5时,采用链式策略公式进行更新.

(1)

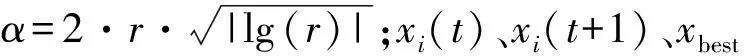
否则采取旋风式更新当前位置,旋风式搜索又分为

(2)

xrand=x1+rand·(xu-xl)

(3)

(4)

第二阶段则采用翻筋斗策略公式更新位置,该更新过程只与上一次以及食物的位置有关,蝠鲼将围绕食物的位置作翻转运动.

xi(t+1)=xi(t)+S·(r2·xbest-r3·xi(t))

(5)

式中:每一只蝠鲼的位置代表一种设计方案,食物的位置代表当前目标值最优的设计.S为翻转系数,一般取定常数2;(r2·xbest-r3·xi(t))为第i个设计与当前最优设计的距离,式(5)的物理含义为以2倍该设计与当前最优设计的距离为半径进行翻转,并以随机数r2、r3进行扰动.

3 约束处理技术

3.1 两种约束处理技术

无约束化处理的思路就是将有约束优化问题转化为等价的无约束优化问题[9-10].罚函数法是最常用的约束处理技术,实现方便,对问题本身没有苛刻要求,其思想是给违反约束的解施加一个惩罚系数加入目标函数中.

Φ(x)=f(x)+λ·φ(x)

(6)

式中:f(x)为优化目标函数;φ(x)为约束函数;λ为惩罚因子

常用的设置方法有定常罚函数法、动态罚函数法、适应性罚函数法等.本文选用的Death penalty方法是罚函数法的一个变种,要求初始解均为可行解,并在迭代过程中认为惩罚因子取为无穷大从而淘汰所有的非可行解.

此外,可行性规则Deb rule是一种常用的无参数约束处理技术,它给出了三条挑选可行解的规则:①可行解优于不可行解;②目标函数值小的可行解优于目标函数值大的可行解;③两个不可行解之间,违反约束程度更小的解为优.可行性规则给出的三条规则中,①③引导搜索向可行域进行,②引导搜索向更满足目标的方向进行.

3.2 改进的两种约束处理技术

基于结构优化的特点,对于一个设计,优先计算其目标函数值,当目标函数值优于当前最优时,才计算其约束函数值再做进一步判断,可以达到提高搜索效率,避免在冗余步骤上浪费计算资源的效果.

改进后的可行性规则,其伪代码如下.

初始化优化参数及种群,更新xi(t+1),计算xi(t+1)的目标函数值f(xi(t+1)),

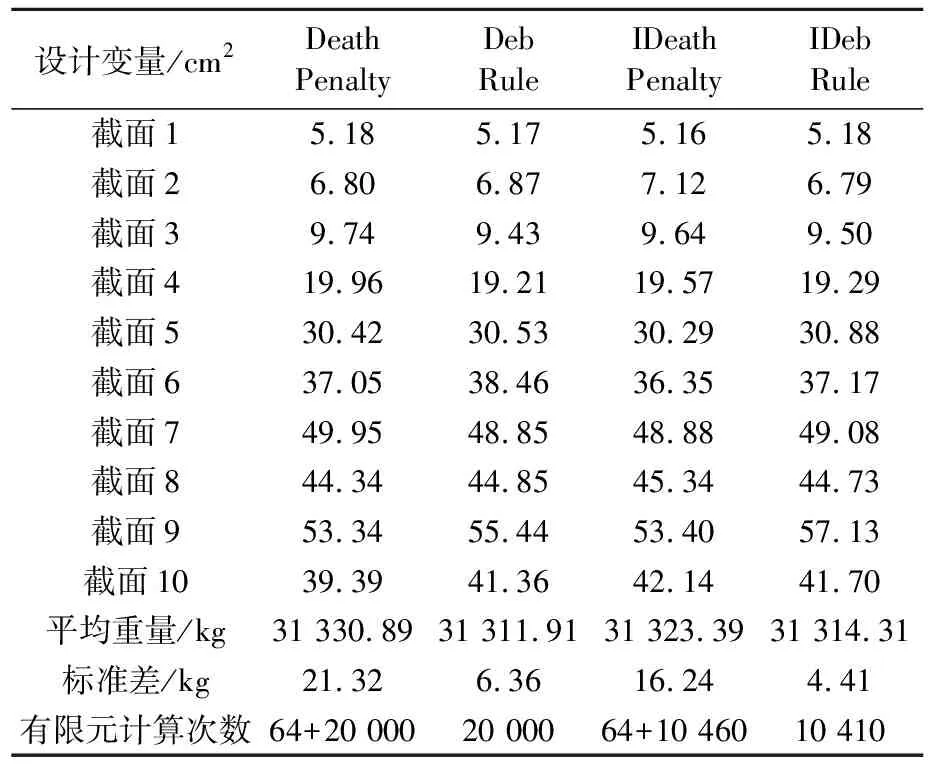
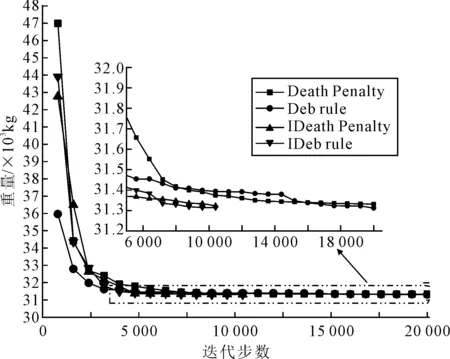
如果f(xi(t+1))

则计算xi(t+1)的约束函数值φ(xi(t+1)),如果φ(xi(t+1))满足约束条件,则保留xi(t+1),否则舍弃该解,保留原解xi(t).

重复上述过程,直至满足迭代条件.

4 散货货棚优化设计

4.1 散货货棚空间结构优化模型

钢材Q235的材料密度和弹性模量分别为7 800 kg/m3和206 GPa.施加在桁架上的荷载工况有五种,取值与布置方式与原始设计保持一致.

约束条件包括桁架的刚度和强度要求,所有杆件的拉压应力不应超过Q235钢材的容许应力±160 MPa.根据原设计结构分析的结果,限制所有自由节点在各个方向上的容许位移不大于65 mm.设计变量为十组桁架构件的横截面积,取值范围由1.0～100.0 cm2.为了得到重量最轻的设计,采用MRFO算法对其进行尺寸结构优化设计.

4.2 优化结果讨论

基于MRFO算法分别采用四种约束处理技术,对该散货货棚桁架结构进行50次优化,每次优化最大迭代步数为20 000步,初始种群大小取25,得到50次优化结果的均值见表3,图6为收敛曲线.

表3 792杆桁架优化结果

图6 792杆桁架优化收敛曲线图

对优化后的设计用midas Civil进行结构分析,桁架应力图见图7.最大与最小应力为出现在屋面活载工况时为159.40和-55.92 MPa,均低于材料容许应力,最大变形为屋面活载作用下节点向下的65.00 mm,可知该结构最终截面尺寸是由强度和刚度要求共同控制.

图7 优化后设计桁架单元应力图

5 结 论

1) 优化数据结果显示,采用蝠鲼觅食优化算法(MRFO)优化后散货货棚结构的重量较原有设计减轻了约19.7%,结构的材料分配更复合力学原理.

2) 通过50次在桁架优化问题上的测试结果表明,蝠鲼觅食优化算法是非常有效和可靠的,具有稳定的收敛性能和搜索精度.

3) 改进后的两种约束处理技术(IDeath penalty与IDeb rule),将算法的搜索效率提高了近50%,剔除了一半不必要的有限元计算,节省了计算资源.

4) 虽然改进后的约束处理技术加快了算法的收敛速度,但未对搜索结果的精度起到太多的作用,后续值得进一步研究.