基于底板束预张拉的大跨PC连续刚构桥新型合龙技术

胡志坚 刘宇航 夏雷雷

(武汉理工大学交通与物流工程学院 武汉 430063)

高墩大跨预应力混凝土连续刚构桥合龙后,桥体将由静定结构转变为超静定结构,内力与合龙前极大不同.在合龙过程中,配重是一个关键步骤.配重的主要作用是:确保合龙段混凝土浇筑过程中,合龙口不发生位移,保证合龙段线形平顺.合龙口发生位移,底板混凝土易出现横向裂缝,会产生安全隐患,影响施工质量.

现有研究在使用配重物时通常使用水箱或沙袋,少数情况下也使用挂篮.使用沙袋或挂篮配重时,因合龙段混凝土浇筑过程中卸载不方便或挂篮移动速度不易控制等原因,实际工程中多采用水箱配重.针对配重大小的计算,张新志等[1]描述了等重量配重法的原理,即施加与合龙段混凝土相等重量的方法,其配重大小容易确定.张谢东等[2]在合龙计算时采用等重量法配重.邬彪红[3]采用等弯矩配重法计算压重,并顺利合龙.朱世峰[4]提出等位移法配重,使合龙段两端悬臂在浇注合拢段砼时不发生相对位移.李定伦[5]以水箱重量作为变量,给出等位移配重法配重与合龙段重量的理论关系式,以及三跨连续刚构桥配重的理论计算公式.赵成升等[6]选择在水箱压重后,临时张拉纵向预应力束,以抵消温度降低时梁体两端对合龙段新浇筑混凝土的影响.但是对于地势恶劣的施工环境或取水困难时,最好能提出一种不需要配重的合龙方式,使得合龙后成桥线形和内力满足桥梁设计要求.

文中提出一种基于箱梁底板束预张拉的新型合龙技术,从而取消合龙配重.即提前分批张拉底板预应力束,达到与水箱配重消除合龙口位移同样的效果.并以合龙口不发生扰动作为控制条件,通过合龙前、浇筑混凝土后以及成桥后全桥线形和应力状态的实桥对比分析,确保使用新型合龙技术的可行性和可靠性.

1 原 理

新型合龙技术因取消配重,中跨合龙施工顺序为:安装吊架→锁定劲性骨架→混凝土浇筑(同时预张拉部分底板钢束)→混凝土养护→拆除劲性骨架→后续底板束张拉.变截面连续刚构桥合龙段的劲性骨架焊接后,两悬臂间具有连接,合龙段截面刚度即为劲性骨架的整体刚度.合龙段混凝土浇筑后可将其简化为集中荷载G作用于合龙口位置.底板预应力筋张拉后锚固于梁体上,预应力筋张拉效应可分解为两部分:①预应力筋沿程的等效竖向荷载q;②作用于合龙束锚固点压力T.见图1.

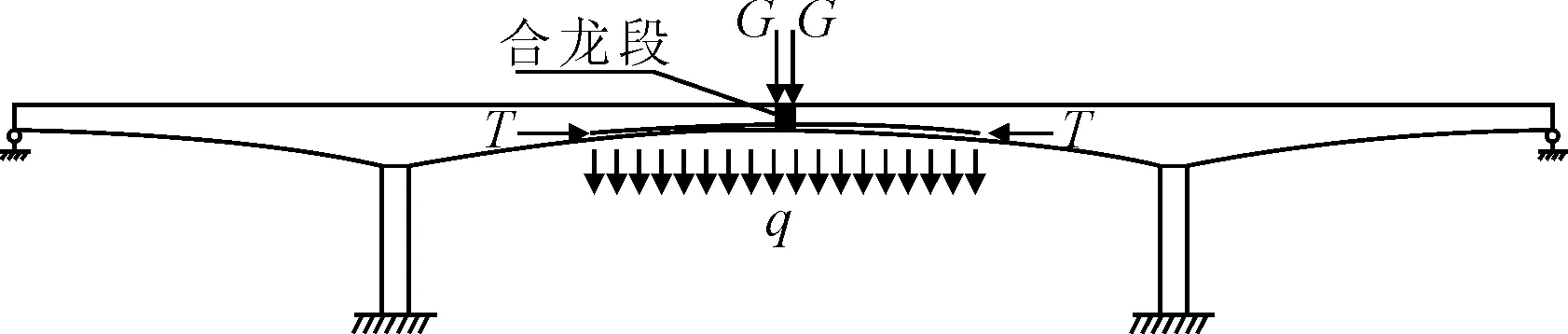
图1 梁体受力图

计算等效竖向荷载q时,可以认为预应力束为图2的弧线[7],取微端dL分析.

图2 等效竖向荷载分析示意图

得到

q=T/R

式中:T为预应力束张力;R为底板曲线半径.

底板合龙钢束按照底板曲线布置,此时预应力钢束张拉后会产生上拱效应,位移效应见图3.

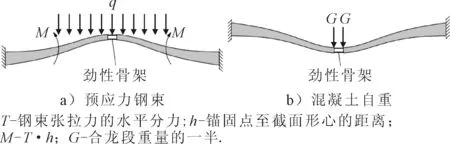
图3 位移效应示意图

合龙口位移可使用力法进行位移求解,剪力和轴力引起的竖向挠度忽略不计.每根钢束单独作用于梁体时合龙口竖向位移值Δfi,湿重作用下合龙口产生的挠度为ΔfG.根据叠加法原理,合龙段混凝土浇筑时合龙口位移值Δf=∑Δfi+ΔfG.

合龙段混凝土浇注过程中同步张拉的底板钢束选取需遵循以下原则:①选取长束,减小张拉过程中钢束对合龙口附近块段的劈裂效应;②选取对合龙口竖向位移影响较大的钢束,以此减小合龙过程中所需张拉力.

2 工程应用

2.1 工程概况

某特大桥桥孔布置为90 m+2×160 m+90 m,见图4.主桥上部结构采用变截面单箱单室箱梁,箱梁断面采用直腹板断面.墩顶处梁高9.4 m,合龙段及及边墩现浇段高3.8 m,梁段高按1.8次抛物线(y=3.8+5.6x1.8/761.8)变化;跨中底板厚度为32 cm,根部底板厚度为130 cm,其间按1.8次抛物线(h=0.32+0.000 403 424x1.8)变化.主梁采用C55号混凝土;跨中底板共布置15束纵向预应力束,均用直径15.2 mm高强度、低松弛钢绞线,抗拉强度标准值fpk=1 860 MPa;边跨底板纵向束为6股,中跨底板纵向束为15股;纵向钢束张拉控制应力采用1 395 MPa;钢束曲线与底板曲线平行,在横截面上对称布置.

图4 全桥立面图

中跨底板预应力束由15束(编号Z1～Z12、Z3’～Z5’,其中Z3～Z5与对应附加束Z3’～Z5’,各自平弯竖弯曲线一致,认为其单独效应相同)组成,边跨底板预应力束由6束(编号B1～B6)组成,图5为钢束布置图和梁体阶段编号.

图5 中跨钢束束布置图

2.2 单根钢束作用位移效应值

因湿重混凝土作用下边跨合龙中边跨合龙口位移仅为ΔGB=0.20 mm,位移影响很小,故本文仅分析中跨合龙段.中跨合龙口混凝土浇筑后产生的位移为ΔGZ=6.46 mm.选取14～20节段内所有底板束作为合龙用钢束.表1为不同张拉应力下各钢束张拉对应的合龙口位移效应值.张拉应力上限值取文献[8]规定的钢束最大初应力,即张拉控制应力的25%.

表1 合龙口位移效应值

2.3 合龙施工阶段分析

提取混凝土浇筑完成后中跨各截面位移计算值,结果见图6.

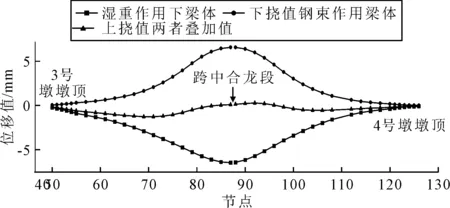
图6 新型合龙技术中跨各截面位移值

由图6可知:湿重混凝土作用下,中跨各截面均产生一定下挠,在合龙口附近下挠值最大.使用本文方法合龙,在合龙口附近基本未发生扰动.选取跨中附近四个截面作为分析对象,其位移值见表2.

表2 跨中附近截面位移变化值 单位:mm

由表2可知:若直接合龙,中跨截面均产生一定下挠值,最大为6.45 mm位于合龙口处;使用本文方法合龙,合龙口位移仅为0.09 mm,可有效消除合龙段浇筑时合龙口的扰动,减少浇筑过程对未成形混凝土的影响.

2.4 成桥累计变形

新型合龙技术施工过程中,待合龙段混凝土达到设计规定强度后,对预张拉钢束进行放张处理[9].提取配重作用以及钢束放张中跨各截面下挠计算值,见图7.由图7可知:配重产生的中跨累计下挠值远大于放张产生的下挠值,两者差值在墩顶处最小,越靠近合龙口越大,最大差值为17 mm.

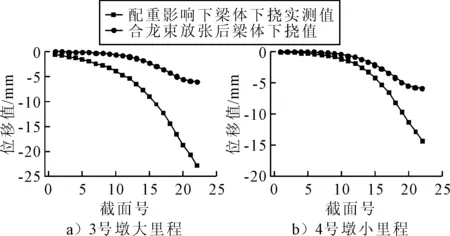
图7 不同作用下梁体位移值

本文方法没有配重这一步骤,故与传统配置合龙施工方法的累计变形值有明显区别.本文计算得到成桥后累计位移最大差值为17.1 mm,位于图8的3号墩大里程合龙口处.

图8 成桥累计变形值

图8中合龙口两个悬臂端变形值不对称,这是因为边跨合龙已经完成,3号墩与4号墩所对应的受力体系不同所致.

2.5 全桥应力分析

该桥为单向三车道布置,根据文献[10]计入横向车道布载系数及纵向折减系数施加车道荷载.计算活载效应时,取最不利荷载工况分析,车道荷载作用下,全桥底板最大拉应力为2.48 MPa,位于跨中底板处,见图9.由图9可知:使用本文方法合龙,桥体经过10年收缩徐变的作用,跨中压应力储备为5.32 MPa,使用新型合龙技术成桥后的桥体完全满足设计要求.相较于等位移配重法,在中跨跨中底板压应力差值最大为0.37 MPa,见图10.如需加大压应力储备,可进一步通过底板预应力束设计实现.但根据文献[11],连续刚构桥跨中底板压应力储备不是越大越好,其合理范围在2～3 MPa,从压应力储备角度来看,本文合龙方法优于传统方法.

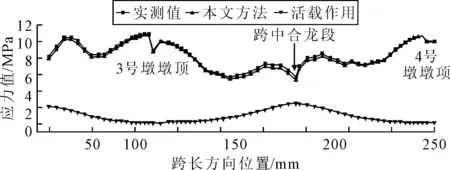
图9 10年收缩徐变及活载作用全桥下缘应力计算值

图10 成桥十年过程中跨中合龙段底板压应力变化图

3 结 论

1) 基于箱梁底板束预张拉的新型合龙技术可完全取消配重,方便施工,完全满足设计要求.

2) 新型合龙技术在合龙过程中保持合龙口不发生扰动,减少浇筑过程对未成形混凝土的影响,保证合龙段质量.

3) 与传统技术相比,使用新型技术合龙全桥底板压应力没有明显减少,且更优于传统方法.