基于哈里斯鹰优化算法的多GNSS快速选星方法

杨 光，屈德新*，张更新

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003；2.南京邮电大学 通信与网络技术国家地方联合工程研究中心，江苏 南京 210003)

0 引言

随着全球导航卫星系统(Global Navigation Sate-llite System,GNSS)的快速发展,越来越多的领域将GNSS运用到工程当中,从而使得更多的人从中受益。然而,在导航系统快速发展的同时,为了提高适用性以及可靠性,对该系统的要求也越来越严格,其中就包括更短的定位耗时以及更高的定位精度。由此,全世界各个有能力的国家都将发展自己的导航卫星列为国家的长期发展规划。截至目前,全球已经建成了4套完善的全球定位系统:中国的BDS、欧盟的Galileo、俄罗斯的GLONASS以及美国的GPS,已有超过120颗全球导航卫星在轨运行,能够实现在同一地点有多颗卫星为用户提供服务。然而,随着可见星数量的快速增加,如果将所有可见星同时应用到定位中去,计算效率将会大幅度降低,其对定位精度的提升效果有限,因此,如何快速地从所有可见星中选出最优构型成为一个热门问题。

选星是在获取当前所有可见星位置、钟差等信息后,确定一定数量的卫星参与定位解算的过程。传统选星过程以最小几何精度因子(Geometric Dilution of Precision,GDOP)遍历法[1]为基础,此外还有最大四面体体积法[2]、最大行列式法[3]、几何布局算法[4]、最优GPS递归算法[5]、GPS/Galileo组合导航定位系统选星算法[6]等。目前主要还是依据最小GDOP准则进行选星操作,然而如何简化选取拥有最小GDOP值的卫星组合成为了一个急需解决的问题。Mosavi等[7]提出了基于进化算法(EA)的自适应滤波技术来计算GDOP的方法,但该方法存在一定的误差。宋丹等[8]提出了一种基于遗传算法的选星方法,该方法能够快速准确地实现多个GNSS下选星颗数大于4的选星。徐小钧等[9]提出了一种将选星数目和GDOP值同时作为目标的基于NSGA-II遗传算法的多星座选星方法,该算法能够综合优化GDOP和选星数目,同时保证较小的计算量和更高的定位精度。张兆龙等[10]提出了一种将BP神经网络和遗传算法结合的选星算法,既大大减小了计算量,又增加了选星的准确率。王尔申等[11]提出了一种基于人工鱼群算法的粒子群优化选星算法,利用人工鱼群算法良好的全局收敛特性,克服粒子群算法易于陷入局部最优的缺点,使其准确率优于标准PSO选星算法。王晖等[12]提出了一种顾及信噪比的蝙蝠选星算法,通过设置信噪比阈值,剔除信号受干扰的卫星,结合选星算法的高效率优点,减少选星耗时。余德荧等[13]提出了一种基于灰狼优化(Grey Wolf Optimizer,GWO)算法的快速选星方法,利用自适应收敛因子和信息反馈机制,避免局部极值,能够大幅度减小计算量。石涛等[14]提出了一种利用多种群并行遗传算法(Parallel Genetic Algorithm,PGA)进行快速选择当前最优可见星组合的方法,该方法可以有效地在典型高轨环境下快速准确地完成选星。邱明等[15]提出了基于帝国竞争优化算法的双目标选星算法,通过引入可见星仰角和方向角先验信息,同时约束GDOP以及选星数,提高选星灵活度。

虽然上述算法在不同程度上提高了选星效率,但为了避免局部最优,需要多次实验寻找最优的参数配置,从而实现寻得全局最优解。哈里斯鹰优化(Harris Hawks Optimization,HHO)算法是Heidari等[16]于2019年提出的一种新型群体智能算法,整个寻优过程包括探索、探索与开发转换和开发3个阶段,具有原理简单、控制参数少和全局搜索能力出色等特点。HHO算法相较于其他成熟的元启发式技术而言,提供了非常有前途的结果,有时甚至具有竞争性,同时以灵活的结构、高性能和高质量的结果越来越受到研究人员的关注,在作业车间调度[17]、神经网络[18]、恶意软件检测[19]、定位解算[20]和结构体寿命预测[21]等领域得到广泛应用。

鉴于目前没有将HHO算法应用于GNSS系统快速选星的研究,本文将HHO算法引入到多GNSS组合导航选星过程中,建立了基于HHO算法的快速选星模型。通过对多GNSS下不同时间、不同选星颗数、HHO算法种群数以及算法迭代次数进行仿真实验,以GWO、改进粒子群算法(Improved Particle Swarm Optimization,IPSO)以及遍历法结果作为对比,验证了HHO算法的快速选星能力和高准确率。

1 HHO算法

1.1 算法背景

HHO算法灵感来源于哈里斯鹰在自然界中的合作行为和追逐方式,称为“突袭”,在该策略中,几只老鹰合作从不同方向扑向猎物,试图以出乎意料的方式将其捕获。整个搜索过程可以分为3个阶段:① 探索阶段;② 探索与开发转换阶段;③ 开发阶段。

1.2 数学模型

在每次迭代过程中,为了确定下一次位置更新策略,将拥有最优适应度值的哈里斯鹰作为猎物或者预期的猎物。

1.2.1 探索阶段

此阶段哈里斯鹰会随机飞抵某些位置,并根据2种策略探索猎物。如果每种飞行策略机会p相等,随机生成p的大小,当p≤0.5时,哈里斯鹰根据其他成员和猎物的位置进行栖息;当p>0.5时,则随机栖息在鹰群活动范围内的大树上,具体模型为:

(1)

(2)

式中:X(t+1)为下一次迭代中鹰的坐标向量,Xrabbit(t)为猎物的坐标(即拥有最优适应度的个体坐标),X(t)为当前鹰的位置向量,r1、r2、r3、r4和p为(0,1)的随机数,UB、LB为位置数据的上下限,Xrand(t)为在所有已知的鹰群中随机选择的鹰的坐标,Xm(t)为坐标的平均值,N为鹰群大小,Xi(t)为当前第i只鹰的坐标。

1.2.2 探索到开发的转换

HHO算法会从探索转到开发阶段,随后根据猎物的逃逸能量在不同的开发行为之间进行转换。猎物逃跑会导致能量下降,逃逸能量可表示为:

(3)

式中:E表示猎物逃逸能量,T为最大迭代次数,t为当前迭代次数,E0为能量初始状态,是(-1,1)的随机数。当|E|≥1时,哈里斯鹰处于探索阶段,反之进入开发阶段,进而采取不同的更新策略。

1.2.3 开发阶段

当鹰处于开发阶段时,会对之前发现的预定猎物进行突袭捕捉,同时,猎物也在尝试逃脱追捕。因此,在实际情况下会根据猎物状态采用不同的捕猎风格。HHO依据猎物的逃逸风格和哈里斯鹰的追逐策略,提出了4种策略去模拟攻击阶段。此处定义r用来表示猎物在突袭前是否有机会逃脱,当r<0.5时表示有机会逃脱,反之则没有机会。

① 软围攻

在r≥0.5且|E|>0.5时,猎物有足够的能量,但没有逃脱的机会,只能通过随机跳动来尝试逃脱,在此过程中哈里斯鹰轻柔地包围猎物,使其疲惫后再进行突袭。此行为可以建模为:

X(t+1)=ΔX(t)-E|JXrabbit(t)-X(t)|,

(4)

式中:ΔX(t)为最优个体和当前个体的差值,J为猎物逃跑时移动的距离。

ΔX(t)=Xrabbit(t)-X(t),

(5)

J=2(1-r5),

(6)

式中:r5为(0,1)的随机数。

② 硬围攻

在r≥0.5且|E|≤0.5时,猎物既没有逃脱的机会,也没有足够的逃脱能量,此时哈里斯鹰采用硬包围的方式捕获猎物,该行为可以建模为:

X(t+1)=Xrabbit(t)-E|ΔX(t)|。

(7)

图1为哈里斯鹰进行硬围攻时的示例。

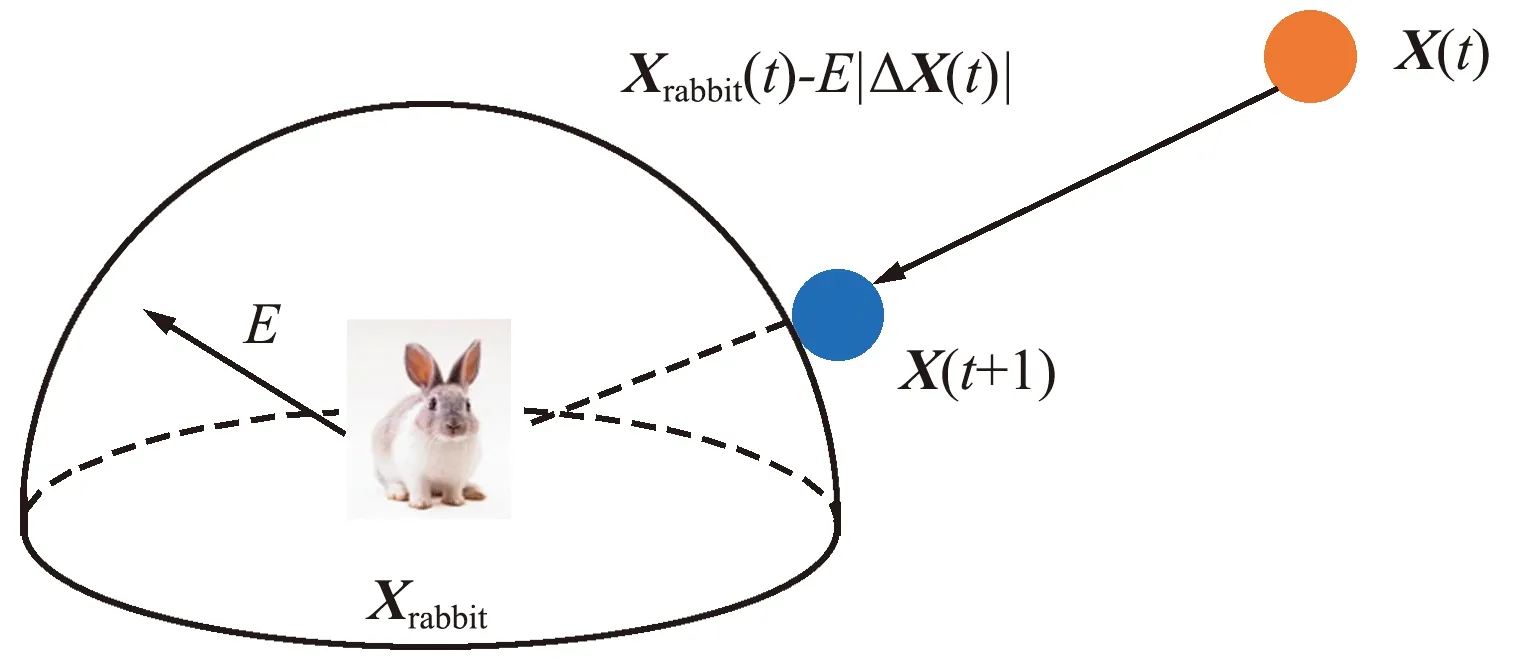
图1 硬围攻矢量示例Fig.1 Hard siege vector example

③ 渐进式快速俯冲的软包围

在r<0.5且|E|>0.5时,猎物有机会逃脱,并且有足够的能量,因此哈里斯鹰需要在进攻前形成一个更加智能的软包围圈,采用2种策略实施,根据情况选择其中一个策略。

策略1:

Y=Xrabbit(t)-E|JXrabbit(t)-X(t)|。

(8)

策略2:

Z=Y+S×LF(D),

(9)

式中:D为问题维度,S为一个D维的随机向量,LF为Levy函数。

(10)

式中:

(11)

u和v为(0,1)的D维随机向量,β=1.5,Γ( )为伽玛函数。策略选择标准如式(12)所示:

(12)

式中:F()为适应度函数,即GDOP值。

这一过程的矢量示例如图2所示。

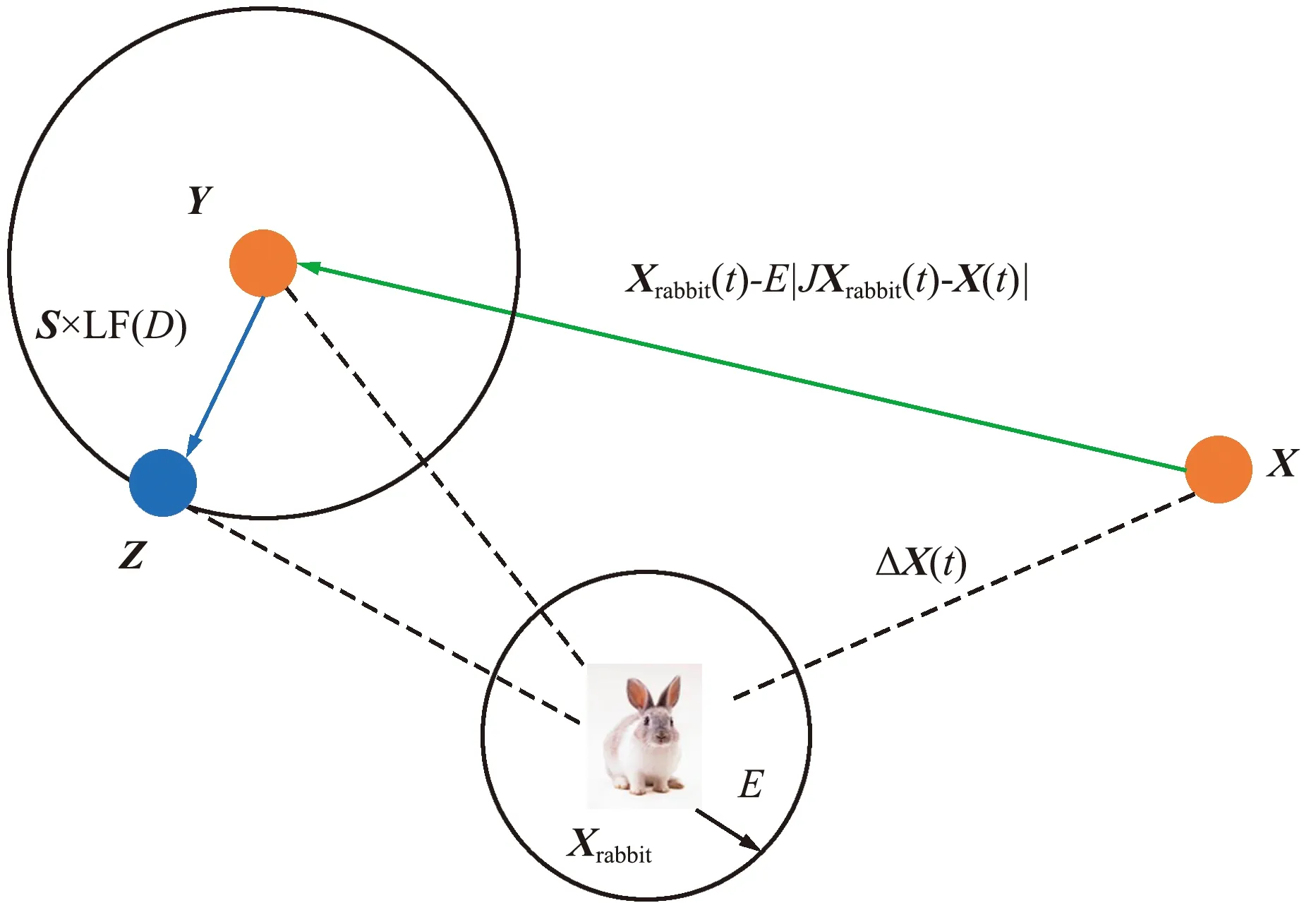
图2 渐进式快速俯冲的软包围矢量示例Fig.2 Example of soft encirclement vector for progressive rapid subduction

④ 渐进式快速俯冲的硬包围

在r<0.5且|E|≤0.5时,猎物有机会逃脱,但能量不足,此时哈里斯鹰在突袭前形成一个硬包围圈,缩小和猎物的平均距离,策略如下:

(13)

Y=Xrabbit(t)-E|JXrabbit(t)-Xm(t)|,

(14)

Z=Y+S×LF(D)。

(15)

2 基于HHO算法的快速选星方法

2.1 哈里斯鹰算法适应度函数

在多GNSS中,用户从接收机获取的自身位置精度与接收机中观测到的参与定位的卫星几何构型和伪距值有关,其中几何构型用GDOP表示。其值越小,表示利用该卫星构型进行定位时定位精度越高,因此选用GDOP值作为HHO算法的适应度函数。

(16)

式中:tr(*)表示取矩阵的迹,H为观测矩阵。在多GNSS中,同时可观测到BDS、Galileo、GLONASS以及GPS组成的多颗卫星,此时H可表示为:

(17)

式中:下标分别代表对应所属的卫星系统。假设某一个系统有n颗卫星参与定位,则此时H*为n行3列矩阵,3列分别是各个卫星与观测站连线在(x,y,z)轴上的方向余弦,1*为n行1列的纯1向量,0*为n行1列的纯0向量。

2.2 哈里斯鹰选星算法设计

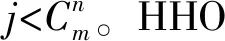
图3 HHO选星算法流程Fig.3 Flowchart of HHO satellite selection algorithm

具体的选星步骤如下:

步骤①:提取可见星。根据导航电文,获取当前仰角大于5°的所有可见星。

步骤②:编号。将获取的所有可见星按PRN由小到大编号为:1,2,3,…,m。

步骤③:初始化种群。设种群数为j,从m颗可见星中随机抽取n颗进行组合,产生j只不同的鹰构成一个种群。

步骤④:计算适应度值。计算每只鹰对应的GDOP值作为该只鹰的适应度值,将适应度值最小的鹰作为当前目标组合。

步骤⑤:迭代更新。计算当前猎物能量E,随机生成r,根据值的不同决定采用探索还是不同的开发策略,从而产生新的卫星组合,计算更新后的适应度值,将本次迭代适应度值与原目标组合适应度值比较,将适应度值小的组合作为本次迭代目标组合。不断重复本步骤,直至达到最大迭代次数,当前目标组合即最优卫星组合。

3 HHO选星算法性能分析

针对智能优化算法在多GNSS选星中的应用,参数选择是决定算法性能的关键。在HHO选星算法中,主要影响选星性能的参数为种群规模(鹰的数量)和迭代次数(搜索次数),规模和次数的差异对选星误差和耗时有着较大的影响。

群体智能优化算法是将种群逐渐向真值逼近的算法,但因存在随机性和初始种群选取的差别,每次结果并不一定能够与真值保持一致。因此,为了具象化算法的选星性能,对算法进行了多次蒙特卡罗实验,最后统计出GDOP最大、最小和平均值,最大值表示此时卫星构型最差,最小值表示此时构型最优,平均值则反映了算法的平均选星性能。遍历法的选星结果是最优结果,将遍历法结果与HHO法选星结果比较可以看出HHO法选星的性能。

3.1 鹰群个体数对HHO选星性能的影响

将迭代次数固定为40,鹰群个体数依次设置为20、40、60、80、100,各进行100次蒙特卡罗实验求取均值,分析鹰群个体数对选星性能的影响,结果如图4～图6和表1所示。

图4 种群数引起的GDOP值变化Fig.4 Changes in GDOP value caused by population number

图5 种群数引起的计算耗时变化Fig.5 Changes in calculation time due to population number

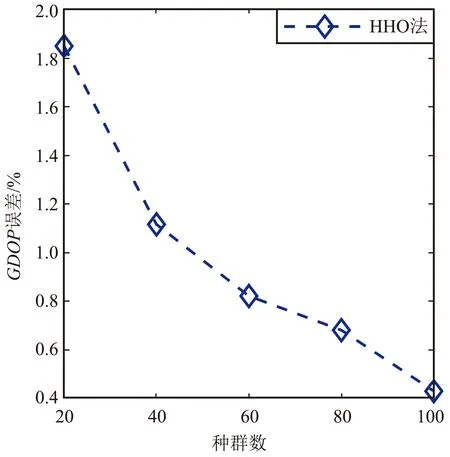
图6 种群数引起的GDOP误差变化Fig.6 Changes in GDOP error due to population number

表1 鹰群个体数对算法性能影响

分析图5和表1的数据可知,增加种群规模也会增加选星算法的耗时,由开始的0.057 1 s逐渐增加到0.279 0 s,但仍旧低于遍历法的耗时。可见HHO选星算法能够实现在保证准确率的前提下快速选出最优构型。

3.2 迭代次数对HHO选星性能的影响

将鹰群个体数固定为40,迭代次数依次设置为20、40、60、80、100,进行同3.1节的实验,结果如图7～图9和表2所示。

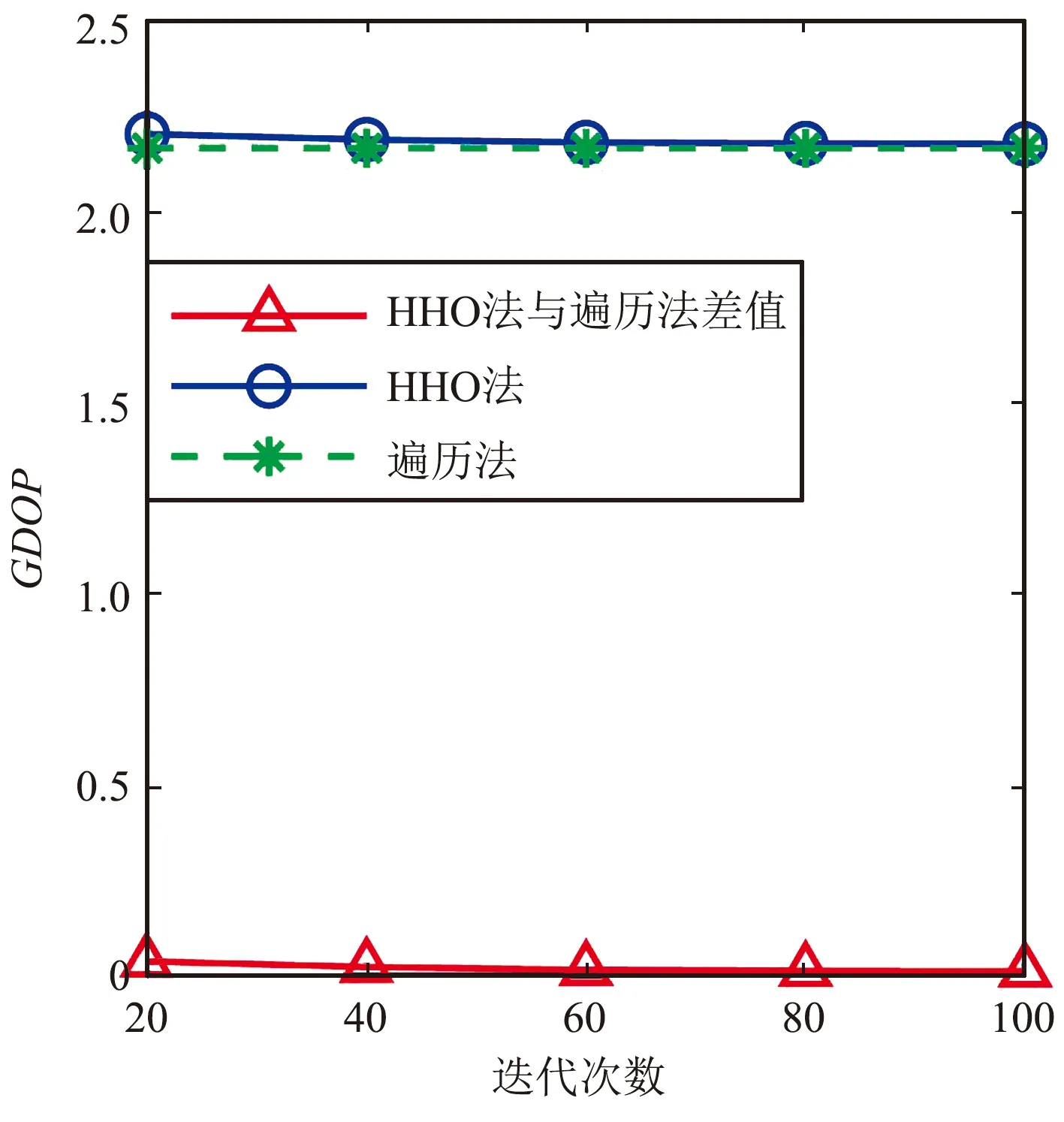
图7 迭代次数引起的GDOP值变化Fig.7 Changes in GDOP values caused by the number of iterations

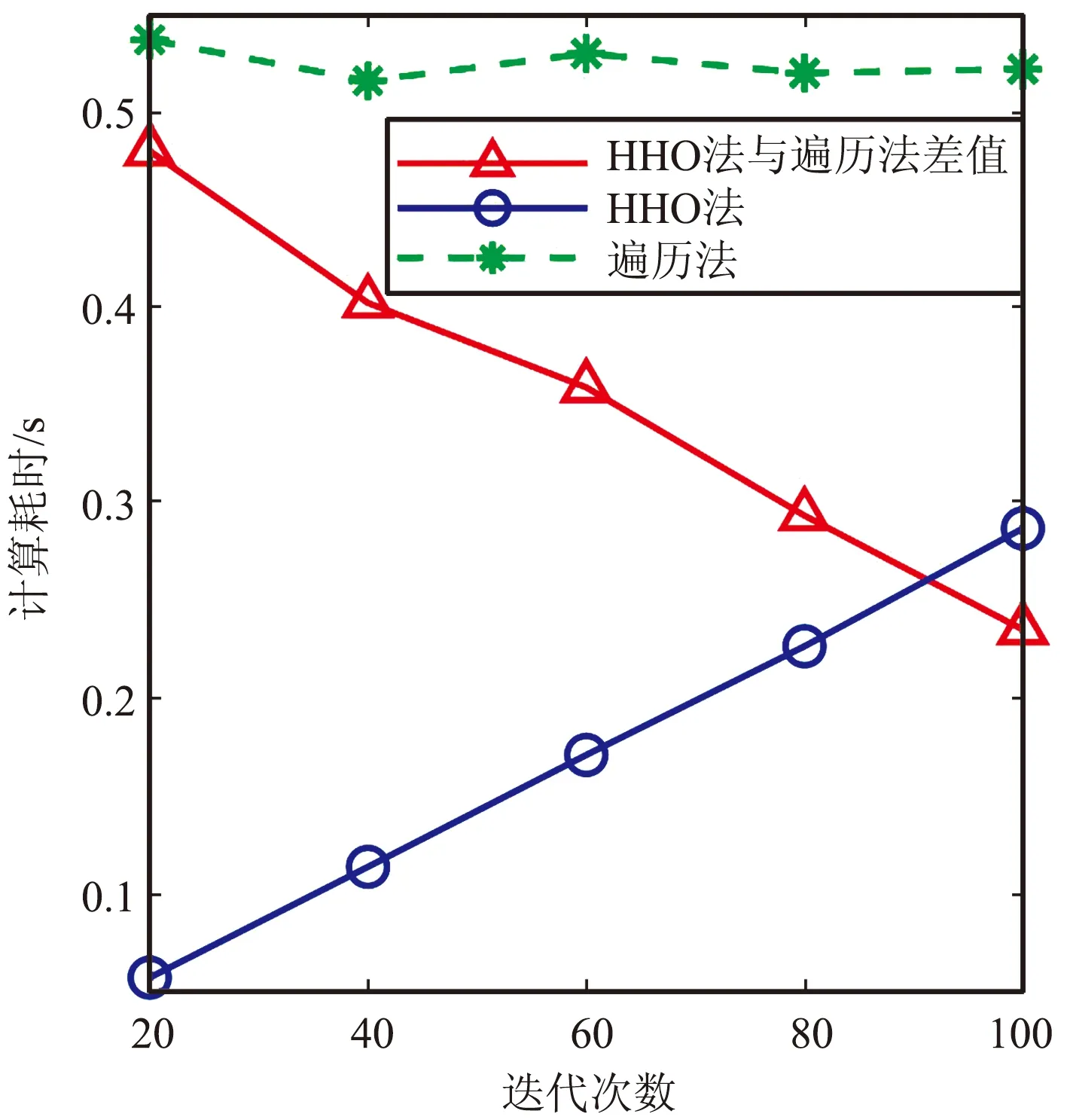
图8 迭代次数引起的计算耗时变化Fig.8 Change in computation time due to the number of iterations

由图7～图9可以看出,随着迭代次数的增加,其选星性能变化类似于种群数对HHO选星性能的影响。在迭代次数增加过程中,选星性能逐渐提高,最终GDOP值逼近遍历法的选星结果,可见,通过增加迭代次数能够有效改善HHO选星算法性能。

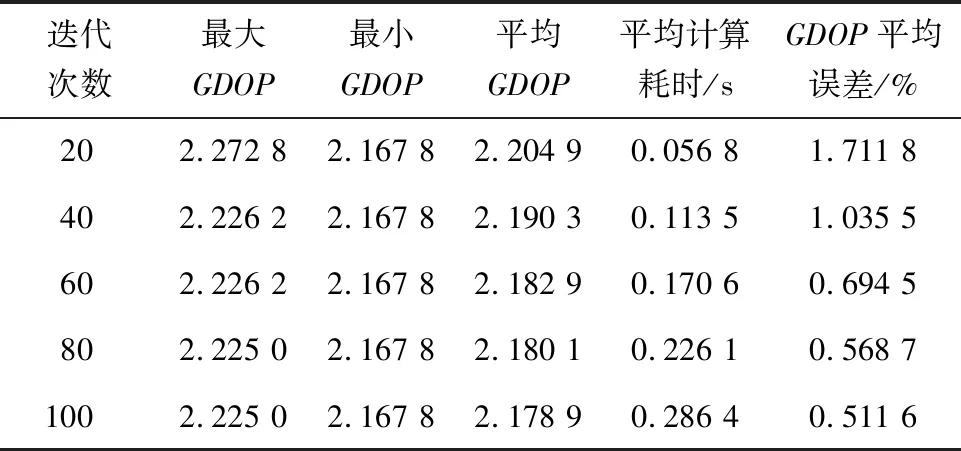
表2 迭代次数对算法性能影响

通过观察表2的数据可以直观地发现迭代次数对HHO选星算法性能的影响。

结合3.1和3.2节的仿真分析可知,种群规模和迭代次数对于HHO选星算法的性能起着关键作用,需要在误差和耗时之间做折中。因此要想最大限度地保证HHO选星的性能,正确地选取种群规模和迭代次数至关重要。由表1可以看出,在种群规模数达到40时,GDOP误差变化不再明显;在表2中,迭代次数在40～60误差变化率为0.341%,而在60～80变化率只有0.125 8%,因此,在迭代次数达到60后误差下降速度不显著。综上所述,在下一节的仿真验证中,采取种群规模数为40、迭代次数为60,以实现在保证选星准确率的前提下尽量降低选星时间。

4 仿真验证与结果分析

在定位前进行选星操作可以从多颗冗余星中选出最优的卫星构型,从而保证定位精度。为了验证HHO算法的选星性能,利用卫星工具包(Satellite Tool Kit,STK)导出BDS、Galileo、GLONASS以及GPS的星历数据,进行仿真分析。仿真所用软件为Matlab 2016b和STK 11.2,计算机搭载CPU处理器(i7-11800H,2.3 GHz)、RAM 32 GB。

实验1:在STK中设置接收机的位置为南京(118.78°,32.10°,0),加入BDS、Galileo、GLONASS和GPS共68颗卫星,起始时间为2022-10-13T04:00:00,导出不同时刻接收机能同时获取的仰角大于5°的卫星星历数据。将选星算法的种群规模设置为40,迭代次数设置为60,选7颗星,仿真时长为90 min,仿真步长为1 min。仿真结果如图10、图11和表3、表4所示。

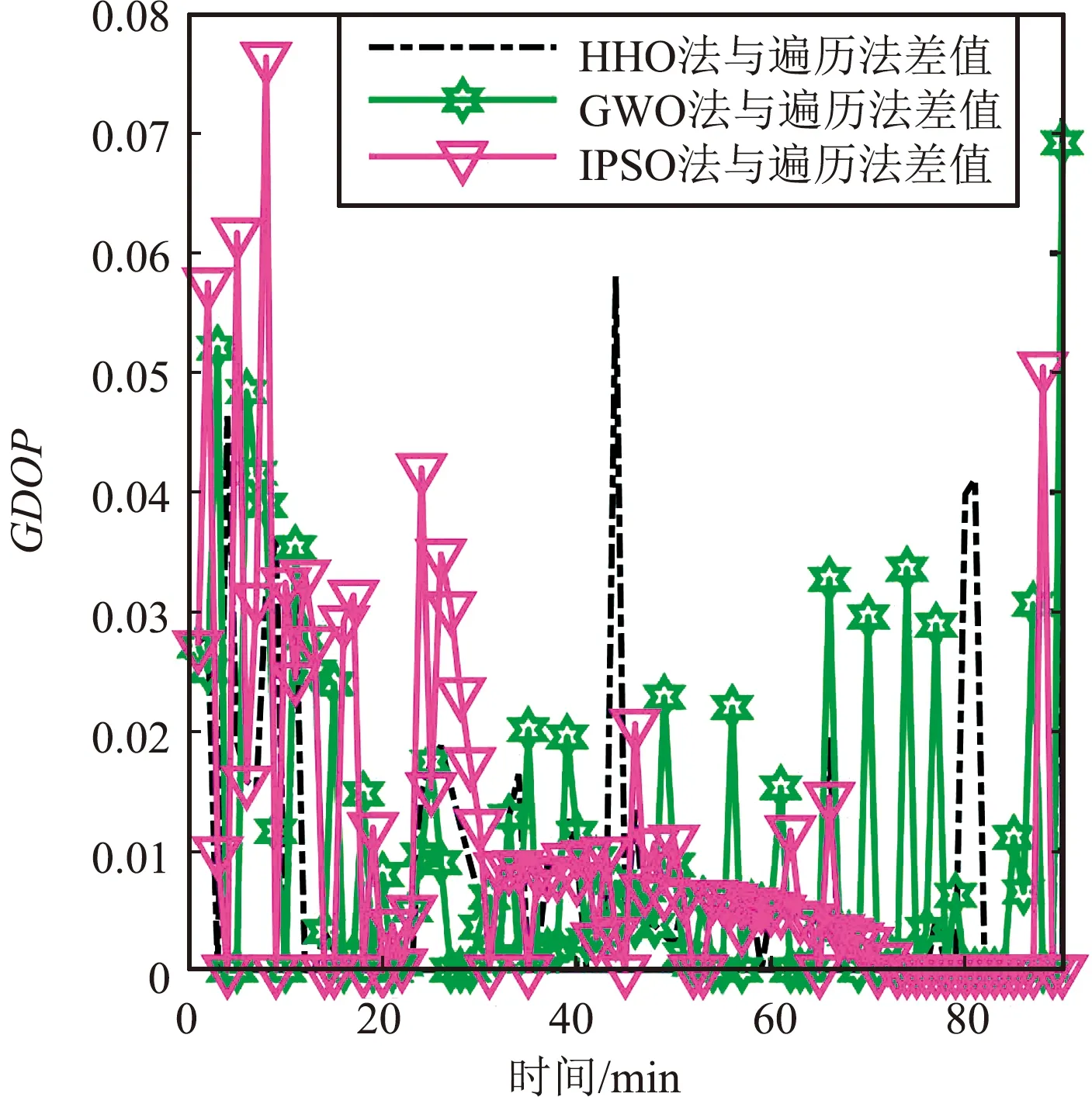
图10 不同选星时间GDOP值误差变化Fig.10 GDOP value error changes at different time of satellite selection

图11 不同选星时间耗时变化Fig.11 Time consuming changes at different time of satellite selection

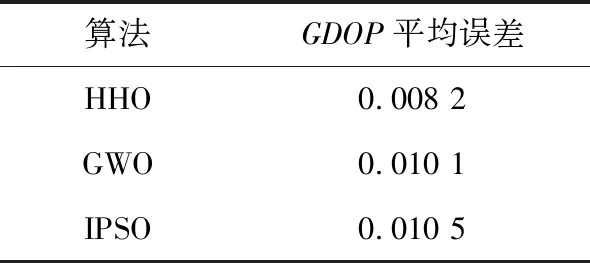
表3 不同算法选星GDOP误差

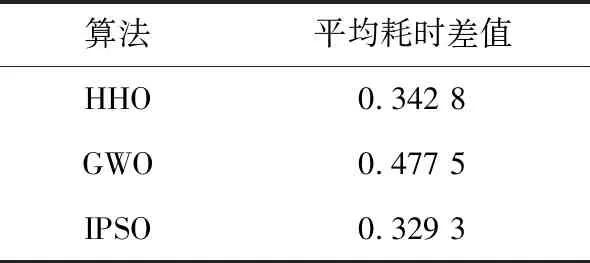
表4 不同算法与遍历法的选星耗时差值

图10和图11分别为不同时刻的HHO法、GWO法、IPSO法和遍历法选星的GDOP和耗时差值。由图10可以看出,在选星的不同时刻,3种优化算法的选星结果均逼近遍历法选星,GDOP误差最大接近0.08,但HHO法选星GDOP误差普遍低于另外2种算法,结合表3不难发现,在90 min内,HHO法选星结果的GDOP平均误差为0.008 2,远低于另外2种优化算法的0.010 1和0.010 5。由图11可以看出,3种优化算法选星与遍历法选星耗时差异较大,选星耗时远低于遍历法选星耗时,其中HHO法选星耗时高于GWO法,低于IPSO法,主要原因是GWO算法实现最为简单,算法的复杂度最低,该算法实现仅需3个阶段:包围猎物、追踪猎物、攻击与搜索猎物,且迭代公式的复杂度较低。而HHO算法虽也分3个阶段,但在第3阶段中需要依据猎物的逃逸风格和哈里斯鹰的追逐策略,从4种策略中选择一种去模拟该阶段,且迭代公式的计算复杂度略高于GWO法。而IPSO法由于引入粒子交叉和淘汰替换机制,复杂度高于HHO法。结合表4数据,GWO法耗时差值最大,为0.477 5 s,其次为HHO法,差值为0.342 8 s,最小值为IPSO算法的0.329 3 s。综上,HHO法耗时虽然略高于结构较为简单的GWO法耗时,但其GDOP误差却远低于另外2种算法,在实际选星过程中性能满足准确率和实时性的要求,能够实现在保证准确率的前提下快速选星。

实验2:采用实验1的参数,进行30次重复实验求均值,仿真HHO法在2022-10-13T04:00:00选择不同卫星数时的选星性能,此时仰角大于5°的可用星有17颗。在BDS/GPS双系统时选5颗星,在BDS/GPS/GLONASS三系统时选6颗星,在BDS/GPS/GLONASS/Galileo四系统时选7、8、9颗星。仿真结果如图12～图15和表5、表6所示。

图12 不同选星数GDOP值变化Fig.12 GDOP value changes with different number of selected satellites

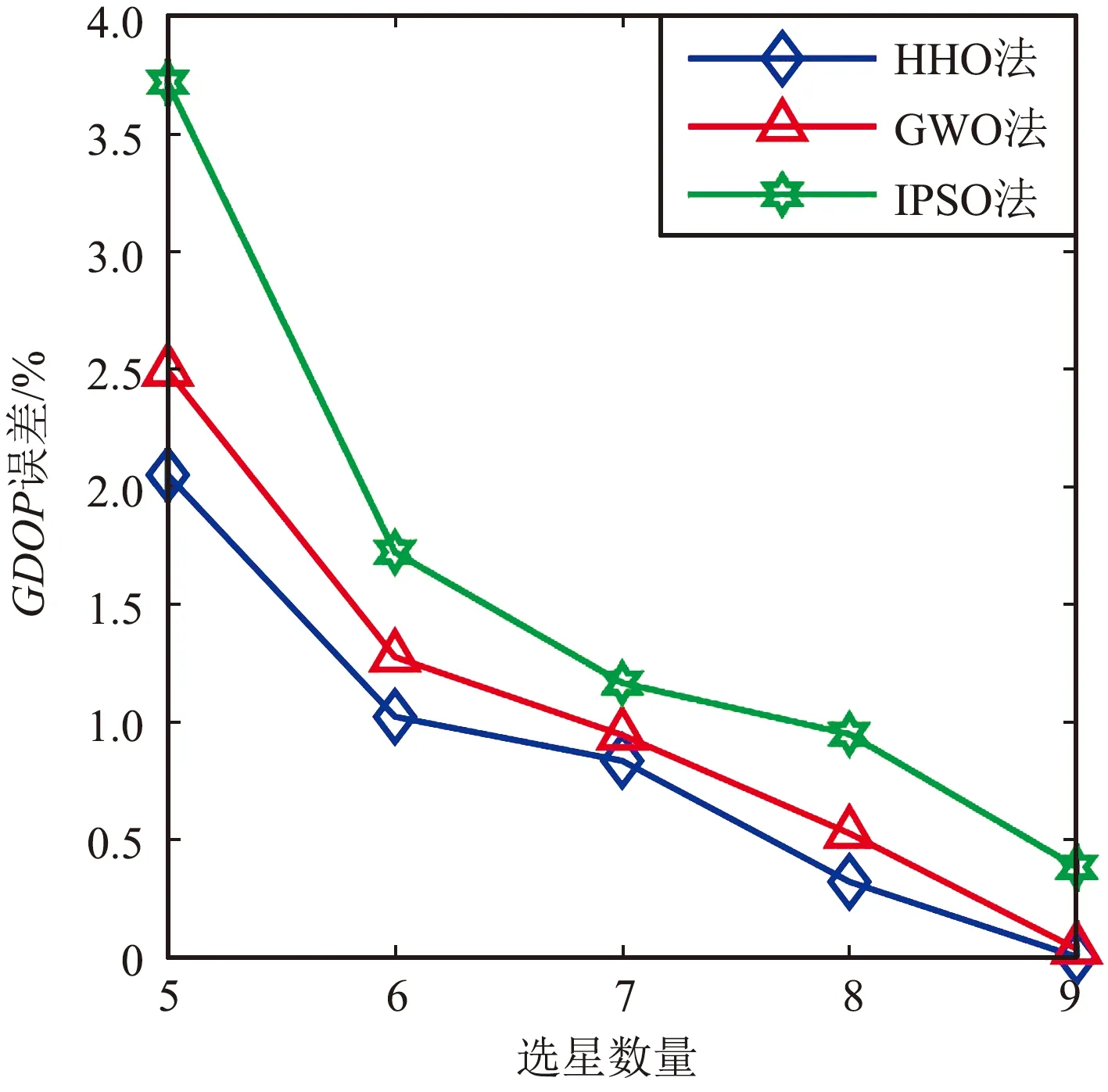
图13 不同选星数GDOP计算误差变化Fig.13 Calculation error variation of GDOP with different number of selected satellites

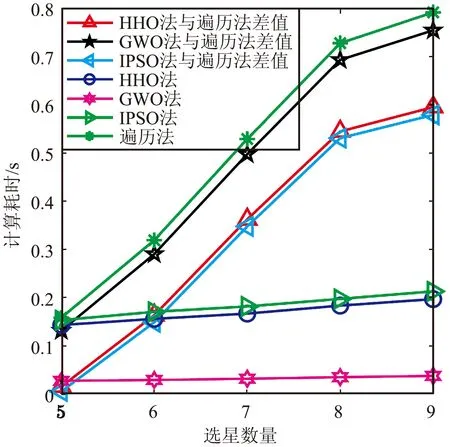
图14 不同选星数耗时变化Fig.14 Time consuming change of different satellite selection number

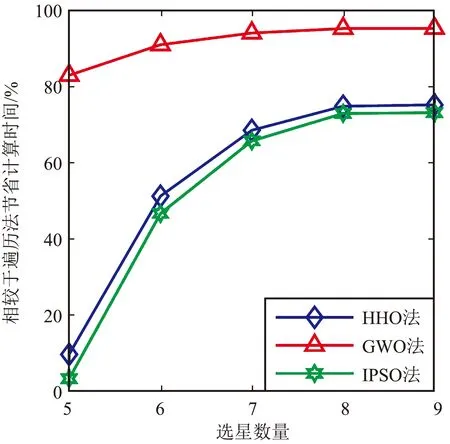
图15 不同选星数节省时间变化Fig.15 Different number of satellites to save time change

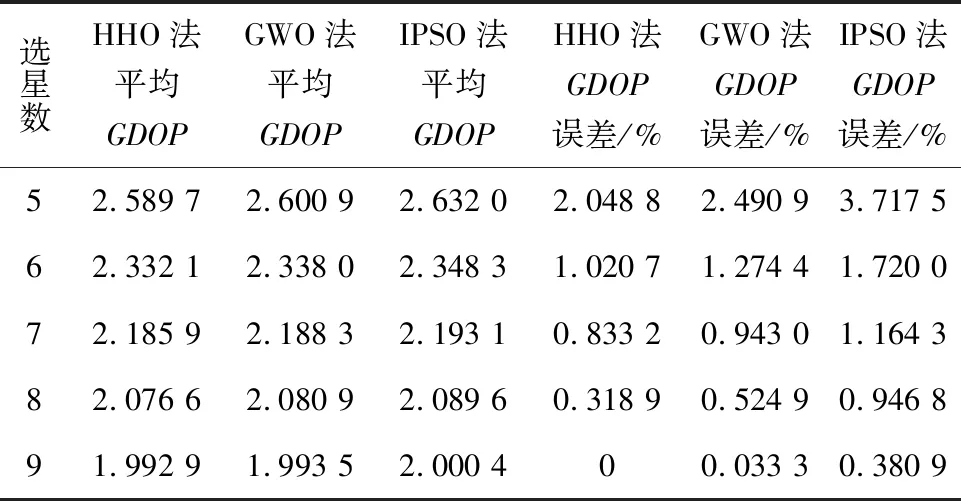
表5 不同选星数选星GDOP值

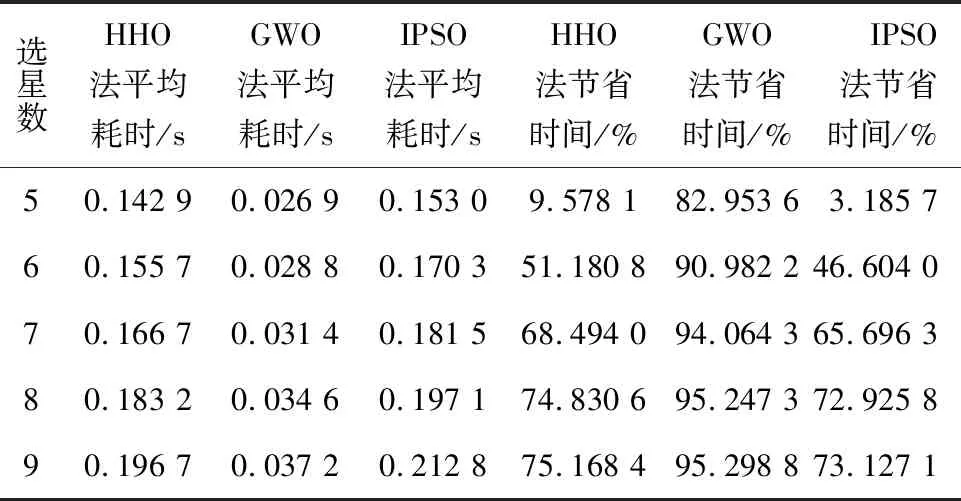
表6 不同选星数选星耗时

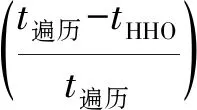
5 结论

本文提出了一种基于HHO的多GNSS星座选星算法,通过Matlab仿真分析验证了算法性能。首先给出了HHO算法的模型;接着将HHO算法引入到选星过程中,以GDOP值作为适应度函数来衡量选星准确率,给出了HHO选星算法的实现步骤;之后考虑了HHO算法的参数设置对选星性能的影响,通过仿真来确定合适参数的选取;最后利用STK导出的卫星星历进行性能验证。结论如下:

① HHO法选星性能受迭代次数和种群数影响,选星准确率与其成正比关系,但选星效率会下降。选取种群规模为40,迭代数为60可以兼顾选星准确率和效率。

② 对STK导出的90 min内数据,利用HHO法、GWO法、IPSO法与遍历法对比,HHO法选星GDOP平均误差为0.008 2,平均耗时差值为0.342 8 s,可见HHO选星性能优异。

③ HHO选星算法对选多星有优势,选星数越多,性能越好,当种群数量为40,迭代次数为60,选星数达到9颗时,HHO选星算法相较于遍历法计算效率提升了75.168 4%,而此时GDOP误差为0。

④ HHO选星算法在实际应用时可根据自身需求,通过改变种群规模数和迭代次数在实时性和准确率之间做取舍。将来的研究将聚焦于自适应选取参数、多算法混合使用和单算法优化等方面,以提高选星性能。