基于SR-FSDAF多源影像融合的内陆水体NH3-N反演研究

马玉荣，柯美如

(1.郑州大学 水利与交通学院，河南 郑州 450001；2.郑州大学 图书馆，河南 郑州 450001)

0 引言

生活与工业废水排放尤其是NH3-N污染物激增,导致了水体发黑发臭和富营养化,严重破坏了河道的生态系统,影响城市居民的生活和健康。传统的NH3-N人工监测方法工作量大、费时费力,难以实现大规模、多时段检测,而遥感技术的快速发展,为河流大范围水质监测提供了技术支持。利用遥感影像监测水体NH3-N浓度的基本原理是基于对水体中不同浓度NH3-N的光谱特征进行分析,选取高相关性波段建立反演模型。龚绍绮等[1]通过实验室NH3-N溶液光谱分析得出氮在404、477 nm波长处相关性最高,对应波长的单波段反演模型的拟合度确定系数(R2)分别为0.976和0.947。段洪涛等[2]利用光谱仪对南湖总氮进行实验,发现最大相关性出现在443 nm处,反演模型R2为0.75。徐良将等[3]利用太湖区域的高光谱数据,用波段比值对水中氨氮浓度进行反演,结果得到波段比值1 015 nm/528 nm与总氮浓度相关性最高为0.803,R2为0.839,这些相关研究为利用遥感影像监测水中氨氮提供了一定依据。

目前,遥感水质监测的卫星数据有MODIS、MERIS[4]、TM/ETM+、Landsat-8 OLI[5-6]、HJ-1 CCD、GF-1[7]、Sentinel-2[8]等,内陆水体NH3-N监测常用的遥感数据有Landsat-7 ETM+、Lamdsat-8[9-10]、SPOT 5[11]等。Landsat-8影像质量优于之前Landsat系列,空间分辨率为30 m,回访周期为16 d,是目前水质监测的重要数据源。而MODIS卫星回访周期为1 d,具有高时间分辨率,但空间分辨率较低,250 m (1～2波段)、500 m (3～7波段)、1 000 m (8～36波段)。Landsat和MODIS影像获取便利,且历史影像丰富,因此Landsat系列被广泛用于内陆水体水质监测,MODIS则多用于海洋监测。

由于大气条件和重访周期的影响,满足定量反演云量要求的中高分辨率卫星时间间隔过大,难以有效获取河道水体污染物浓度的动态变化趋势;MODIS等多光谱卫星时间分辨率虽高,但其空间分辨率较低,难以识别较窄的内陆河道。如何能既准确获取内陆河道信息,又提高反演的时间频率、加强水质污染物的动态监测,是亟待解决的问题。因此,开展多光谱和高空间分辨率影像的融合模型研究,可提高影像的空间分辨率和时间分辨率,为进一步准确、动态反演内陆河道水体的NH3-N浓度提供了保障。

现有时空融合算法根据计算原理的不同分为5类:基于解混的方法、基于权重函数的方法、基于贝叶斯原理的方法、基于学习的方法和混合型方法。基于解混的方法主要有STDFA(Spatial Temporal Data Fusion Approach)[12],其解混误差较大,且缺乏地物的类内变化。基于权重函数的方法如STARFM(Spatial and Temporal Adaptive Reflectance Fusion Model)[13],利用图像信息进行权重分配来估计高分辨像素值,对异质变化无效,且权重函数基于经验获得,缺乏迁移性。基于贝叶斯估计理论的方法[14]自定义输入图像和融合图像间的关系,但函数确立过程复杂且异质表现一般。基于学习的方法使用机器学习建模高分辨率和低分辨率影像之间的映射关系,从而预测融合图像,例如Huang等[15]提出的SPSTFM (Sparse Representation Based Spatio-Temporal Reflectance Fusion Model),其融合结果虽有提升,但学习成本较高、迁移性差,且缺乏光谱原理性支撑。混合型方法整合前4类中2种或多种方法,如王宇恒等[16]将PanSharpening和时空融合进行结合,以获取时、空、谱互补信息。Zhu等[17]提出的FSDAF(Flexible Spatio-Temporal Data Fusion),将解混、加权函数和空间插值方法结合,减少了图像的输入量,对异质变化的预测有所增强,但表现仍不理想,不能满足于更高精度的变化监测。基于此,提出了改进的时空数据融合(SR-FSDAF)模型。利用SR-FSDAF提高监测的频次和中低分辨率图像的利用率,生成高频融合图像,并应用于信阳市水质NH3-N浓度监测,对淮河流域信阳段内的内陆河道进行NH3-N浓度的反演与时空分布变化分析。

1 时空融合模型SR-FSDAF

FSDAF由Zhu等[17]于2016年提出,该方法对地物进行分类,利用不同类型地物在MODIS上体现出的变化,粗略得到每类地物的时间变化值,对预测日期的MODIS影像进行薄板样条采样(TPS),得到粗略的地物空间变化值。TPS基于空间上相关性对数据进行差值重采样,能保留图像的局部变化信息。将2种变化值利用邻域信息赋予不同权重,减少预测结果的偏差,具有更强的稳定性和空间连续性。但FSDAF对于空间突变的预测表现相对无突变情况仍然下降较多。基于FSDAF的思想,对空间突变预测的主要信息源MODIS影像,使用高效亚像素卷积神经网络(Efficient Sub-Pixel Convolutional Neural Network, ESPCN)替代TPS,保留更多的纹理信息,从而提高算法对于空间异质变化的预测精度。

1.1 时空融合模型SR-FSDAF构建

基于超分辨率和灵活时空数据融合模型的SR-FSDAF分为6个步骤:基于无监督分类的MODIS像元纯度计算、像元时间变化粗估计、时间变化残差计算、基于ESPCN的超分辨率空间变化预测图像重构、残差分布计算以及基于邻域信息的增强和融合。为方便描述,将高空间、低时间分辨率的Landsat图像表述为“细分辨率图像”,将高时间、低空间分辨率图像MODIS表述为“粗分辨率图像”,使用t1时刻的Landsat和MODIS影像及t2时刻的MODIS影像预测t2时刻的Landsat影像。算法流程如图1所示,模型的变量及定义如下:

m——一个MODIS像元内对应的Landsat-8影像的像元数;

(xi,yi)——第i个MODIS像元的下标;

i——MODIS的像元下标;

j——在一个MODIS像元中的Landsat-8像元的下标(j=1,2,…,m);

M1(xi,yi,b),M2(xi,yi,b)——在t1和t2时刻MODIS(xi,yi)位置上第b波段的值;

L1(xij,yij,b),L2(xij,yij,b)——在t1和t2时刻MODIS(xi,yi)位置上第j个Landsat-8像元在第b波段的值;

Pc(xi,yi)——第i个MODIS像元中第c类Landsat-8像元所占的比例;

ΔM(xi,yi,b)——第i个MODIS像元在第b波段上t1—t2时刻的变化;

ΔF(c,b)——Landsat-8影像c类地物第b个波段t1-t2时刻的变化,c为水体、农田、建筑物和林地其中之一。

图1 SR-FSDAF模型算法流程Fig.1 Flowchart of SR-FSDAF algorithm

(1)基于无监督分类MODIS像元纯度计算

MODIS影像的空间分辨率为500 m,Landsat影像空间分辨率为30 m。经过图像配准,一个MODIS像元大约与16个Landsat像元覆盖面积相同,基于此对应关系,对t1时刻的Landsat图像进行K-means地物分类,将分类数设置为水体、农田、建筑物和林地4类。通过Landsat像元分属哪几类及各类占比Pc(xi,yi),c=1,2,3,4表示分类之一。

(2)像元时间变化粗估计

基于式(1)计算MODISt1～t2影像反射率变化。

ΔM(xi,yi,b)=Mt2(xi,yi,b)-Mt1(xi,yi,b)。

(1)

根据光谱解混原理[18],ΔM可被表示为式(2),用最小二乘反向求解式(2)可得到ΔF(c,b)。

(2)

(3)时间变化残差计算

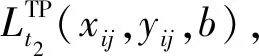
(3)

如果2个时刻之间地物发生了光谱信息的变化,所造成的偏差定义为R(xi,yi,b),计算见式(4),其中n=16。

R(xi,yi,b)=ΔM(xi,yi,b)-

(4)

(4)基于ESPCN超分辨率空间变化预测图像重构

ESPCN是对低分辨率图像卷积的高效超分算法,其通过学习低分辨率影像和高分辨率影像之间的特征映射,恢复空间特征信息。ESPCN的输入为裁剪并重采样至与高分辨率图像大小一致的低分辨率图像和高分辨率图像的图像对数据集。ESPCN将卷积神经网络直接应用于低分辨率图像,利用亚像素卷积将低分辨率特征映射放大。3次卷积后,得到通道数为r2的与输入图像大小一样的特征图,再将特征图像重排列为rH×rW×1的高分辨率图像,具体网络训练参数设置参照文献[19]。

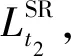
(5)

(5)残差分布计算

将残差R(xi,yi,b)和残差ESR(xij,yij,b)结合,使用4×4移动窗口计算与中心细分辨率像元地物类别一致的像元数和窗口内像元总数的比值I(xij,yij)作为同质性指标。计算见式(6),其中(xij,yij)为中心像元,当窗口内像元类别一致时,Ik的值为1,否则为0。

(6)

计算2个预测结果之间的差值,为残差的差异值ESR-TP(xij,yij,b):

(7)

依据同质性指标I(xij,yij)对预测的细分辨率影像的残差分布进行权重分配,得到权重分布Ew(xij,yij,b),见式(8)。将Ew进行归一化得到归一化残差分布W(xij,yij,b),见式(9)。t2时刻的预测细分辨率像元的残差EL(xij,yij,b),见式(10)。

Ew(xij,yij,b)=ESR-TP(xij,yij,b)×I(xij,yij)+

R(xi,yi,b)×[1-I(xij,yij)],

(8)

(9)

EL(xij,yij,b)=n×R(xi,yi,b)×W(xij,yij,b)。

(10)

t1～t2的细分辨率像元在波段b的像素变化值ΔL(xij,yij,b)计算如下:

ΔL(xij,yij,b)=EL(xij,yij,b)+ΔF(c,b)。

(11)

(6)基于邻域信息的增强和融合

使用邻域信息增加预测稳定性,减少移动窗口的区块效应。对于在t1时刻细分辨率图像像元(xij,yij),选取n个同类且与像元在其邻域内光谱差最小的细像元。第k个细像元与像元的光谱差为Sk,计算如下:

(12)

相似像元对中心像元的贡献权重Dk与距离呈负相关,距离越远,贡献值越少,计算方法见式(13)。归一化处理后,权重wk的计算方法见式(14):

(13)

(14)

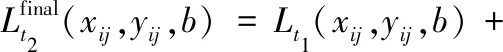
(15)

1.2 模型评价指标

为了比较融合效果的精度和优劣,使用STARFM、FSDAF和SRCNN嵌入FSDAF三种算法作为对比融合模型,分别定性和定量对结果进行分析。定性评价方法通过视觉比较将t2时刻模型融合结果和真实Landsat图像进行对比,得到局部细节的模拟真实程度和整体的色彩差异性是否过大。定量评价方法使用3类评价指标,分别从融合图像的结构整体相似性、反射率还原度和光谱保真度进行综合评价。

结构整体相似性指标为结构相似度(SSIM),被广泛用于评估2张相似图像的线性关系强度,计算如下:

(16)

式中:μx、μy是t2时刻Landsat真实图像和融合的细分辨率图像的平均值,σx、σy是二者的图像方差,C1、C2是用于保证指标计算结果的有理性的非零常数。2幅图像的整体结构越相似,SSIM的值就越接近1。

反射率还原程度的评价指标为均方根误差(RMSE),其反映像素值的还原程度和细节信息的模拟融合结果,计算如下:

(17)

式中:x(i,j)为真实图像,y(i,j)为融合图像。

光谱保真程度使用的评价指标为光谱角(SAM),其将单像素的光谱视为高维向量,计算2幅图像同一位置像素的光谱向量的向量夹角,夹角越小,像素之间的光谱越相似。具体的夹角计算如下:

(18)

2 NH3-N遥感反演模型

2.1 反演模型

特征波段的准确选择是获得高反演精度的基础。利用水质参数NH3-N的实测数据计算和波段组合的相关系数,并选择相关性高的波段或波段组合作为建模参数。

传统的统计回归模型(TSR)已广泛用于水质参数反演,采用一次拟合、二次拟合、对数拟合和指数拟合4类回归函数来构建反演模型,通过对比分析,选择精度最高的一种模型作为后续反演的模型。

2.2 评价指标

反演模型的准确性通过R2、平均绝对百分比误差(MAPE)和RMSE进行评估。MAPE计算如下:

(19)

式中:x为实测数据,y为反演模型的估计值,n为检验的数据数量。

3 研究区域与数据

3.1 研究区域

信阳市(113°45′E～115°55′E,30°23′N～32°27′N)地处河南省南部,面积18 916 km2,地形南高北低,丘陵平原相间,属于亚热带和温带季风气候过渡带以及湿润和半湿润地区过渡带,四季分明,雨热同期。信阳市位于淮河流域,区域内主要支流有浉河、潢河、灌河和史河等。

3.2 实验数据

(1)遥感影像数据

Landsat-8空间分辨率为30 m,回访周期为16 d。MODIS空间分辨率为500 m,回访周期为1 d。MODIS和Landsat具有明显的时间分辨率与空间分辨率差异,且部分光谱波段重合度高,是时空融合算法常用的融合数据源,使用MODIS和Landsat OLI影像进行实验。

时空融合模型的实验数据为信阳市2017年11月8日及11月24日的Landsat图像与MODIS图像对,期间图像没有发生异质突变。NH3-N反演的遥感数据选取云量少于10%且已做过大气校正的Landsat-8 OLI和MODIS日地表反射率数据,影像波段等具体信息如表1和表2所示。

表1 Landsat影像信息

表2 MODIS影像信息

对所选取的Landsat-8 OLI和MODIS数据进行预处理,并将MODIS重投影和重采样至480 m,以便于与空间分辨率为30 m的Landsat影像像素进行匹配和计算。

(2)水质监测数据

实测数据使用2016年9—12月以及2017年2月的信阳区域内信阳市水利局设置的监测站点的实测数据资料,共计773组数据。选取43个监测站点的数据进行实验,站点覆盖信阳市境内淮河主要干支流。

4 实验结果

4.1 不同时空融合模型融合及其对比

将同一时刻的Landsat图像和MODIS图像裁剪至16∶1的大小,将Landsat的B2、B3、B4、B5、B6、B7和MODIS的B3、B4、B1、B2、B6、B7波段按照顺序合成新的多光谱图像,并输入SR-FSDAF模型,得到预测日期的融合图像,融合结果如图2所示。可以看出,SR-FSDAF的局部区域的细节地物捕捉和保留能力更好。

图2 图像融合结果对比Fig.2 Comparison of image fusion results

SR-FSDAF、STRAFM、SRCNN嵌入模型和FSDAF四种融合方法的RMSE、SSIM、SAM的具体值如表3所示,每个波段的最好融合结果值都采用加粗下划线进行突出。分析可知:

(1)光谱保真程度评价指标SAM为图像像素的向量夹角,光谱角越小,像素之间的光谱越相似,图像保真度越高。SR-FSDAF的SAM得到了最优值3.417,说明有着相对最高的光谱保真度。

(2)在Band1上,FSDAF模型的反射率还原程度指标RMSE最小为0.004 5,SSIM也最小为0.982,获得了较好的融合效果。而在Band2～4、Band7上,SR-FADAF模型的RMSE和SSIM获得相对较好的值,和最优值接近。

综合考虑3个指标,SR-FSDAF模型融合影像精度最高,局部区域细节地物捕捉和保留能力更好,计算结果更优。

表3 图像融合精度对比

4.2 基于融合图像的反演

利用信阳市水文局2016年12月5日与2017年1月1日对信阳市重点水功能区布设的43个采样断面采集到的86组水样数据,随机抽取其中62组作为模型训练集用于模型的构建,结合2016年12月7日及2016年12月30日的Landsat与MODIS影像生成的融合影像,分析不同波段和波段组合运算值与NH3-N浓度值之间的Pearson相关系数。共对28个波段的计算值进行了相关性分析,并对相关波段进行了不同组合,具体如表4所示。

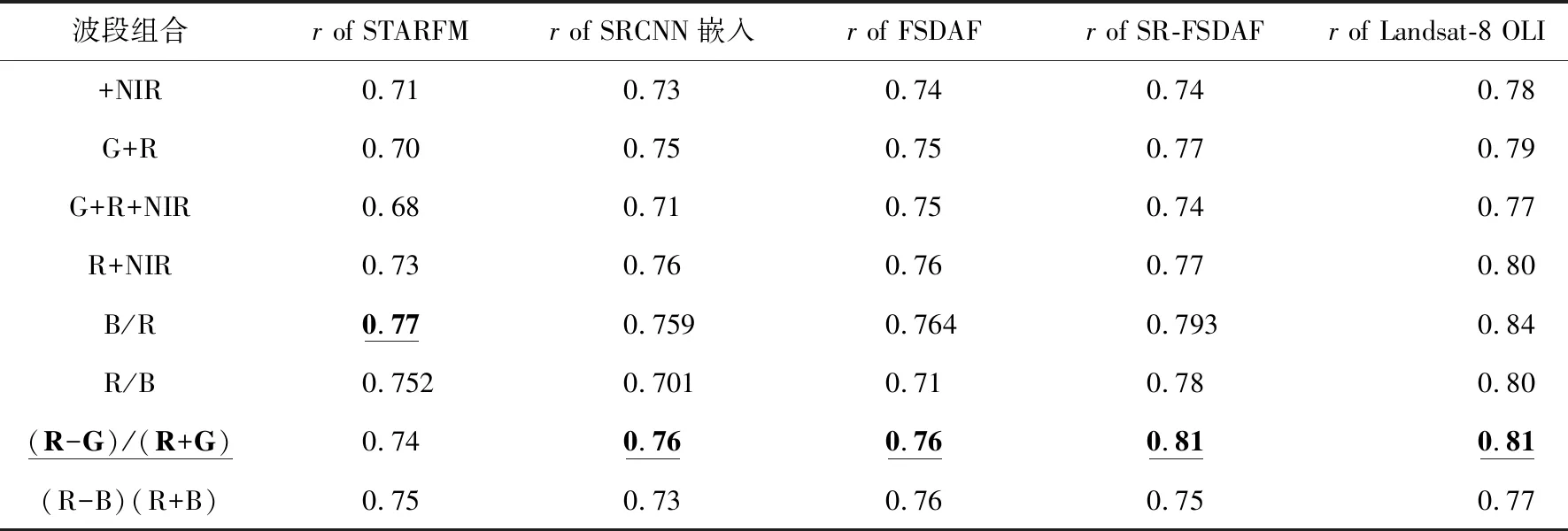
表4 融合影像和Landsat-8 OLI影像波段组合相关性对比Tab.4 Correlation of different band combinations of fused image and Landsat-8 OLI image

28个波段模型中波段组合(R-G)/(R+G)的r值最高为0.805,且为p<0.01,为显著相关。因此最终使用波段组合(R-G)/(R+G)作为NH3-N浓度反演模型的x值。

本文以常见的一次函数、二次函数、指数函数和对数函数4种统计模型作为拟合函数进行反演模型构建,拟合结果如图3～图6所示。

图3 一次函数拟合结果Fig.3 Linear function fitting results

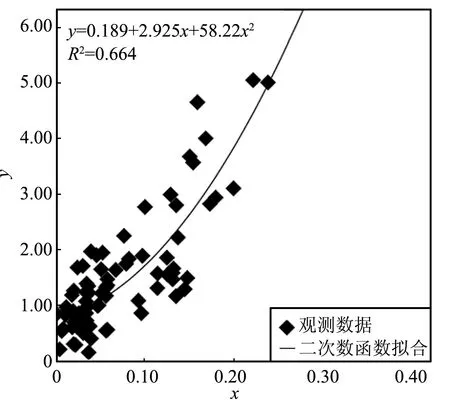
图4 二次函数拟合结果Fig.4 Quadratic function fitting results

图5 对数函数拟合结果Fig.5 Logarithmic function fitting results

图6 指数函数拟合结果Fig.6 Exponential function fitting results

从图中可以看出,二次函数模型不论在浓度高值区还是低值区实际值和函数值拟合度高,整体效果最好,将其作为最终的NH3-N的反演模型,R2为0.664:

(20)

式中:y为NH3-N的估计浓度值。

为验证反演模型在信阳淮河流域的适用性,使用未参与拟合的另外24组实测站点的数据与反演模型的结果进行对比验证,利用MAPE与RMSE进行定量精度评定,总体二次回归的NH3-N的浓度反演模型的平均相对误差为12.37%,RMSE计算结果为0.065 6,满足反演需要的精度要求,以此为基础可展开较为可靠的进一步研究。实测数据和模型预测数据具体如表5所示。

表5 实测数据与模型预测结果对比Tab.5 Comparison between measured data and model prediction results

4.3 不同时期NH3-N浓度整体水平

根据相关调查资料[20],淮河水系每年的7—8月为丰水期,每年12月—次年2月为枯水期,其他月份为平水期。

不同时期(由于丰水期影响,将3—6月和9—11月看作平水期的2个不同阶段进行分析,分别表述为平水期Ⅰ和平水期Ⅱ)的水体NH3-N浓度类别占比变化如图7所示。可以看出,整体上2017年NH3-N浓度呈现略微下降趋势,并具有明显的季节特征。枯水期、平水期Ⅰ、丰水期和平水期Ⅱ的NH3-N浓度平均值为0.753、0.706、0.533、0.544 mg/L。整体趋势为:丰水期<平水期<枯水期。

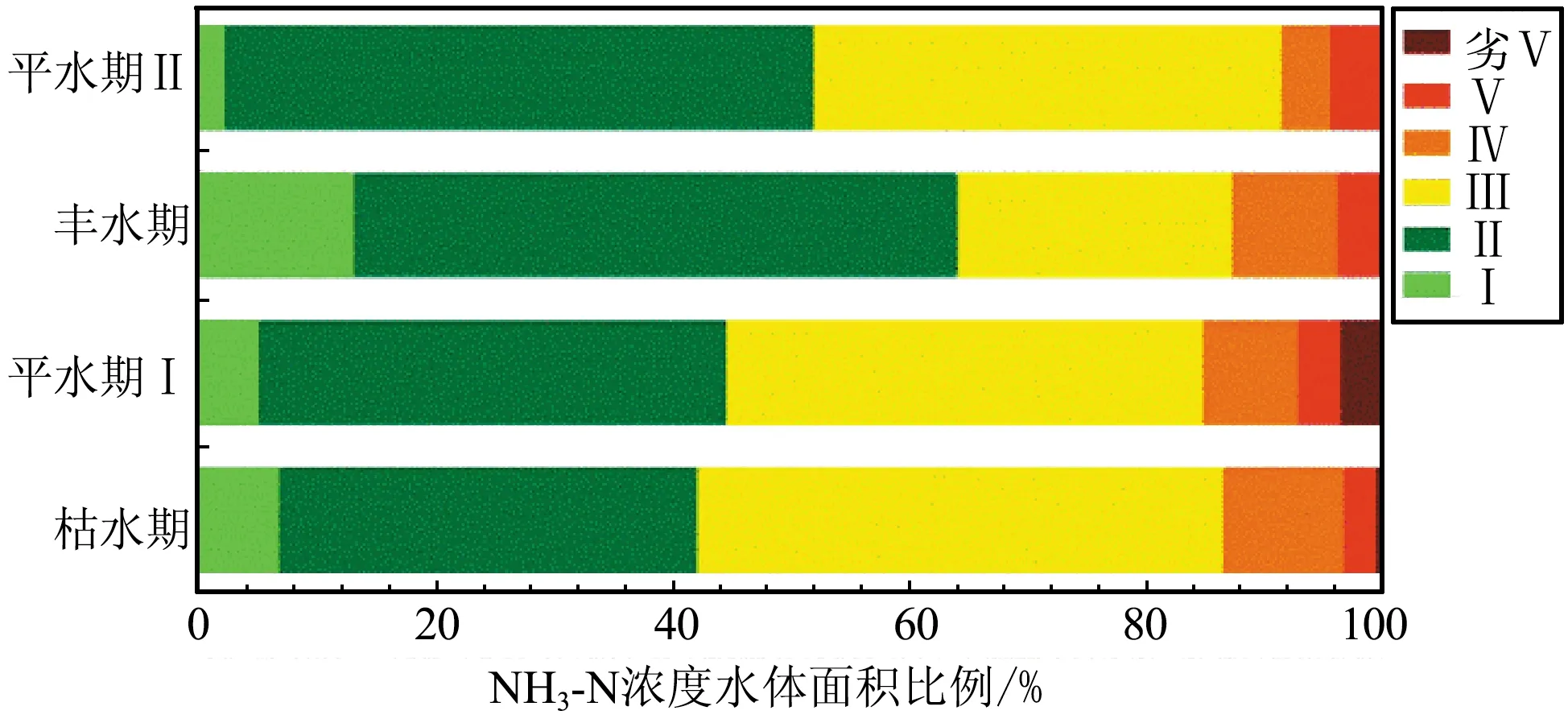
图7 不同水期NH3-N浓度水体面积比例Fig.7 Proportion of water area with NH3-N concentration in different water periods

丰水期时期NH3-N浓度对应标定的6类水的水面积平均占比分别为:13.89%、54.26%、24.6%、9.56%、3.73%、0.31%,水体主要成分为Ⅱ类NH3-N浓度水,水质情况相对较好。丰水期的NH3-N浓度相对最低,变化趋势平缓。

平水期的NH3-N浓度扰动较大,3—6月的平水期前期受枯水期的影响,NH3-N浓度相对较高,9—11月的平水期后期受到丰水期的影响,NH3-N浓度相对较低。

在枯水期,NH3-N浓度最高,高于丰水期和平水期,且变化平缓。枯水期间NH3-N相对浓度最低为12月,主要为Ⅱ类水和Ⅲ类水,占比达到82.77%,从12—次年2月NH3-N浓度逐渐上升,在1月劣Ⅴ类NH3-N浓度水的比例有所增加,出现在竹竿河的部分区域;2月Ⅴ类NH3-N浓度水面积增长较多,主要出现在小潢河和浉河以及灌河下游。枯水期Ⅰ类NH3-N浓度水占总水面平均面积为6.69%,Ⅱ类NH3-N浓度水占整体面积的35.41%,Ⅲ类NH3-N浓度水的平均占比为44.44%,Ⅳ类NH3-N浓度水的平均面积占比为10.15%,Ⅴ类为2.76%,劣Ⅴ类为0.54%主要出现在个别小支流。

淮河流域信阳段的NH3-N浓度在春季浓度最高,主要是冬季枯水期河流水量少且流速缓慢,NH3-N污染物易产生累积造成的,其浓度均值从0.77 mg/L上升至0.81 mg/L。随着水量增加,NH3-N浓度在5—6月开始下降,并在7—9月的夏季时期因雨季NH3-N浓度全年浓度最低,浓度均值下降至0.52 mg/L。10—12月进入冬季枯水期,NH3-N浓度又缓慢攀升,12月浓度均值为0.69 mg/L。

4.4 重点区域NH3-N浓度分布

依据局部NH3-N浓度差异程度的不同,NH3-N浓度较高的局部小区域主要出现在潢河和浉河的下游。

浉河NH3-N浓度局部长期在1.6～2.3 mg/L,8月时最大值达到了4.5 mg/L,一年内NH3-N浓度变化情况如图8所示。

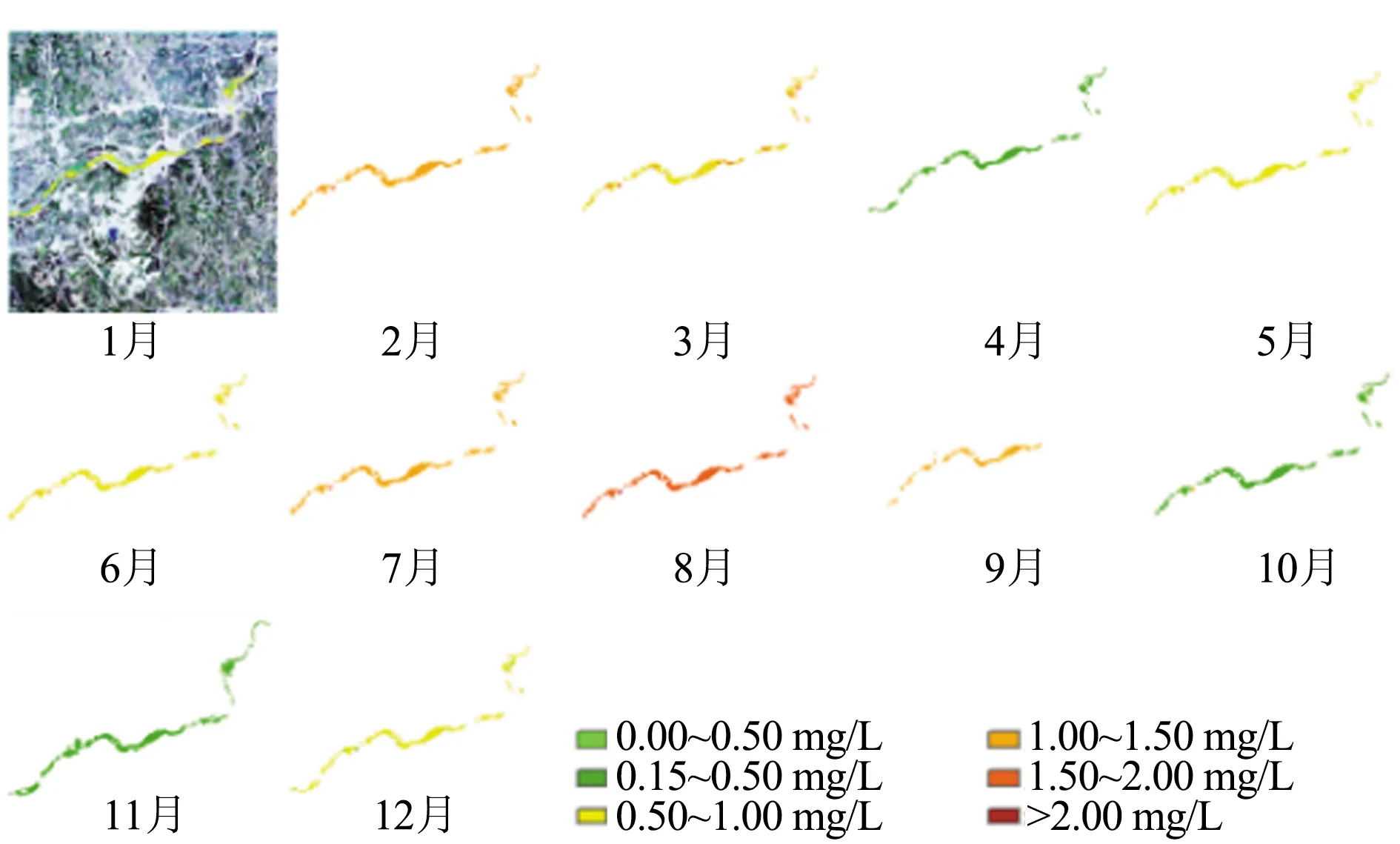
图8 浉河局部区域NH3-N浓度变化Fig.8 Variation of NH3-N concentration in local area of the Shihe River

潢河NH3-N浓度为0.1～1.9 mg/L,小潢河浓度为0.3～2.5 mg/L,且浓度在1.5 mg/L区域基本集中在中下游段,与季节变化趋势相关弱,一年内NH3-N浓度变化情况如图9所示。

图9 潢河局部区域NH3-N浓度变化Fig.9 Variation of NH3-N concentration in local area of the Huanghe River

根据调查,信阳市主要河流周边大部分为农田,市内主要排污口分布在浉河和潢河的工业生产区和生活区,其面源污染主要受农业农田影响,局部V类及以上的严重污染主要受人类工业活动影响。

在丰水期,由于被雨水稀释,NH3-N整体浓度更低;枯水期NH3-N浓度最高,浓度变化平缓;除去排污的影响,在3—9月的农业生产期,农田肥料等污染会造成水体的NH3-N浓度上升和局部变化。对于浉河、潢河等污染物浓度异于季节规律且常有高浓度NH3-N分布的情况,则主要是由工业生产引起的。

5 结束语

提出了改进的SR-FSDAF模型,通过不同融合模型融合结果对比,发现SR-FSDAF模型比STARFM、SRCNN嵌入模型和FSDAF具有更优的视觉效果和指标结果,图像RMSE、SSIM和SAM分别为0.009 9(均值)、0.975 (均值)和3.417。基于SR-FSDAF方法,利用Landsat-8 OLI和MODIS进行时空影像融合,并进行了NH3-N浓度的反演及其时空分析,在一定程度上弥补了传统水质监测方法获得NH3-N污染物时空变化特征难的问题。

提出的SR-FSDAF方法在提高NH3-N浓度反演频率上具有一定参考价值,但仍需随季节性差异和区域性差异进行调整和改进,可为小区域水质监测提供模型与参考。