基坑开挖诱发下卧既有隧道隆起变形解析解

冯国辉 ，陈光仔，张迪，孙峰，万鹏，李雨杰，杨颖，徐长节,

(1.浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058；2.浙江大学 平衡建筑研究中心，浙江 杭州 310028；3.浙大城市学院 土木工程系，浙江 杭州 310015；4.中铁第四勘察设计院集团有限公司，湖北 武汉 430061；5.安徽大学 计算机科学与技术学院，安徽 合肥 230601；6.华东交通大学 江西省岩土工程基础设施安全与控制重点实验室，江西 南昌 330013；7.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013)

城市地下空间的发展越来越受到人们的青睐，近些年来，城市地铁的快速发展极大地改善了城市交通拥堵状况，但其安全性也不容忽视。城市里地下空间的开挖势必会对附近既有线产生较大的不利影响[1-5]。相较于有限元模拟[6-7]和离心机实验[8-10]，理论解析方法拥有简单方便、快速运算的优点，被广泛应用于预测地下建筑物的应力应变。ZHANG 等[11]基于Mindlin 解和Winkler 地基模型提出了基坑开挖诱发下卧隧道隆起变形的简化计算方法；LIANG等[12]将隧道简化成欧拉梁搁置在Pasternak 地基模型上，采用差分法解析获得隧道变形响应应答；康成等[13]考虑到土体弹性刚度非线性情况下隧道隆起变形的简化计算；ZHANG 等[14]将既有管线埋置在非均质土体中，基于Pasternak 地基模型解析获得既有管线在邻近基坑开挖作用下的变形响应解答。为了进一步考虑隧道管片间的剪切变形，梁荣柱等[15-16]将隧道简化成铁木辛柯梁放置在单参数Winkler 和双参数Pasternak 地基模型上，通过两阶段分析法得到隧道变形响应解析。LIU 等[17]从实际工程出发，采用双参数Vlasov 地基模拟隧-土相互作用，阐述了在基坑与隧道竖向净距非常近的情况下，考虑隧道侧向土体影响对预测隧道变形响应可明显提高预测精度。江杰等[18]采用Pasternak 地基和欧拉梁获得层状地基下基坑卸载诱发既有隧道隆起变形解析。然而由螺栓连接相邻管片形成的地铁隧道无法忽略隧道的剪切变形对隧道受力变形的影响[19]。同样的，多位学者采用可考虑土体应力扩散的Kerr地基模型模拟隧道-土相互作用，冯国辉等[20-24]均指出Kerr地基模型计算结果与实测数据吻合较好。综上所述，目前的理论方法缺乏考虑土体应力扩散效应对既有隧道受力变形的影响，基于此，本文在既有研究的基础上提出一种新的解析方法，将隧道所受到的附加应力转化成Fourier 级数，将隧道假定为放置在三参数Kerr 地基模型上的铁木辛柯梁，进一步解析获得基坑开挖诱发邻近下卧隧道变形响应解答，并通过本文解析结果与既有工程案例进行对比验证。随后针对既有工程实况进行参数分析。

1 分析方法

1.1 隧道附加应力计算

矩形基坑与下卧隧道位置简化如图1所示。基坑长、宽及深度分别为L1，B1和H1，既有隧道轴线距离地表深度z0。同时，分别以基坑中点o′和隧道中心点o为原点建立2 个不同坐标系ɛo′η和xoy，其中o′o=d0，且2个坐标系成夹角θ。

图1 基坑与下卧隧道位置关系Fig.1 Correlation position between existing tunnel and excavation

假设均匀分布在基坑底部的卸载为psdɛdŋ(ps=γsH1，γs表示基坑土天然重度)，根据既有文献计算基坑开挖引起下卧隧道轴线处的附加应力[12-13,15-16,21,24]，那么由Mindlin 解可知下卧隧道中轴线任意点(x,0,z0)的竖向附加应力q为[12]：

式中：υ为土体泊松比，且

基于大多数工况中隧道轴线与基坑边缘非平行关系，此时需将2个坐标系进行转换[12]，则有：

1.2 隧道变形理论推导

图2 为基坑开挖诱发既有隧道变形计算简图，并采用Kerr地基模型模拟隧-土相互作用。

图2 Kerr地基模型Fig.2 Kerr foundation model

基于前人的研究[22,24]，可知搁置在Kerr 地基模型上的隧道竖向位移控制方程为：

式中：w2为第2 层弹簧竖向位移，c和k分别为模型中第1 层和第2 层弹簧的地基反力，Gp为地基土体间的剪切效应，D为隧道直径，EI和ϕ分别为隧道抗弯及剪切刚度。

式(4)的齐次方程的形式为：

式(5)可化简为：

式中：χ1，χ2和χ3满足以下条件：

根据文献[22]可知，6阶齐次方程的根为

其中：α和β可由χ2和χ3来确定。

考虑到将隧道简化成无限长梁(-L≤x≤L)，此时基坑开挖引起隧道轴线处的附加应力q(x)可简化成傅里叶级数来表达：

那么控制方程(4)的近似解为：

式中：b1，b2，b3，b4，b5和b6可由隧道两端的边界条件确定，将式(9)～(11)代入式(4)，可得an为

此时，地基剪切层变形量w2的各阶导数数学表达式为

式中：b7～b21可表示为：

由既有文献可知，此时隧道首尾两端可假定成自由[12-13,15,21,24]，即

此时，s1～s10可由b1～b26唯一数学表达，而b7～b26是由b1～b6唯一数学表达。式(17)可表示为：

式中：{b}={b1,b2,b3,b4,b5,b6}T，{R}={R1,R2,R3,R4,R5,R6}T，Kij(i=1…6,j=1…6)是矩阵[K]的子项，可由式(18)得到：

至此，参数b1,b2,b3,b4,b5和b6可由式(18)获得，下层弹簧位移w2(x)可由式(19)获得，进一步隧道的隆起变形w(x)。值得注意的是，当模型中弹簧地基反力c=0时，可得退化的双参数Pasternak地基解[24](T-P 法)；同样的，当铁木辛柯梁剪切刚度ϕ=∞时，可得退化的欧拉梁解(EB-K法)。

1.3 Kerr地基参数确定

依据既有文献[25]，传统的Kerr地基参数确定较为简单：

式中：Et为土体弹性模量。然而，传统方法引入较多假设，缺乏考虑工程实况。冯国辉等[24,26-27]基于本工况采用数值模拟分析比较，获得了Kerr 地基修正基床系数：

2 算例验证

为了验证本文所提出方法的正确性，笔者收集到相关工程已有文献中的有限元数据[12]和上海某隧道工程[6]的实测数据，将收集到的有效数据与本文方法进行对比分析。

2.1 三维有限元数据对比

为了研究邻近基坑开挖对下卧隧道的受力变形分析，LIANG 等[12]基于PLAXIS 3D 软件建模研究了基坑开挖对下卧既有隧道的影响。基坑可简化成矩形，基坑长、宽均为8 m，深6 m。为了消除边界条件对三维模型的影响，设置三维模型的尺寸为200 m×200 m×40 m。基坑模型中，为了抵抗水平土压力的作用，LIANG等[12]设置了4个地下连续墙，每个连续墙的长度为10 m。模型中的土体简化成各向同性的弹性体，均质土体中土的重度为18 kN/m3，隧道位于基坑的正下方且隧道与基坑长边平行。根据志波由纪夫等[28-29]分别计算隧道的抗弯刚度及剪切刚度，具体隧道及土体相关参数信息见表1。

表1 工程实例1计算参数Table 1 Calculated parameters of actual project 1

图3为基于本文方法计算结果、本文退化解析T-P 法、本文退化解析EB-K 法和有限元给出的基坑开挖引起下卧隧道隆起位移图。由图3 可见，4种不同计算方法获得的隧道隆起位移趋势均具有较好的一致性。相比于有限元的计算结果，本文方法得到的隧道最大隆起变形预测解略小，这主要归因于随着基坑的逐步开挖，基坑底部土体卸载导致隧道-土体刚度不断降低，但本文解难以考虑土体刚度削弱的影响，进而引起本文解析结果偏小。从图3 中可以看出，本文方法退化解EB-K法解析获得的计算结果会更加低估隧道的隆起变形，这是由于欧拉梁没有考虑到隧道剪切刚度的因素，致使隧道刚度相比于实际工况会有所偏大，隧道在同样外力作用下抵抗变形的能力会增大。

图3 隧道隆起位移计算及有限元结果对比图Fig.3 Comparison of the calculated and finite element results of uplift deflection of tunnel

2.2 上海某隧道工程

黄宏伟等[6]曾报道过上海某隧道工程的工况，并建立相应的有限元模型模拟研究该工况下隧道变形响应。基坑可简化成近矩形平面，长、宽和深为50 m×10 m×11 m。北线隧道外径11 m，衬砌厚55 cm，开挖基坑平面的长边与北线隧道轴线的夹角为75°。考虑到隧道轴线埋深20.8 m，基坑底部与隧道拱顶均在粉质土层中，地基土弹性模量可取30.8 MPa。梁荣柱等[15]根据志波由纪夫等[28-29]研究可分别计算隧道的抗弯刚度及剪切刚度，具体隧道及土体相关参数信息见表2。黄宏伟等[6]基于现场工况将有限元软件模拟结果与北线隧道现场实测数据进行了对比，为了消除边界条件对三维模型的影响，设置三维模型的尺寸为230 m×150 m×64 m，三维模型划分网格后包含90 000 个结点单元。三维模型四周边界采取水平方向位移约束，底部同时采取水平与竖直方向位移约束。梁荣柱等[15]将北线隧道简化成铁木辛柯梁搁置在Winkler 地基模型上，并比较了解析计算结果与现场实测数据。在此，本文以此隧道工程参数为基础进行算例分析。

表2 工程实例2计算参数Table 2 Calculated parameters of actual project 2

图4 为基于本文方法计算结果、黄宏伟等[6]和梁荣柱等[15]以及工程实测给出的基坑开挖引起下卧隧道隆起的隆起变形图。由图4 可见，3 种不同计算方法获得的隧道隆起变形与实测结果对比均具有较好的一致性。虽然本文方法得到的隧道最大位移预测解略小于黄宏伟等[6]的有限元计算结果，这主要归因于随着基坑开挖深度不断增大，坑底土体的卸载导致隧道-土体刚度不断降低，显然本文解难以考虑土体刚度削弱的影响。然而，梁荣柱等[15]提出的Winkler 地基模型计算结果会高估隧道的隆起变形，这是由于Winkler 地基模型不能考虑到土体的剪切作用，而土体的剪切作用在预测土与结构相互作用时是不可忽略的。从图中还可以看出本文解和有限元结果均稍大于实测结果的最大值，造成这一偏差的原因在计算时难以准确把握工程施工过程中土体参数变化，致使理论计算结果偏大。

图4 隧道隆起位移计算、有限元及实测数据对比Fig.4 Comparison of the calculated，finite element and measured results of uplift deflection of tunnel

3 参数分析

为了研究隧道剪切刚度、土体弹性模量和隧道轴线埋深变化对既有隧道受力变形的影响，以上海某隧道工程的基本工况为基本参数，并采取控制变量法进行参数分析。

3.1 隧道剪切刚度

取6 组不同的隧道剪切刚度进行分析，取ϕ=ts(ϕ)eq，其中ts=0.1，0.2，0.5，1，5，10 且(ϕ)eq为原上海工程中隧道剪切刚度，并通过本文方法获得隧道受力变形响应。

由图5(a)可知，隧道位移会随着剪切刚度的增大而不断减小。同样的，由图5(b)可知，隧道剪切刚度不断增加时，隧道最大变形量逐渐减小，同时其衰减速率逐步下降。这是由于隧道抗力随剪切刚度的增大而不断增强，待隧道刚度增大到一定的程度时，隧道剪切刚度的变化对隧道最大变形位移不再敏感，这也符合前人的研究结果[16]。

图5 不同隧道剪切刚度下隧道受力变形变化Fig.5 Tunnel stress and deflection variation in different tunnel shear stiffness condition

3.2 土体弹性模量

取5组不同的土体弹性模量进行分析，分别为Es=5，10，20，40 和80 MPa。在此参数分析中，采用本文方法以及可退化的Pasternak地基模型(T-P法)获得隧道受力变形响应。

图6为土体弹性模量变化引起隧道最大竖向变形wmax和弯矩Mmax变化曲线。本文方法计算结果显示，随着土体弹性模量从5 MPa 逐渐增大到80 MPa，隧道的最大变形位移从35.1 mm逐渐减小到4.0 mm，降幅接近89%，但其减速是不断减缓的；弯矩峰值从23.5 MN∙m逐渐减小到7.1 MN∙m，降幅接近70%，其降幅速度也在逐渐减小。这是由于随着土体弹性模量的增加，隧道所受附加应力逐渐减小，显然隧道变形及其内力均逐步减小。当采用退化解T-P 法时，隧道变形及其内力变化和本文方法的分析结果基本相同。从图6 可以看出，土体弹性模量越小，退化解与本文解峰值的差值越大，考虑到软土地区土体弹性模量普遍偏小，故采用本文方法对相应工程中隧道变形及其内力的预测更为合理。

图6 不同土体模量变下隧道受力变形变化Fig.6 Tunnel stress and deflection variation in different elastic model condition

3.3 隧道埋深

取5 组不同隧道轴线埋深，即z0=18，20，22，24，26 m。考虑到欧拉梁与铁木辛柯梁计算结果的差别，在此次参数分析中，采用本文方法以及可退化的欧拉梁(EB-K 法)获得隧道受力变形响应。

图7 为隧道埋深变化引起隧道最大竖向变形wmax和弯矩Mmax变化曲线。本文方法计算结果显示，随着隧道埋深从18 m 逐渐增大到26 m，隧道的最大变形位移从12.8 mm 逐渐减小到9.4 mm，降幅接近27%，且其减速基本不变；弯矩峰值从12.0 MN ∙m 逐渐减小到7.0 MN ∙m，降幅接近42%，其速率基本不变。这是由于隧道和基坑竖向净距越大，隧道收到开挖的影响越小。退化解E-K法计算结果趋势和本文方法一致，但退化解将低估隧道的变形但会高估隧道的内力，这是由于欧拉梁将梁体的剪切变形视为无穷大，此时欧拉梁抵抗变形能力增强，同样附加应力下梁体变形就会减小，而梁体所受内力会逐步增强。

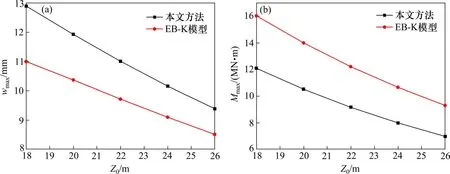
图7 不同隧道埋深变化下隧道受力变形变化Fig.7 Tunnel stress and deflection variation in different depth of tunnel

4 结论

1) 将基坑卸载作用下诱发既有隧道位置处的附加应力转化成Fourier 级数附加在既有隧道上，将隧道假定为放置在Kerr 地基模型上的铁木辛柯梁，结合隧道边界条件得到隧道隆起变形解析方法。

2) 与有限元模拟数据及现场监测数据对比，本方法解析结果均具有较好的一致性。与既有研究解析及退化解T-P 计算结果对比，本方法预测结果更贴近实测数据。

3) 参数分析结果表明：隧道变形会随剪切刚度增大而不断减小，但隧道所受弯矩和剪力会随之不断增大；土体弹性模量和隧道埋深的增大均会引起隧道变形以及弯矩和剪力不断减小。相比于本文可退化的T-P 法，本文方法会低估隧道变形及其内力；相比于本文方法，本文可退化的E-K法计算结果将低估隧道变形，但会高估隧道内力的大小。