地震作用对中速磁浮列车-轨道-桥梁系统耦合振动的影响研究

唐昊天，黄凤华，滕念管

(1.上海交通大学 船舶海洋与建筑工程学院，上海 200240；2.南京工业大学 土木工程学院，江苏 南京 211816)

磁浮交通因具有噪声低、污染小、线路适应性强以及维护成本低等显著优点，越来越受到人们的欢迎。随着磁浮交通的快速发展，磁浮线路的不断扩展，地震发生时桥上行驶列车的可能性越来越高，地震作用对轨道-桥梁结构和磁浮列车安全性都构成了严重威胁。近年来，众多学者针对磁浮车轨耦合振动开展了大量研究，但关于磁浮交通系统地震响应的研究较少。ZHANG 等[1-2]建立了高速磁浮车桥系统耦合振动分析模型，对系统的动力响应进行了数值模拟。李小珍等[3-5]考虑PID 主动悬浮控制建立了中低速磁浮车桥系统耦合振动数值模型，研究了中低速磁浮系统的动力相互作用特性。LI 等[6-8]基于现场动载试验，对中低速磁浮车辆和桥梁系统的动力相互作用机理进行了分析。对于车桥系统的地震响应，众多学者对轮轨交通系统的地震响应特征进行了研究。XIA等[9]采用相对运动法研究了非一致地震激励对车辆和桥梁动力响应的影响。雷虎军等[10-11]分别采用相对运动法和直接求解法计算了车桥系统的地震响应，分析了地震输入方法对系统响应的影响。ZHANG 等[12]基于虚拟激励法和精细积分技术研究了横向水平地震作用下车桥系统的非平稳随机动力响应。不同于轮轨交通，磁浮系统利用非接触的电磁力实现列车的悬浮和导向，在求解地震响应时，需要考虑悬浮系统的主动控制，黄凤华等[13-14]分别采用相对运动法和直接求解法建立了中低速磁浮列车-桥梁系统地震响应分析模型，分析了拟静力分量对地震响应特性的影响，计算了时速60～120 km 车辆和桥梁的地震响应，但是没有考虑轨排结构，而轨排结构对磁轨相互作用有重要的影响，不可忽视。为了探讨中速磁浮(设计时速160～250 km)列车-轨道-桥梁系统的地震响应特性，分析地震作用对系统耦合振动的影响，本文基于PID主动悬浮控制，采用直接求解法，在绝对坐标系下建立了考虑轨排结构的中速磁浮列车-轨道-桥梁系统地震响应分析数值模型，计算了只考虑车辆作用、只考虑地震作用以及同时考虑车辆和地震作用3种工况下系统的动力响应，并通过参数分析研究了车速对系统地震响应的影响。

1 数值计算模型

1.1 磁浮车辆模型

磁浮车辆主要由车体、悬浮架、二系悬挂和电磁铁等组成，每节车体通过二系悬挂与5对悬浮架连接，每对悬浮架包括左右2套悬浮架，由防侧滚梁连接，使得两侧悬浮架运动解耦，电磁铁固定在悬浮架的底部。车体和悬浮架视为刚体，不考虑其纵向运动。车体考虑沉浮、横移、点头、摇头和侧滚5个自由度，分别用yc，zc，αc，βc和γc表示；悬浮架考虑到防侧滚梁的作用仅考虑沉浮、横移、点头和摇头4 个自由度，分别用yb，zb，αb和βb表示。单节车辆共计45 个自由度，车辆模型如图1所示。

作用在车体和悬浮架上的荷载分布如图2 所示，图中：Fbjyi(j=1～5,i=1～4)和Fbjzi(j=1～5,i=1～4)分别表示第j个悬浮架第i个竖向和横向悬挂力；fmjzi(j=1～5,i=1～8)和f'mjyi(j=1～5,i=1～8)分别表示第j个悬浮架第i个电磁铁的导向力和平衡车辆重力后的调整悬浮力。根据D’Alembert 原理，建立车辆系统运动方程：

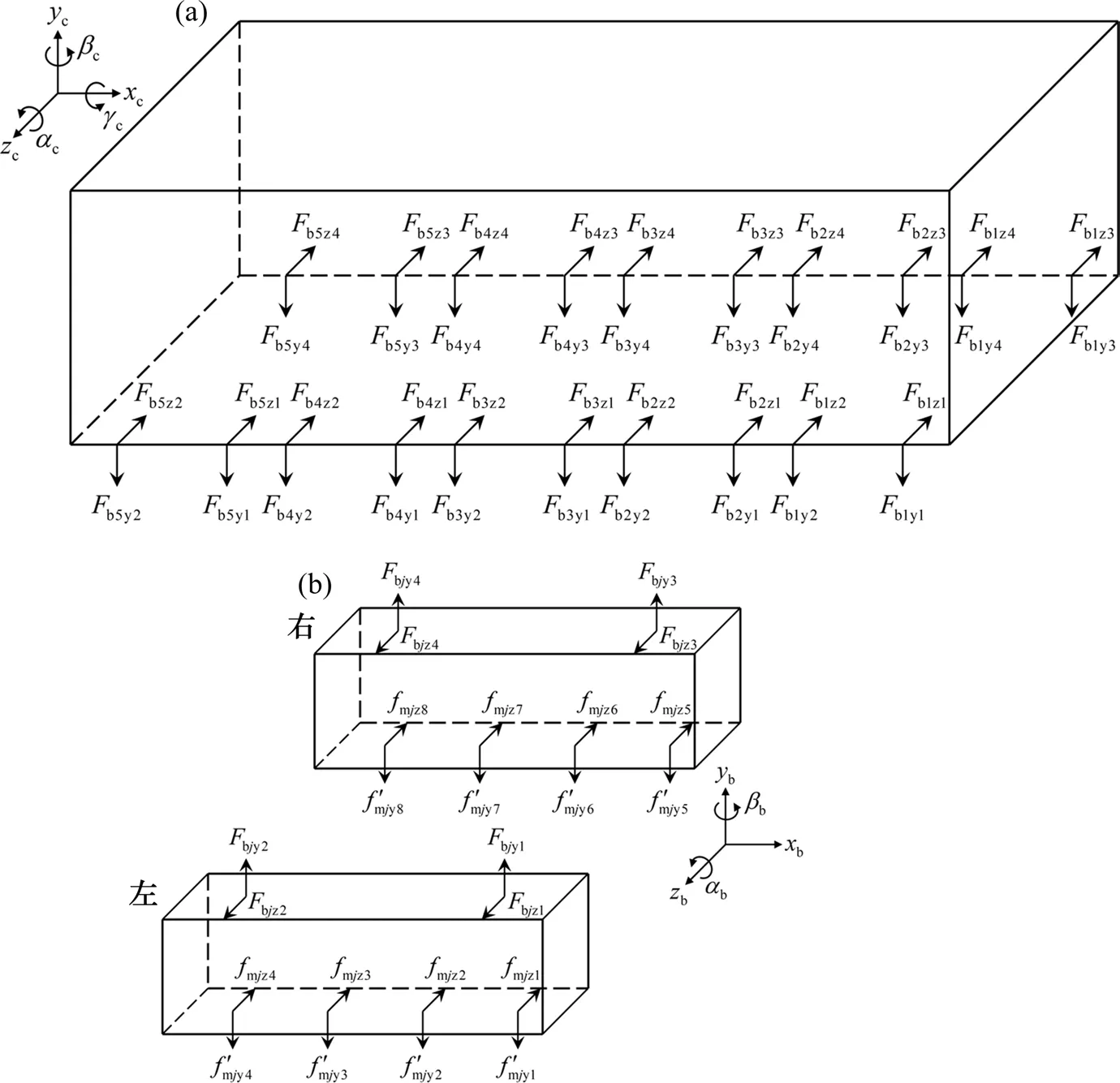
图2 车辆受力示意图Fig.2 Force diagram of vehicle

式中：Mv，Cv和Kv分别为车辆系统运动方程的质量、阻尼和刚度矩阵；，和Xv分别为车辆系统的加速度、速度和位移列向量；Fv为作用于车辆系统的悬浮力和导向力列向量。

1.2 轨道-桥梁模型

基于有限元法建立简支轨道-桥梁模型，如图3 所示。采用空间梁单元模拟F 轨、桥梁和桥墩，弹簧单元模拟轨枕扣件和支座，地震波施加于桥墩底部。将轨道-桥梁结构自由度分别按支撑节点和非支撑节点分块，则在绝对坐标系下，结构的运动方程为

图3 轨道-桥梁模型Fig.3 Model of track-bridge structure

式中：M，C和K分别为质量、阻尼、刚度矩阵；u，和分别为绝对位移、速度、加速度列向量；下标ss 和gg 分别为非支撑节点和支撑节点自由度项，下标sg 和gs 分别为非支撑节点和支撑节点之间的耦合自由度项；Fvr为车辆作用在轨道上的悬浮电磁力列向量，Fgg为支撑反力项。

将式(2)第1 行展开，并消去支撑反力项Fgg，得到

采用模态叠加法对运动方程解耦：

式中：ϕn为第n阶模态；qn为第n阶模态对应的广义坐标。

将式(4)代入式(3)，得到轨道-桥梁系结构的运动方程：

式中：α和β为Rayleigh 阻尼系数；ωn为第n阶圆频率；ζn为第n阶模态阻尼比。

采用直接求解法对上述运动方程求解，需要同时输入地震波的位移、速度和加速度时程。

1.3 控制系统模型

磁浮车辆利用电磁铁和F轨之间的电磁力实现悬浮和导向，电磁力包括悬浮力fmy和导向力fmz，计算表达式为[15]

式中：μ0为空气磁导率；Am为磁极面积；h为悬浮间隙；c为导向间隙；Wm为磁极宽度；Nconst为恒定电流线圈数；Iconst为恒定电流；Nc为控制电流线圈数；ic为控制电流。

悬浮系统本身是开环不稳定系统[16]，必须引入悬浮控制器进行反馈控制以达到悬浮间隙在容许范围内波动的要求，实现车辆的稳定悬浮。基于比例-积分-微分(PID)控制器，进行反馈调节并输出控制电压，其数学表达式如下：

式中：KP，KI和KD分别为比例、积分和微分参数；k为控制时间；uc为控制电压；Δh为悬浮间隙波动量；为悬浮间隙变化率。

1.4 数值求解流程

基于本文建立的车辆、轨道-桥梁和悬浮控制系统及其相互作用关系，采用Fortran 语言编制了相应的分析程序。其中，车辆系统的运动方程(1)和轨道-桥梁的运动方程(5)通过Runge-Kutta 法求解，车辆-轨道-桥梁系统在当前时刻的动力响应是通过在每个增量时间步进行迭代确定的，在迭代过程中，当前时刻的磁浮间隙状态由上一时刻车辆和轨道的振动状态确定。详细计算流程如图4所示。

图4 数值计算流程Fig.4 Flowchart of numerical calculation program

2 程序验证

2.1 计算参数

车辆选用长沙3节编组中低速磁浮列车，具体参数参照文献[3]中磁浮车辆的参数，额定悬浮间隙设定为10 mm。轨道-桥梁结构参考现有磁浮轨道梁桥工程实例和中低速磁浮规范拟定，主要计算参数见表1。由于尚无成熟的磁浮线路不平顺谱，采用文献[17]推荐的轨道不平顺谱。

表1 轨道-桥梁主要计算参数Table 1 Calculation parameters of track-bridge structure

以典型记录EI Centro 地震波作为输入激励。由于地震响应分析需要同时输入地震波加速度、速度和位移时程，而目前的地震记录仪主要记录的是地震加速度信号，因此先进行高通滤波以消除原始地震加速度信号中的漂移误差，然后对修正后的加速度时程进行频域积分以得到地震波速度和位移时程。处理后的地震波时程如图5 所示，横向和竖向地震峰值地面加速度分别设为0.10g和0.065g。对于地震作用下的列车-轨道-桥梁系统，地震的开始时刻是不确定的，计算时假定车辆在入桥前0.75 s 时地震荷载开始施加，此时当车辆以200 km/h行驶时，达到地震动峰值时刻在求解跨桥梁满载时间区间内。

图5 地震波时程曲线Fig.5 Time-history curve of seismic wave

2.2 模型验证

为验证所建立模型的正确性和程序计算的可靠性，分别从车轨耦合振动响应和地震响应2个方面对计算结果进行验证：1) 只考虑车辆作用，将程序计算得到的桥梁跨中位移与文献[3]中80 km/h速度下的现场实测结果进行对比；2) 同时考虑车辆和地震作用，将桥梁跨中位移和车体加速度与HUANG 等[14]针对中低速磁浮80 km/h 速度下车桥地震响应的仿真计算结果进行对比。从图6(a)可以看出，在车辆荷载作用下，程序计算结果与实测值较为吻合，桥梁位移幅值接近，但位移波形有所差异，这是由于仿真计算中的轨道不平顺与现场难以保持一致，且仿真计算时外界干扰因素较少。在车辆和地震共同作用下，程序计算的桥梁和车体动力响应与文献[14]计算值在波形上基本重合，之间的微小差异是因为本文考虑了轨道结构的影响。

图6 程序仿真结果验证Fig.6 Validation of program simulated results

3 动力响应

为了研究地震作用对磁浮列车-轨道-桥梁系统动力响应的影响，分别考虑如下3种工况：车辆荷载和地震荷载同时作用、仅考虑车辆荷载以及仅考虑地震荷载，计算列车-轨道-桥梁系统的动力响应，前2种工况下车辆速度为200 km/h。

3.1 车辆动力响应分析

图7 和图8 给出了磁浮间隙和车体加速度时程曲线，可以看出，地震作用放大了电磁铁的磁浮间隙和车体加速度响应，尤其是横向上分别放大近9倍和18倍。竖向由于PID主动控制的作用，放大效果相对不明显。3 种工况下系统的响应幅值对比如表2所示。

表2 3种工况下列车-轨道-桥梁系统响应幅值比较Table 2 Comparisons of maximum responses of vehicle-track-bridge system under three conditions

图7 磁浮间隙时程曲线Fig.7 Time-history curves of magnetic gap

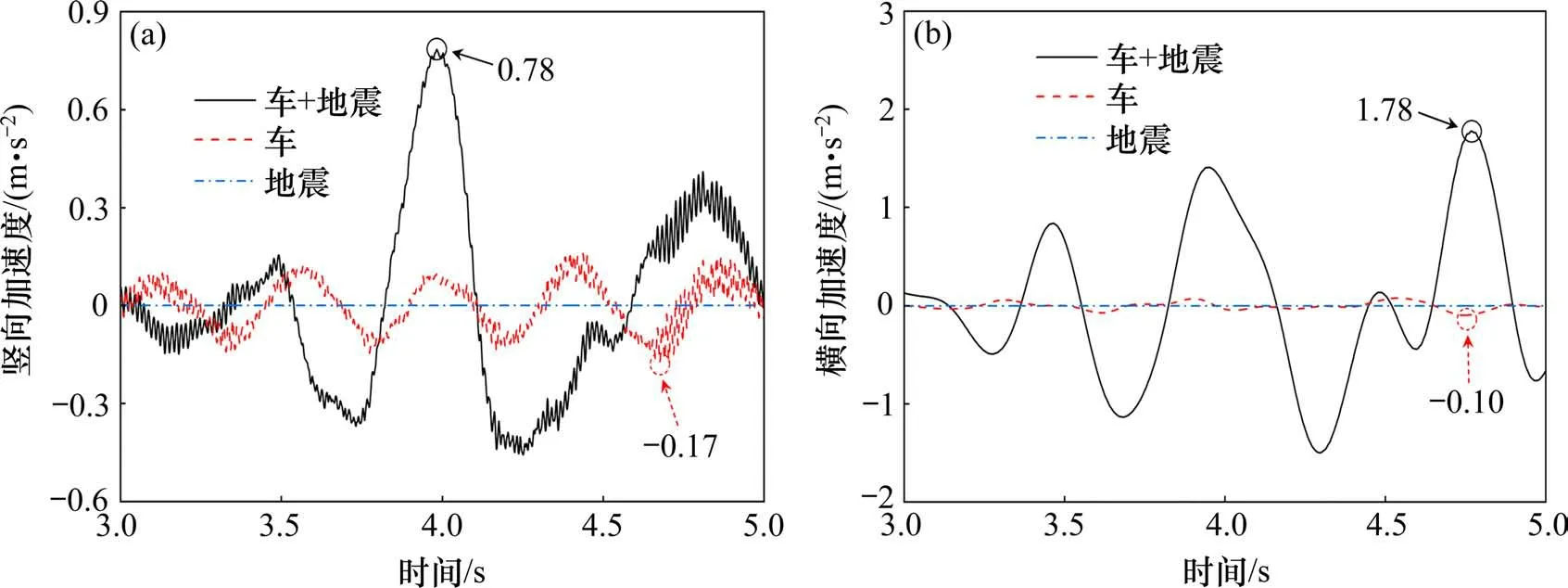
图8 车体加速度时程曲线Fig.8 Time-history curves of vehicle acceleration

3.2 轨道-桥梁动力响应分析

对于轨道-桥梁结构，在车辆和地震共同作用下，跨中竖向位移远大于仅考虑地震作用时，在仅考虑车辆作用下的位移曲线周围波动，如图9(a)和9(c)所示，说明车辆荷载是影响轨道-桥梁竖向位移的主要因素，但忽略地震作用仍会低估竖向位移近19%。而对于横向响应，在车辆和地震共同作用下的跨中横向位移远大于仅考虑车辆作用时，时程曲线波形与仅考虑地震作用时相近，如图9(b)和9(d)所示，说明地震是影响轨道-桥梁横向位移的主要激励。尽管如此，横向位移在车辆和地震共同作用下的幅值也是仅考虑地震作用时近1.5 倍，位移响应幅值如表2 所示。因此，对于地震作用下的列车-轨道-桥梁耦合系统，忽略车辆或地震作用都会低估轨道-桥梁的位移响应。

图9 轨道-桥梁跨中位移时程曲线Fig.9 Displacement time-history curves at mid-span of track-bridge structure

图10进一步给出了轨道-桥梁结构的加速度频谱图。图中，f1，f2和f3是由车辆行驶产生的特征频率，通过fi=v/Li计算[18]，fi为车辆的特征频率(Hz)，v为车辆行驶速度(m/s)，Li为车辆的特征长度(车体长度L1=15.75 m，悬浮架长度L2=3.15 m及电磁铁长度L3=0.78 m)。从图中可以看出，轨道-桥梁的振动主要由固有频率、车辆特征频率(f1=3.53 Hz，f2=17.64 Hz，f3=70.55 Hz)及其倍频组成。当同时考虑车辆和地震作用时，轨道-桥梁竖向振动响应在低频区域(0～10 Hz，主要为1 阶固有频率)远大于仅考虑车辆作用时，与仅考虑地震作用时相近，在高频区域(50～150 Hz，主要由车辆的特征频率控制)与仅考虑车辆作用时接近；对于横向振动，主要以横向1 阶固有频率振动为主，在低频区域同时考虑车辆和地震作用时的振动响应同样远大于仅考虑车辆作用时的响应，与仅考虑地震作用时相近。频域响应分析表明，地震作用会显著放大轨道-桥梁结构的1 阶固有频率振动响应，考虑是因为地震波频率主要集中在低频部分，与结构的1阶固有频率接近。

图10 轨道-桥梁跨中加速度频谱Fig.10 Acceleration spectrum at mid-span of track-bridge structure

3.3 不同速度下动力响应

为进一步揭示地震作用的影响，图11 和图12给出了车体加速度幅值和桥梁跨中位移幅值随车速的变化规律。可以看出，同时考虑车辆和地震作用时车体加速度幅值在车速160～250 km/h 均远大于仅考虑车辆作用时，尤其是横向加速度幅值。另一方面，从图中还可以发现，同时考虑车辆和地震作用时的车体加速度幅值随车速提高并非单调变化，且与仅考虑车辆作用时的变化规律无明显相关性。这是因为地震动开始时刻是一致的，但在不同车速下，车辆在轨道上的位置是不一致的，所以很难确定车体加速度响应在地震作用下的叠加效果是增强还是减弱。考虑到车辆速度的复杂影响，建议在计算车体地震响应时，将地震动达到峰值的时刻与仅有车辆作用下的车体响应峰值时刻设为一致，以分析最不利条件下车体地震响应特性。

图11 车体加速度幅值随车速的变化Fig.11 Variation of vehicle acceleration amplitude with vehicle speed

图12 桥梁跨中位移幅值随车速的变化Fig.12 Variation of displacement amplitude at mid-span of bridge with vehicle speed

对于桥梁结构，同时考虑车辆和地震作用时的跨中位移随车速变化规律与仅考虑车辆作用时没有明显相关性，这与车体加速度响应相似。此外，还发现跨中竖向位移随车速提高非单调变化，而横向位移随车速提高呈现明显的下降趋势。这是因为桥梁竖向受到车辆荷载的影响较大，而车辆和地震2 种荷载的叠加效果增强与否是不确定的，横向主要受地震荷载影响，随着车速提高，车辆通过桥梁所需时间减少，地震荷载的作用时间也会随之减少，桥梁满载的时间区间可能会错过地震动峰值运动。

4 结论

1) 地震作用对磁浮车辆-轨道-桥梁系统振动响应影响明显，对系统横向振动的影响远大于对竖向振动的影响。

2) 针对文中的计算条件，轨道-桥梁结构跨中竖向位移受车辆作用影响较大，同时考虑车辆和地震作用下的跨中竖向位移时程曲线在仅考虑车辆作用下的位移曲线周围波动，而跨中横向位移主要受地震作用影响。

3) 轨道-桥梁结构的频域响应与车辆荷载的特征频率及结构固有频率密切相关，考虑地震作用后，轨道-桥梁结构的1 阶固有频率振动响应会被显著放大。

4) 当车辆以160～250 km/h 运行时，同时考虑车辆和地震作用下的车体加速度幅值和桥梁跨中位移幅值随车速的变化规律与仅考虑车辆作用时没有明显相关性，随着车速提高，车体加速度幅值与桥梁跨中竖向位移幅值并非单调变化，而桥梁跨中横向位移幅值呈现下降趋势。