桥跨布置对连续梁桥上轨道地震响应影响规律研究

谢浩然 ，徐凌雁，许婧，闫斌

(1.中国铁路设计集团有限公司，天津 300308；2.中南大学 土木工程学院，湖南 长沙 410075；3.中国铁路投资集团有限公司，北京 100097)

桥上无缝线路其钢轨除受温度力作用外，还受纵向附加力的影响[1-2]。国内外学者针对铁路梁轨相互作用已进行广泛细致的研究[3-5]，考虑轨道结构后，桥梁墩台结构其纵向受力有较大增加，在进行墩台检算、优化设计时须考虑轨道结构的影响[6-7]。相比传统代数求和各纵向力的方法，考虑线路纵向阻力进行加载历史迭代后，结构受力明显降低，更贴近实际[8]。既有研究中针对进行梁轨系统地震响应分析多没有考虑轨道结构，或将线路纵向阻力按照线性方式简化处理。对于下部桥跨结构未考虑桥墩结构桩土相互作用，支座滑动摩阻力予以忽略。另外，大跨度连续梁桥往往通过设置钢轨伸缩调节器(以下简称“调节器”)来降低钢轨结构受力，但调节器结构破坏了无缝线路连续性，显著改变了桥上轨道和桥梁下部结构的受力情况，同时也降低了线路平顺性[9-10]，成为无缝线路中的薄弱环节，地震碰撞下受力机理十分复杂。鉴于桥梁结构体系特殊性、活载工况繁多，地震作用下梁轨相互作用研究仍相对不足，桥跨结构布置方式对系统地震响应的影响规律仍不明确。本文基于桥梁与轨道相互作用原理，采用经验证的桥上地震碰撞分析大质量法，以新建昌景黄铁路大跨度连续梁桥为研究对象，建立了考虑结构非线性约束的桥梁与轨道相互作用有限元模型。分析地震碰撞作用下连续梁桥上无缝线路受力，研究桥跨结构布置关键参数对梁轨系统地震相互作用影响规律。

1 地震和碰撞效应计算模型

1.1 梁轨相互作用计算参数

扣件系统包括小阻力扣件和常阻力扣件，主要分为有砟轨道用常阻力弹条II 型和无砟轨道用WJ-7 和WJ-8 型，扣件竖向动刚度取静刚度1.5 倍，为6×107N/m。参考铁科院、铁四院以及铁二院实测数据，现行《铁路无缝线路设计规范》中将小阻力扣件的弹塑性临界点设为0.5～1 mm，取0.5 mm[11]。线路纵向阻力表达式[9,12]为：

式中：r1为无砟轨道常阻力扣件线路纵向阻力；r2为无砟轨道小阻力扣件线路纵向阻力；r3为有砟轨道道床纵向阻力；x1为钢轨-承轨台纵向相对位移。

有砟轨道等效道床横向阻力取11.5 kN/m，通过试验拟合，无砟轨道横向阻力表达式为：

式中：x2为钢轨-承轨台横向相对位移。

计算参数中除考虑滑动支座摩阻力外，还在梁体上翼缘处增加二期恒载质量模拟梁轨质量分布，对于双线无砟轨道，取为130 kN/m。在进行桥墩截面弯矩-曲率分析时，桥墩采用6 个自由度的三维非线性梁单元模拟，如图1所示。

在进行无缝线路梁轨分析时，除墩底外，路基段同样建立大质量单元，施加与相邻桥台相同的地震激励，碰撞间隙取梁缝100 mm。

参照《铁路工程抗震设计规范》[13]，生成El Centro人工波作为地震激励，场地类型为Ⅳ类，对应场地特征周期0.75 s。

1.2 有限元模型

有限元分析中，采用梁单元模拟钢轨、梁体与桥墩，用竖向刚臂模拟梁高，用非线性杆单元模拟线路纵向阻力，扣件竖向刚度由线性弹簧模拟。用非线性碰撞单元模拟随机碰撞作用。采用线性弹簧和阻尼器并联的Kelvin 非线性碰撞单元，模拟地震中梁体的碰撞效应。通过墩底转动弹簧模拟群桩-土体共同作用。桥墩底部采用非线性梁单元，模拟桥墩的弯矩-曲率曲线，以便考虑地震中可能出现的塑性铰。系统采用瑞利阻尼，阻尼系数α和β采用下式[14]：

式中：w1和w2为对结构竖向振型贡献最大的前2阶频率，阻尼比h取0.05。

建立的有限元模型如图2所示。

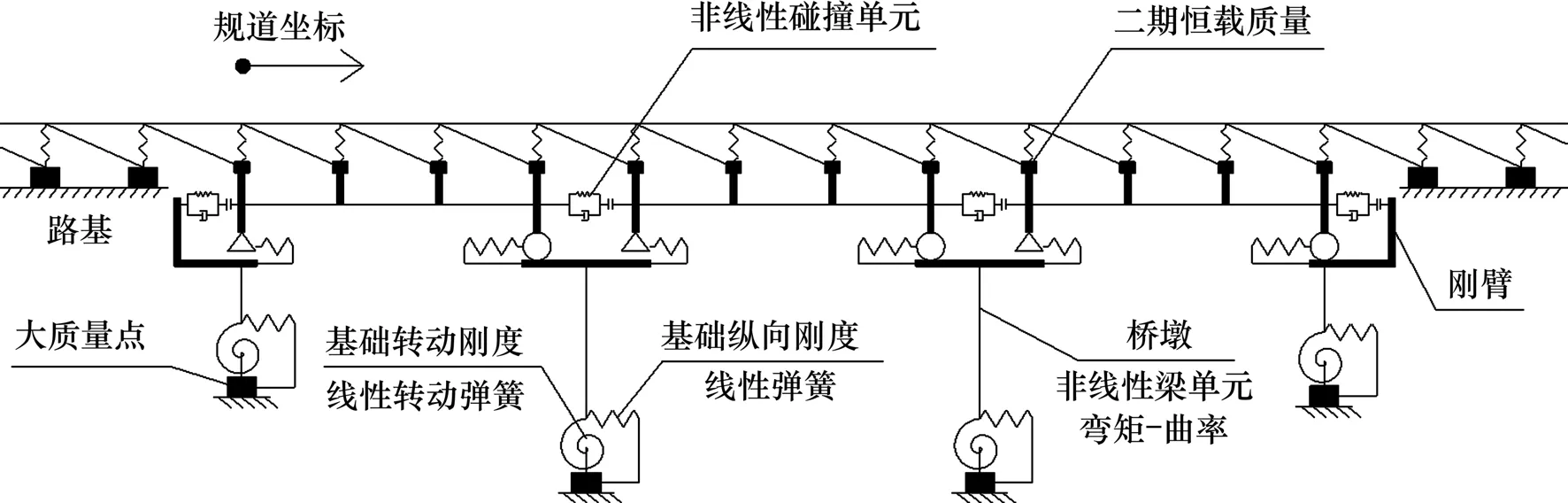
图2 梁轨相互作用地震碰撞有限元计算模型Fig.2 FEM for seismic collision of beam-bridge interaction

2 地震和碰撞效应验证

采用CHN60 轨，以3 跨32 m 简支T 梁铺设有砟轨道作为算例，左端为固定支座，右端滑动支座不考虑滑动支座摩阻力。道床纵向阻力取10 kN/m，梁体截面面积3.327 6 m2，惯性矩1.96 63 m4，C40混凝土弹性模量取33 GPa，计算8 度设计地震El Centro波作用下结构受力，不考虑行波效应，与文献[15]对比见表1。

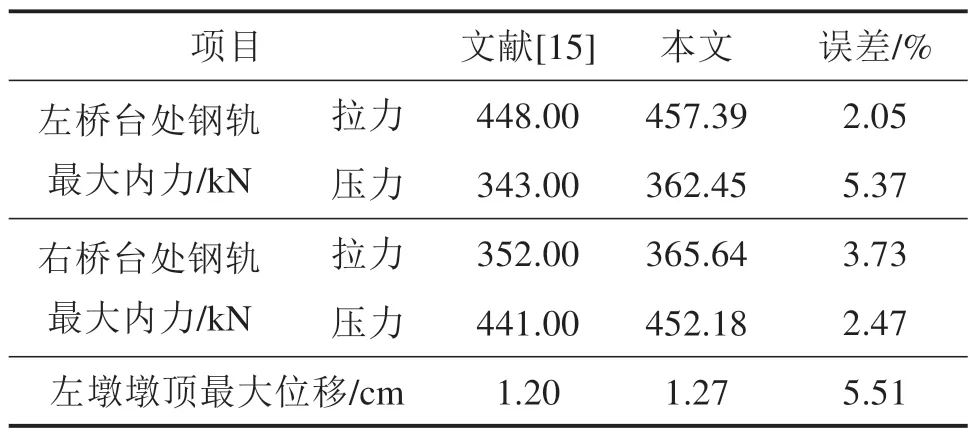
表1 模型验证数据对比Table 1 Model verification and data comparison

在表1中可以看到，由于文献对比算例中部分参数难以获取，地震波参数与阻尼系数不同，本文计算结果与文献有相对差异性但基本规律较为吻合，可认为该梁轨系统地震有限元模型与计算理论可用。

3 轨道结构布置

为消除边界效应影响，在简支梁两端各建立100 m 路基上的钢轨，研究线路纵向阻力以及钢轨伸缩调节器等轨道结构关键设计参数对地震一致激励作用下梁轨互制的影响。取(60+100+60) m 连续梁两侧各相接8 跨标准32 m 简支梁，加速度峰值取设计地震0.3g[16-17]。连续梁左侧支座为坐标原点，Z和Y分别表示连续梁左、右侧简支梁，连续梁墩台编号依次为为L1～Ln，梁缝同理用SZ 和SY表示，如图3。

图3 连续梁和简支梁桥跨布置示意图Fig.3 Layout of CWR on continuous bridge and simply supported bridge

3.1 线路纵向阻力

不考虑钢轨伸缩调节器作用，分析采用小阻力扣件(连续梁范围、连续梁边跨及相邻一孔跨简支梁)、有砟轨道道床阻力和无砟轨道扣件阻力4种纵向阻力模型对梁轨系统地震响应的影响，钢轨应力和桥梁墩台受力如图4和图5所示。

图4 线路纵向阻力对梁轨系统地震位移影响Fig.4 Influence of the longitudinal resistance on seismic displacement

图5 线路纵向阻力对连续梁地震受力影响Fig.5 Influence of the longitudinal resistance on seismic force

由图4 可以看到，随着线路纵向阻力的提高，钢轨结构承受更多下部桥梁结构传递而来的纵向力，增强了对桥梁约束，墩顶位移、梁轨相对位移以及梁端位移均大幅减小。墩顶最大位移发生在连续梁制动墩，并由相邻简支梁制动墩向两侧分散减小，最大位移为铺设有砟轨道工况，达0.4 m。梁轨相对位移、梁端位移最大值均发生在连续梁梁端活动支座处，最大分别为0.21 m 和0.23 m，均为采用有砟轨道阻力方案。相对于在连续梁边跨及相邻一孔跨简支梁上铺设小阻力扣件方案，仅在连续梁范围内铺设小阻力扣件的方案其墩顶位移、梁轨相对位移及梁端位移均较小，降幅最大为16.7%，相对来说更优。

在图5中，采用无砟轨道阻力方案结构位移较小，但钢轨受力较大，最大为297 MPa，连续梁范围内铺设小阻力扣件方案钢轨受力最小，为208 MPa，降幅29.9%。最大墩底剪力同样发生于连续梁L2 制动墩，在图5(c)时程曲线中可以看到4 260 kN，为采用有砟轨道阻力方案。综上比较，大跨度连续梁上设计钢轨强度检算困难时需采用小阻力扣件方案，地震影响下建议采用仅连续梁范围铺设小阻力扣件，使结构受力及位移均保持在较小限度内。

3.2 钢轨伸缩调节器

温度跨度较大，升温荷载作用下当采用铺设小阻力扣件方案仍不满足钢轨无缝线路强度检算时，大跨度连续梁上往往采用梁端设置调节器来大幅减小钢轨应力。梁体升温30 ℃[11,18]，钢轨升温40 ℃[19]，通过设置如下4种方案，分别为：连续梁范围铺设小阻力扣件、连续梁中央设置调节器、连续梁活动端设置调节器、连续梁活动端设置调节器而对侧边跨及相邻一孔跨简支梁铺设小阻力扣件，研究地震作用下伸缩调节器的影响，如图6所示。

图6 连续梁桥上钢轨伸缩调节器布置方案Fig.6 Arrangement scheme of rail expansion adjuster on continuous bridge

不同钢轨伸缩调节器布置方案下梁轨系统受力如图7所示。

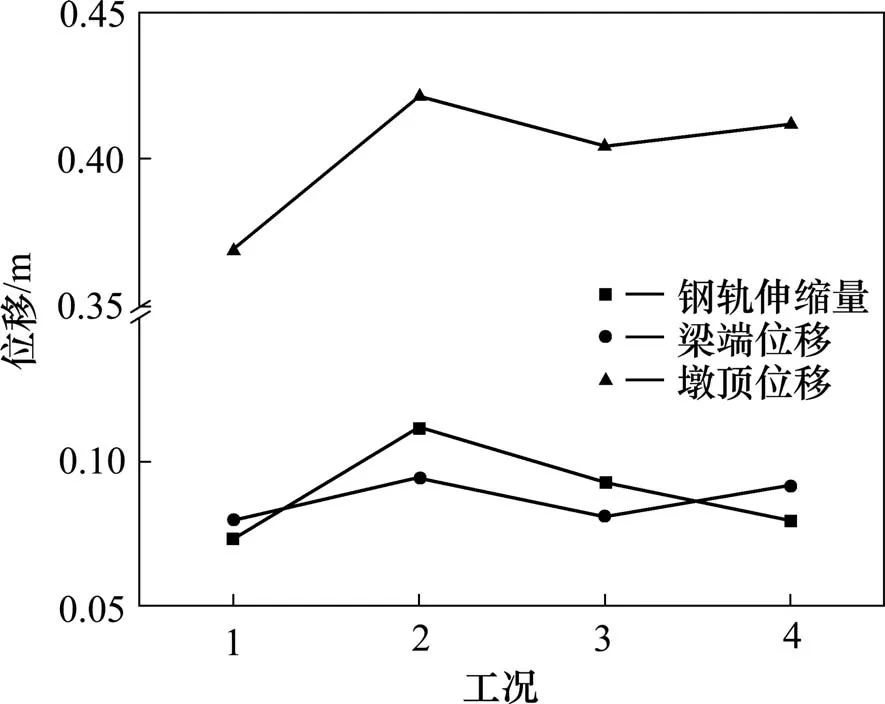
图7 钢轨伸缩调节器对梁轨系统地震位移影响Fig.7 Influence of the rail expansion adjuster on seismic displacement

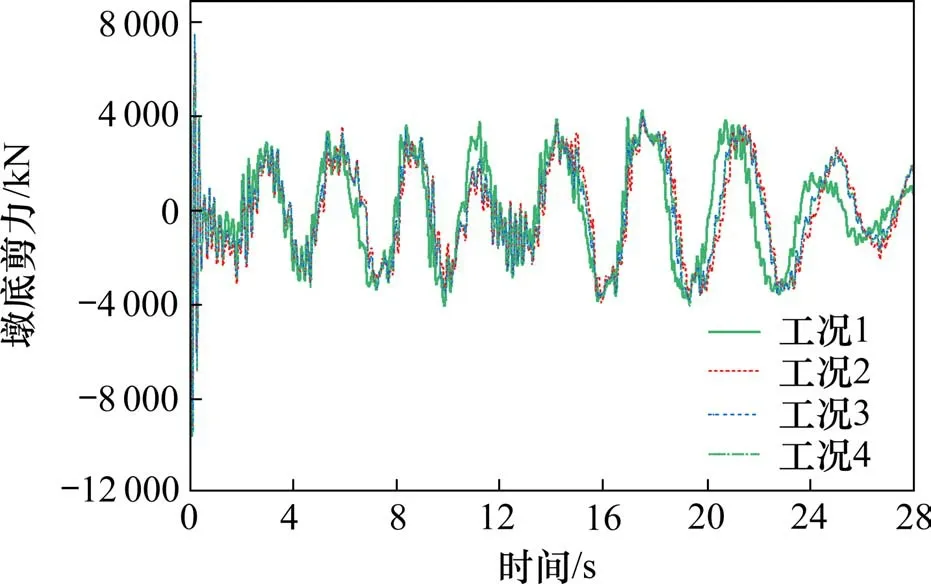
图8 钢轨伸缩调节器对制动墩地震受力影响Fig.8 Influence of the rail expansion adjuster on seismic force

地震作用，不同调节器设置工况钢轨应力最大为211 MPa，其中连续梁活动端设置调节器方案钢轨应力为176 MPa，降幅16.6%，结构受力上方案较优。工况2在连续梁中央设置调节器其钢轨伸缩量、梁端位移及墩顶位移均最大，其中墩顶位移达0.422 m，较工况1 仅铺设小阻力扣件增幅14.4%，考虑结构动位移应避免调节器设置在桥梁中央，也不利于梁轨变形协调。

相较于仅设置小阻力扣件，铺设调节器后墩台受力较大，时程分析中地震初始最大墩底剪力为7 467 kN，连续梁制动墩承受巨大水平力，稳定后最大剪力稳定为4 268 kN。地震作用下设置调节器对梁轨系统位移及制动墩受力并无明显改善作用。考虑无缝线路钢轨强度检算要求，当确需设置调节器时，建议仅在连续梁活动端设置(工况3)，必要时可在对侧边跨及相邻一孔跨简支梁同时铺设小阻力扣件(工况4)。

4 桥梁结构布置

温度力与附加力作用下梁轨互制作用，钢轨位移受一孔跨桥梁两端线路纵向阻力约束[20]。升温作用下固定支座端以外线路纵向阻力阻止钢轨向活动端向伸缩，固定端处钢轨受拉。活动支座端以外线路纵向阻力抵抗钢轨向固定端向伸缩，活动端处钢轨受压。研究连续梁与简支梁孔跨布置以及关键结构参数等敏感因素对分析地震力作用下梁轨系统受力具有重要意义。

4.1 简支梁跨数

探讨地震作用下连续梁两侧多跨简支梁简化计算方法，以(60+100+60) m 跨度连续梁桥为例，孔跨及支座布置方式同图3 所示，分别建立2～10跨简支梁，计算结果见图9。

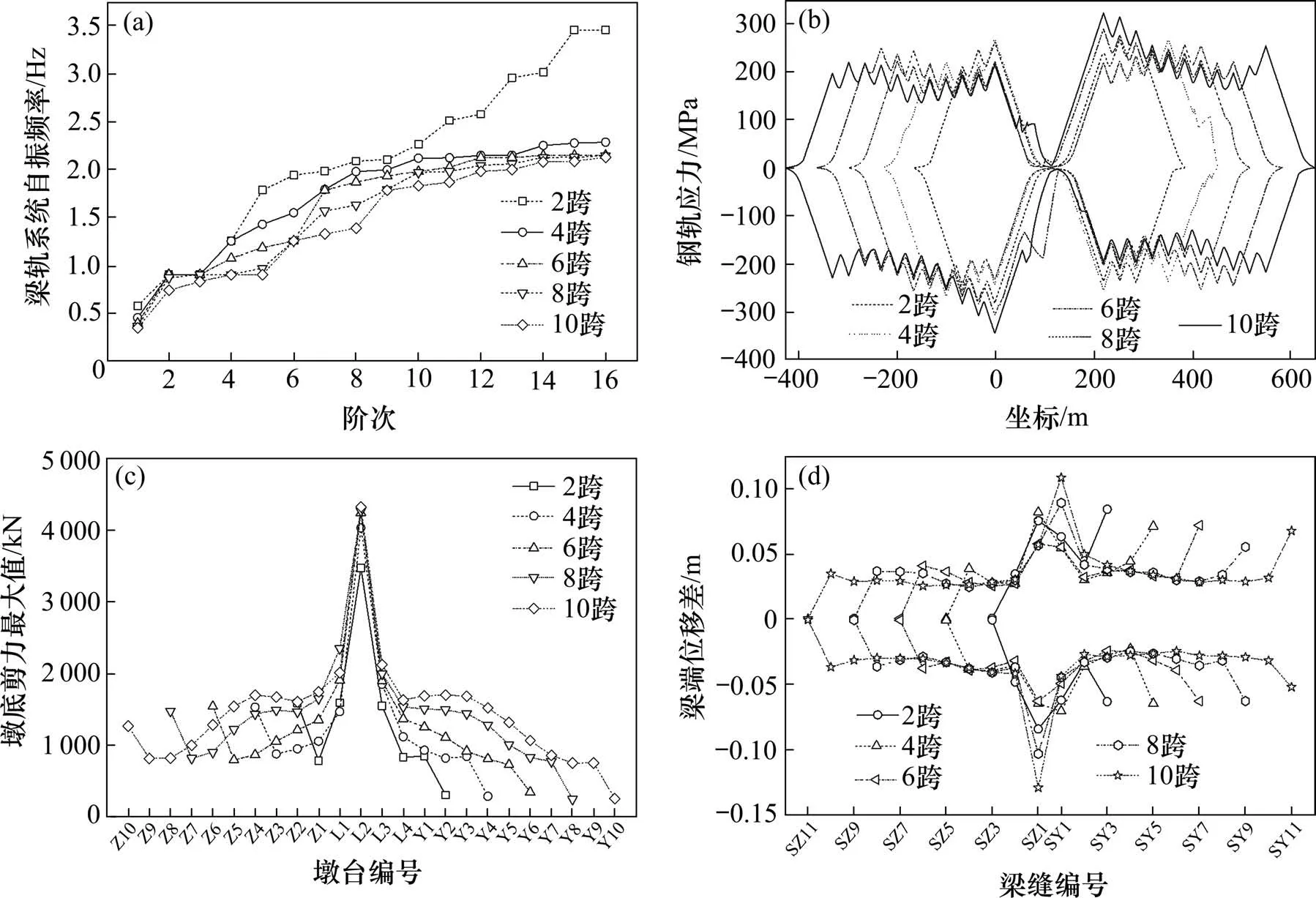
图9 简支梁跨数对梁轨系统地震响应影响Fig.9 Influence of simply supported bridge spans force on seismic response

地震作用下连续梁两侧相邻简支梁跨数对梁轨系统超过9阶的高阶自振频率影响较大，当简支梁跨度超过6 跨后各阶自振频率趋向稳定。图9(b)中，连续梁两端钢轨最大拉、压应力(SZ1 和SY1处)随简支梁跨数的增加呈先减后增趋势，当跨数为6～8 跨时受力最小。桥梁墩台剪力受跨数影响较小，跨数超过6跨后，连续梁制动墩受力趋于稳定，其中当6～8 跨时，制动墩最大剪力为4 237～4 260 kN，增幅减少为0.5%，并且两侧简支梁各墩受力逐渐减小。

在图9(d)中，随着跨数增加，梁端位移差不断增加，最大位移同样发生于与简支梁相接梁缝处，在靠近连续梁L2 制动墩的SZ1 梁缝处，梁体间梁缝扩大的反向位移明显，此时易发生落梁现象；同样，在远离连续梁制动墩的SY1 梁缝处，梁体间梁缝缩小的对向位移明显，此时易发生碰撞现象。8 跨简支梁时接近碰撞线0.1 m，建议按照连续梁两侧接8跨简支梁进行地震作用简化计算。

4.2 连续梁跨度

以主跨60～100 m 大跨连续梁为例，各跨度桥梁布置方案见表2。

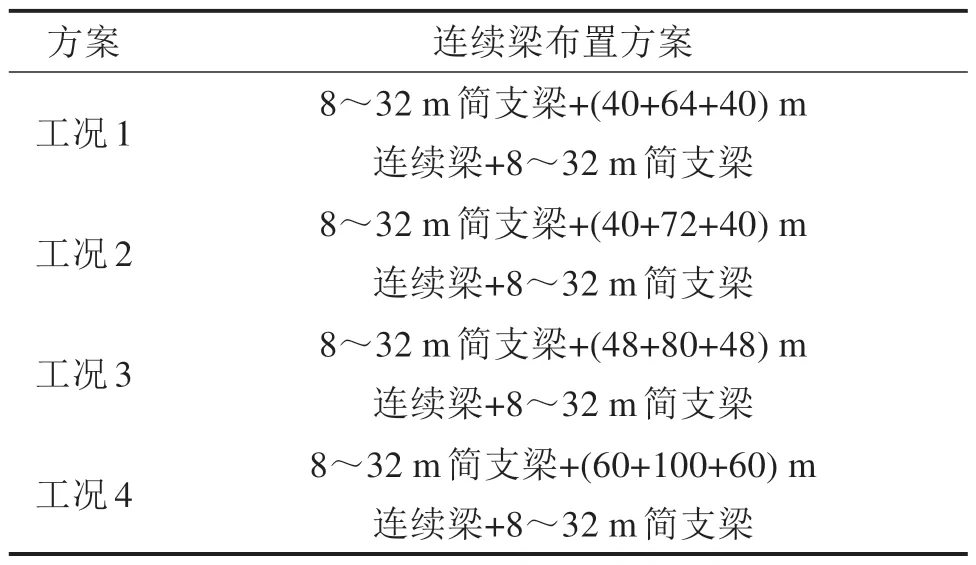
表2 连续梁跨度布置方案Table 2 Continuous bridge span layout scheme

分析一致激励下梁轨系统的地震响应，桥梁和墩台见图10以及表3。

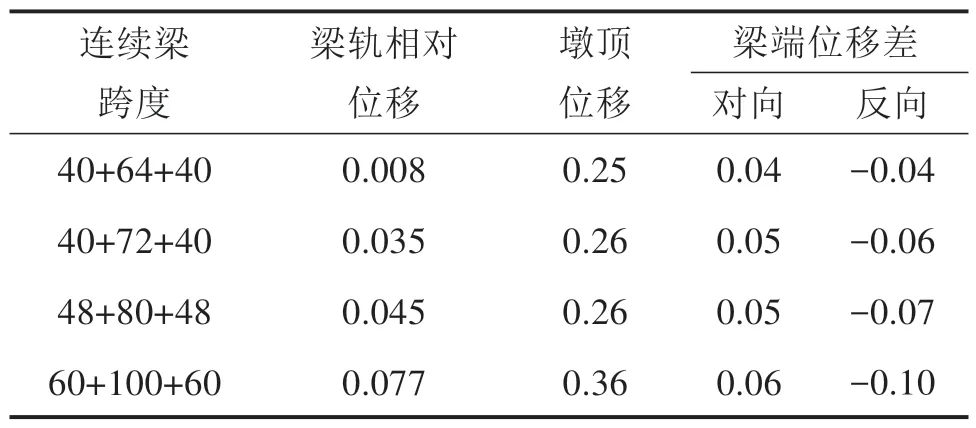
表3 连续梁跨度下梁轨系统地震最大位移Table 3 Maximum seismic displacement under continuous bridge span m

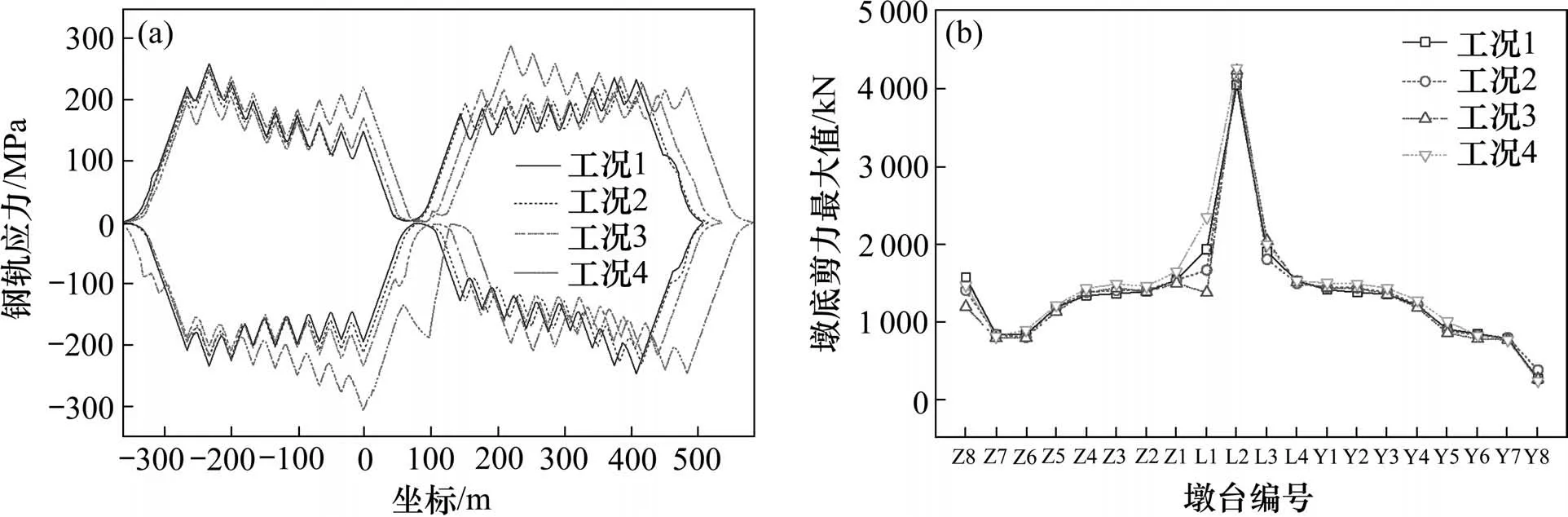
图10 连续梁跨度对梁轨系统地震响应影响Fig.10 Influence of continuous bridge span on seismic response

在图10 中可见，随着连续梁跨度的增大，线路累计纵向阻力不断增加，钢轨应力不断增大，主要出现在连续梁与简支梁相邻梁缝附近。墩台剪力增加平缓，影响较小。

在表3中可以看到，与结构受力趋势一致，地震作用下结构各项位移指标随连续梁跨度增大同样增加(梁端位移差中“对向”指梁端作相对靠近运动，“反向”指梁端作相对远离运动)。跨度超过(60+100+60) m 后，钢轨应力大幅度增加，并且梁端反向位移差超过0.1 m，落梁现象几率增加。

4.3 支座非顺序布置

假定线路大里程向纵坡为正(上坡)，此时为减小自重位移影响，设计简支梁固定端设置在小里程向[21-22]。若桥梁温度跨度过大导致钢轨受力大于屈服强度，则需要调整连续梁两端简支梁固定支座布置方式，尽可能减小温跨，满足钢轨强度要求。

梁体升温30 ℃，以(60+100+60) m 连续梁为例，分析一致激励下梁轨系统的地震响应，连续梁两侧8跨简支梁支座布置方案见图11。

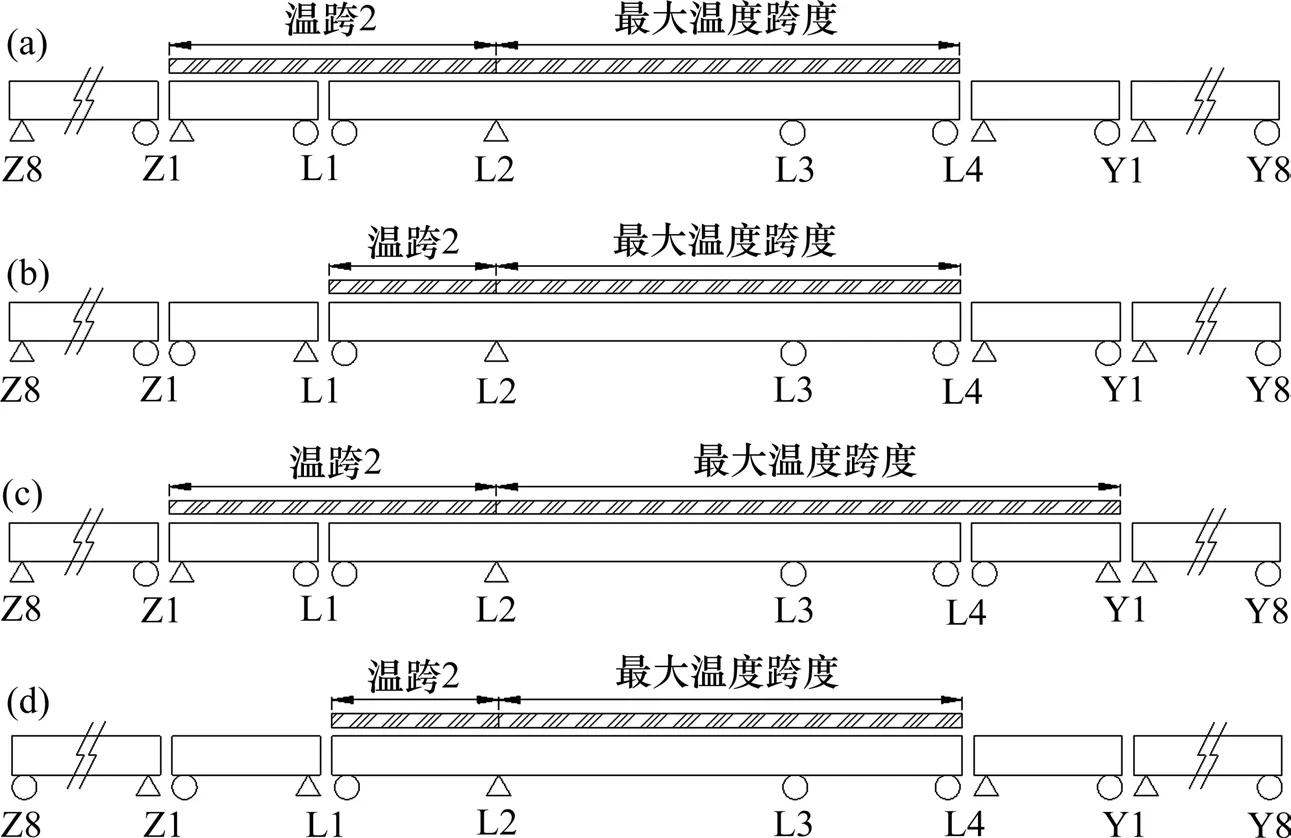
图11 支座非顺序布置方案Fig.11 Support non-sequential layout scheme

图11 中，工况1 为线路纵坡为正条件下支座默认布置方式，最大温度跨度为连续梁主跨与边跨之和。在工况1 的基础上，工况2 将连续梁左侧(小里程)相邻一孔跨简支梁固定支座调换位置，减小了一孔跨简支梁温度跨度；工况3将连续梁右侧(大里程)相邻一孔跨简支梁固定支座调换位置，增大了一孔跨简支梁温度跨度；工况4将连续梁左侧(小里程)简支梁活动支座均放置在左端，软土地基时设计大幅度减小Z8桥台承受的水平力。

在图12(a)可以看到，由于最大温度跨度相同，工况1 与工况2 钢轨应力分布基本一致。工况3 由于温度跨度最大，其最大钢轨应力发生于Y2 活动支座处。工况4中，由于连续梁左侧简支梁活动支座全部设置在左端桥台处，大幅增加了左侧钢轨受力，在左桥台Z8 处应力最大，并向连续梁右侧传递直至连续梁L2制动墩活动支座处达到峰值。

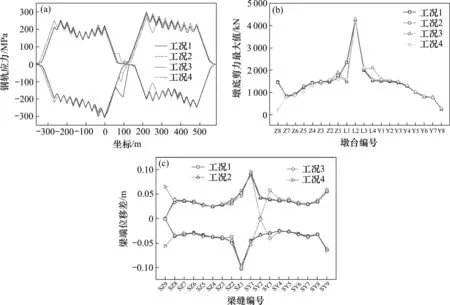
图12 支座非顺序布置对梁轨系统地震响应影响Fig.12 Influence of support non-sequential layout on seismic response

图12(b)中，最大墩底剪力变化较小基本一致，均发生于连续梁制动墩处。考虑支座布置差异，工况3 中温跨最大，因此L4 和Z1 墩受较大水平力作用。另外，由于工况4中简支梁活动支座设置在最左侧桥台处，钢轨承受大部分纵向力，因此可以看到Z8 桥台所受水平力最小，这与设计理念是相符的；图12(c)中，最大梁端位移差均发生于连续梁两端活动支座的SZ1 和SY1 梁缝处，工况3中，由于Y1 墩均设置固定支座，故此处SY2 梁缝处梁端位移差基本为0，相对应的L4 和Z1 墩受较大水平力作用。与墩台受力相对应，工况4 中SZ9桥台处由于设置活动支座，故梁缝位移最大并达到0.07 m，但落梁、碰撞几率仍较小。

地震作用下支座非顺序布置影响的结构温度跨度仍是影响梁轨系统互制受力的控制性因素之一。当桥台路基状态良好时，建议按照工况2支座布置，均衡梁轨受力与变形。当桥台路基地质条件较差时，建议按照工况4支座布置，大幅减小桥台受力，但应注意桥台大位移变形增加了路桥过渡段轨道搭板结构损伤概率，不利于结构形位的保持。

5 结论

1) 相对于在连续梁边跨及相邻一孔跨简支梁上铺设小阻力扣件的方案，建议仅在连续梁范围内铺设小阻力扣件，使墩顶位移、梁轨相对位移、梁端位移及结构受力均保持在较小限度内。

2) 钢轨伸缩调节器是无缝线路中薄弱环节，会引起轨道的不平顺，降低运营舒适度，应尽量减少调节器的使用。当确需设置调节器时，建议仅在连续梁活动端设置，必要时可在对侧边跨及相邻一孔跨简支梁同时铺设小阻力扣件。

3) 梁轨系统地震分析中，相邻简支梁桥墩刚度相差不大时可按连续梁两侧接8跨简支梁进行地震作用简化计算。连续梁跨度超过(60+100+60) m后，地震动时落梁现象几率增加，钢轨受力大幅增加。

4) 连续梁和简支梁的支座布置原则为尽量减小温度跨度和桥墩受力。桥台路基状态良好时，可将相邻简支梁固定支座靠近连续梁布置，均衡梁轨结构受力与变形。当桥台路基地质条件较差时，可将简支梁活动支座设置在桥台处，大幅减小桥台受力。