密实状态下拱桥管内混凝土超声波波速的时变规律及多因素模型

凌干展，解威威，秦大燕，唐睿楷，曹璐，刘祥

(广西路桥工程集团有限公司，广西 南宁 530200)

钢管混凝土拱桥具有优良的力学、施工性能以及经济优势，是铁路工程中跨越山区峡谷的重要桥型，位于拉林铁路上的世界最大跨度铁路钢管混凝土拱桥—藏木雅鲁藏布江特大桥也已建成通车。然而，受施工灌注质量、混凝土收缩徐变、温度升降等问题的影响，钢管混凝土拱桥易出现脱粘脱空等内部缺陷情况[1-3]。当前，超声波无损检测是应用最为广泛的定量描述管内混凝土灌注密实程度的技术手段[4-5]。因此，研究建立密实状态下的钢管混凝土拱桥超声波波速预测模型，对于钢管混凝土拱桥密实性能评估具有重要意义。目前，基于超声波法的钢管混凝土结构密实性能研究已受到国内外学者的广泛关注，并建立了多种类型的计算模型。其中，张涛等[6]基于现场实测数据，通过规范提出的数理统计方法[7]分析确定了超声波波速的均值和标准差，但是上述方法只能从平均意义上描述核心混凝土的密实程度。为了克服上述缺陷，LIU 等[8]通过理论推导建立超声波波速与密实特征参数之间的函数关系式。虽然一定程度上解决了对样本数据的依赖问题，但是该模型忽略了核心混凝土非均质特性的影响[9-10]，导致实际工程应用受到限制。研究分析表明，超声波在核心混凝土中的传输机制主要受水泥石密度、骨料类别、孔隙等因素的影响[11]。为此，ZHANG等[12-15]分别采用线性、非线性、指数、幂函数等函数形式来描述混凝土抗压强度和超声波波速之间的定量关系，然而模型均没有考虑检测龄期的影响，从而无法合理描述管内混凝土密实演化的时变特性[16]。针对该问题，BADACHE 等[17]在上述模型的基础上建立了考虑混凝土抗压强度和检测龄期影响的超声波波速预测模型，但是该模型仅适用于龄期为28 d 和90 d 的情况，而对于规范要求的检测龄期以及成桥运营后全生命周期监测具有一定的局限性[18]。综上可知，虽然国内外学者围绕密实超声波波速计算模型开展了广泛的研究，但是现有的研究成果大都局限于核心混凝土密实性评估，而在实际工程中，钢管拱肋拼接节段处往往同时存在外钢管、加劲板、法兰盘、内衬管等复杂钢-混组合结构，导致该区域易出现脱粘脱空等不密实现象[1]。因此，有必要进一步研究一种能够合理考虑混凝土抗压强度、检测龄期和钢-混组合结构类型综合影响的超声波波速预测模型，从而量化描述钢管混凝土拱桥灌注成桥后的密实特性及演化规律。鉴于此，本文首先通过搜集遴选5座钢管混凝土拱桥现场检测数据以及584组钢管混凝土试验数据，建立了超声波波速的试验数据库。然后通过对试验数据的分析，研究确定了检测龄期和钢-混组合结构类型对超声波波速的影响规律，并通过引入时间系数和钢-混组合影响系数修正密实状态下超声波波速的多因素模型，进而基于2阶段回归分析法确定了待定拟合参数取值，从而建立一种能够综合考虑混凝土抗压强度、检测龄期和钢-混组合特性影响的钢管混凝土拱桥密实超声波波速多因素时变模型。最后通过与现有模型、试验数据和现场检测数据对比分析，验证了该模型的有效性。

1 考虑时变特性对超声波波速的影响规律分析

1.1 超声波检测数据库建立

本文以中国境内多座钢管混凝土拱桥为研究原型。由于受施工灌注工艺、混凝土收缩徐变、温度升降等问题的影响，核心混凝土有可能出现脱粘、脱空等内部缺陷情况[19]，严重影响钢管混凝土结构的使用性能。因此，为保障桥梁结构的安全性和稳定性，利用超声波无损检测技术对灌注后的钢管混凝土拱桥展开密实性能评估。超声波检测钢管混凝土的基本原理是在钢管外径的一端利用发射换能器辐射高频振动，经钢管圆心传向钢管外径另一端的接收换能器[20]。此外，根据管内混凝土施工工艺特点及拱肋节段吊装作业平台分布情况，对拱脚、各节段拼接以及拱顶位置开展检测。如图1所示。

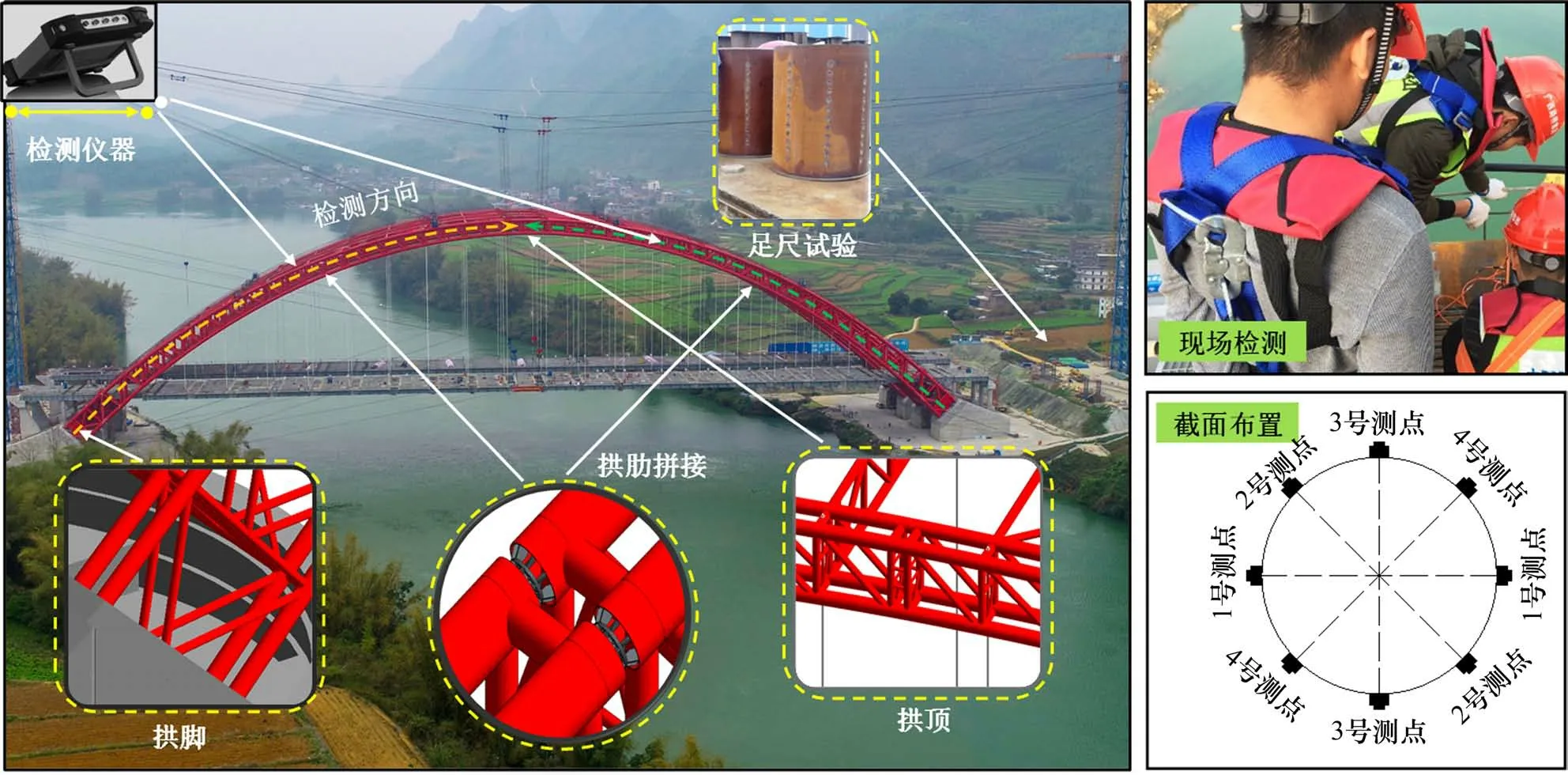
图1 超声波检测分布示意图Fig.1 Schematic diagram of ultrasonic detection distribution

在此基础上，本次试验共设计并制作了3个钢管混凝土足尺试件，如图1所示。待混凝土浇筑完成后，采用RSM-SY8 非金属超声检测仪分别对2～28 d 龄期的钢管混凝土试件进行检测。此外，为了合理分析超声波波速的关键影响因素，获取更加丰富平衡的样本数据，本文从国内外多个国家和地区搜集遴选了496 组超声波检测试验数据，建立了超声波检测数据的标准数据库，基本信息见表1 所示。由表1 可知，混凝土抗压强度的范围在17.10～81.45 MPa 之间，检测龄期在1～3 650 d之间，覆盖范围较广，说明所搜集的试验数据具有较好的代表性。

表1 584组超声波检测数据的基本信息Table 1 Basic information of 584 groups of ultrasonic test data

1.2 检测龄期对超声波波速的影响规律分析

根据规范GB 50923—2013[18]的要求，需对管内混凝土灌注后7 d 和28 d 以及验收前的质量进行检验。对此，为了研究检测龄期对超声波波速的影响规律，基于表1 文献[11,22,24,26-28]中1～120 d 的试验数据，分析检测龄期对超声波速的影响规律，如图2 所示。由图2 可知，随着检测龄期的增大，超声波波速在短龄期内增加较快，但随着检测龄期的延长，超声波波速的增长速度逐渐放缓，并趋于平稳。究其原因在于，核心混凝土主要由水泥石、骨料、孔隙等介质构成，由于各介质间的声阻抗差不同，使得超声波在混凝土结构中的传播路径复杂多变，整体上可分为反射、透射和绕射3种现象。其中，超声波在各介质间的反射率和透射率可描述为[11]：

式中：R和T分别为超声波从介质1垂直进入介质2时的反射率和透射率；Z1和Z2分别为介质1和介质2 的声阻抗值。具体表现为：当超声波在固体介质与空气介质之间传播时，由于固体介质与空气介质的声阻抗差较大，则超声波传输方式以绕射为最短传播路径，从而增加了超声波传递的路线长度。另一方面，随着水泥和矿物掺合料二次水化等过程不断发展，混凝土孔隙不断被水化产物填充而趋于密实，导致混凝土的密实性逐渐提高且呈现早期发展快后期发展慢的趋势，则超声波传输路径从原先的绕射转变为透射，从而提升了超声波的传输速度。基于上述分析可知，可以利用倒数函数来描述超声波波速(简记为UPV)先快速增加后逐渐放缓并趋于稳定的时变特性：

式中：UPVt为考虑检测龄期影响的超声波波速值，m/s；υ和ε均为拟合系数；t为检测龄期，d。

2 超声波波速多因素时变模型

2.1 基于混凝土抗压强度的超声波波速单因素模型选择分析

陈正等[11-12]的研究表明，核心混凝土主要由水泥石、骨料等介质构成，根据波动理论[11]，超声波波速与固体介质的弹性模量、泊松比和密度之间存在一定关系。由于不同固体介质的弹性模量、泊松比和密度等存在差异性，使得超声波在不同固体介质中的传输速度有所不同，则整体超声波波速受水泥石、骨料等固体介质的影响。实际上，混凝土抗压强度性能正是水泥石、骨料等微观结构的宏观体现。针对该问题，国内外学者相继提出了线性[11,30]、指数[13-14]、对数[12]、非线性[12,15]、幂函数[15]等多种函数形式的模型来描述混凝土抗压强度和超声波波速之间的关系。

线性型：

指数型：

对数型：

非线性型：

幂函数型：

式中：fc为核心混凝土28 d 抗压强度；UPVc为核心混凝土的超声波波速，m/s；ai(i=1,2,3,…,11)为拟合参数。其中，拟合参数ai的取值与水泥石、骨料类型等因素有关，不失一般性地以线性、指数、对数、非线性和幂函数为例，利用文献[11,21-23,26-28]中28 d 的试验数据，对比分析上述5 种模型的预测精度和变化规律，如图3 所示。由图3可知，随着超声波波速的增加，线性模型、指数模型、对数模型、非线性模型、幂函数模型的计算值均逐渐增加。其中，当fc>50 MPa 时，指数、对数和幂函数模型的计算值与试验值的吻合度较差，且明显呈低估现象；当fc<50 MPa时，非线性模型的计算值与试验值的吻合度较差，且明显呈低估现象，此外，非线性模型的计算值随着超声波波速的增加出现斜率先递减后递增的趋势，与超声波波速的实际工程规律不符；相比之下，线性模型能够更加合理地描述核心混凝土与超声波波速之间的相关特性，因此，可以将式(3)改写为：

图3 基于不同试验数据的超声波波速预测模型对比分析Fig.3 Comparison and analysis of ultrasonic pulse velocity model based on different data

式中：UPVfc为考虑混凝土抗压强度影响的超声波波速值，m/s；α和β为拟合系数。

2.2 考虑钢-混组合结构特性的耦合影响

在实际工程中，钢管混凝土拱桥拱肋拼接段等区域往往同时存在法兰盘、加劲板、内衬管等管内钢结构，导致该区域易出现脱粘脱空等不密实现象[1,28]。鉴于此，有必要分析复杂钢-混组合结构下超声波波速的演化规律，如图4 所示。由图4可知，超声波在拱肋拼接段截面传播路径上可能存在外钢管、加劲板、法兰盘和内衬管等钢-混组合结构类型。此外，根据陈正等[11]研究表明，当假定结构为均值材料时，基于波动方程理论可知，整体超声波波速由钢-混组合结构的弹性模量、泊松比和密度共同决定。基于上述理论分析，可建立考虑复杂钢-混组合结构的整体超声波波速理论模型，则整体超声波波速的最短传输时间(也称为首波声时)T可表示为：

式中：Ts为超声波经过外钢管、法兰盘、加劲肋、内衬管等钢结构的时间；Tc为超声波经过核心混凝土的时间；UPVs和UPVc分别为超声波在钢结构和核心混凝土中的超声波波速，m/s；Ss和Sc分别为超声波在钢结构和核心混凝土的传播路径，m；在此基础上，可以建立考虑复杂钢-混组合结构的整体超声波波速理论模型：

式中：UPVη为考虑复杂钢-混组合结构影响的超声波波速，m/s；S为钢管混凝土结构外直径，m；η为钢-混组合结构影响因子：

需要说明的是，由于核心混凝土自身材料的多样性以及钢-混组合结构所处环境的复杂性，基于直线传播理论所建立的式(10)模型具有一定的局限性。针对上述问题，利用1.1 节已收集的钢管混凝土拱桥现场检测数据，研究分析混凝土、钢管混凝土以及内嵌加劲板、法兰盘和内衬管的钢管混凝土截面类型（分别简记为C，CFST，CFST+SP，CFST+F 和CFST+LT）对超声波波速的影响规律，如图5所示，其中，试验值和拟合曲线分别简记为TD 和FC。由图5 可知，当钢-混组合结构类型不同时，对应超声波波速拟合曲线各不相同，且随着检测截面钢结构厚度占比的增加，超声波波速近似呈线性增大趋势。由此可见，钢-混组合结构类型对超声波波速变化规律具有显著的影响。因此，在式(8)的基础上，可以将超声波波速计算模型修正为：

图5 钢-混组合结构类型对UPV的影响Fig.5 Influence of steel-concrete composite structure type on UPV

式中：UPVfc,η为考虑混凝土抗压强度和钢-混组合结构影响的超声波波速，m/s，以下类似之处不再重复说明；η为钢-混组合结构的影响因子，反应钢-混组合结构类型对超声波波速作用规律的影响。

2.3 多因素时变模型及待定参数的确定

根据上述分析可知，超声波波速UPV与混凝土抗压强度fc之间近似成呈线性关系。同时，采用倒数模型可以较好地描述UPV的时变特性。在此基础上，合理考虑钢-混组合结构类型对UPV的耦合影响。鉴于此，结合式(2)和式(12)，可以进一步建立钢管混凝土拱桥密实状态下的超声波波速多因素计算模型UPVfc,t,η：

需要说明的是，式(13)中拟合参数α，β和ε是反映UPV与主要影响因素相关关系的模型参数，而影响因子η是反映钢-混组合结构类型对超声波波速演化规律的修正系数，与拟合参数α，β和ε类型不同。因此，本文采用2 阶段拟合方法确定式(13)中的4 个待定参数，计算步骤如下：首先假定钢-混组合结构的影响因子η为1，然后基于表1 中584 组超声波检测数据，采用多元非线性分析法，可以拟合得到α，β和ε的取值分别为8.81，4 411和5.20。根据拟合得到的α，β和ε代入式(13)可改写为：

在此基础上，分别基于1.1 节已收集的226 组CFST，81 组CFST+SP，48 组CFST+F 和75 组CFST+LT 的钢管混凝土拱桥超声波检测数据，采用多元非线性分析法进一步确定式(14)中的待定参数η，可以得到CFST，CFST+SP，CFST+F 和CFST+LT 组合截面所对应的钢-混组合结构的影响因子η的取值分别为1.12，1.46，1.61和1.23。

3 对比验证分析

3.1 模型预测效果的对比分析

为了对比验证本文模型的适用性和有效性，选取CECS21:2000模型[7]、文献[30]和文献[17]模型进行对比分析。同时，基于已收集的多座钢管混凝土拱桥超声波检测数据为例，利用本文提出的模型和上述3 个模型，分别预测检测龄期为2，7，14和28 d的UPV，并与检测数据进行对比，如图6所示。由图6 可知，CECS21:2000 模型的散点大都落在±5%线之外，且随着检测龄期变化规律不明显，说明CECS21:2000 模型预测精度较差；另一方面，由图6(a)和图6(b)可知，当检测龄期为2 d和7 d 时，文献[30]模型的散点大部分落在±5%线之上，且明显呈高估现象。而文献[17]模型的散点大部分落在±5%线之下，且明显呈低估现象；同时，由图6(c)和图6(d)可知，当检测龄期为14 d 和28 d 时，文献[30]和文献[17]模型的散点部分落在±5%线之下，且明显呈低估现象。相比之下，本文模型的散点大都落在±5%范围内，充分说明本文模型的UPV预测值与检测数据吻合较好。究其原因在于CECS21:2000 模型基于检测数据，通过数理统计方法确定的超声波波速临界值只能从平均意义上描述核心混凝土的密实程度；其次，文献[30]并未考虑检测龄期和钢-混组合结构类型对超声波波速作用规律的影响；再次，文献[17]虽然考虑了检测龄期的影响，但是该模型仅适用于龄期为28 d 和90 d 的情况，且并未考虑钢-混组合结构类型的耦合影响。由此可见，与现有模型相比，本文提出的模型计算精度较高，具有较好的适用性。

图6 超声波波速预测值与检测数据的对比分析Fig.6 Comparison between predicted and tested UPV

3.2 考虑钢-混组合结构特性的合理性分析

为了进一步验证本文模型对于拱肋拼接段截面的超声波波速预测效果，基于1.1 节中没有用于参数分析的拱肋拼接段检测数据为例，采用本文考虑钢-混组合结构特性影响(简记UPV-η)和不考虑钢-混组合结构特性影响(简记为UPV)计算所得到的预测值与检测数据对比，如图7 所示。由图7可知，UPV模型虽然在一定程度上满足拱肋拼接段超声波波速预测的变化趋势，但均出现不同程度的低估现象。其中，当检测截面存在加劲板和法兰盘时低估现象较为明显，其对应的拟合优度分别为0.61和0.53。而对于检测截面内存在内衬管时低估现象相对不明显，其对应的拟合优度为0.78。由此可见，加劲板、法兰盘和内衬管等复杂钢-混组合结构的存在对超声波波速具有不同程度的提升作用。总体而言，UPV-η模型的预测结果与检测数据最为接近，再次验证了该模型对钢管混凝土拱桥全截面检测评估具有较高的计算精度和适用性，为钢管混凝土拱桥全生命期健康监测提供了科学依据。

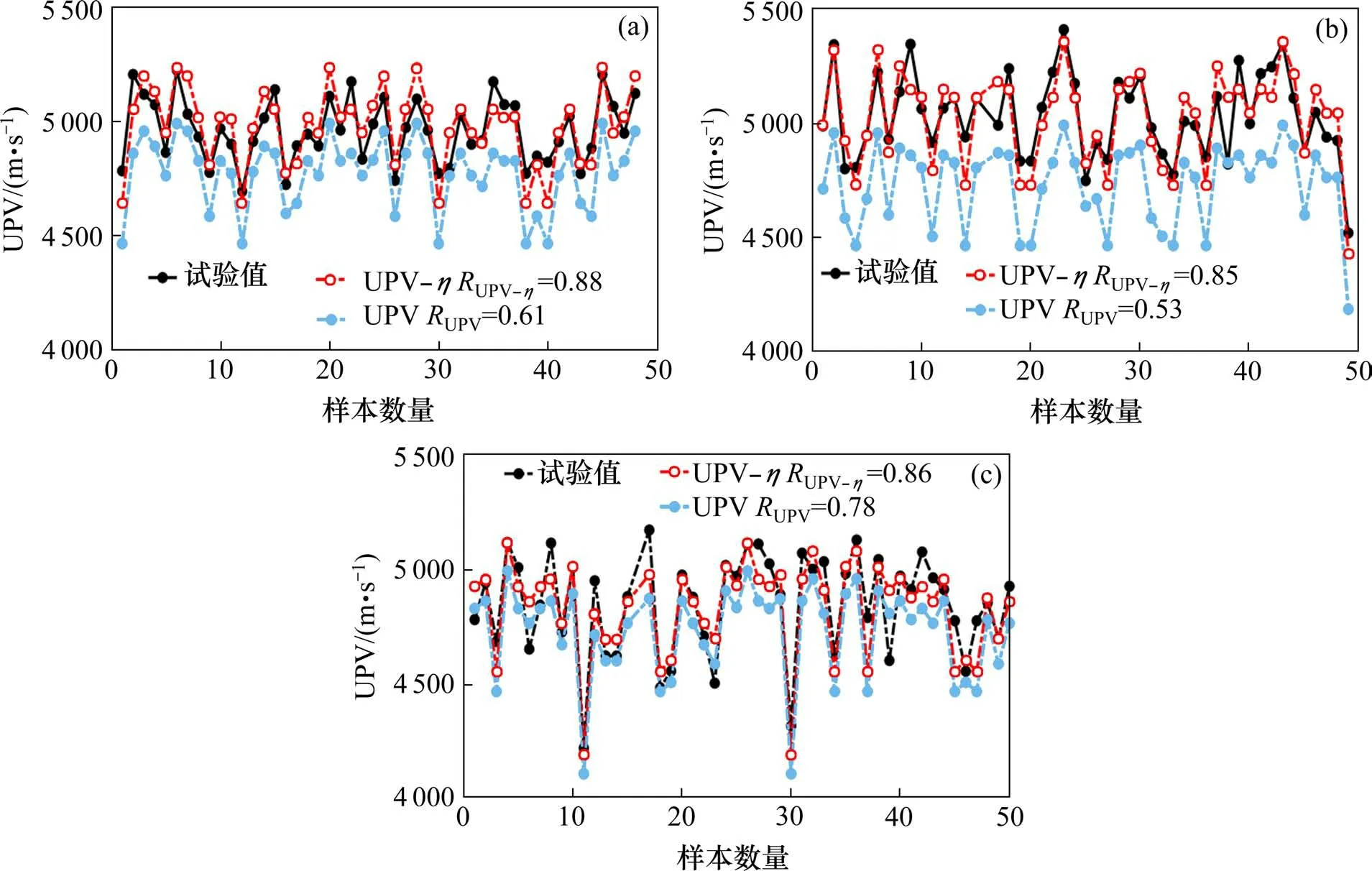
图7 模型预测值与拱肋拼接段检测数据的对比分析Fig.7 Comparison between predicted UPV and arch rib splicing position tested data

4 结论

1) 当检测龄期较短时，超声波波速的时变特性影响较大，且随着检测龄期增加，超声波波速的时变特性影响逐渐减小。对此，采用倒数模型可以合理地描述超声波波速先快速增加后逐渐放缓并趋于稳定的时变规律。

2) 与指数、对数、幂函数和非线性等函数形式模型相比，采用线性模型能够更加合理地描述超声波波速与核心混凝土抗压强度之间的相关特性。

3) 与其他测区相比，当测区截面内存在加劲板、法兰盘、内衬管等复杂钢-混组合结构时，超声波波速随着截面钢结构厚度占比的增加近似呈线性增大趋势。

4) 与现有的模型相比，所建立的多因素时变模型不仅构建了多特征参数与超声波波速之间的耦合关系，而且对钢管混凝土拱桥全截面检测评估具有较高的计算精度和适用性。