考虑桩-桩剪切作用的连锁墙时空变形分析

成怡冲 ，张日红，王奎华 ，艾智勇，吴才德

(1.浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058；2.浙江大学 软弱土与环境土工教育部重点实验室，浙江 杭州 310058；3.宁波中淳高科股份有限公司，浙江 宁波 315000；4.同济大学 地下建筑与工程系，岩土及地下工程教育部重点实验室，上海 200092；5.浙江华展工程研究设计院有限公司 浙江 宁波 315012)

传统基坑围护结构多为现场浇筑施工，存在着高污染、高能耗及质量不易控制等问题，因而具备绿色低碳属性的各类预制装配式结构正逐步在基坑工程中得到应用[1-2]。连锁混凝土预制桩[3](以下简称“连锁桩”)是一种截面轮廓近似方形，左右两侧各带2个半椭圆形凹槽，采用离心工艺成型的先张法预应力混凝土空心桩，如图1所示。连锁桩连排沉桩后可在地下形成连续墙体(以下简称“连锁墙”)，而相邻两桩侧面凹槽合拢后形成完整椭圆孔，称为“连锁止水孔”。通过对连锁止水孔进行注浆，可达到桩桩相扣和止水的双重作用。作为一种新型地下空间装配式结构，连锁墙技术的研究尚处于起步阶段。黄强等[4]介绍了连锁桩的生产与施工工艺，并通过基坑实验段验证了该技术的可行性和安全性。陈伟[5]针对上述实验段采用惯性矩不变原则将连锁墙换算成实心墙体后进行平面应变条件下的围护结构设计，但实测结果表明连锁墙变形存在明显的空间效应。不同于离散桩体构成的围护墙，连锁止水孔中注浆体的存在使相邻连锁桩之间产生联系，并可能对连锁墙的空间受力与变形产生影响，但目前关于连锁墙界面剪切特性及其对连锁墙整体性能影响的研究还未见报道。另一方面，在城市地下空间开发过程中，基坑紧邻管线、隧道等重要建(构)筑物的情况愈发普遍[6]。为保障基坑周边环境安全，提升基坑围护结构整体变形预测的准确性具有重要意义。目前，国内普遍采用基于弹性地基梁理论的全量法或增量法对基坑围护结构进行计算，其中增量法可考虑基坑开挖与设撑工况，相比于全量法更为合理。在增量法基础上，黄彪等[7]建立了非极限土压力和围护结构侧移的耦合关系，通过将非极限土压力模型嵌入弹性地基梁法的控制方程，实现了对开挖全过程围护墙受力变形的分析；刘成禹等[8]认为增量法中的荷载增量除了土压力增量和挖除土体弹性抗力释放的反力增量2部分外，还应包括开挖面以下土体因开挖面下降、水平抗力系数降低等引起的土体弹性抗力部分释放的反力增量，并基于此对增量法进行了改进；周勇等[9]则同时考虑了位移-土压力关系及被动区土体因开挖导致的抗力系数变动，将改进后的增量法应用于桩锚支护结构的计算。上述改进方法使基坑围护结构的计算结果更接近工程实际，但仍局限于二维平面应变假定，难以分析基坑变形的时空效应[10-11]。为更合理地预测连锁墙的受力与变形，有必要结合其自身结构特点及基坑变形的时空效应规律提出相适应的设计计算方法。本文首先开展了针对连锁墙中桩-桩界面的剪切试验，得到了桩-桩界面的受力变形规律，并推导出基于桩-桩相互作用的连锁墙刚度计算公式。通过考虑连锁墙刚度、位移及时间因素的影响，对二维增量法进行了改进，提出一种考虑时空效应和桩-桩剪切特性的连锁墙计算方法。最后通过计算结果与工程实测结果的对比，验证了方法的合理性。

图1 连锁混凝土预制桩Fig.1 Concrete precast piles for chained wall

1 连锁墙中桩-桩界面剪切试验

1.1 试验方案

如图2 所示，试验采用特制夹具夹紧3 块代表连锁桩的混凝土试件构成连锁试件，然后对中间试件加载以获取荷载-位移曲线。竖向加载装置采用电子伺服拉力试验机(型号WLD-10000，见图3)。单个混凝土试件的基本尺寸为150 mm×150 mm×300 mm，剪切面考虑为600 mm 边长连锁桩按2︰1 缩尺，即其中150 mm×300 mm 的一面。试件剪切面上设计直径为50 mm 的半圆形凹槽以模拟连锁止水槽。混凝土材料符合相关规范要求，强度标号为C60。混凝土试件在模具中浇筑完成后放入养护室按标准养护28 d。

图2 用于剪切试验的混凝土试件Fig.2 Concrete specimens used for shear test

图3 中间混凝土试件竖向加载Fig.3 Intermediate concrete specimen loaded vertically

连锁桩施工后，相邻连锁桩之间一般会存在一定的空隙(夹泥)，可以认为两桩间接近光滑接触状态，故本次试验主要模拟两桩不接触但两者之间有注浆体的情况。实际工程中，连锁止水孔有压注浆后砂浆硬化回缩会导致接触面压力的降低，考虑到试件制作中较难实现有压注浆，故试验中不考虑接触面法向压力的影响，但通过夹具约束试件法向位移。连锁止水孔注浆在3块试件夹紧后进行，相邻试块间采用等厚塑料板分隔，并保证注浆后观测面平整，注浆体截面轮廓清晰。注浆完成后在自然条件下进行28 d 养护；同时，注浆体材料做边长70.7 mm立方体试块并在养护后进行强度试验。注浆体经水泥砂浆试块抗压试验分别达到了M20 和M30 强度等级，对采用这2 种等级砂浆作为注浆体的连锁试件分别进行2 组平行试验。

试验步骤如下：1) 连锁试件放置于伺服机上，静置3 min；2) 中部试件上方放置钢垫块，伺服机压头下移至钢垫块；3) 采用位移控制加载方式进行竖向加载，加载速率1.0 mm/min，当竖向位移达到10～12 mm 时，试验终止，获取计算机自动采集的荷载-位移曲线数据；4) 记录界面破坏情况，伺服机压头上移，移出连锁试件；⑤改变试验工况，重复上述步骤1～4进行剪切试验。

1.2 试验结果分析

桩-桩界面最终受剪破坏情况见图4，采用不同注浆材料情况下获得的剪切力与剪切位移关系曲线见图5。由曲线变化情况可知界面剪切变形可大致分为5个阶段：1) 弹塑性阶段，由界面受力至凹槽处裂缝产生，该阶段剪力与位移基本为线性相关；2) 凹槽开裂阶段，凹槽面剪应力达到混凝土试块与注浆体之间的黏结应力，凹槽面产生裂缝，该阶段位移增量很小但剪力显著下降，呈现脆性破坏；3) 强化阶段，凹槽面裂缝贯通后，界面剪力转由注浆体承担；4) 注浆体开裂阶段，注浆体承受的剪应力达到其抗剪承载力，中心截面受剪开裂，该阶段同样为脆性破坏；5) 滑移阶段，注浆体剪坏后，注浆体的位变重新形成受剪面，加之粗糙剪切面还可提供一定的摩阻力，故试件未直接破坏。

图5 不同注浆体时的剪力与位移关系Fig.5 Shear force-displacement relationship under different grouting bodies

采用不同等级砂浆作为注浆体时，砂浆强度等级越高，第1阶段的界面剪切刚度越大，最终的剪力峰值也越大，但剪力峰值对应的位移相差不大；此外，采用M30 砂浆作为注浆体时，凹槽面开裂发生较早，凹槽面开裂至注浆体开裂过程中仍可承受较大的剪力增量，而对于采用M20 砂浆的注浆体，注浆体开裂紧跟凹槽面开裂。一般认为桩间界面开裂即意味着止水失效。从试验结果看，提高注浆体的砂浆强度等级有助于提高界面剪切刚度，但可能降低其止水性能。因此，具备高黏结性能和强度的注浆体材料[12]有待进一步研发。

存在注浆体情况下连锁桩间的切向行为较为复杂，但基本符合理想弹-塑性模型特点。为方便对上述界面特性的利用，将图5 的剪力-位移曲线转化为图6 所示的剪切应力-相对剪切位移(τ-ΔU)曲线。考虑到界面剪力最终由注浆体承担，转换时界面面积按注浆体中心截面面积考虑，弹性段斜率为阶段1线性拟合后的斜率除以界面面积，而峰值剪应力按阶段5初始时的剪力除以界面面积确定。转换后的界面剪切特性参数见表1。由表1 可知，M30 砂浆的界面峰值应力τmax和界面剪切刚度χ约为M20 砂浆的1.4 倍，但两者峰值应力对应的临界位移较为接近。

表1 桩-桩界面剪切特性参数Table 1 Shear characteristic parameters of pile-pile interface

图6 桩-桩界面剪应力与相对位移关系Fig.6 Relationship between shear stress and relative displacement of pile-pile interface

2 考虑桩-桩作用的连锁墙刚度

图7 展示了由N根连锁桩构成的连锁墙平面，对于其中的第j根连锁桩采用两节点梁单元进行模拟。根据有限元理论及桩的受力情况，单根连锁桩的刚度矩阵方程可表示为：

图7 连锁平面示意图Fig.7 Schematic diagram of plane of chained wall

式中：和U j分别为第j(j=1～N)根桩的刚度矩阵和节点位移向量；和分别代表第(j-1)根桩和第(j+1)根桩对第j根桩的作用力的等效节点力向量，当不存在相邻桩或邻桩与第j根桩无接触时，和可取同维数的零向量；F j代表作用在第j根桩上的坑外水土压力等其他作用力的等效节点力向量。

图8示意了相邻连锁桩同一深度位置的桩单元之间的相互作用关系，其中和分别代表第(j-1)根桩、第(j+1)根桩对第j根桩的作用力。假定上述作用力在桩单元上线性分布，则有[13]：

图8 相邻桩单元相互作用示意图Fig.8 Schematic diagram of interaction between adjacent pile elements

式中：Tj为根据两节点单元插值关系获得的节点位置处作用力强度与等效节点力的转换矩阵，可由单元转换矩阵根据有限元方法组装得到，其中，L(e)代表节点单元的长度；z*为两节点单元的局部坐标；N为插值函数矩阵；和分别为和在第j根桩各节点位置的强度构成的向量。考虑到连锁墙中相邻两桩之间的作用力大小相等且方向相反，则有如下关系：

采用如图6所示的界面切向行为模型，可得如下关系：

式中：Δ为节点i位置处相对位移的绝对值，可从ΔU获得。

将式(3)和式(4)代入式(2)，并将所有连锁桩进行整体考虑，可得：

式中：

将式(1)中的单根连锁桩扩展为连锁墙并将式(6)代入，可得：

3 考虑时空效应的连锁墙计算模型

3.1 计算假定

根据增量法原理[7]，针对连锁墙基坑开挖过程中的某一工况，有：

式中：上标a(a>1)代表第a个工况；该工况下的围护体系总刚度由3 部分构成，其中为该工况下连锁墙总刚度矩阵，按式(7)求解；和分别为该工况下支撑和被动区土体的总刚度矩阵，按规范[14]求解，其中与m值(土的水平反力系数的比例系数)相关；δU a和δF a分别代表该工况的位移增量和荷载增量；Pa和δPa分别代表该工况的土压力和土压力增量；则为该工况的开挖侧土体刚度变化量；另外，U0和P0取相应维数的零向量。

荷载增量δF a的计算是增量法的关键内容，由式(8(b))可知，它包括土压力增量和土抗力释放增量2部分，而它们均会随着时间的变化而变化。为便于考虑时间效应对荷载增量的影响，本文将基坑施工工况分为2种类型，一种是土方开挖至支撑底(可考虑一定超挖)或坑底的开挖工况；另一种是支撑、底板(垫层)施工至形成强度前的暴露工况。根据基坑施工实际，这2类工况一般交替出现。另外，假定土压力随时间持续变化，与具体工况无关；而被动区土体由于开挖的扰动而发生显著蠕变，蠕变变形发生在暴露工况。基坑变形的三维空间效应主要体现在坑角效应[15]，大量工程实测和数值模拟结果显示，越靠近基坑角部，基坑的变形越小，因此可假定角点处的位移为0[16]。

3.2 土压力计算

如图9所示，作用在围护墙上的土压力由静止土压力P0发展为极限土压力Pcr需要以一定的土体变形量为前提，而相关研究亦表明考虑非极限土压力可获得更合理的计算结果[7]。张常光等[17]基于Sigmoid 函数提出了实用的位移-土压力拟合新公式。在此公式基础上，根据非静止土压力随时间增加将重新趋于静止土压力的实际[18]，本文采用的土压力计算公式为：

图9 土压力随位移变化曲线Fig.9 Curve of earth pressure varying with displacement

式中：P为当前时间t和位移U下的非极限土压力；μ为土压力蠕变系数，其在开挖后期较为稳定，可取10-5/d[18]；极限位移Ucr和拟合参数λ按文献[17]取值。

此外，基坑开挖后坑外土体不均匀变形将引发拱效应，并影响土压力的空间分布。本文通过将土压力按空间效应系数κ进行折减的方式近似考虑土压力的空间效应，κ的计算参见文献[19]。

3.3 土抗力计算

对于被动区土体蠕变问题，将m值表示为时间的函数并认为它与土体弹性模量随时间的变化规律一致[20]。采用图10 所示的Merchant 黏弹性模型模拟土的应力应变关系，则有：

图10 Merchant模型示意图Fig.10 Schematic diagram of Merchant model

式中：t0和Δt分别表示暴露工况的起始时间和已持续时间；m(t)为t时刻对应的土的m值；α=E0/E1，其中E0和E1分别对应Merchant 模型中2 个虎克弹性体的弹性模量；β=E1/η，其中η为土的黏滞系数。

根据式(10)可求出暴露工况的Ks，代入式(8(c))可得土抗力释放增量。需要指出的是，因开挖扰动和暴露导致开挖面以下土体蠕变的范围是有限的，若考虑开挖面以下至围护墙底范围内的土体均发生蠕变显然将夸大时间效应的影响，故实际产生蠕变的深度范围可取开挖面以下3～5 m[14]，施工扰动大或暴露时间长时取大值。

3.4 增量法迭代计算

因式(4)和式(9)与对应工况下的墙体侧移量相关，故式(8)需通过迭代的方式进行求解。迭代计算的基本思路为：1) 根据上一工况a-1 的最终计算结果确定本工况a初始的时间、连锁墙侧移及刚度参数；2) 将上述参数代入式(4)，式(8)～(9)，得到荷载增量和围护体系刚度，并由此计算对应的连锁墙侧移；3) 将此连锁墙侧移与初始的连锁墙侧移进行对比，若两者误差满足精度要求则进行下一工况运算；若不满足精度要求，则以本次运算得到的连锁墙侧移及刚度参数为初始值，时间参数不变，重新进行第2步，直至满足精度要求为止。图11为增量法迭代计算流程图，其中k为迭代步数。

图11 增量法迭代求解流程图Fig.11 Flow chart of three dimensional incremental method solved by iterative operation

4 案例验证与分析

4.1 项目概况

宁波软土地区某2层地下室基坑，基坑开挖深度H=8.8 m，平面可近似为75 m×80 m 矩形。基坑北侧采用连锁墙，其中连锁桩边长700 mm，EpIp=623.7 MN ∙m2；其余侧采用SMW 工法桩。基坑内设一道半径37 m 的圆环支撑，环梁截面为2.0 m×0.8 m，采用C30 混凝土，圆环支撑的水平刚度按文献[21]方法计算，取为35 MN/m。连锁桩之间采用M20 砂浆双孔注浆，由于连锁止水孔实际为长轴120 mm 短轴90 mm 的椭圆孔，故双孔注浆时接触面长度D取240 mm；切向刚度按第1 节中的试验值取值。此外，坑外荷载按15 kPa 考虑，水土压力计算模式为水土合算。连锁墙围护结构剖面图见图12。

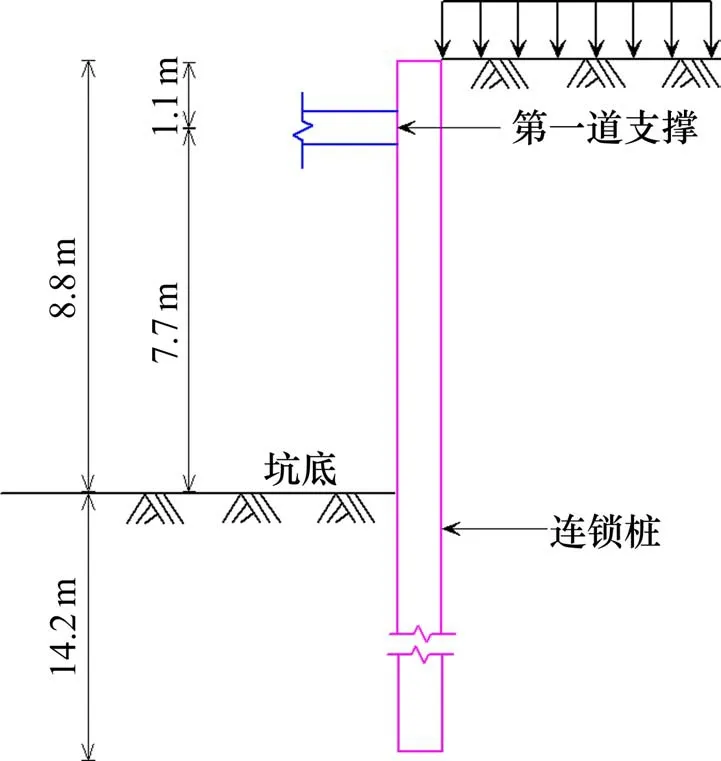
图12 围护结构剖面示意图Fig.12 Schematic diagram of retaining wall section

计算用土层参数见表2。根据当地多个基坑项目反演结果，α取5，β取10-3/d。根据项目实际施工情况，将其简化为4个工况，见表3。

表2 土层参数Table 2 Parameters of soil layers

表3 计算工况Table 3 Calculation cases

4.2 结果分析

连锁墙计算值与实测值的对比见图13，其中监测断面1 和2(以下分别用JC1 和JC2 表示)分别距坑角15 m 和22 m。JC1 位置的墙体侧移显示，工况3 至工况4 过程中连锁墙侧移有显著发展，最大侧移的变形速率达到0.73 mm/d，反映出软土地区基坑变形显著的时间效应。JC1 位置的墙体侧移在不同工况下的计算值与实测值较为吻合，证明采用本文方法考虑基坑变形时间效应是可行的。对比工况4 时的JC1 和JC2 可知，连锁墙侧移越靠近基坑中部变形越大，两监测断面对应的侧移计算值与实测值较为接近，证明本文对连锁墙整体刚度的考虑是合理的。需指出的是，从整体上看本文计算值要略小于实测值且两者差异在墙底位置最为明显，这可能与连锁桩静压沉桩时桩端未能充分压入第3层嵌固层有关；另外，由于本文计算时采用了通过室内试验获得的较理想状态下的桩-桩界面剪切刚度参数，而由于现场施工和养护条件的限制，实际剪切刚度值难以达到试验值，这可能是导致墙体侧移计算值与实测值之间差异的又一原因。

图13 连锁墙侧移实测值与计算值对比Fig.13 Comparison of measured and calculated horizontal displacements of chained wall

连锁桩弯矩计算值见图14。由图14可知，JC1位置连锁桩弯矩随着工况的变化而不断增大，开挖至坑底后基坑长时间暴露导致桩身最大负弯矩增加311.6 kN∙m，相当于工况3时桩身最大负弯矩的42.3%。显然，基坑变形的时间效应将不断消耗连锁墙设计时的安全余量。同为工况4 情况下，JC1 与JC2 位置的桩身计算弯矩亦不同，后者最大负弯矩为前者的12.2%，即越靠近基坑中部，连锁桩的最大负弯矩越大。可见，连锁桩在时空因素影响下的变形越大，对应的桩身弯矩也越大。

图14 连锁墙弯矩图Fig.14 Bending moments of chained wall

4.3 桩-桩作用影响分析

本文通过引入桩-桩界面相对位移和剪应力关系函数χ来反映连锁桩界面间的切向行为。为分析χ及界面长度D对连锁墙位移的影响设计本算例。算例中的计算模型及参数同上，χ按注浆体为M20和M30砂浆的情况考虑，切向刚度仍按第1节中的试验值取值，且区分连锁止水孔单孔和双孔注浆。

图15 为不同界面情况下连锁墙最大侧移沿基坑纵向(y向)的变化曲线，其中y=0 为基坑坑角位置。由图15可见，连锁墙侧移与其空间位置相关，表现为墙体侧移往坑角方向衰减；提高砂浆强度等级和采用双孔注浆均有助于减小墙体的整体侧移。对比注浆和不注浆的墙体侧移可见，注浆体的存在增大墙体的整体刚度，表现为坑角效应范围的增加。但需指出，采用常规砂浆材料(如本文M20 和M30 砂浆)作为连锁止水孔注浆材料，对于控制连锁墙中部最大侧移的效果有限。

图15 连锁墙纵向最大侧移对比Fig.15 Comparison of maximum horizontal displacements of chained wall in longitudinal direction

5 结论

1) 对于采用水泥砂浆作为注浆材料的连锁墙，其桩-桩界面的受力-变形发展过程可分为5 个阶段；注浆体和连锁桩之间的凹槽面破坏在先，注浆体剪切破坏在后。注浆体的选择应考虑其黏结和抗剪性能。

2) 连锁墙中桩-桩界面的切向行为可简化为理想弹-塑性模型。注浆体砂浆等级越高，界面抗剪刚度和峰值剪应力越大，但峰值剪应力对应的临界相对位移接近。

3) 提高连锁墙中桩-桩界面剪切刚度和接触长度，有利于发挥基坑变形的空间效应；但常规强度等级的砂浆注浆体对于控制连锁墙中部最大侧移的效果有限。

4) 本文方法考虑时空因素以及桩-桩相互作用对连锁墙变形的影响，适用于连锁墙时空变形分析，可为连锁墙基坑的设计优化与变形控制提供参考。